基于蒙特卡洛仿真的无人机机载LiDAR点云精度预估

刘亚萍，明 洋，王刊生，张 霄

（1.中交第二公路勘察设计研究院有限公司，湖北 武汉 430056）

激光雷达（LiDAR）是一种快速、精确获取大范围地面三维信息的测绘新技术，具有精度高、自动化程度高、数据生产周期短等优点。由于测量系统的复杂性，无人机机载LiDAR获取的激光点云精度受多因素综合影响，主要误差源包括激光测距误差、GNSS定位误差、角元素测量误差、时间误差等[1-2]，其中角元素测量误差可分为系统误差和随机误差，角元素系统误差又称安置角误差，可通过仪器检校来消除；而角元素随机误差是一种符合正态分布的偶然误差，由IMU测量精度决定，无法消除。因此，角元素误差是影响激光点云位置精度的关键因素。目前，国内外学者关于激光点云定位精度的研究，主要是根据机载Li-DAR获取点云的原理，在综合考虑扫描航高、扫描角度、安置角、坐标转换等因素的基础上，建立激光点云定位误差传播方程，再将误差传播方程线性化得到角元素随机误差与点云定位精度之间的定量评价方程[3-7]，如Dickman J[8]等利用数值仿真方法模拟平面地形进行了实验研究；王建军[9]等在此基础上增加了长方形地形和半球体地形的相关实验，定量评价了不同地形下角元素随机误差对点云定位精度的影响。然而，当前算法存在的主要缺陷为：①大多为理论公式推导，推导过程中存在较多假设，虽然许多学者对激光点云定位精度进行了理论公式推导，但往往进行了很多近似处理，不能真实反映激光点云的精度，激光扫描测量设备在获取激光点云时受诸多因素综合影响，采用理论公式不能直接回答人们所关心的激光扫描测量设备当前设备指标下所获得点云的位置误差问题；②假设各类误差之间相互独立，这与现实并不相符，为实现误差方程的线性化，一般假设各类误差之间相互独立，而实际上各误差源之间存在着复杂的联系，简单地将各误差源视为相互独立的变量，将导致定量评价结果与实际情况不符。

鉴于此，本文提出了一种基于蒙特卡洛仿真的无人机机载LiDAR点云精度预估方法，采用蒙特卡洛仿真方法，将待分析误差源（本文以角元素误差为例）引入原始测量数据中，模拟计算新的点云三维坐标，直观反映该误差源对机载激光点云坐标精度的影响。

1 研究方法

蒙特卡洛仿真是一种基于概率论和数理统计的问题求解方法，核心思想是对计算变量建立随机过程，并使其特征或参数等于该问题的解。首先对计算变量进行多次随机抽样；再将每次的抽样值代入已知的数学模型中，并求得每次抽样对应的目标变量的值；最后通过计算目标变量的统计特征（如概率分布、期望、方差等）来反映计算变量的特征[10-11]。因此，为明确无人机机载LiDAR设备的角元素随机误差与点云定位精度之间的关系，可对角元素进行多次随机抽样，通过统计点云定位精度的概率分布情况，实现对无人机机载LiDAR点云的精度预估。基于蒙特卡洛仿真的无人机机载LiDAR点云精度预估方法的基本流程如图1所示。

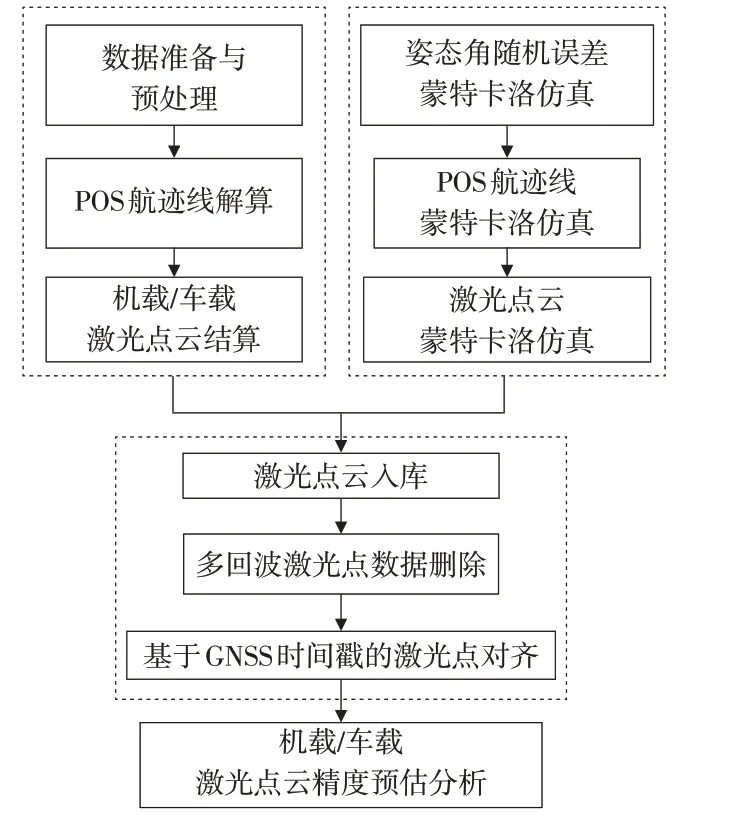
图1 基本流程图

1.1 无人机机载LiDAR点云定位模型

对于线扫描式的LiDAR设备，假设第k个激光发射点到激光脚点之间的距离向量为p k，则该激光点在WGS84坐标系中的三维空间坐标

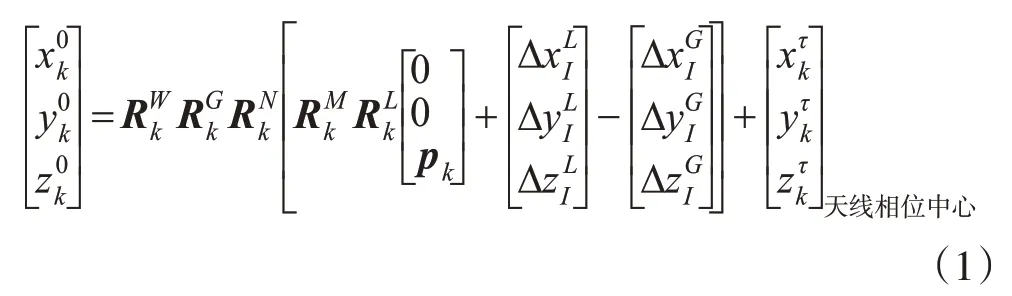
式中，( 0 ，0,p k)T为第k个激光脚点在瞬时激光束坐标系中的坐标；为第k个激光脚点从瞬时激光束坐标系到激光扫描参考坐标系的转换矩阵；为第k个激光脚点的安置误差旋转矩阵；为激光发射参考中心与惯性平台参考中心的偏移量；为天线相位中心与惯性平台参考中心的偏移量；为第k个激光脚点的姿态角旋转矩阵；为第k个激光脚点从当地水平参考坐标系到当地垂直参考坐标系的旋转矩阵；为第k个激光脚点从当地垂直参考坐标系到WGS84坐标系的旋转矩阵；为第k个激光脚点在获取瞬间GNSS测定的天线相位中心在WGS84坐标系中的坐标；k∈[1,l]；l为激光点个数。

1.2 无人机机载LiDAR点云蒙特卡洛仿真

假设无人机机载LiDAR扫描测量系统中侧滚角、俯仰角、航偏角的出厂标称精度分别为δR、δP、δH，则角元素随机误差蒙特卡洛仿真为：

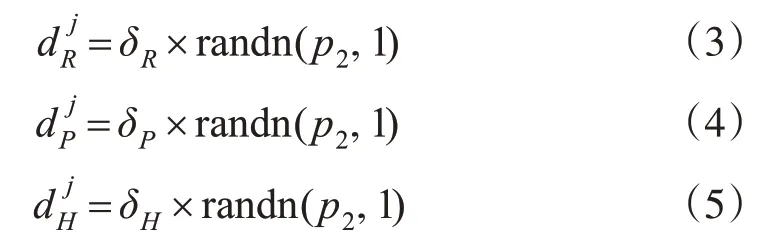
将模拟仿真的姿态角误差累加到原始航迹线文件中，得到第j组蒙特卡洛仿真的侧滚角R j、俯仰角P j和航偏角H j，即

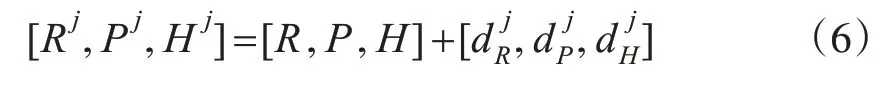
式中，R=[R1,R2,...，Rl]T；P=[P1,P2，...，Pl]T；H=[H1,H2,...，Hl]T。

将n组蒙特卡洛仿真的POS航迹线和激光测距原始数据依次代入式（1）进行激光点云解算，即可得到n组蒙特卡洛仿真的激光点云。本方法中将原始POS航迹线中的角元素值视为真值，每组蒙特卡洛仿真的POS航迹线中的角元素均引入了标称精度的角元素随机误差，因此每组蒙特卡洛仿真的激光点云坐标均可反映角元素随机误差对点云三维坐标的影响，进而实现指定角元素精度下激光点云的蒙特卡洛仿真。

1.3 无人机机载LiDAR点云精度预估

将原始激光点云和n组蒙特卡洛仿真的激光点云导入Microsoft SQL Server Management Studio数据库中，首先遍历并删除回波次数大于1的激光点，以保证激光点的时间戳信息唯一；然后将激光点云按照时间戳从小到大排序，实现原始激光点云与n组蒙特卡洛仿真激光点云的对齐。

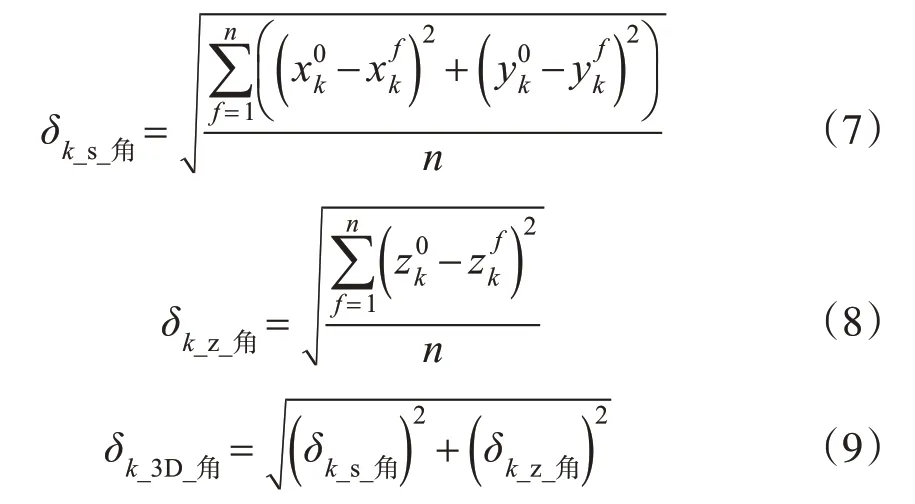
假设POS系统线元素平面精度为δs_线，高程为δz_线，则POS系统定位定姿误差对激光点坐标影响的平面中误差δk_s_pos、高程中误差δk_z_pos分别为：

假设激光点云的个数为m，则姿态角误差对整体激光点云影响的平面中误差δs_角、高程中误差δz_线为：

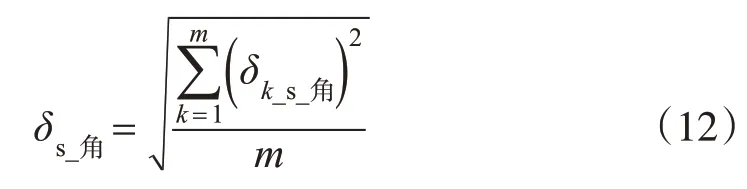
POS系统定位定姿误差对整体激光点云影响的平面中误差δs_pos、高程中误差δz_pos为：

至此，可实现激光点云位置精度的预测以及空间分布特征的分析。

2 实验数据与分析

实验数据来自广西巴马至凭祥高速公路工程机载激光测量项目，测区位于广西壮族自治区南部，呈南北走向，海拔高度在250～550 m之间；属亚热带季风气候，气候温暖，热量丰富，植被非常茂密。项目采用科卫泰KWT-X6L-15型号无人机搭载ARS-1000L线扫描式高精度LiDAR测量系统进行激光数据采集（图2），IMU采样频率设置为200 Hz，飞行航高约为300 m。

图2 无人机载三维LiDAR系统

利用采集的数据进行激光点云融合解算，获取原始激光点云的三维坐标，并将其视为“真实坐标”。ARS-1000L LiDAR测量系统的侧滚角、俯仰角、航偏角的标称精度分别为0.005°、0.005°和0.010°。为模拟POS系统角元素随机误差对机载激光点云三维坐标的影响，本文对角元素随机误差（包含侧滚角、俯仰角、航偏角三者综合作用下的误差以及三者各自作用的误差）分别进行了30次蒙特卡洛仿真。根据本文提出的方法，将角度随机误差引入原始航迹线中，得到30组蒙特卡洛仿真后的POS航迹线，再利用这些航迹线文件进行点云融合解算，最终获得30组蒙特卡洛仿真的激光点云。将原始激光点云和30组蒙特卡洛仿真激光点云依次导入Microsoft SQL Server Management Studio数据库并进行遍历操作，删除回波次数大于1的激光点并进行时标对齐，对齐后激光点个数为8 977 563。

对于单个激光点，根据式（7）～（9）可计算得到角元素随机误差对每个激光点平面、高程精度的影响，即角元素随机误差造成的激光点平面中误差δk_s_角和高程中误差δk_z_角；结合激光点的平面位置，可绘制角元素随机误差对激光点平面、高程精度影响大小的空间分布图（图3、4）；按照式（12）～（13）可计算不同角元素随机误差对测区整体激光点云平面和高程精度的影响，即平面中误差δs_角和高程中误差δz_线（表1）。结合图3和表1可知，侧滚角、俯仰角随机误差对点云平面位置精度的影响程度接近，略大于航偏角对平面位置精度的影响；航偏角随机误差对平面位置精度的影响具有明显的空间分布特征，距离航迹线越远的点，平面位置精度受航偏角随机误差的影响越大，这主要是距离放大了角度误差所致。结合图4和表1可知，侧滚角随机误差对点云高程精度的影响非常大，且具有较明显的空间分布特性，距离航迹线较近的点，高程精度受角元素误差的影响较小，可获得更高的精度；航偏角随机误差对点云高程精度的影响几乎可以忽略不计。

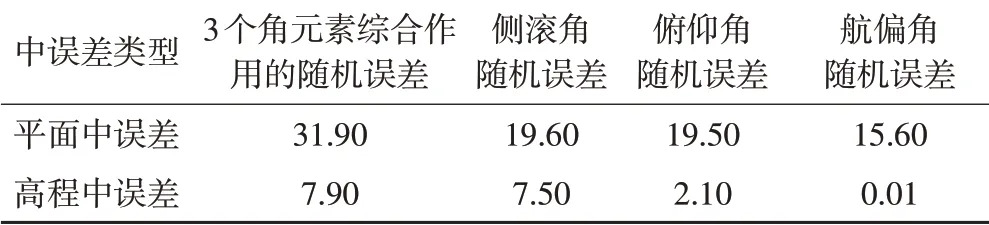
表1 角元素随机误差对整体激光点云坐标精度影响的平面、高程中误差/mm

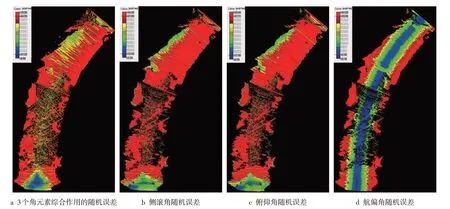
图3 角元素随机误差造成的激光点平面中误差的空间分布图

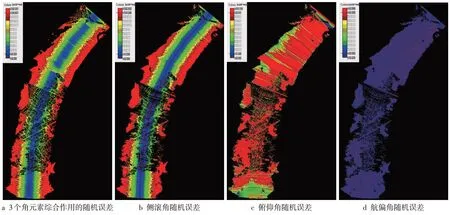
图4 角元素随机误差造成的激光点高程中误差的空间分布图

由表1可知，3个角元素误差综合作用下的激光点云平面中误差δs_角=3.19 cm、高程中误差δz_角=0.79 cm，POS系统的标称平面定位精度δs_线=1 cm、标称高程定位精度δz_线=2 cm。根据式（14）～（15）可预估POS系统的测角和定位误差对激光点云的影响，即δs_pos=3.35 cm、δz_pos=2.15 cm。至此，本文提出的基于蒙特卡洛仿真的无人机机载LiDAR点云精度预估方法，在仅考虑POS系统的测角和定位误差的基础上，激光点云整体高程精度为2.15 cm；进一步考虑目前无人机LiDAR系统的激光扫描仪测距精度为2～3 cm，则激光点云高程精度约为4.15～5.15 cm。

在本测区中，外业人员利用GPS-RTK的方式采集高程检查点554个，并利用激光点内插高程与检查点实测高程进行比较分析，得到测区激光点云的高程精度为7.3 cm。一般而言，GPS-RTK高程测量精度为5 cm，因此考虑去掉检查点自身高程误差的影响，激光点云实际高程精度约为

在实际作业过程中，无人机机载LiDAR扫描测量系统的误差来源还包括大气折射误差、数据处理误差、由于扫描电机非匀速转动而引入的扫描角误差等[12]。本实验中点云实际高程精度略大于预估的高程精度，与实际情况相符，二者精度吻合较好，验证了本文方法的有效性。无人机机载LiDAR系统的POS标称精度在设备出厂时已知，在工程实践中，可利用本文方法对无人机机载LiDAR系统获取的激光点云的三维坐标精度进行预估，再结合工程测量项目的精度要求，有针对性地进行设备选型。本文方法立足于工程应用，与实际工程需求结合紧密，避免了由设备选型不当而导致的测量成果不满足要求的情况，具有一定的社会和经济效益。

3 结语

本文提出了一种基于蒙特卡洛仿真的无人机机载LiDAR点云精度预估方法，与现有的技术相比，主要具有以下显著优点：

1）方法简单有效、结果直观、普适性强，免除了复杂的理论公式推导。利用蒙特卡洛仿真方法可对任意感兴趣的误差源进行模拟仿真，方法简单有效。对实际过程进行真实模拟，免除近似和假设条件，结果直观、可信度更高。本文方法与地形条件、激光扫描设备无关，使用范围广、方法普适性强。

2）可实现不同误差源组合影响的分析。该方法可根据需要模拟仿真不同误差源组合对激光点云三维坐标精度的影响，灵活方便，且符合控制变量的原则。

3）可分析误差源对激光点云坐标影响的空间分布特征。该方法不仅可对激光点云整体精度影响进行评估，而且可对单个激光点云的平面、高程精度影响进行分析，进而更直观有效地挖掘点云精度分布的空间特性，为航线设计、数据采集、数据处理等阶段提供理论依据。