动力电池低荷电状态风险预测

任 超

（长安大学 汽车学院，陕西 西安 710064）

随着我国大力推广新能源汽车，以及出台补贴、牌照豁免和购买税等优惠政策，我国新能源汽车数量迅速增长。到2019年6月为止，我国新能源汽车数量已达到344万辆。纯电动汽车约281万辆，占新能源汽车的81.74%。它们是新能源汽车的主要组成部分，也是本文的研究对象。但是，由于制造商在销售电动汽车时宣传的标准行驶里程与实际巡航范围相去甚远，以及汽车报警信息的不完善，导致了车主的在行驶过程中，会长时间以一个低电量行驶。电动汽车长时间低电量行驶会降低电池的寿命，加快电池的损坏。这样对动力电池是一个很大的损害，会间接造成对环境的污染。为了解决上述问题，基于国家新能源汽车大数据联盟提供的真实行车数据，本文采用基于数据的方法建立时变模型、行驶距离、电池电压、电池电流来从多个角度反映动力电池当前剩余电量荷电状态（State Of Charge, SOC）的工作状况。通过比对分析，电动汽车上应用最多的是磷酸铁锂电池，因此，本文选择磷酸铁锂电池为研究对象。

目前，动力电池SOC的估计方法可分为安培小时法、开路电压法、内阻法、线性模型法、卡尔曼滤波法，以及使用神经网络支持向量机智能算法估计动力电池的SOC[1]。李靖建立了二阶戴维南等效电路模型，通过实验数据复现出了电池的开路电压-电池的荷电状态（Open Circuit Voltage-State Of Charge, OCV-SOC）关系，结合其他估计算法，对单体磷酸铁锂电池的SOC进行了估计[2]。

上述文献主要基于在诸如实验或仿真工具的理想条件下获得的单电池的充电和放电数据来估计SOC。对车辆动力蓄电池SOC的实际运行结果估计提供的指导很少。

一些学者研究新欧洲驾驶循环周期（New European Driving Cycle, NEDC）固定模拟条件下单体电池的SOC估计，获得的估计精度是较好的，但这忽视了实际驾驶条件的复杂性和可变性，很难将研究结果应用于实践[3]。

此外，上述研究均基于单动力电池的SOC估计，对于单体电池的SOC估计在应用于整个电池组的SOC估算时无效[4]。

本文从动力电池系统整体和实际应用的角度出发，脱离理想的实验环境，根据新能源汽车国家大数据联盟采集的实车运行数据，采用大数据的分析方法。这种方法优点在于，只关注动力电池组系统的整体行为，使用主成分分析法（Principal Component Analysis, PCA），分析出来表征低SOC的特征参数。使用逻辑回归算法，总结出来动力电池低SOC时各个特征参数的规律，并用总结出来的规律对实车进行预测。使用该方法，无需对单电池的复杂非线性特性、电池组的物理结构和电化学知识等进行考虑，该算法适合于实际运行的整个电池组，充分考虑了汽车真实的行驶时各环境因素的影响。

1 算法理论依据

1.1 主成分分析

新能源汽车大数据联盟所提供的数据特征值较多，达到34个，每个特征都用来分析不现实，也会加大工作量，所以要进行数据的降维处理，筛选出相关性不高的几个特征参数进行分析。因此，选用PCA进行数据的降维处理。

PCA即主成分分析方法，是一种使用最广泛的数据降维算法。主成分分析的基本思想是在尽可能表示原特征的条件下，将原始特征经过一定的算法变化映射到低纬度空间。PCA源于通信理论的K-L变换。其问题可以描述为对于d维空间中的n个样本，考虑如何能在低维空间中更好地表示它们。

任何形式的变化在数学上都可以抽象成一个映射，或者函数。构建一个函数f(Xm×n)使得这个函数可以将矩阵Xm×n降维，矩阵Xm×n中有m个样本，每个样本有n个特征值。所以，所谓的降维，其实是减少n的数量。假设降维后的结构Zm×k，其中k＜n。那么PCA的数学表达可以表示为

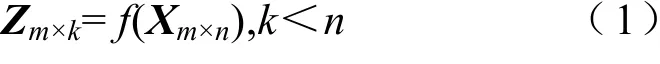
为了找到上面说的f(x)，需要做一些工作，在线性空间中，矩阵可以表示为一种映射，所以上面的问题可以转化为寻找这样一个矩阵W，该矩阵可以实现上面的映射目的：

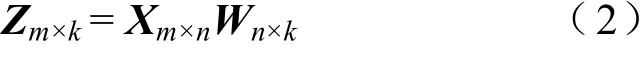
假设要把矩阵的维数降为1，也就是最后每个样本只有一个属性，即k=1。目标是使降维后的数据在那个坐标轴中的分布尽可能分散，数据分布的离散程度我们用方差来衡量。现在的目标：

最大化新坐标轴上的方差，就是让数据更加分散：

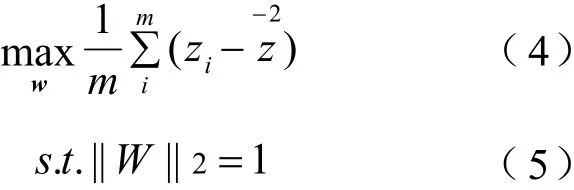
将问题转换为

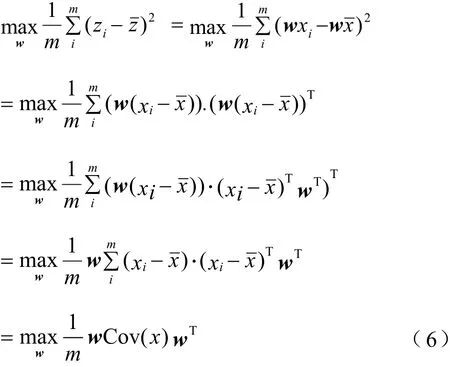
最终目标转化为

通过求解Lagrange函数，得到结果为Cov(x)ω-αω=0。

令Cov(x)ω=S，Sω-αω=0正好是特征值的定义，也就是α是矩阵S的特征值，ω是矩阵S的特征向量。但是特征值很多，ω到底是哪一个特征值。

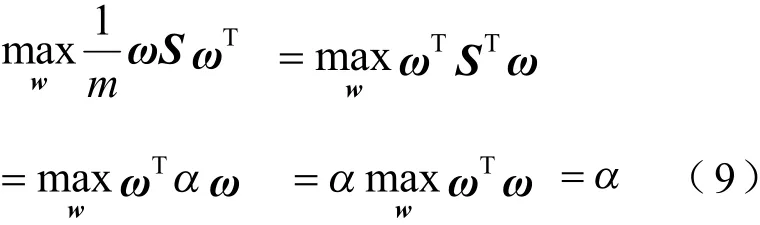
同样道理，如果是需要将数据映射为2维数据，还是求解上述的最大化方差。

原始数据包含34个特征参数，降维后的特征参数只有12个，如表1所示，极大地提高了分析的速度。

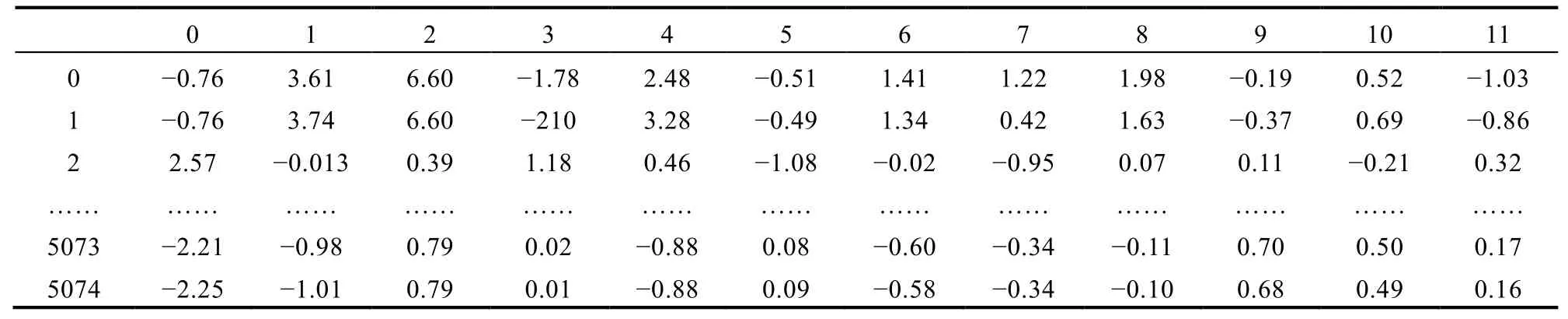
表1 降维后的特征参数

1.2 皮尔逊相关系数

皮尔逊相关也称为积差相关（或积矩相关）是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。

如果两组数据X:{X1,X2,…,Xn}和Y{Y1,Y2,…,Yn}是总体数据（例如普查结果）那么最后均值为

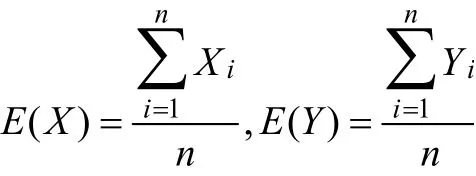
协方差：

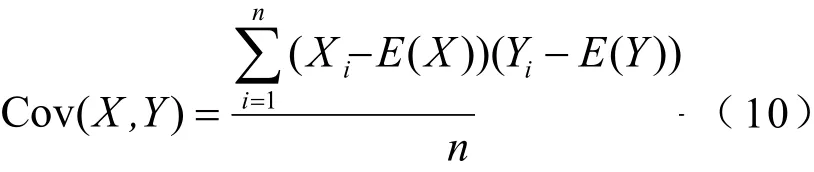
皮尔逊相关系数：

σx是X的标准差，σY是Y的标准差。观察皮尔逊相关系数的公式：我们发现皮尔逊相关系数可以看成消除了两个变量量纲影响，即将X和Y标准化后的协方差。因此，两个变量相关的程度可以使用皮尔逊相关系数来衡量。

皮尔逊相关系数在为-1到1之间波动。系数值1表示变量间呈现正相关；系数值为-1表示变量间呈现负相关。系数值为0意味着两个变量之间没有关系。

皮尔逊相关系数的使用条件是变量之间服从正态分布。因为所采集的数据量极大，所以可近似地认为变量之间的分布服从正态分布，可以使用皮尔逊相关系数进行分析。

如下所示为相关系数分析结果：系数值为0意味着两个变量之间没有关系。

0.8～1.0，极强相关；0.4～0.6，强相关；

0.2～0.4，弱相关；0.0～0.2，极弱相关。

1.3 逻辑回归算法

逻辑回归算法使用对数概率比线函数进行拟合变量间的关系[5]。如下所示：

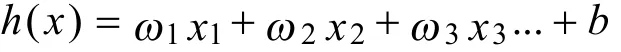
激活函数：sigmoid函数，表达式为

回归的结果输入到sigmoid函数中，最终的输出结果为[0,1]区间的一个概率值，默认0.5为阈值。

1.4 算法的步骤

步骤1：将收集到的原始数据进行清洗后，用PCA随数据的特征进行降维，以减少特征参数的个数；

步骤2；对降维后的数据再次进行皮尔逊相关系数的分析，分析出低SOC值时的影响因素，进一步达到降维的目的；

步骤3：按照8:2比例随机分开初步筛选后的数据，其中一部分作为训练集，另一部分则为测试集；

步骤4：利用逻辑回归算法，建立可以识别动力电池低SOC的模型。

2 算例及分析

为了验证和检验算法的可行性和区分效果，文中提取了低SOC报警车辆的信息，并进行了相应的特征提取。然后随机抽取数据进行实验。

单独使用逻辑回归算法对选取的数据进行求解，对报警的信息进行分类。

2.1 皮尔逊相关系数分析

通过SOC的信息已与各个特征参数之间的相关系数比较分析，选择最高电压，最低电压与电池温度作为描述电池低SOC值的特征参数。

2.2 参数分析

对报警车辆的最大电压值做散点记录，从这半年左右的数据记录中发现，电池电压最大值普遍集中在3.475 V量离群点分析在3.500 V之上。电压最小值及其于3.45 V离散点分布在众数之下。同样的，我们描述了电池最大温度与最小温度的数据分布，电池温度最大值分布比较零散，在一小段时间内变化平稳，七月后，电池温度最大值呈现线性上升趋势，而在进入秋季，九月左右出现非线性波动下降情况。

2.3 算法求解

首先需要数据归一化，将特征参量转换为无量纲的数据，然后数据按照8:2的比例分组。训练组用于算法参数的训练，数据量有5 074行；测试组用于算法的检验，数据量有1 269行。模型在训练过程的损失曲线如图2所示，可以发现，随着训练时间的延长，训练过程中的损失逐渐下降。

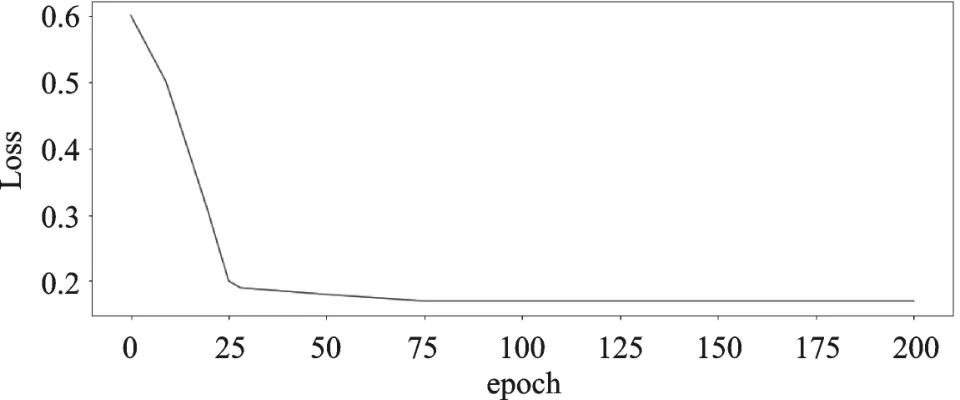
图2 Loss曲线

逻辑回归输入：

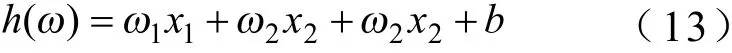
式中，x1，x2，x3分别表示最大电压值、最大温度值、最小电压值，将5 076组训练组数据输入模型中，得到模型的权重和偏置：

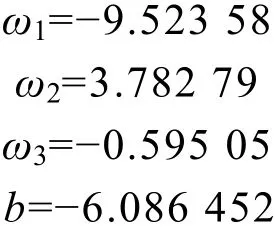
得到输入函数：

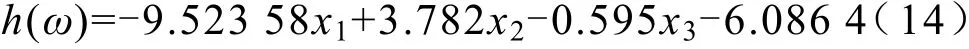
将得到的输入函数h(ω)代入到sigmoid函数g(ω)中。

若g(ω)＞0.5，输出1，表示报警；

若g(ω)＜0.5，输出0，不报警。

用训练好的模型应用在测试集上，在1 269组测试集中，有两组预测结果出错。

精确率和召回率是两个评估模型好坏的重要标准。

精确率（precision）：预测正确的个数占总的正类预测个数的比例。

召回率（recall）：真实为正例的样本中预测结果为正例的比例。

该模型的精确率和召回率分别达到了99%和99.8%高的水平，表示该模型可以应用到实际中。

3 结束语

本文基于国家新能源汽车大数据平台的大量数据，基于逻辑回归算法，对实际复杂多变工况下动力电池的运行过程进行低SOC值下的特征参数统计，并建立了模型。该模型可以用来预测汽车在真实行驶工况下是否出现低SOC的情况，并进行报警。防止汽车在行驶过程中处在一个低SOC状态行驶，对电池造成潜在的伤害。

虽然本文模型的估计结果良好，但仍存在一些局限性和需要改进的地方。对于数据质量好坏的确定没有理想的参考标准。连接到大数据联盟的汽车数量已达百万级别。汽车本身的行驶使得车内硬件质量下降将导致收集数据的误差是不可避免的事，这也是与实验室条件的差异。尽管本文进行了数据清理工作，但是原始数据的质量是模型结果准确性的根本保证。未来，作者希望通过单车行驶试验，收集高质量数据将误差控制在较小的范围内，从而克服这一问题。