基于改进AFSA 算法的大坝泄洪能力风险率仿真分析
王静波,赵 亮
(南阳市水利建筑勘测设计院,河南 南阳 473007)
0 引言
大坝泄洪闸是大坝安全的关键水利调控设施,大坝泄洪闸的泄流状态关乎水电站的整体安全,由于大坝的上下游一般高度差较大,因此水流从上游流到下游的过程具有巨大的势能,在此过程中,坝体连带其余建筑均会受到比较大的冲击力,使其出现损坏或故障,大大缩短了水利工程设施寿命。消力池能够有效改善该问题,其优化设计具有关键作用[1,2]。
现阶段,大多数的水利工程现场均安装了多种传感器以实现全面监控,通过传感器采集的数据来预测水利工程的整体运行稳定性[3]。但是随着工程的复杂性越来越高,现场监测逐渐不再适用。为此,相关专家开始对数值模拟技术进行应用。数值模拟是一种研究复杂工况的高效率手段。该技术以现场环境模拟为基础,在仿真软件中输入大坝现场参数,反演对比试验结果,为准确获取水利工程水力特性提供重要对比性参考[4]。大坝防洪风险受到多种随机性因素共同影响,因此应当归类到综合风险一类中去[5]。深入大坝防洪的领域不难发现,这些理论方法中不乏许多模拟方法,包括随机、模拟等[6,7]。涵盖了微积分方程和线性代数的种种数学理论,这些计算极限状态下随机数据的方法,对于洪峰流量的计算的确有所裨益,但评价效果却并不理想,并且概率分布也并不均匀,存在风险误差[8]。因此,防洪功能的加入能够有效提升评价结果的准确率[9]。通过随机调洪分配,将水库调洪的过程进一步进行分解,加入防洪功能的预算,得到水库水位分布特征的具体计算方法,并且计算出大坝坝体防洪功能的能力,也得到泄洪发生的概率,这就是大坝泄洪功能的风险率计算规则[10]。
1 基于改进的AFSA 算法设计大坝泄洪能力分析方法
1.1 勘测大坝坝体各项基础数据及泄洪流速
首先测绘测量大坝坝体,得到测绘图如图1。

图1 大坝坝体测绘图
如图1 所示,该大坝坝体由两部分组成,以轴线枢纽建筑为分界点,测量两侧坝体数据,使用仪器测量坝体轴线,得到坝体轴线的长度和厚度,间接计算出大坝坝体蓄水位稳定的区间。测量泄洪闸高程区间段泄流量,得到河床的平均蓄水位和顶部高程泄流量。选择平面弧形钢闸门作为泄流闸过水断面导流设施,通过测量钢闸门的面积,测量断面导流的截口。在水闸入口处监测淤沙沉积厚度,控制闸门启闭,采用液压程序测量泄洪闸的堵塞情况。对使用混凝土浇筑形成的闸墩进行厚度测量,通过闸墩的厚度计算出闸墩的体积。标高坝体墙底部,使用对比法测量坝轴线长度,得到下游坝坡坡度的比例。再测量坝身挑坎,观察是否为弧形角跌坎[11]。测量泄洪闸下游底流消力池设施的宽度和高程,观察上游洪水位发生变化的规律,测量上游洪水位延展长度。
由于消力池的表面材料为混凝土,以水为流体介质测定的渗透系数。因此,当泄洪发生时,消力池会受到较大的水流冲击力,针对该问题,优化布置消力池,有效降低其表面的受力,以增强不同频率洪水位下消力池的应用自适应性。闸底板为宽顶堰时,泄流计算公式为:

式中:δs为淹没系数,自由出流时取1.0;μ0为流量系数;e为水闸入口处监测淤沙沉积厚度;n为钢闸门的面积;b为下游坝坡坡度的比例;g为闸墩的体积。通过对大坝坝体各项基础数据进行分析,提供改进AFSA 算法计算溢洪闸调度的参考。
1.2 基于改进的AFSA 算法溢洪闸调度计算
利用勘测大坝坝体各项基础数据,以及测量计算得到的泄洪流速,改进AFSA 算法进行仿真模拟大坝泄洪,利用参数方程开展计算,计算大坝在泄洪时的溢洪闸调度:

而根据运动过程中的动量守恒,有下式:

以双参数湍流模型表述流体湍动状态,表达式为其方程:
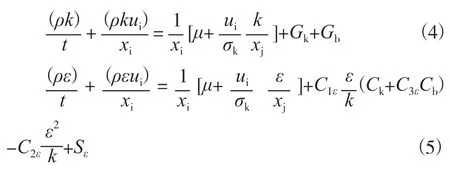
式中:ρ为压强;t为测量时间;u为流速;μ分别为静力系数;j为动力豁度系数;i为动量参数常数项;x为试验常数参数;k为流场参数;ε为效勃度系数;C流场湍动能;G为Prandtl 参数。
假定在流体运动过程中服从质量流状态,可得到溢洪闸流体的基础流速。设时刻t时的溢洪闸流体的基础流速表示为Q,该时刻的蓄水量和库水位表示为V、Z,则调洪方程表达式为:

通过计算溢洪闸调度,得到截口为t+1 实测序列的值。在历史洪水资料可获取的条件下,可考虑数据资料确定截口参数,即对截口参数利用考虑洪水的洪量与洪峰流量,计算得到大坝泄洪溢洪闸的调度,避免随机性因素影响结果,控制模拟大坝泄洪和洪水入库环境的单一性。
1.3 模拟洪水入库和泄洪的环境
在模拟洪水入库和泄洪环境的过程中,测量大坝防洪风险率和最高库水位,在判断过程中极容易受到随机性因素干扰,对出库泄洪能力分析的同时,要控制入库洪水流速这个相关变量,通过对时段洪量的测量,对洪水过程线的控制,使得测量洪峰流量和模型时产生无法避免的误差减小。计算具体的流量系数,确定下游水位与淹没流量之间的具体联系。对于调洪水位进行实时测量,将计算误差和因泥沙淤积产生的误差,整合形成误差参数,这些随机产生的因素对库水位数值产生很大的影响,确定计算的风险率特征性与调洪水位间的关联性[12,13]。建立与工程数据资料相符的数据模型,对该模型分析和选择,通过数学模型的建立,得到模拟洪水过程的曲线,利用划分坝址洪水流量,描述洪水样本,截取某段时间区间,计算该区间内的洪水流量,设原始序列为X,利用下式将其做进一步转换,即:

式中:Yt为t时段的数列集合;n为泄洪流速;Xt为基于AFSA 计算的溢洪闸调度;at为t时段的洪水样本。
对坝体水工构筑物的泄流能力进行计算,通过测算孔断面形式、围堰尺寸、流量、水头及淹没系数,得到这些数值之间的计量规律,通过复杂的淹没模型确定流量系数,以此建立全新的水工模型。设函数Q=f(x)的随机变量为X=(x1,x2,…,xn),则X=X0的一阶泰勒展开级数可表示为:


图2 洪水入库环境模拟
假设泄洪进口的流场,并根据泄洪断面的变化因子和平均变化因子,对闸门在校核洪水位、设计水位(标准水位)、死水位条件下闸门泄流能力、各个水力因素以及各个特性水位排流时尾水对坝体的作用[14]。利用工程软件对大坝枢纽施工进行了三维模型的模拟,并编制 STL 文档,然后将Flow3D 应用程序导入Flow3D;通过对坐标的加工,形成一个完整的模型。由于河流为一种随机性较强的流场,将其视为一种单一的流体,设定泄洪环境如图3。

图3 泄洪环境模拟
通过对洪水入库和泄洪环境的模拟,基于改进的AFSA 算法,得到在不同情况下各种洪水决堤的数据,从而分析大坝泄洪能力。
1.4 计算大坝泄洪能力风险率
对模拟泄洪环境得到的洪水决堤数据,以日为时间单位,录入大坝泄洪环境模拟模型,通过测量洪水在该模拟环境中的最大过程线,对各流量接口中泄洪量进行计算,并以提取标准为相关依据[15]。模拟泄洪的流体位移速度,将各流量接口的规律统一记录,将这些数据用于构建对数正态分布算法,成为改进AFSA 算法的基础,作为选取符合矢量分布规律模型的依据[16]。随机选用实测参数,将洪水参数序列排列形成10 万次以上,对比大坝承担最大洪水峰值时,模型之间的残差特性[17]。针对大坝泄洪能力,进行AFSA 算法分布在历史洪水数据整理,在形成洪水序列前调整洪水数据参数,建立统计模型并进行适当调整,计算洪水的洪峰流量,记录洪峰流量的具体特征[18,19]。因此,为了缩小入库洪水与洪水过程的差异,保留水库大坝的泄洪过程完整,选择适合生成洪水序列的调洪计算方法[20,21],完成实际泄流能力口的计算,引入修正系数,其计算公式如下:

式中:Q为实际泄洪能力;Q设为预设的泄洪能力;λ为修正系数。具有补偿性的修正系数特征呈现对称性,且红峰值普遍呈现出单峰的特性[22,23]。通过正态分布计算,可以利用AFSA 算法模型生成随机序列,计算并按三角形分布的曲线规律,总结正态分布曲线的走向,对于调洪计算的100 组数据进行整理,计算确定最高调洪水位Z。由此,以概率为基准统计洪水位,可以计算大坝泄洪决堤的情况的概率,公式为:

式中:pe为预定的基准统计洪水位;Ae为修正压力值;uv是决堤修正系数;ae为预设压力值;pv为不同情况下最高调洪水位变量[24]。通过洪水入库和泄洪的环境模拟,将计算数值带入模拟环境中验算,得到大坝泄洪决堤的水位数值,将数值带入模拟泄洪环境系统,计算出决堤水位数值在模拟大坝泄洪的随机状态中的占比,从而得到大坝泄洪能力风险率,实现改进的AFSA 算法设计大坝泄洪能力分析方法。
2 仿真实验
提出对比实验,比照所提出方法与文献[6]方法和文献[7]方法的差异,分析所获数据在数据连续性上的差异,确定更好的分析方法。
2.1 实验准备过程
通过对改进的仿真方法和文献[6]方法、文献[7]方法分别开展计算分析,利用AFSA 算法按照各个设计方案建立三维几何模型。设定算法参数包括矢量内流为N,视野为从步长为s,拥挤度因子为b,最大尝试次数为try number,最大迭代次数为T-ax,学习参数为c;计算适应度值,选出值域范围内存在的矢量内容,对内流矢量分布图进行分析。
2.2 模拟对比内流矢量的分布
根据测量得到各项参数值进行描绘内流适量分布,如图4~图6。

图4 文献[6]方法的内流矢量分布图
如图4 所示,内流矢量分布图中的白色部分代表水面线分布,黑色部分表示水气二相场的占比,文献[6]方法的内流矢量分布集中在0.4~1.2 m 之间,水面线共两条,水气二相场集中在水面线的下部,水气二相场的占比略小,水面线的面积大。
如图5 所示,文献[7]方法中的水面线主要集中在0.3~1.2 m 之间,水面线的分布明显较水气二相场的分布更广。

图5 文献[7]方法的内流矢量分布图
如图6 所示,改进的仿真方法的数值结果与模型实验结果水面线特征相同,水面线主要集中在0.6~1.2 m 之间,在模型试验中实测结果也可看出,水面线与水气二相场之间的分布更加均匀,水气二相场主要分布在0.1~0.6 m 之间,内流矢量分布更加均匀。

图6 文献[7]改进的仿真方法的内流矢量分布图
3 结束语
通过应用改进的AFSA 算法,设计大坝泄洪能力分析方法,得到更多的防洪随机性影响因素分析结果,使得仿真得到的大坝风险率精度更高。虽然获取了较好的研究成果,但在水利大坝事故风险的量化分析过程中仍需要查询和采集大量数据,且无法在短时间内实测出所有风险数据,因此在日后的研究中还需要对该问题深度探讨以达到更好的应用效果。

