水轮发电机浮动磁轭的稳定性分析探讨

梁宇强，朱忠英，孟庆钊

（东方电机有限公司，四川 德阳 618000）

0 引言

转子磁轭是发电机磁路的组成部分，同时也是磁极的固定部件。正常运行时将承受额定扭矩、磁极离心力以及自身离心力作用[1]。磁轭通过磁轭键固定到转子支架上。磁轭与转子支架之间的固定方式有两种，一种是通过径向键使磁轭与转子支架之间形成过盈配合。当转子转速增大时，磁轭随着离心力增大向外膨胀，过盈量减少，通常要求1.1～1.4倍额定转速时，磁轭与转子支架之间过盈量为0。另外一种就是磁轭与转子之间无过盈配合，即在0转速时磁轭与转子之间径向上就存在间隙，磁轭一开始就处于径向浮动状态。我们把第一种固定方式的磁轭称为非浮动磁轭，把第二种称之为浮动磁轭。相比于非浮动磁轭，浮动磁轭具有结构简单、安装周期短等诸多优点。

但是并非所有发电机都具备使用浮动磁轭的条件，因此需要对浮动磁轭的使用条件进行定量化分析。国外公司习惯通过经验公式计算一个“磁轭稳定性系数YR”来确定是否能够使用浮动磁轭；而长期以来国内电机制造厂家未对浮动磁轭的使用条件进行过专门的研究，因此目前绝大部分水轮发电机均采用非浮动磁轭。少量采用浮动磁轭的发电机，其使用依据依然采用国外公司的“磁轭稳定性系数YR”[2]。如果能定量确定浮动磁轭的使用条件，采用浮动磁轭结构无疑可以充分发挥其优点，同时也减轻设计难度。因此，本文的主要工作就是通过对浮动磁轭的稳定性分析，推导出浮动磁轭保持稳定的条件，为浮动磁轭的使用提供一个定量化的判断依据。

1 非浮动磁轭与浮动磁轭结构对比

非浮动磁轭由径向键和切向键构成，如图1、图2 所示。安装时通过加热磁轭，使磁轭膨胀到分离转速对应的磁轭膨胀量，在此条件下打入径向键，使磁轭与转子支架之间过盈配合。切向键由一个主键以及分布于主键两侧、带斜面的副键构成。在正常运行时，通过径向键作用在磁轭上的摩擦力以及切向键来承受电磁扭矩。径向键的作用还在于，它能够保证转子达到分离转速之前，磁轭始终与转子支架径向连接，这相当于增加了磁轭的径向刚度，从而减少正常运行时气隙中的磁拉力作用在磁轭上引起的椭圆变形。当转速超过分离转速时，磁轭与转子支架径向上分离，此时仅靠切向键传递扭矩。另外，由于有多个切向键在圆周上分布，相当于形成了“花键”，因此能够保证磁轭相对于转子支架同心膨胀、同心收缩。

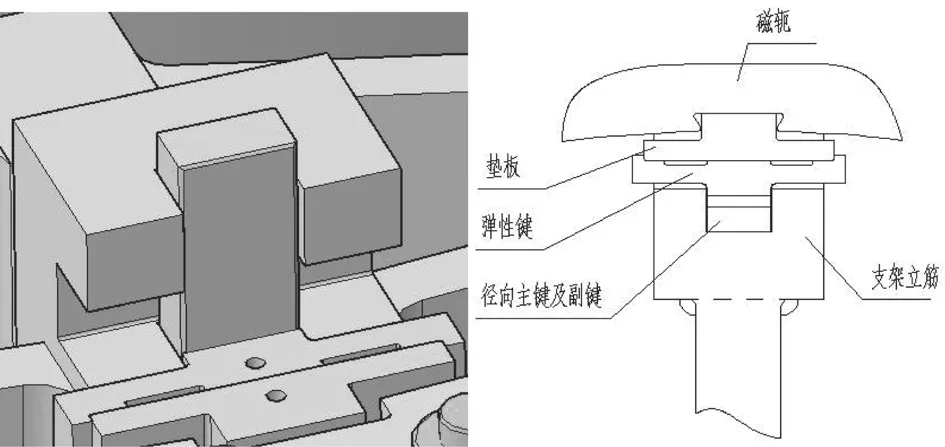
图1 磁轭径向键

图2 磁轭切向键

但是采用径向键会面临2 个问题：①转子支架需要承受过盈配合带来的巨大的径向力。该径向力在转子静止时达到最大；当机组运行时，随着磁轭受离心力向外膨胀，支架与磁轭间过盈量减少而减少。对于频繁启动的发电电动机而言，转子支架受到变幅巨大的径向力，不利于减轻转子支架疲劳，因此设计时需采用径向柔度较大的转子支架，以减少支架径向打键应力。②磁轭工地热打键前须对磁轭进行加热，为了保证磁轭加热均匀性，一方面需要严格控制温度上升速率，另一方面需要保证足够长的加热时间，这就增加了磁轭的安装周期。

浮动磁轭仅有切向键，没有径向键。转子从转动开始，磁轭便与支架径向分离，处于浮动状态，只靠圆周分布的多个切向键传递扭矩。由于不需要热打键，因此浮动磁轭的转子支架不会存在较大的打键应力，这对于提高转子支架的疲劳寿命很有好处。另外也大大地缩短了磁轭的安装周期。

图3 非浮动与浮动磁轭的固定方式

2 浮动磁轭的稳定性分析

保证磁轭的稳定性，需要满足2 个条件：

（1）保证磁轭与转轴同心，防止因磁轭偏心引起较大的轴系摆度和振动。

（2）因偏心磁拉力引起磁轭产生较大的椭圆变形应足够小，防止转子重心发生偏移、振动。

对于条件（1），前文已述及，磁轭圆周通过多个切向键固定，形成“花键”，能够保证磁轭相对于转轴同心膨胀、同心收缩。而对于条件（2），磁轭产生椭圆变形主要与2 个因素有关，①磁轭自身的机械刚度。机械刚度是阻碍磁轭变形的刚度，如果磁轭机械刚度足够大，则在外力作用下变形就越小；②气隙中的电磁刚度，该刚度是促进磁轭变形的，电磁刚度越大，磁轭变形就越大。因此讨论磁轭的稳定性需对磁轭自身的机械刚度和气隙的电磁刚度进行分析。

2.1 机械刚度

对任何机械系统进行弹性稳定性分析时，都涉及到“刚度”这一术语。在胡克定律中

式中，F—系统受到的力；K—系统机械刚度；Δx—系统边形量。

因此刚度的定义是使结构产生单位变形所需要的作用力，在国际单位中，刚度通常表示为N/mm。

转子安装时，由于定转子中心有偏差、定子铁心内径不圆、转子外径不圆等各种因素，导致定转子间气隙不均匀，运行时气隙中存在不平衡磁拉力。该力会使磁轭在径向方向产生椭圆变形。事实上要用解析法精确计算磁轭的变形量是很困难的。一方面，浮动磁轭虽然没有径向键将磁轭与支架连成整体，但是圆周上多个切向键仍然会将转子支架的一部分刚度提供给磁轭，从而提高磁轭抗变形能力，但是这个附加刚度会随着切向键的结构、数量、转子支架结构形式的不同而不同；另外一方面，磁轭的径向变形量会随着不平衡磁拉力在转子圆周上作用区域不同而不同，对于同样大的不平衡磁拉力，集中载荷比分布载荷引起的磁轭变形要大得多。

为了便于分析，我们需要将复杂的边界条件进行简化。首先忽略转子支架附加刚度的影响，将整个磁轭系统看成一个独立的圆环。其次将分布载荷的不平衡磁拉力当成集中载荷处理，则磁轭受力模型可简化为受对称径向集中载荷的圆盘或圆环模型，如图4 所示。经上述简化后，计算得到的磁轭机械刚度比实际机械刚度要小。从工程设计角度来说，按照较恶劣的情况计算得到的机械刚度来考核磁轭稳定性，这实际上也是为了留出一定的安全裕度。

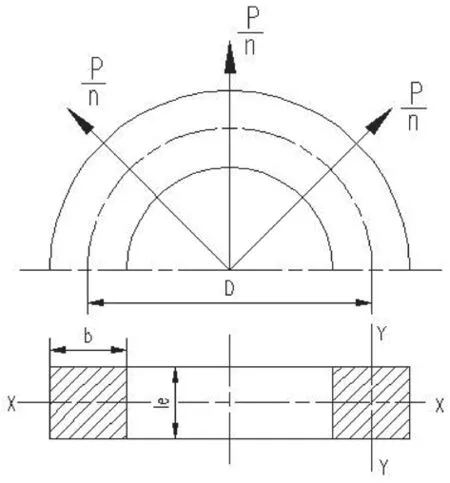
图4 磁轭机械刚度计算模型

理论上，当磁轭径向宽度b与平均直径D比值b/D＞0.1 时采用圆盘模型，当b/D＜0.1 时采用圆环模型。除了转速较高的发电机外，通常情况下，大部分磁轭b/D远小于0.1。另外，圆环模型的机械刚度显然要小于圆盘模型，因此如果圆环模型的机械刚度能够满足磁轭稳定，圆盘模型也就必然能够满足。为了使最后的分析结果更具兼容性，此处选择圆环模型。

受对称径向集中载荷的圆环中性轴所在半径的径向位移ΔxM可按式（2）计算[3]：

式中，P—集中力总和kg；n—集中力数目；D—断面重心线直径cm；le—圆环厚度cm；E—圆环弹性模量kg/cm2；J—断面对Y-Y 轴惯性矩与集中力数目n相关的系数。

按照刚度的定义，可得出磁轭机械刚度为：

按集中载荷考虑时，磁轭仅受到不平衡磁拉力和转子支架的反作用力，因此式中的n 值取2。与此对应的系数ε为1.1，将磁轭结构参数代入式（3）可得磁轭机械刚度为：

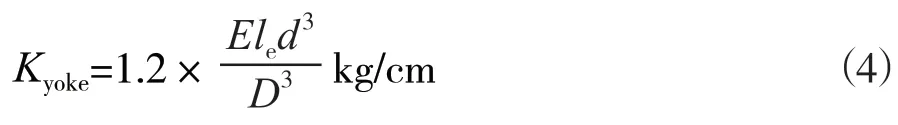
实际运行时，不平衡磁拉力不仅使磁轭椭圆变形，同时磁轭的椭圆拉伸会使定子两点的气隙减少，从而这两点上的磁拉力增加将铁心拉成椭圆。定子椭圆的长轴与磁轭椭圆的长轴成90°。

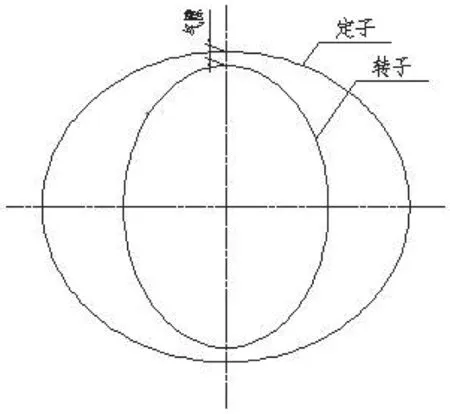
图5 定转子相对变形

由于定子椭圆和磁轭椭圆都使得气隙减少，磁拉力增加，磁轭径向变形趋势增大，等效于磁轭刚度下降了。因此可将磁轭和定子视作一对串接的弹簧，这组弹簧的等效机械刚度可以用式（5）表示：

不考虑定子机座对将定子铁心附加机械刚度的影响，同样地将定子铁心看成受对称径向集中载荷的圆环，将定子铁心结构参数近似于磁轭结构参数，则机械刚度可表示为：

式中，Er—转子磁轭弹性模量kg/cm2；Es—定子铁心弹性模量kg/cm2。

2.2 电磁刚度

若定子上有N极，转子上有S极，气隙磁密为Bd，如图6 所示，则定转子间将产生一个径向电磁力Fr。根据电工原理可知，Fr大小可按下式计算：

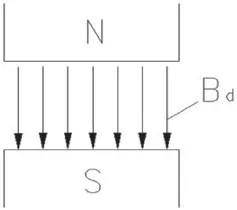
图6 N，S 极间气隙磁密分布

式中，Bd单位为Wb/m2，μ0为真空磁导率μ0=4π×10-7，算出的力单位为N/m2。实际上Bd常用单位Gs，Fr常用单位为kg/cm2，此时式（7）应该改写成

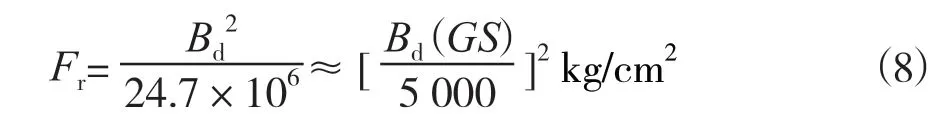
它表示在磁场作用下单位面积上受到的磁拉力。正常情况下，转子表面受到的磁拉力可表示为：

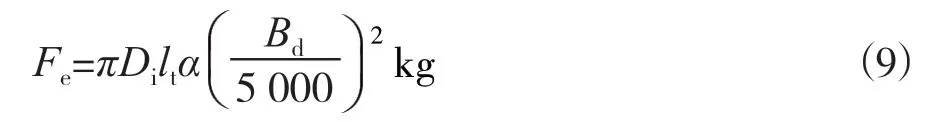
式中，Di—定子铁心内径cm，lt—定子铁心长度cm，α—极弧系数。

当存在气隙偏心时，不平衡磁拉力简化成与偏心率成正比的线性关系，表达式如下：

式中，Δδ—气隙偏心值cm，δ—气隙长度cm，β—系数，与发电机类型、磁场、槽、阻尼和绕组结构等有关，一般为0.2～0.5，本文中β取0.5。

根据刚度的定义，电磁刚度可表示为：

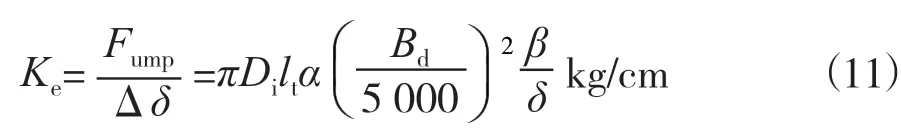
2.3 机械-电磁合成刚度作用下的磁轭稳定性

假设转子安装时，由于定转子中心不对齐，存在气隙偏心值δ1，从而存在不平衡磁拉力。在此不平衡磁拉力作用下，磁轭朝气隙偏心方向椭圆变形。磁轭变形时，存在一个随变形量线性增大的机械力，以抗拒磁轭变形，该力的方向与受到的磁拉力方向刚好相反。如果以机械抗力方向为正向，则机械抗力随变形变化、电磁力随气隙变化曲线如下：

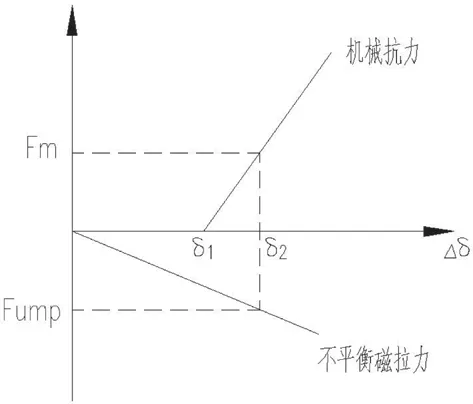
图7 机械力与电磁力随气隙偏心变化曲线

要保持磁轭稳定，必须使磁轭变形到一定程度δ2时，磁轭本身机械抗力Fm要不小于不平衡磁拉力Fump，防止磁轭进一步变形。由于：

所以，磁轭机械刚度与气隙电磁刚度应满足：

通常转子安装时，要求转子初始偏心值不大于气隙值的8%，正常运行时偏心值不大于气隙值10%，因此：

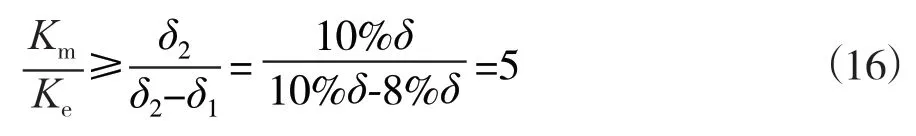
即要求磁轭机械刚度至少是气隙电磁刚度的5倍以上。将式（6）及式（11）代入式（16）可得：

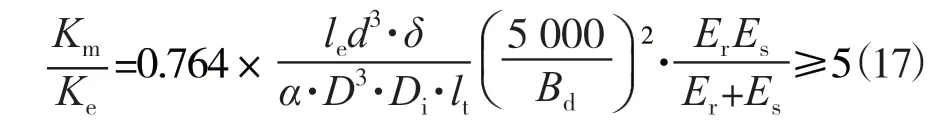
采用上式计算磁轭稳定性，关键是要确定定子铁心弹性模量Es和转子磁轭弹性模量Er。根据经验，定子铁心弹性模量一般取（1.3～1.5）×106kg/cm2。对于磁轭，如果采用叠片结构，其弹性模量可与定子铁心一致；近年来，高转速发电电动机转子磁轭普遍采用整体环板结构代替叠片结构，因此其弹性模量可近似于钢板的弹性模量，即2.1×106kg/cm2。

表1 为目前国内已经投运的、采用浮动磁轭的抽水蓄能电站的磁轭稳定性分析。从表中可见，这些电站浮动磁轭的机械刚度都远远大于电磁刚度的5 倍。

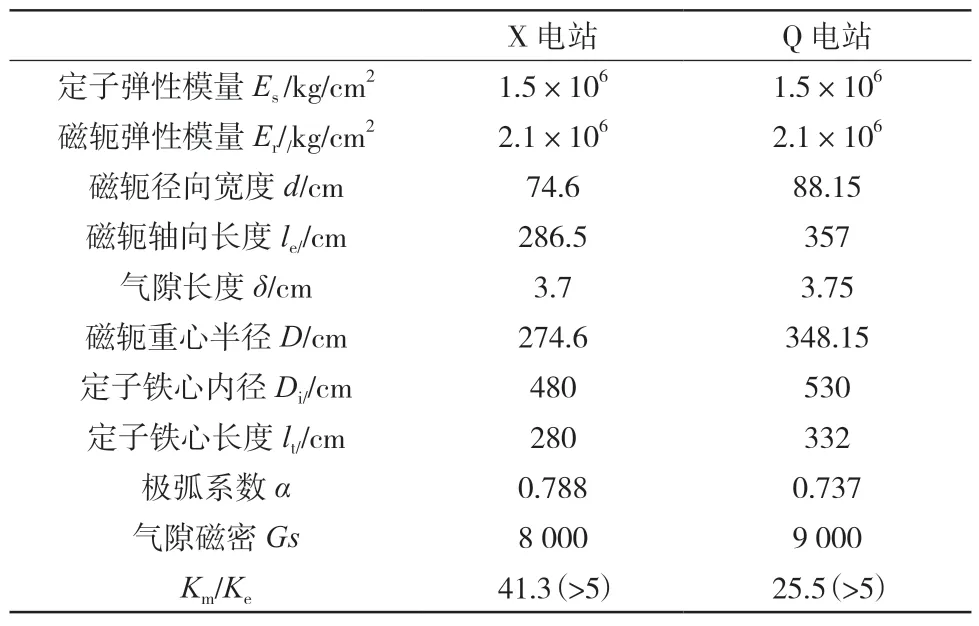
表1

3 结语

本文通过对磁轭机械刚度与气隙电磁刚度的分析，推导了浮动磁轭保持稳定性的判据及支持该判据的计算公式。该计算方法可作为浮动磁轭的选择的参考。由于对磁轭机械刚度分析时，将磁轭统一按照圆环模型处理，忽略了转子支架对磁轭附加机械刚度的影响，同时将作用在磁轭上的不平衡磁拉力按集中载荷进行考虑，因此计算出的磁轭机械刚度比实际值偏小。但是从磁轭稳定性分析角度看，上述处理方式为浮动磁轭提供了一定的安全裕度。