基于灰狼算法的多目标车间调度优化*

冯麟皓，方喜峰,2，李 俊

(1.江苏科技大学机械工程学院，镇江 212100；2.江苏省先进制造技术重点实验室，淮安 223003)

0 引言

在智能制造飞速发展的今天，车间调度问题是目前制造企业面临的一个核心问题，车间调度问题的合理解决可以有效提高制造企业的生产效率，为企业的敏捷制造提供方向。作业车间调度问题(JSP)[1]是生产调度的典型问题，在满足车间现有的生产资源前提下，以加工约束为前提，对工序进行排序以实现生产节拍的最小化，提升企业的生产和加工效率具有重要的现实意义。

为响应国家提出的“碳中和”等战略目标，我国许多的制造业将能耗问题也纳入到企业的核心优化指标，因此如何在提升车间效率的前提下，尽可能地降低能源消耗和机械负载等多个问题成为了学者研究的热门话题[2-3]。顾九春等[4]对车间的节能问题，提出了一种节能调度模型，使用并行搜索方法对总能耗和最大完工时间进行寻优，有效平衡了算法全局和局部搜索能力。张朋等[5]考虑了订单的准时交付问题，同时引入了惩罚交叉聚合函数和非支配解集，使的算法获得了良好的目标解集。NASRUDDIN等[6]采用神经网络和多目标遗传算法的方式，对热舒适和能耗这两个相互排斥的目标进行优化，算法在最大限度减少能耗的同时提高了热舒适度。ZHANG等[7]为减小车间的能源消耗，提出了一种智能调度系统，通过将零散的空闲期进行整合，对空闲期内的机器采用关闭机器的策略，有效节省了能耗。高滔等[8]对多个目标融合遗传和贪婪算法思想，两种算法对工序和机器分别寻优，证明其算法的有效性。张丽等[9]为解决车间的多目标优化问题，提出了一种融合粒子群的遗传算法，同时引入Pareto解[10-11]使解集保持多样性。

大多数学者主要聚焦于加工时间和能耗这两个目标，且传统的群优化算法或神经网络求解多目标问题时无法获取到合适的解集，导致出现目标函数数值跳动大、算法优化效果较差等问题，结合国家“智能制造”和“碳中和”的战略目标，本文从车间调度中的加工时间、机械负载、车间能耗等关键指标出发，提出了一种MSS-GWO算法，实现了减小加工时间的同时对其余关键指标的优化。

1 问题描述及模型

1.1 作业车间调度问题

作业车间的问题可描述为，一批订单中有多个不同型号的n个工件需要加工，记为{J1,J2,…,Jn}；共计m台机器，记为{M1,M2,…,Mm}；工件i的工序可用集合Oi表示，{Oi1,Oi2,…,Oij}；各工序在满足加工要求的前提下可任意选取机器，在现实的加工车间中，由于每台机器的使用频率、年限等不同，每台机器上的加工时的功率和加工时间也不尽相同，因此本文考虑以最小化最大加工时间[12]、机械负载、以及加工能耗为目标进行作业车间调度研究。

1.2 问题模型

(1)条件假设

①同一台机器同一时刻只能加工一个工件；

②同一工件的同一道工序在此时只能在一台机器上加工；

③任意工件的工序在加工开始后不能中止；

④不同工件之间不存在先后顺序；

⑤同一工件的工序之间有加工先后关系，必须在前置工序完成后才能加工；

⑥在零时刻所有工件都可开始加工。

(2)数学模型构建

MinMakespan=MaxMakespann

(1)

(2)

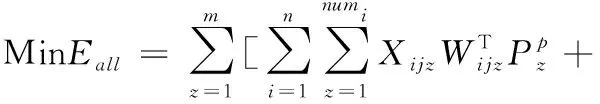
(3)

式(1)～式(3)为目标函数，式(1)表示最小完工时间以最晚结束的加工机器所对应的时间为准；式(2)表示设备的负载，为其所有机器的加工时间之和；式(3)表示该批工件加工的能源消耗。

针对以上目标函数，给出本文研究过程中的约束条件：

(4)

(3)参数定义

相关参数以含义如表1所示。

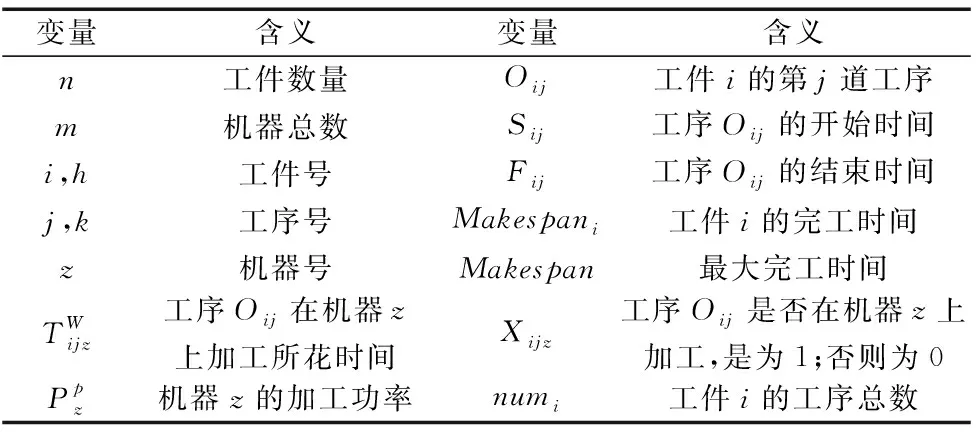
表1 相关变量及含义

2 改进灰狼算法

2.1 灰狼算法简介

灰狼算法是由MIRJALILI等[13]提出的一种模拟灰狼的社会等级制度和狩猎行为的一种启发式算法，其主要是将灰狼群按照其适应度依次分为α、β、δ、ω四类，分别由α、β、δ在狩猎过程中引导ω狼进行猎物的搜寻，从而获得最优解。

D=CXp(t)-X

(5)

X(t+1)=Xp(t)-AD

(6)

式中，

A=2ar1-a

(7)

C=2r2

(8)

式中，t为迭代次数；X(t)为当前灰狼的位置；Xp为猎物的位置；A、C分别为协同系数；r1、r2为介于[0,1]的随机数；a的数值随着迭代次数的增加线性递减，最终变为0。

在狩猎过程中，其主要依靠各具有领导能力的α、β、δ狼提供指引，ω狼向着猎物存在的方向进行搜寻，进而更新种群的位置，其数学模型如下：

(9)

(10)

(11)

式中，Xα、Xβ、Xδ分别为α、β、δ狼当前的位置；Dα、Dβ、Dδ分别为其余个体距离α、β、δ狼的距离；X为当前灰狼的位置。

2.2 改进策略

2.2.1 编码和解码

本文中的柔性作业车间数据由工序序列、加工机器序列、以及加工时间序列构成。首先，对订单中各序列进行提取，采用基于工序的ROV的升序编码方式，按照加工工序生成工序编码，其次产生[0,1]的随机数，与加工工序编码数量保持一致，依照随机数的大小进行ROV升序排列，得到了初始化的加工工序编码，如图1所示。

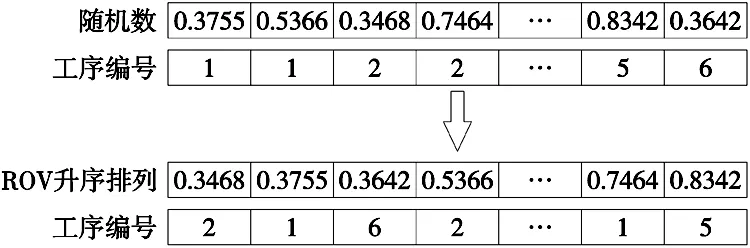
图1 工序的编码方式

工序编码中重复出现的数字表示该工件的第n道工序，通过生成的加工机器矩阵和时间矩阵能够获取该到该道工序的可选加工设备和在该设备上的加工时间。如表2所示，表中第一列中的工序编码2第一次出现，表示第2个工件的第1道工序，其可选的加工机器分别是机器3和5，所对应的加工时间分别是5和4。

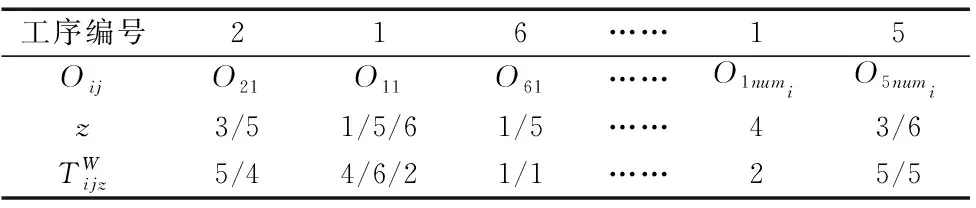
表2 工序的解码方式

2.2.2 混合交叉的搜索策略

为解决传统灰狼算法存在的无法快速收敛，算法容易陷入局部最优解的问题。提出一种混合交叉的搜索策略(mixed-cross search strategy，MSS)，引入遗传算法中的混合交叉原理，由此增加种群的多样性。该策略可以使得整个空间得到充分的搜索，同时算法在后期能够快速收敛，避免陷入局部最优解的情况。

MSS策略主要是针对3个阶段的改进，初始化种群阶段、猎物搜寻阶段、以及狼群更新阶段。

初始化种群：对于给定的搜索区域，对灰狼种群采用均匀分布的初始化方式：

(12)

式中，N为灰狼种群的初始种群个数；Xi(t)={x1,x2,x3…,xi}为迭代t次后灰狼i的位置。同时，当某一道工序对应多台加工机器时，本文引入一个选择系数Q，当随机数大于Q时，对该道工序的加工机器进行随机选择；否则选用当前工序中加工时间最大的加工机器。

猎物搜寻阶段：在原始GWO算法的猎物搜寻过程中，下一次迭代后的具体位置由α、β、δ狼的位置Xα、Xβ、Xδ决定，但仅服从α、β、δ三只领导狼的引导进行搜索，当领导狼陷入局部最优解时，狼群则会陷入局部最优解。在MSS策略中，引入遗传算法中的混合交叉原理，有效的提升了算法的搜索能力，灰狼个体搜索范围的表达式如下：

(13)

式中，Xi(t)为当前灰狼的位置坐标；Xi-GWO(t+1)为采用原始GWO算法计算出的候选灰狼的坐标。以式(13)计算出的值为半径，对邻域半径的狼群进行混合交叉处理，重新计算邻域中狼群的适应度，适应度最高的作为候选位置，其坐标表示为Xi-MSS。

狼群更新阶段：通过对比传统GWO算法生成的候选灰狼坐标Xi-GWO(t+1)以及采用MSS策略生成的灰狼坐标Xi-ISS(t+1)在种群中的适应度，将其作为最终的候选灰狼，表达式为：

(14)

算法每进行一次迭代，都会产生传统GWO以及采取MSS策略筛选出的候选灰狼，通过选出适应度高的个体，能够更好的帮助种群找到更合适的候选灰狼，以增强算法的效果。

2.2.3 非线性参数策略

在GWO算法中，当|A|>1，种群进行全局搜索；当|A|<1，种群进行局部搜索。由此可见，参数a的设置直接影响了算法搜索的性能。传统GWO算法中参数a随迭代过程由2线性减小至0，无法适应复杂的搜索过程，为此本文提出了一种非线性参数策略，该策略可以更好的对全局搜索和局部搜索进行调整，有效保持了种群的多样性。

为了能够找到最佳的函数，如图2所示，本文对非线性函数以最小化最大加工时间为目标，种群大小设置为100，选择系数Q为0.6，进行50次迭代，结果如图3所示。

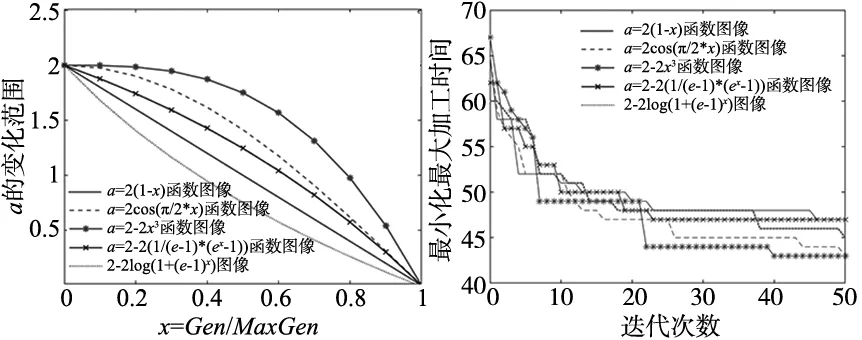
图2 参数a变换过程 图3 非线性函数对比图

通过对比可知，在初期设置参数a时，为了种群能在领导狼的引导下尽可能进行全局搜索，a取得尽可能大一些，而在算法搜索的中后期，为了使算法快速收敛，尽可能的使a的下降速度更快，最终参数a的函数可表示为：a=2-2x3。

2.2.4 动态权重搜索策略

在传统的GWO算法设置中，候选灰狼的位置仅由α狼影响，该方法会使得在α狼陷入局部最优解时降低种群的寻优能力，使算法在搜索过程中收敛缓慢，为了保证前期狼群的多样性，本文提出一种动态权重搜索策略，在前期搜索中，使得狼群受α、β、δ狼共同影响，增强种群多样性和搜索能力，防止陷入局部最优；在搜索后期，提高α狼的权重，降低β、δ狼的权重，使得算法能够快速收敛，其表达式可表示为：

X(t+1)=q1X1+q2X2+q3X3

(15)

式中，参数之间的约束关系应满足：

q1≥q2≥q3

(16)

q1+q2+q3=1

(17)

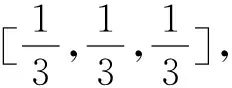
因此对q1、q2、q3分别进行了非线性函数的设计：

q1=cosμ

(18)

(19)

q3=1-q1-q2

(20)

为进一步对函数进行约束，本文引入角度μ和τ，当Gen从0到Max_Gen时，根据余弦函数和正弦函数的特性，设计了角度μ和τ的函数以保证本文中参数的变化范围。

(21)

(22)

综上所述，给出灰狼中α、β、δ狼权重q1、q2、q3在迭代过程中的变化过程，如图4所示。

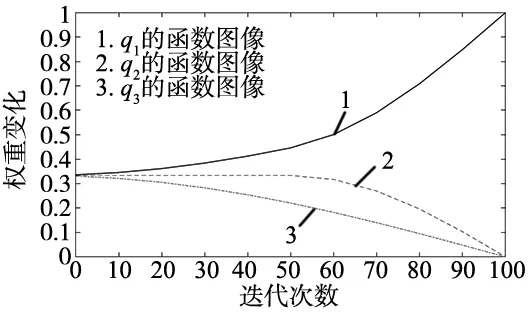
图4 权重系数的变化过程

2.3 pareto排序

对于多目标优化，常见的方法是进行加权处理和pareto解的形式，在以往大量的学者研究中，采用结合自身问题进行权重赋值，具有主观性，权重的赋值不同会对最终结果产生巨大的差异，影响最优解的准确获取。

因此本文采用pareto解集对其最大加工时间、加工及设备的负载以及能源消耗进行优化，通过外部存储保存每次迭代后的解集，通过计算非支配解集以获得最优的解。

2.4 算法流程

MSS-GWO算法的主要流程如图5所示。主要步骤为：

图5 算法流程图

步骤1：设置种群规模N，选择系数Q，迭代次数Max_Gen；

步骤2：利用随机系数Q完成种群的初始化；

步骤3：判断是否达到迭代次数，是的话跳至步骤8，否则计算初始化种群的适应度，按照其适应度进行排序，记录Pareto最优解，分别将最好的3个个体依次赋值给狼α、β、δ；

步骤4：更新当前种群的权重系数等参数；

步骤5：判断是否达到其种群规模，是则利用灰狼算法求出其候选狼，否则调制步骤3；

步骤6：根据候选狼计算出其邻域，同时对邻域内的个体进行混合交叉，筛选出新的候选狼；

步骤7：对比灰狼算法求出的候选狼与混合交叉后的候选狼，选出适应度高后候选狼更新种群，替换外部解集；

步骤8：算法结束，获得最终解集。

3 实验及结果分析

为了测试本文所提出的MSS策略的有效性，采用Python验证本文提出的算法，计算环境为CPU：5600X，内存16 G，实验验证主要包括仿真数据测试对比以及具体案例Pareto解集分析两部分组成。

3.1 数据对比

仿真测试数据来源为MK01-MK07算例[14-15]，其中包含了不同总数、不同加工机器总数、不同工序数的作业车间测试数据，同时，每台机器由于使用年限、类型不同等原因，分别对应了不同的加工功率和空载功率，如表3所示。由此使用算例对比本文提出的MSS-GWO算法、传统的GWO算法、以及文献[9]中所使用的FNSGA算法，验证本文提出算法的可行性。

表3 机器型号机器功率表

本文中算法的迭代次数为100，初始化种群数为200，随机系数Q设置为0.6。对比结果如表4所示。

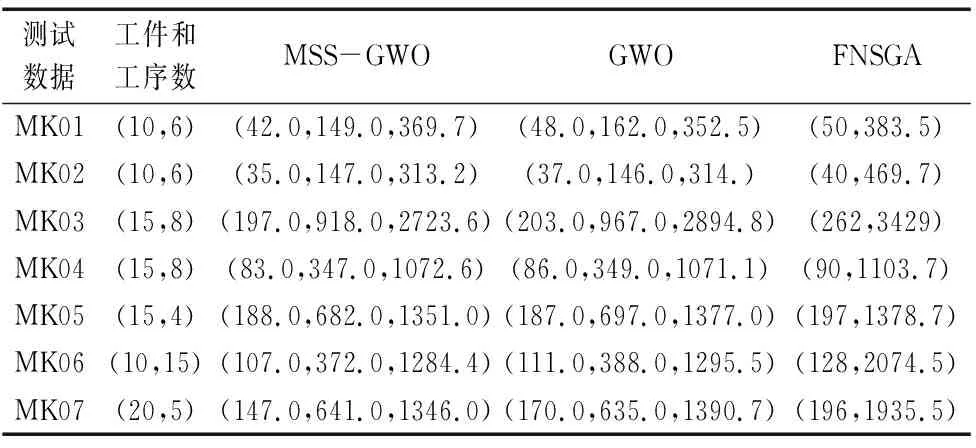
表4 算法对比表

表中(44.0,163.0,348.2)分别表示MK01算例在MSS-GWO算法得到的最小加工时间为44，机械负载为163，加工能耗为348.2，通过对其他几组算例进行算法对比可知，本文所设计的MSS-GWO算法在最小化最大加工时间、机械负载、以及加工能耗相较于文献中采用的FNSGA有较大提升，同时相较于双目标优化目标，本文进行了3个目标的优化；对比传统GWO算法，对于实际车间加工中的加工时间这一关键数据，算法保持了较优解，在实际的加工生产中可有效提高车间的效率。

3.2 Pareto解集对比

在Pareto解集方面，以MK02算例为例，对文献中的Pareto解集以及本文采用的MSS-GWO策略进行对比，绘制前沿对比图；同时对比GWO算法绘制Pareto解集，如图6和图7所示，从图中可以看出在相同的算例下，本文所设计的策略整体上保持了较优的性能，首先是获取的解集数量上更多，保持了多样性；其次在算法搜寻的最优解上，整体由于文献的解集；最后是在对于实际加工生产过程中的最小化最大加工时间均保持了较大优势，由此本文所设计的算法的搜索性能更好。

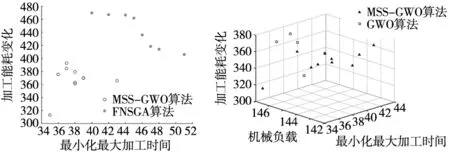
图6 两目标对比图 图7 多目标Pareto解集对比图

最后给出MK02算例的调度甘特图，如图8所示。

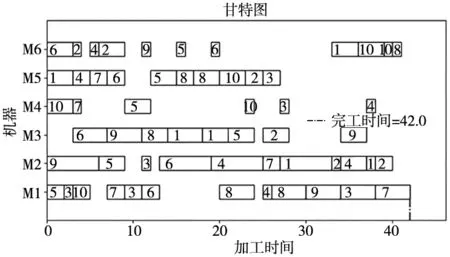
图8 MK02算例调度方案

4 结束语

为解决车间柔性调度问题，本文从考虑到车间最小化最大加工时间、机械负载、以及加工能耗等关键指标出发，构建优化目标的数学模型。同时提出了一种混合交叉原理的MSS-GWO调度策略，同时为了使算法能够获得更好的Pareto解集，进行了非线性函数的设计，最终对车间的常用的MK系列数据集进行了算法验证，实验表明本文提出的混合交叉原理的MSS-GWO策略能够较好的解决车间的多目标优化问题。

后续研究将继续紧扣车间调度问题，吸收其他算法的优点，进行车间的动态调度研究，使得车间调度问题能够得到更好的解决。