基于SSA-VMD和BiLSTM的刀具磨损状态识别*

刘子旭，刘德平

(郑州大学机械与动力工程学院，郑州 450001)

0 引言

刀具作为机床的关键部件其磨损状态对加工质量有着巨大的影响。刀具失效导致了机床高达20%的故障停机时间，并且占据了15%～40%不等的生产维护成本[1]，因此及时掌握刀具磨损状态对生产过程十分重要。

刀具的磨损和失效机理十分复杂，与工件的材料、切削三要素、使用时间、人工操作都有直接关联[2]，很难建立数学模型。而加工过程中刀具的振动信号与刀具状态有很好的关联性[3]，本文通过获取刀具加工过程中的振动信号特征，实现对刀具磨损状态的识别。

现阶段振动信号领域的分析方法主要有小波分析、经验模态分解、局部均值分解等[4]。为了更好的处理非线性非平稳信号，DRAGOMIRETSKIY等[5]提出了一种新的时频分析方法变分模态分解(VMD)。有效避免了模态混叠和噪声敏感的问题。焦博隆等[6]将VMD用于转子裂纹的检测，其降噪后频谱能充分反映信号的频率特征。陈鹏等[7]将VMD与改进阈值相结合，通过希尔伯特普分析轴承故障状态。蔡力钢等[8]利用VMD降噪并结合SVM用于刀具磨损状态的监测。但由于VMD的分解效果很大程度上取决于分解个数K和惩罚因子α的选择，因此实现VMD降噪的关键在于如何确定最优参数组合[K,α]。

降噪之后需要利用提取的特征进行模式识别。随着硬件计算速度的提升，深度学习凭借着强大的特征学习能力和可移植性在工程领域得到了广泛应用[9]。长短期记忆网络由于对时间序列信号敏感，在刀具磨损预测领域取得了不错的进展[10]。吴飞等[11]将LSTM应用到刀具磨损状态分类，取得了较高的准确率。何彦等[12]将LSTM用于刀具磨损在线监测，提高了预测精度。但LSTM只能单向训练数据序列[13]，现寻求一种同时从前后两个方向训练数据的方法。

针对上述问题，研究一种基于SSA、VMD和BiLSTM的刀具磨损状态识别模型。SSA优化VMD解决了参数选择困难的问题，将BiRNN和LSTM相结合，设计了BiLSTM模型，利用BiLSTM的学习和预测能力，对刀具磨损状态进行识别。同时采用正则化防止模型出现过拟合。实验结果表明，与传统LSTM相比该模型具有更高的准确率和稳定性。

1 理论基础

1.1 松鼠觅食算法

松鼠觅食算法(squirrel search algorithm，SSA)是一种新颖的全局仿生优化算法，具有收敛快寻优强的特点[14]。算法主要步骤如下：

步骤1：松鼠参数初始化，第i只松鼠的位置通过矢量确定，用下列矩阵表示。

(1)

FSij为第i只松鼠第j维的值，由式(2)确定。

FSij=FSiL+U(0,1)×(FSi,U-FSi,L)

(2)

式中，FSi,U和FSi,L为第j维的上界和下界。

步骤2：根据式(3)计算每只松鼠适应度值。

(3)

步骤3：计算每只松鼠位置所对应的适应值，按升序排列，依次分配到山核桃树、橡树和普通树上。

步骤4：没有天敌时松鼠移动觅食共有3种情况，按照式(4)～式(6)计算。有天敌时松鼠只在限定范围内移动。

第1种情况，松鼠从橡树向山核桃树移动。

(4)

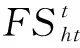
第2种情况，松鼠从普通树向橡树移动。

(5)

第3种情况，松鼠从普通树向山核桃树移动。

(6)

步骤5：根据式(7)和式(8)计算季节常量和季节变化条件。检测季节变化，防止算法陷入局部最优。

(7)

(8)

式中，t和tm分别为当前和最大迭代值；Smin的大小可以平衡全局搜索和局部搜索。如果满足季节变化条件，普通树上的松鼠位置按式(9)随机改变。

(9)

式中，Levy为列维分布。

1.2 变分模态分解

变分模态分解(variational mode decomposition，VMD)是一种自适应信号处理方法，通过迭代的方式搜寻最优变分模型，确定每个模态分解的中心频率和频带宽度[15]。将信号一次分解成多个单分量调幅调频信号。假定将原信号分解为K个分量，则对应的约束变分模型表达式如下：

(10)

式中，{uk}={u1,u2,…,uk}为K个IMF分量；{ωk}={ω1,ω2,…,ωk}为各分量的频率中心。

求取上述约束变分问题的最优解，引入如下形式的增广Lagrange函数，即：

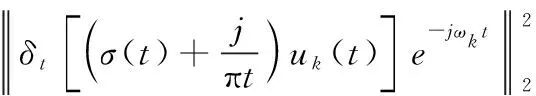
(11)

式中，α为惩罚参数；λ(t)为Lagrange乘子。

(12)

(13)

(14)

直到满足式(15)迭代停止条件，求解结束，得到K个具有限带宽的模态分量。

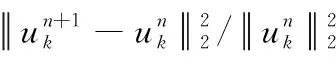
(15)

1.3 长短期记忆网络

LSTM(long short term memory)长短期记忆网络是为了解决梯度消失问题提出的一种改进的循环神经网络(RNN)，它独特的门控循环单元(GRU)很好的改善了信息的选择，提高了对信息累计速度的控制，传递信息的数据流向如图1所示。

图1 长短期记忆网络模型图

ft=σ(Wf·[ht-1,xt]+bf)

(16)

it=σ(Wi·[ht-1,xt]+bi)

(17)

ot=σ(Wa·[ht-1,xt]+ba)

(18)

(19)

(20)

ht=ot*tanh(Ct)

(21)

1.4 双向循环神经网络

Bidirectional RNN是改进的RNN模型，通过加入反向循环层使得模型可同时从前后两个方向对输入数据进行特征学习和预测，有利于掌握数据的整体信息。模型结构如图2所示。

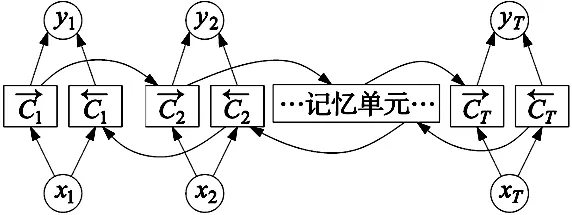
图2 双向循环神经网络模型图

正向连接从时间步1迭代到T，反向连接从时间步T迭代到1，这样在一个序列节点处能同时获得信号序列某点前后的信息，具体的计算过程如下：

(22)

(23)

(24)

2 构建刀具磨损状态识别模型

2.1 SSA优化VMD参数

VMD抗噪声干扰且具有较好的数据分解精度，但是其惩罚因子α和分解个数K的不同参数组合会对分解结果产生较大的影响。因此采用SSA对VMD的两个参数进行全局寻优，避免人为选择参数的不确定性，使信号分解达到更好的效果。

适应度函数的选择决定了SSA优化VMD参数的效果的好坏。包络熵作为一种评价信号稀疏性的标准，能够很好地反映出振动信号的不确定度。如果刀具的振动信号干扰较多，则信号有较弱的稀疏性，包络熵的值较大；如果刀具的振动信号干扰较少，则信号具有较强稀疏性，包络熵的值较小[16]。因此SSA优化VMD参数时选择包络熵作为适应度函数。图3是SSA寻优VMD参数[K,α]的流程图。

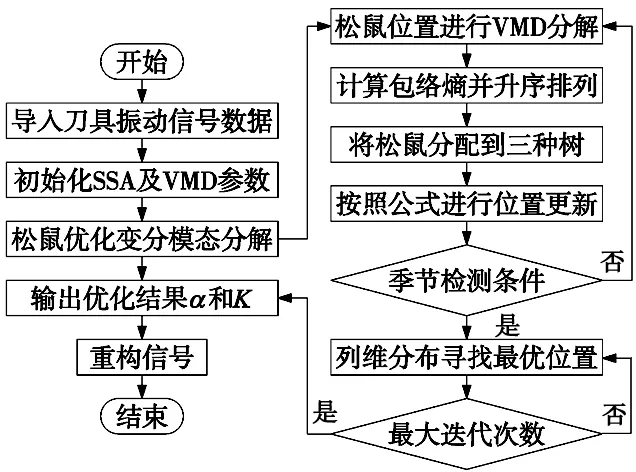
图3 SSA优化VMD参数流程图

主要步骤如下：

步骤1：设定初始参数，最优解[K,α]设为松鼠个体的位置，K和α的取值范围分别是[1,10]和[0,3000]，确定包络熵为适应度函数，种群数量取100，最大迭代次数取1000，维度为2，摩擦阻力系数CD=0.6。

步骤2：初始化种群位置，计算各个位置松鼠的适应度函数值，升序排列，按照式(4)～式(6)进行位置更新，同时计算季节检测值，若满足季节变化条件，松鼠位置按照式(9)进行更新，列维分布帮助算法更好的进行全局搜索。

步骤3：重复上述步骤直至满足最大迭代次数，优化结束，输出山核桃树上的松鼠位置作为全局最优解[K,α]。将上一步得到的[K,α]输入VMD，对信号进行分解，并对信号进行重构。

2.2 构建BiLSTM模型

双向长短期记忆网络(bidirectional long short term memory，BiLSTM)是LSTM的改进模型，同时引入前向和反向过程，使得LSTM分别从前后两个方向对信号进行处理，提高了信号的前后关联性，有利于模型学到更多的特征。模型结构示意图如图4所示。

图4 BiLSTM模型图

2.3 SSA-VMD-BiLSTM刀具磨损状态识别模型

SSA-VMD-BiLSTM刀具磨损预测模型如图5所示。

图5 刀具磨损识别模型图

刀具磨损识别的主要步骤如下：

步骤1：采集加工过程中刀具的振动信号；

步骤2：采用SSA优化VMD的参数，用VMD将振动信号分解为若干模态分量；

步骤3：将模态分量与原始信号和重构信号联合构建样本集；

步骤4：构建BiLSTM模型，输入数据训练，调整模型参数，寻找最优模型；

步骤5：输出识别结果。

3 实验验证

3.1 实验数据

实验在数控机床CAK3675V上进行，用93°外圆车刀对圆柱状材料进行车削加工，加速度传感器固定在刀具的水平和竖直方向，使用传感器采集刀具加工过程中的振动信号。通过电荷放大器和数据采集卡将信号输入到计算机中进行分析并保存。图6为具体的实验装置，表1为实验设备参数。

图6 实验装置

表1 实验设备参数

根据数控车床和材料参数设计切削加工工艺参数组合如表2所示。对两种材料做切削加工实验，共分为6组。

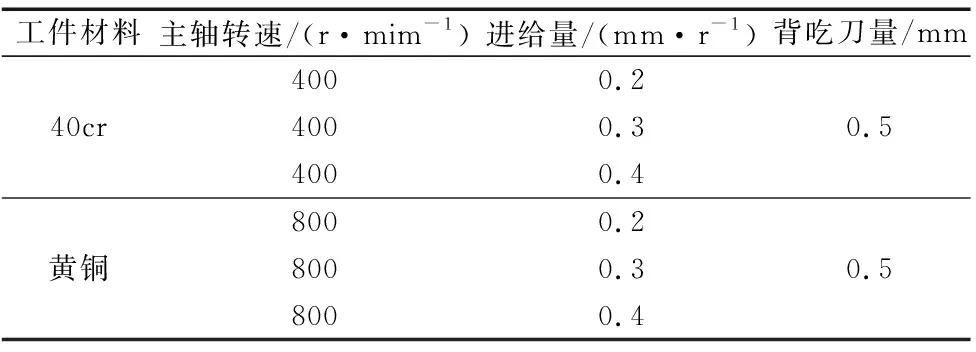
表2 实验加工参数

本实验根据ISO标准[17]最终确定当该车刀后刀面磨损值达到0.3 mm时，判定刀具磨钝。定制4种磨损状态刀具各两把，表3为具体参数，图7为实验采用的正常磨损状态的刀具图。

图7 刀具磨损图

表3 刀具磨损阶段划分 (mm)

每种刀具状态2把车刀，分别采用表2的6种加工工艺参数进行实验，每次走刀1 min，走刀2次。每种磨损状态共2×6×2=24组数据，4种状态一共得到4×24=96组实验数据。

3.2 数据处理

为了更好地对刀具磨损状态做分类，将信号进行降噪和扩充处理。首先以包络熵为适应度函数，用SSA算法优化VMD参数，参数初始值如表4所示。

表4 SSA优化VMD初始参数

SSA优化VMD之前松鼠的初始位置分布如图8左所示，经过寻优之后得到点[4,1834]如图8右所示。所以得到最优的参数组合[K,α]=[4,1834]。

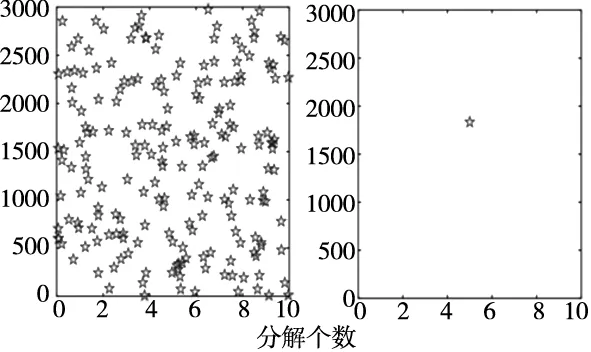
图8 粒子分布图

接着将最优参数组合代入VMD，对采集到的磨钝失效刀具振动信号进行分析，VMD分解得到信号的4组模态分量如图9所示，成功提取出信号特征。接着对分解完的信号进行重构得到降噪后的信号频域图如图10b所示。通过对比降噪前后的信号可以发现降噪后的信号频率特征更明显，说明去除了部分噪声，同时刀具振动信号的特征得以保留。

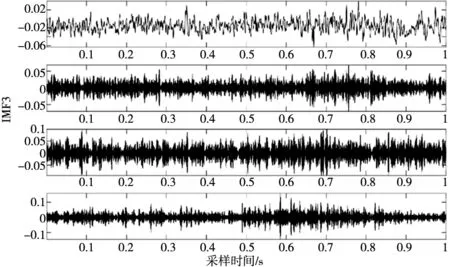
图9 IMF分量图

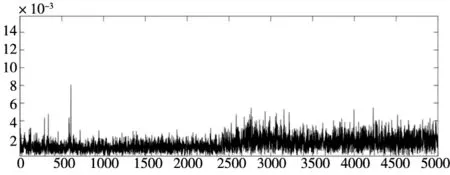
(a) 原始信号

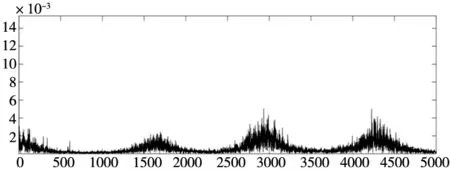
(b) 降噪信号图10 刀具信号频域图

接着将降噪前原始信号、降噪后重构信号和4组模态分量共同组成6×1原始数据集。对每一组数据不重复的取2048个点为一个数据单元，每组数据选取1000个数据单元，所以每类样本集尺度为1000×6，所以每种磨损状态共24×1000×6=144 000个数据单元，4种磨损状态的刀具振动信号均按照上述方法处理，总数据单元为4×24×1000×6=576 000个数据单元。分别打上标签，打乱所有样本并按照[0.8,0.2]的比例划分训练集、测试集，处理之后的数据集参数如表5所示。

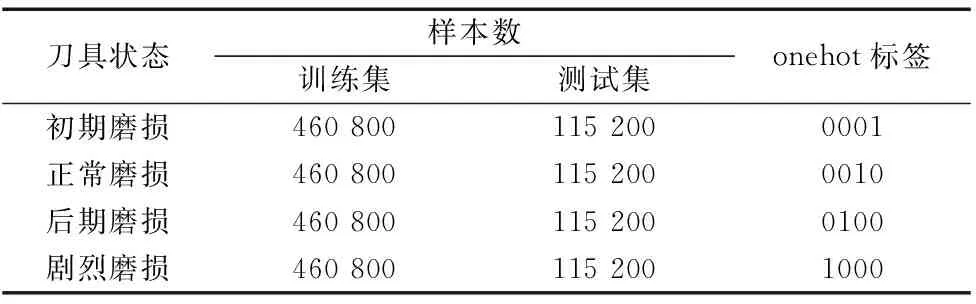
表5 数据集分组

3.3 SSA-VMD-BiLSTM刀具磨损识别模型实验

实验采用tensorflow2.0中的keras框架搭建，使用训练集训练模型，并在测试集上进行评估。BiLSTM模型主要参数如表6所示。

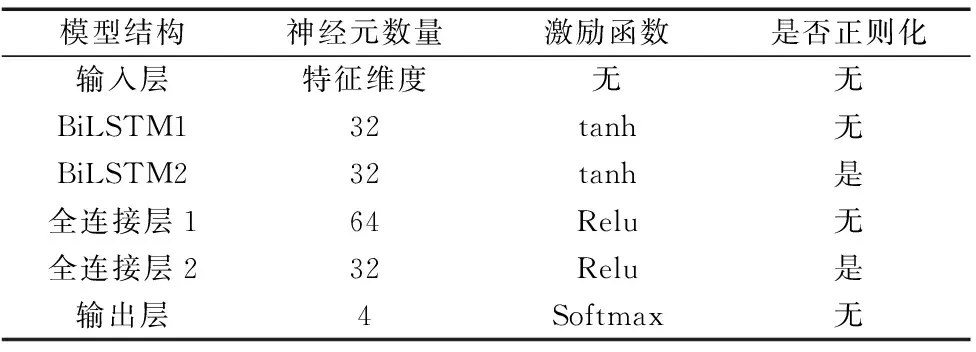
表6 BiLSTM模型主要参数

分别将原始信号与经过SSA-VMD降噪处理后的信号输入到刀具磨损识别模型当进行训练，迭代100次得到图11～图14。通过分析可以发现经过降噪处理后的信号训练损失值和准确率变化更平滑且能较快达到最优的训练效果。同时降噪后的信号在迭代40次之后损失和准确率的波动更小，模型也更加稳定。

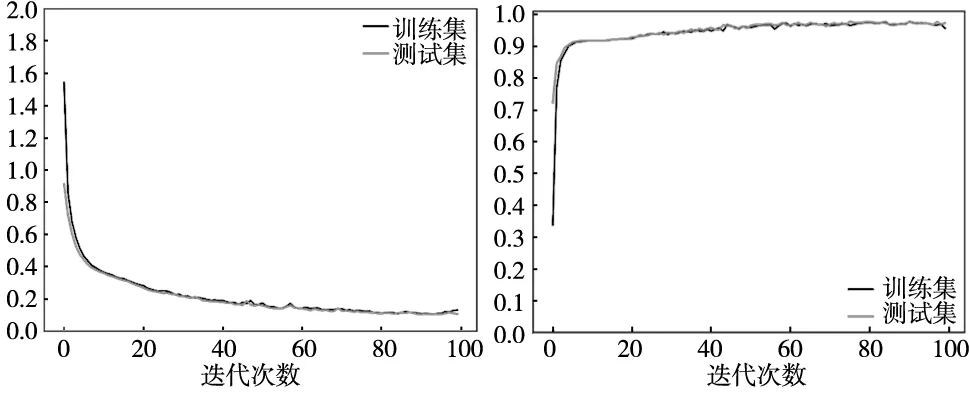
图11 降噪前信号训练损失图 图12 降噪前信号训练准确率图

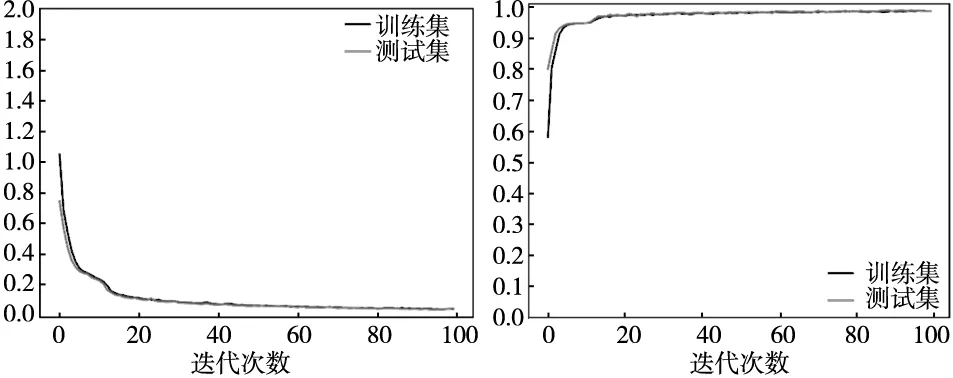
图13 降噪后信号训练损失图 图14 降噪后信号训练准确率图

进一步的将模型训练次数增加到200次，模型达到最优。用测试集测试，分别求得优化前和优化后模型的损失和准确率。经计算得降噪后信号的模型损失率降低了2.13%，准确率提高了1.64%，结果说明VMD降噪有助于刀具磨损状态识别。

3.4 识别结果与对比分析

为了进一步验证BiLSTM模型性能，与传统的LSTM模型对比。每种模型分别做10次实验，得到准确率折线图如图15所示。

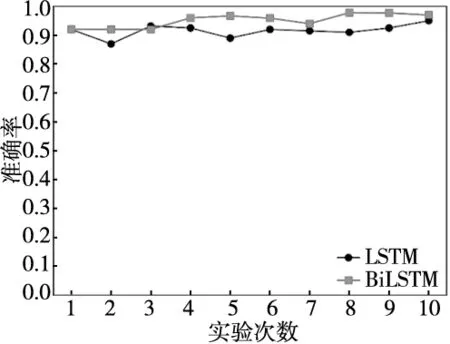
图15 准确率折线图

BiLSTM模型准确率10次中9次高于LSTM，且最高准确率也来自BiLSTM模型，因此BiLSTM更适合刀具磨损状态识别。

4 结论

本文研究了一种SSA-VMD-BiLSTM的刀具磨损状态识别模型。首先SSA优化VMD参数，利用优化后的VMD对信号进行降噪，然后构建信号特征矩阵输入到BiLSTM模型中学习，通过Softmax分类器对刀具磨损状态进行分类。得到的结论如下：

(1)SSA能很好地优化VMD超参数，提升VMD分解效果，降低信号的噪声，利用VMD算法处理振动信号具有可行性。

(2)相比传统的LSTM，BiLSTM模型能更好的处理时序信号的前后关联性，提取深层次的时序特征，提高了数控车床刀具磨损状态识别的准确率和稳定性。