双输入-单输出斜齿轮系统振动特性随非对称动力参数的演化规律

徐江海，邹冬林，张 景，塔 娜，饶柱石

（上海交通大学振动、冲击、噪声研究所机械系统与振动国家重点实验室，上海 200240）

0 引 言

非对称载荷作用下的双输入-单输出斜齿轮传动系统，以其功率密度大、结构紧凑、动力参数配比灵活等优点，成为大型舰船重要的动力推进装置中的重要结构。然而，受制于结构的特殊性，随着动力的提升，低载荷端的齿轮出现由随动耗功向主动做功的转变，意味着与之相连的齿轮副存在由背啮向正啮的状态切换，轮齿碰撞、振动、噪音等非线性失稳现象随之出现，进而影响推进系统的安全稳定运行。因此，考虑影响系统运行稳定性的多种非线性因素，建立典型的双输入-单输出斜齿轮传动系统动力学模型，研究非对称动力参数对系统振动特性影响规律，是科学解释失稳机理、抑制失稳现象发生的关键。

针对齿轮系统动力学建模，已经产生了很多研究成果。根据系统自由度数不同，先后出现了纯扭转模型、弯-扭耦合模型、弯-扭-摆耦合模型和弯-扭-摆-轴耦合模型等。上世纪80 年代，Iida 等[1]通过建立齿轮系统弯-扭耦合模型，研究了齿轮啮合的动力学特性；Kahraman[2]综合考虑了齿轮-转子在与转轴垂直的平面内两个正交方向的平移及摆动特性，建立了齿轮转子系统弯-扭-摆耦合振动模型；随着对耦合系统研究的深入，Eritenel 等[3]分别建立了齿轮弯-扭-轴-摆耦合模型，并开展动力学特性的有限元分析与试验方法研究。轮齿啮合本身所产生的内部激励和系统其它因素对轮齿啮合产生作用的外部激励，是影响系统运行稳定性的关键因素。Feng 等[4-6]通过切片法推导了斜齿轮时变啮合刚度的计算方法，并将计算结果与有限元法进行了比较；Guilbault等[7-8]研究了单自由度直齿圆柱齿轮非线性啮合阻尼，并提供了经验公式计算方法；刘占生等[9]进一步考虑弹性转轴和不平衡质量的影响，建立了齿轮、转子耦合系统动力学模型，并开展了实验研究；Ristivojević等[10]提出了基于最小弹性势能的载荷沿接触线不均匀分布的模型，得出沿作用线的时变载荷分布系数的计算公式；Gao[11]建立了考虑油膜支承刚度的双直齿轮并联驱动系统动力学模型，并研究了两个驱动齿轮啮合刚度的相位差对于振动的影响规律。在齿轮系统的动态特性随内部参数的演化规律方面，也有很多深入的研究成果。杨绍普等[12]利用增量谐波平衡法研究了直齿轮系统的非线性动力学，得出了系统参数对幅频特性的影响规律；崔亚辉等[13]通过分析内外激励下齿轮转子系统的分岔特性，研究了支承刚度、齿侧间隙对系统临界转速附近振动特性的影响规律；李以农等[14]考虑齿轮啮合力、花键联轴器啮合力和轴承非线性接触力，研究了啮合频率、滚子数目和轴承游隙等参数对齿轮-转子-轴承系统振动特性的影响规律。

虽然双输入-单输出并联斜齿轮结构广泛应用于大型舰船的动力推进系统，但对它的动力学特性的研究并不多见，在非对称动力参数下的失稳机理仍不明确。本文在考虑斜齿轮时变啮合刚度、啮合刚度相位差、非线性齿侧间隙、啮合阻尼、综合啮合误差等参数的基础上，建立双输入-单输出斜齿轮系统动力学模型，研究系统的振动特性随非对称动力参数的演化规律，阐明系统运行失稳机理。

1 双输入-单输出斜齿轮系统动力学建模

不考虑运动中转轴和轴承的影响，刚性支承的双输入-单输出斜齿轮系统物理模型和简化的扭振模型如图1所示。系统包含两个动力输入齿轮（p，q）、一个动力输出齿轮（g）和一个惯性飞轮，其中转轴1 为高载荷输入轴，转轴3 为低载荷输入轴，各齿轮通过其基圆半径（rbp，rbg和rbq）进行描述。系统中，Tp、Tg和Tq为作用于各齿轮上的力矩，θp、θg和θq为各齿轮的动态角位移，Jp和Jq为两个驱动齿轮上的转动惯量，Jf是输出轴上大齿轮和飞轮的等效转动惯量，er(t（)r=1，2）是两对齿轮副沿啮合线的时变综合传递误差，cm（rr=1，2）为两对齿轮副的平均啮合阻尼，kr(t（)r=1，2）为两对齿轮副的时变啮合刚度，D（rr=1，2）是两对齿轮副各自齿侧间隙的一半，βb为基圆螺旋角。

图1 双输入-单输出斜齿轮系统示意图Fig.1 Schematic of DI-SO helical gear system

根据牛顿第二运动定律，建立双输入-单输出斜齿轮系统纯扭转动力学方程：

2 系统参数的数学描述

2.1 时变啮合刚度

由于螺旋角的存在，斜齿轮啮合刚度不仅随着转动角位移的变化而变化，同一时刻同一啮合线不同位置的啮合刚度也不相同。利用切片法和积分思想，可将斜齿轮沿轴向划分为一系列足够小的等厚度切片，每个切片等效为直齿轮，如图2 所示。通过计算每个直齿轮切片的啮合刚度，进而积分即可得到斜齿轮单齿时变啮合刚度[15]。

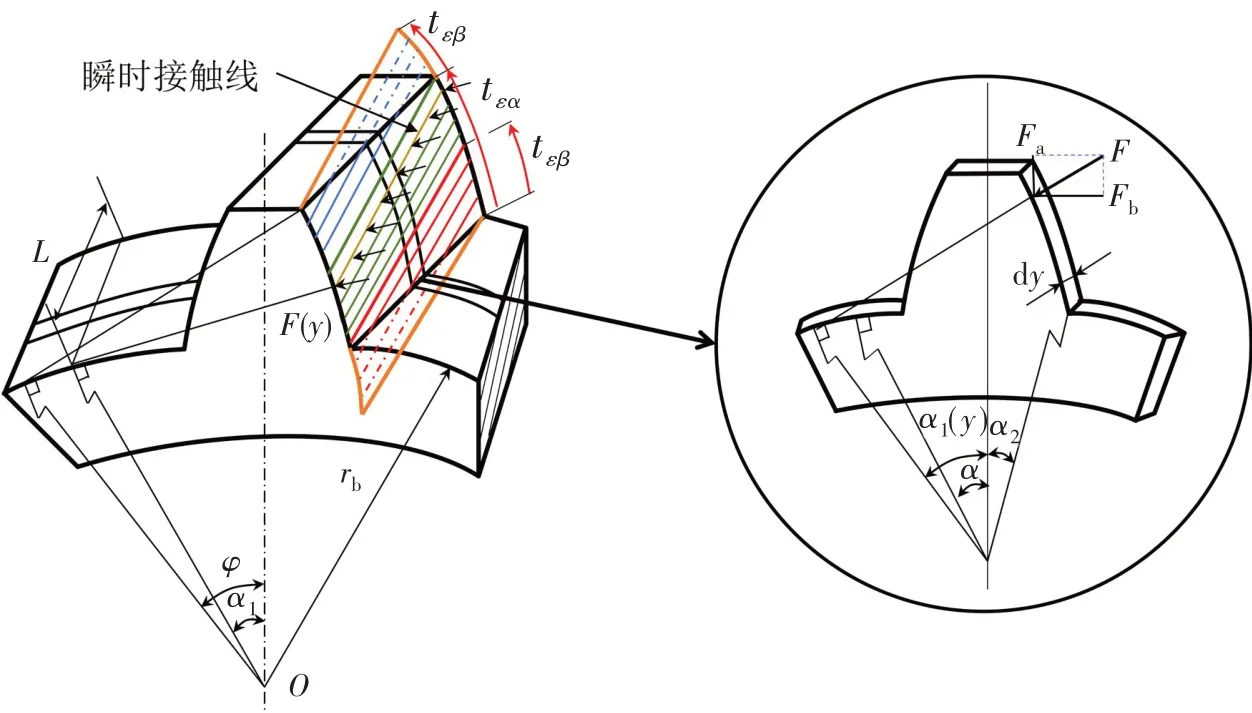
图2 斜齿轮悬臂梁模型Fig.2 Cantilever beam model of the helical gear tooth

直齿轮的时变啮合刚度由五个部分组成：弯曲刚度（kb）、剪切刚度（ks）、轴向压缩刚度（ka）、基体刚度（kf）和赫兹接触刚度（kh），各部分刚度的表达式为

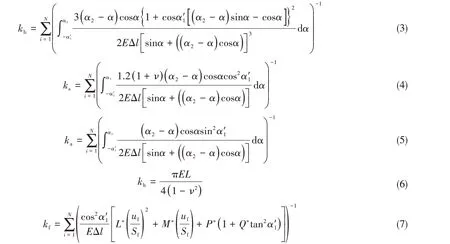
式中，N为切片沿齿宽方向的数量。将各个刚度成分按照并联方式处理，即可得到相互啮合的单齿啮合刚度为

单个轮齿从进入啮合到退出啮合的完整周期T内的啮合刚度变化过程如图3所示。

图3 单齿啮合刚度Fig.3 Meshing stiffness of one gear pair

对于总重合介于2、3之间的斜齿轮系统，在啮合过程中会出现双齿-三齿交替接触的情况。齿轮系统的综合啮合刚度是同时啮合的各个齿对共同作用的效果，其变化过程如图4所示。

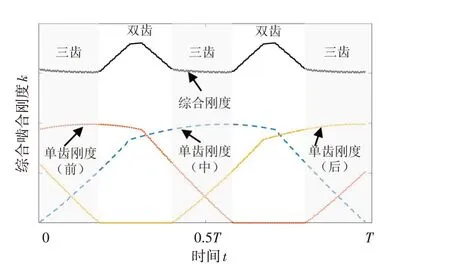
图4 综合啮合刚度Fig.4 Comprehensive meshing stiffness

将综合时变啮合刚度k(t)近似转化成三次谐波的形式：

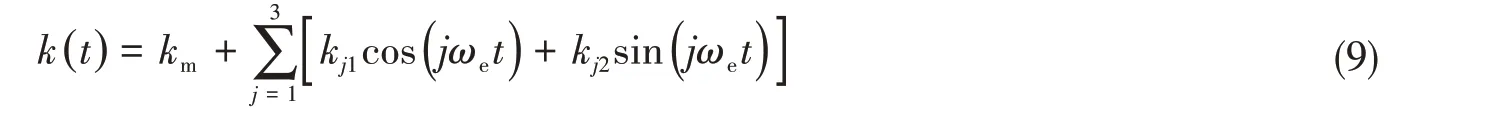
式中，km是平均啮合刚度，kj1和kj2为谐波系数，ωe为啮合频率。

2.2 啮合刚度相位差

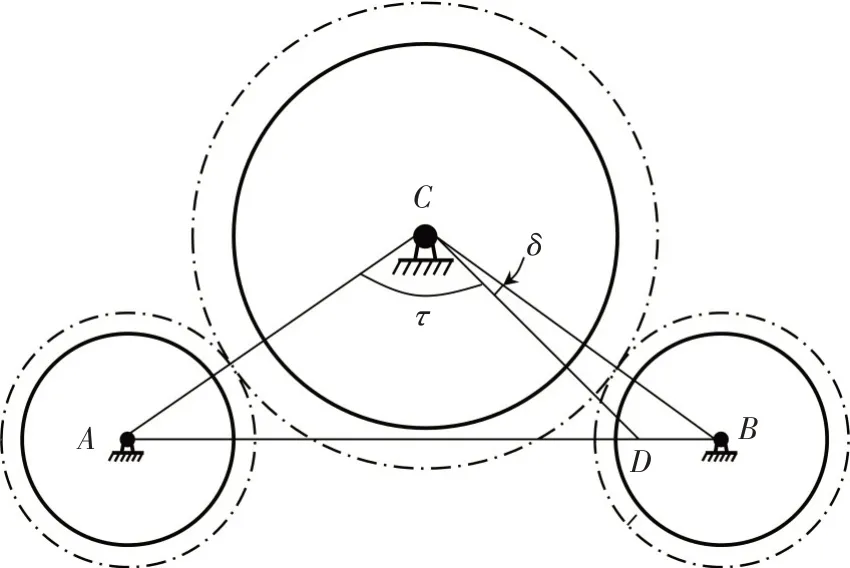
图5 齿轮布局结构Fig.5 Layout structure of the system

当∠ACB=120°，齿轮参数如表1 所示时，左右两侧啮合刚度可通过式（10）-（11）得到，刚度曲线如图6所示。

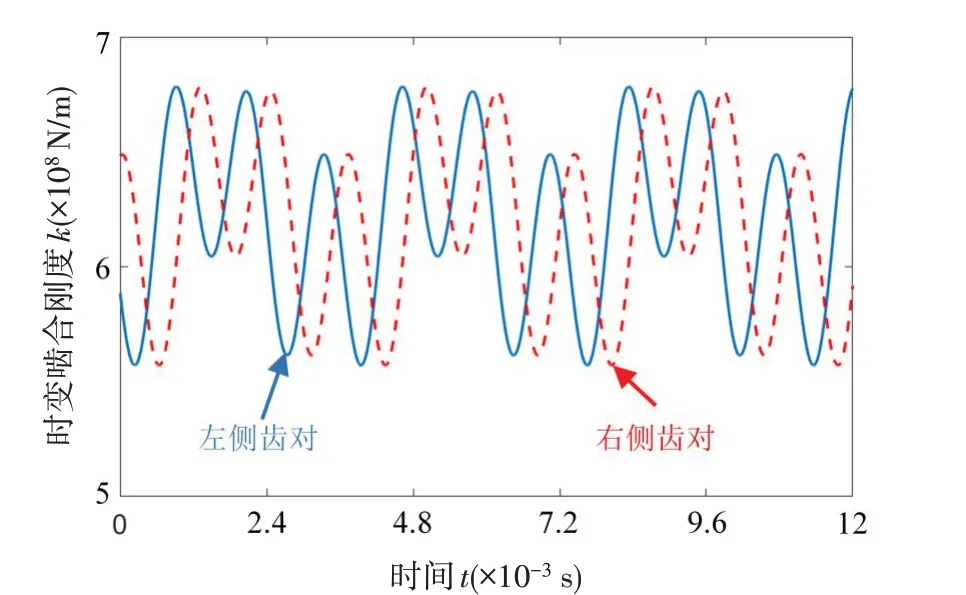
图6 左-右齿轮副时变啮合刚度Fig.6 Meshing stiffness of the left-right gear pairs

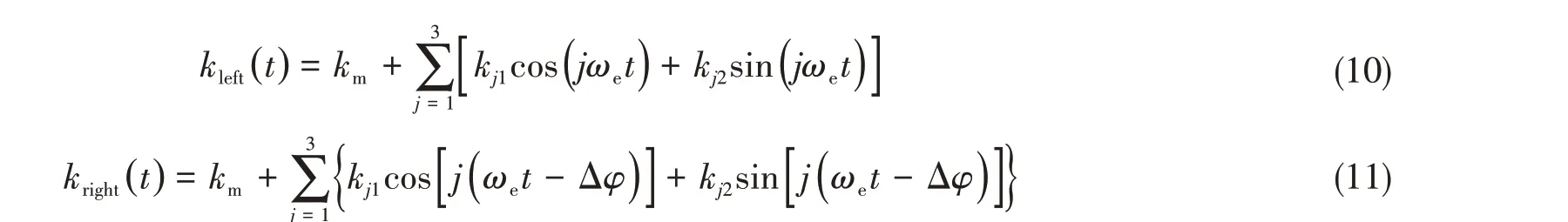
表1 斜齿轮结构参数Tab.1 Parameters of the helical gear pair

2.3 时变齿侧间隙

一般而言，斜齿轮系统的重合度大于2，其啮合过程的连续渐进渐退性使得齿轮啮入与啮出的过程比直齿轮系统更加平稳，而采用分段间隙函数g(x)，其分析结果与工程实际偏差较大，因此有必要对间隙函数g(x)进行多项式拟合。表2给出了不同阶数下多项式拟合对应的系数。

表2 不同阶数的多项式拟合系数Tab.2 Coefficients of polynomials with different orders

图7为初始分段线性函数g(x)及其各阶多项式拟合曲线。可见，随着拟合阶数的增大，偏差量逐渐减小。

图7 各阶拟合曲线Fig.7 Original piecewise curve and the fitting curves

综合考虑到计算效率和计算精度，采用7阶多项式来表示齿侧间隙函数g(x)：

3 数值分析

式（3）综合考虑了时变啮合刚度、刚度相位差、时变齿侧间隙、综合传递误差、啮合阻尼和多种啮合状态，是具有强非线性的动力学方程，因此通过解析方法难以求得其动力学特性的演化规律。通过变步长四阶-五阶Runge-Kutta 数值方法对系统动力学方程进行求解，舍弃前2000个时间序列的计算结果以排除瞬态响应的影响。

齿轮系统的结构参数如表1 所示，动力输出齿轮与飞轮的转动惯量满足Jg2/Jg1=10，阻尼比ξ=0.03，ωˉ=0.5，非对称并联输入的载荷比λ=|f2/f1|。

3.1 轻载工况f1=0.1

图8 为p、g 齿对和q、g 齿对无量纲的振动位移u和v随载荷比λ变化的分岔图。对于p、g 齿对，随着载荷比的增大，系统由拟周期运动（λ=0→0.57）进入稳定的单周期运动状态（λ=0.57→1）。与之类似，对于q、g 齿对，随着载荷比的增大，系统依次经历混沌运动状态和稳定的单周期运动状态。

图8 齿轮系统关于载荷比λ的分岔图（f1=0.1）Fig.8 Bifurcation diagrams of the gear system with the variation of parameter λ（f1=0.1）

图9～10 为系统在不同载荷比λ时，无量纲振动位移u的时频曲线、相图和Poin⁃caré 截面图。当λ为0.1 时，参数u在区间（0.7，1.3）内呈现拟单周期振动，表明p、g 齿对在正齿啮合和脱啮状态之间来回切换，其FFT 图包含明显的峰值频率0.5（基频）和小幅值振动频率1.0（二倍频）。当λ为0.8时，系统处于稳定的单周期运动状态，p、g齿对同样在正齿啮合和脱啮状态之间切换。图11-12 为系统在不同载荷比λ时，无量纲振动位移v的动力学特性。当λ为0.1 时，参数v在区间（-1.5，1.5）内振荡，表明q、g齿对在运动过程中存在正齿啮合、脱啮和背齿啮合三种运动状态，轮齿正面冲击和背面冲击交替出现。FFT图呈现具有一定宽度的离散谱。同时，其相空间轨线和Poincaré截面均表明系统为混沌运动状态。当λ为0.8时，系统进入稳定的单周期运动状态，q、g齿对在正齿啮合和脱啮状态之间切换，其FFT图包含明显的峰值频率0.5（基频）和小幅值振动频率1.0（二倍频）。

图9 λ=0.1，f1=0.1时，p、g齿对振动特性图Fig.9 Vibration characteristics of p-g gear pair(λ=0.1,f1=0.1)

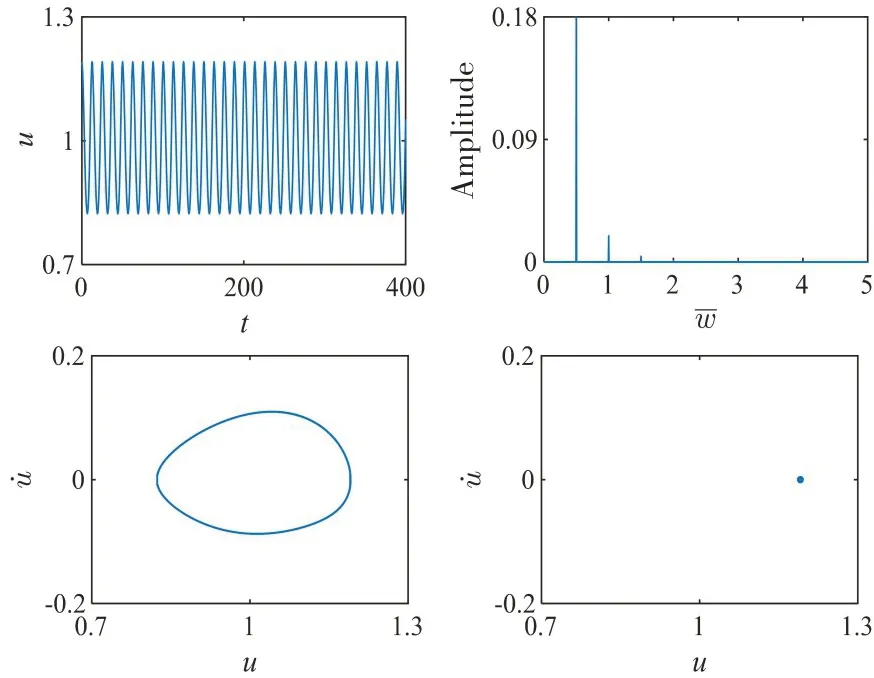
图10 λ=0.8，f1=0.1时，p、g齿对振动特性图Fig.10 Vibration characteristics of p-g gear pair(λ=0.8,f1=0.1)

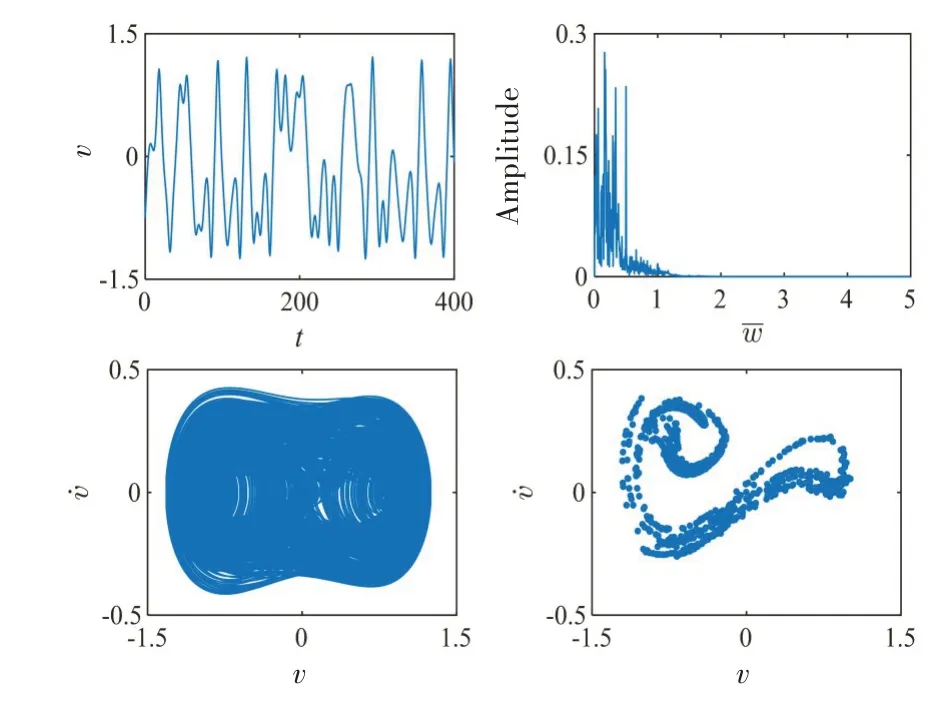
图11 λ=0.1，f1=0.1时，q、g齿对振动特性图Fig.11 Vibration characteristics of q-g gear pair(λ=0.1,f1=0.1)

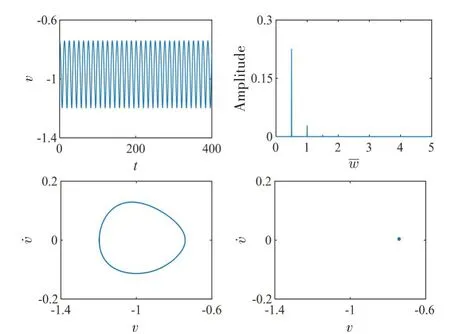
图12 λ=0.8，f1=0.1时，q、g齿对振动特性图Fig.12 Vibration characteristics of q-g gear pair(λ=0.8,f1=0.1)

3.2 重载工况f1=0.5

图13为p、g齿对和q、g齿对无量纲的振动位移u和v随载荷比λ变化的分岔图。对于p、g齿对，随着载荷比的增大，系统依次经历拟周期运动（λ=0→0.13）和稳定的三周期运动状态（λ=0.13→1）。而对于q、g齿对，随着载荷比的增大，系统表现出混沌运动状态和三周期运动状态。相对于轻载工况，重载时系统的非线性区间（混沌状态和拟周期运动状态）较窄，表明在调整系统并联输入载荷比时，重载系统更容易避开失稳区间，进入稳定的周期运动状态。

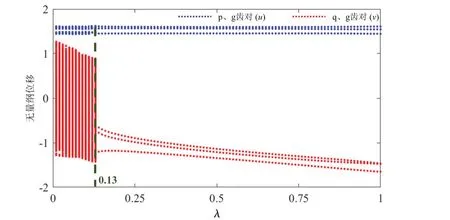
图13 齿轮系统关于载荷比λ的分岔图（f1=0.5）Fig.13 Bifurcation diagrams of the gear system with the variation of parameter λ(f1=0.5)

图14～15 为系统在不同载荷比λ时，无量纲振动位移u的动力学特性。当λ为0.1 时，参数u在区间（1.4，1.6）内振荡，表明p、g 齿对始终处于正齿啮合状态，其FFT 图包含明显的峰值频率0.5（基频）、1.0（二倍频）和1.5（三倍频），系统相图呈现多圈缠绕的封闭曲线，Poincaré截面上的点主要集中在三个点附近，此时系统近似对应三周期运动。当λ为0.8 时，参数u在区间（1.4，1.6）内呈现周期性振动，其相图和Poincaré截面表明系统呈现稳定的三周期运动状态。图16-17 为系统在不同载荷比λ时，无量纲振动位移v的动力学特性。当λ为0.1 时，参数v的动力学行为与轻载工况类似，具体表现为在区间（-1.5，1.5）内振荡，即q、g 齿对在运动过程中存在正齿啮合、脱啮和背齿啮合三种运动状态，轮齿正面冲击和背面冲击交替出现。FFT 图呈现具有一定宽度的离散谱。同时，其相空间轨线和Poincaré 截面均表明系统为混沌运动状态。当λ为0.8 时，参数v在区间（-1.6，-1.3）内周期性振动，表明q、g 齿对始终处于背齿啮合状态。啮合位移的频域信号同时出现峰值频率0.5（基频）、1.0（二倍频）和1.5（三倍频），且幅值逐步减小，其相图和Poincaré截面表明系统呈现稳定的三周期运动状态。

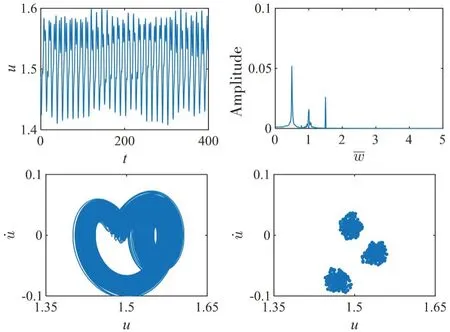
图14 λ=0.1，f1=0.5时，p、g齿对振动特性图Fig.14 Vibration characteristics of p-g gear pair(λ=0.1,f1=0.5)

图15 λ=0.8，f1=0.5时，p、g齿对振动特性图Fig.15 Vibration characteristics of p-g gear pair(λ=0.8,f1=0.5)

图16 λ=0.1，f1=0.5时，q、g齿对振动特性图Fig.16 Vibration characteristics of q-g gear pair(λ=0.1,f1=0.5)

图17 λ=0.8，f1=0.5时，q、g齿对振动特性图Fig.17 Vibration characteristics of q-g gear pair(λ=0.8,f1=0.5)

3.3 载荷值与载荷比的交叉影响

图18展示了无量纲振动位移u的最大值Max(u)和振动位移v的最小值Min(v)随载荷比λ和载荷值f1的变化趋势，表明：

图18 无量纲振动位移u和v的最值随载荷比λ的变化规律曲线Fig.18 Diagram of Max(u)and Min(v)changing with load ratio λ

（1）载荷比的变化对于高载荷输入端的p、g齿对的影响较小；而对于低载荷输入端的q、g齿对，随着载荷比λ的提高，Min(v)会存在一次稳定性突变，与前述分析对应，说明系统在该失稳临界点存在混沌运动状态与周期性运动状态的跳变。

（2）随着载荷f1的增大，高载荷输入端的Max(u)随之增大；而对于低载荷输入端，随着载荷f1的提高，失稳临界点向载荷比λ减小的方向发展。

当载荷比λ＜0.13 时，所有载荷f1工况下系统均处于混沌运动状态，此时随着载荷f1的提高，| Min(v)|逐渐增大；当0.13＜λ＜0.57 时，| Min(v)|的变化趋势与不同载荷f1通过失稳临界点的时机有关；当载荷比λ＞0.57 时，所有载荷f1工况下系统均处于周期运动状态，此时随着载荷f1的提高，|Min(v)|同样逐渐增大。

4 结 论

双输入-单输出斜齿轮传动系统是船舶动力推进装置的重要组成部分。本文基于齿轮系统内部非线性参数的数学描述，考虑了时变啮合刚度、并联输入两端的刚度激励相位差、时变齿侧间隙、啮合阻尼和综合传递误差，建立了双输入-单输出斜齿轮传动系统动力学模型，通过系统分岔图、时域和频域曲线、相图、Poincaré截面等研究了系统的动力学行为随非对称动力参数的演化规律，结果表明：

（1）随着高低并联输入两端载荷比的增大，系统的稳定性得到提高，其增强系统稳定性的效果对于低载荷输入端的齿轮副尤其明显；

（2）随着载荷值的提高，系统处于稳定的周期运动状态的载荷比区间逐渐变宽，意味着重载系统的载荷比调整范围更加宽泛；

（3）随着载荷值的提高，虽然系统稳定性得到提升，但在失稳区间内，两对齿轮副的相对振动位移幅值均随之增大，失稳振动现象更加剧烈。