基于改进人工势场法的无人船智能避障算法设计

王萍萍

（连云港职业技术学院信息工程学院，江苏连云港 222006）

无人船是一种不需要人员操纵就能够自主航行的水面或水下船舶。随着科技的不断进步和人们对自主船舶的需求日益增长，无人船的应用范围也越来越广泛。无人船可以用于多种用途，比如海洋勘探、水下考古、科学研究、海上救援、军事侦察等。在海洋勘探领域，无人船可以进行海洋地质调查、海底管道维修、石油天然气勘探等。在水下考古领域，无人船可以搭载探测设备，帮助考古人员寻找古代文明遗址。在科学研究领域，无人船可以进行海洋生物学、气象学、海洋地球物理学等方面的研究。在海上救援领域，无人船可以在危急时刻迅速前往救援现场，为落水者提供帮助。在军事侦察领域，无人船可以进行情报收集、海上监视、反潜侦察等任务。无人船的优点包括降低成本、提高效率、降低风险、减少人员伤亡等等[1]。

无人船作为一种智能航行器，要具有在复杂水文环境中进行自主航线作业的功能，主要依赖于船舶自主控制技术，其中对于其避障策略的设计是关键一环。无人船在航行时不可避免地会遭遇障碍物，例如船只、岛屿、礁石等，因此设计一种可靠的避障策略对于提高无人船的航行安全性至关重要。针对这一问题，学术界开展了大量研究，文献[2]提出了一种基于离线马尔科夫决策过程（MDP）的欠驱动AUV 的实时避碰方法，该方法将仅考虑障碍物几何特性的粗规划与AUV 运动学和动力学特性相结合，从而解决了当障碍物环境发生变化时，在重规划过程中求解MDP产生的计算量过大的问题。在机器人运动规划领域，由文献[3]提出的人工势场法是一种经典的算法，部分研究者也将其应用于解决无人海洋航行器的避障问题。文献[4]提出了一种巡航船混合路径规划算法，使用A*算法规划全局路径，在未知的水面区域利用人工势场进行局部路径规划。文献[5]提出一种考虑时间优化的改进蚁群算法，改变信息素更新方式，将该算法应用于无人救生船航迹优化，从而有效降低航行时间。文献[6]针对传统A*算法所规划的路径在避开障碍物之后无法快速回到预设航线上的问题，提出了一种改进的A*算法，该算法能够使无人航道测量船在避开障碍物之后更快地回到预设航线。文献[7]基于D*lite 算法开发了一种USV 路径规划算法，并结合人工势场法增强规划路径的安全性。文献[8]提出基于改进型DWA 的移动机器人避障路径规划，定义了关键航迹点的概念。

上述国内外文献为无人船避障算法的研究提供了诸多参考，但是大部分文献的研究都侧重于路径规划层面，即利用全局的环境信息和障碍物信息，通过一定的寻优算法得到一条最优路径，再通过一定途径实现无人船对最优路径的跟踪。这种策略的优点在于通过合理的算法设计，能够找出一条全局最优路径，但其缺点在于需要经过规划路径—跟踪路径两步才能实现完整的避障功能，如果规划的路径与无人船的动力学特性不符合，那么无人船将很难实现对规划路径的跟踪。

针对上述问题，本文基于人工势场法设计无人船的智能避障算法。首先基于牛顿欧拉法建立无人船的运动模型，然后结合得到的运动模型，基于人工势场法设计无人船的避障算法，并且针对人工势场法中的局部极小值问题提出改进措施，得到改进的人工势场法。该算法是一种端到端的避障策略，通过识别无人船周围的障碍物信息，能够直接输出执行器的控制指令，再通过无人船对控制指令的反馈信息调整执行器的控制指令，形成完整的控制回路。因此，本文提出的无人船智能避障算法是一种实时避障算法，能够充分考虑无人船的运动特性，在可达性方面具备一定的优势。

1 无人船运动模型与控制器设计

为了模拟无人船在海洋环境中的运动，首先需要建立反映无人船运动学与动力学特性的数学模型。与艏摇运动相比，无人船的横荡和纵荡运动幅度较小，因此可忽略这两个自由度的运动，从而建立无人船运动的四自由度模型。

根据文献[9]15-56，基于牛顿-欧拉法建立的无人船运动的动力学方程可以表示为

式中，V=[vxvyvzφ˙]T为无人船运动的相对速度向量，其中φ为无人船的航向角；M 为刚体惯性矩阵；C 为科氏向心力系数矩阵；D 为阻尼矩阵；G 为重力/浮力矩阵；T 和Fruddte分别为无人船受到的推进器推力和舵摆力，分别用于提供无人船动力及控制无人船航向；Fwave为无人船受到的波浪作用力。

刚体惯性矩阵可以表示为

式中，（xg,yg）表示船体坐标系原点与船体质心之间的纵向、横向距离。由于本文研究的无人船为轴对称结构，因此yg=0。

科氏向心力系数矩阵可以表示为

阻尼矩阵D 可以表示为

式中，D11、D22、D33、D44分别表示无人船平面运动和艏摇运动的阻尼系数，D（iji≠j）表示交叉阻尼系数。无人船运动的运动学方程可以表示为

式中，[x y zφ]T为无人船运动的位置与姿态向量，T 为船体坐标系向惯性坐标系转换的转换矩阵，可表示为

为了对无人船的航向进行控制，本文设计基于PD 控制器的航向控制算法。记无人船航向与预设航向之间的偏差为

将△φ作为PD 控制器的控制输入，则输出舵机舵摆角度为

式中，Kp、Kd分别为关于比例和导数的增益。△φ˙为航向偏差的变化率。

基于PD 控制器的无人船航向控制流程见图1。

图1 PD 航向控制流程

基于上述建模思路，使用Simulink 仿真软件搭建无人船运动仿真程序。通过为无人船施加预设航向的阶跃输入信号，验证该PD 航向控制器的有效性，输入信号与无人船的航向响应见图2。从图2 可以看出，无人船很好地完成了对阶跃输入的跟踪，说明所设计的PD 控制器能够完成对无人船的航向控制，所建立的无人船运动控制模型可以用于对其避障算法的研究。

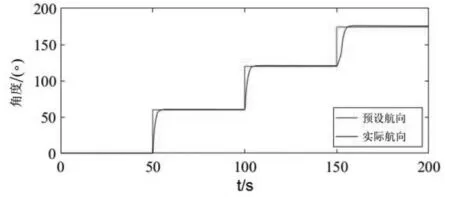
图2 无人船对预设航向阶跃信号的航向响应

2 无人船避障算法设计与验证

2.1 人工势场法

基于上节构建的无人船运动模型与控制器，本节基于人工势场法设计无人船的避障算法。人工势场法是一种经典的机器人路径规划算法，基本原理见图3所示。它模拟了物理世界中的势场理论，将机器人和障碍物看作点电荷，通过对机器人施加势场和障碍物施加反向的斥力场来实现机器人的自主避障和路径规划。在人工势场法中，机器人被看作一个自由粒子，在其周围施加一个目标势场和障碍物施加的斥力场。目标势场使机器人朝向目标点移动，而斥力场则使机器人避开障碍物。这种势场模拟的方法具有简单、高效、易于实现等优点，适用于小型机器人的路径规划和避障。

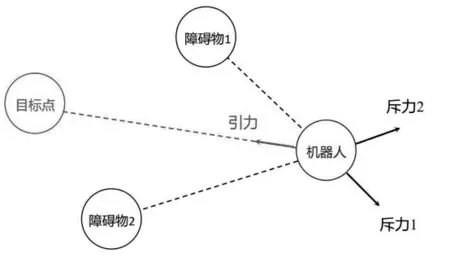
图3 人工势场法原理

机器人在工作空间内的任一点都会受到虚拟引力势场的作用，引力势的大小与机器人距目标点的距离有关。该距离越大，引力势越大，目标点对机器人的吸引力越强；反之，该距离越小，引力势越小，目标点对机器人的吸引力越小。当机器人到达目标点时，引力势为零，即不再受到目标点的引力作用。由此可知引力势函数可定义为

式中，（x,y）为机器人的位置坐标；k1为引力势函数的增益系数；L1为机器人距目标点的距离。

当机器人进入障碍物的影响范围内时，才会受到斥力势的作用。距离障碍物越近，斥力势越大，障碍物对机器人的排斥力越大；距离障碍物越远，斥力势越小，障碍物对机器人的排斥力越小。因此，斥力势可定义为

式中，k2为斥力势函数的增益系数；L0为障碍物的影响距离，L2为机器人与障碍物之间的距离。

图4 展示了引力场和斥力场叠加后的总势场示意图。为了达到势能最小的目标点处，机器人通过搜索势能减小的方式进行路径规划，从而绕开障碍物而到达目标点。

2.2 改进的人工势场法

局部极小值问题是人工势场法的固有问题。在机器人的工作空间内，机器人在势场中受到来自引力势和斥力势的叠加作用，可能导致引力势和斥力势合成后的总势为0。此时，机器人陷入局部极小点，被困在一个局部最小值点周围的势阱中，势场不再对机器人施加作用力，即机器人停留在错误的位置，无法继续向目标点移动。这是因为人工势场法是基于局部搜索的，只考虑当前机器人周围的势场情况而忽略了全局信息。这种局部最小值问题可能导致机器人无法找到最短路径，甚至无法到达目标点。一种典型的局部极小值点情况如图5 所示，描述如下。

图5 局部极小值问题

机器人、障碍物和目标点处于同一条直线，且障碍物位于机器人和目标点之间。此时，引力势和斥力势沿同一条直线而方向相反。这样机器人在移动的过程中，可能在某点处引力和斥力大小相同而抵消，此时机器人所受合力为零，从而陷入局部极小点，无法完成避障任务。

本文针对人工势场法中的局部极小值问题，提出一种改进的人工势场法。改进势场法通过为斥力势函数Urep1增加附加斥力势Urep2对其进行修正。如图6所示，从机器人的位置处向障碍物所在圆作切线，附加斥力势即沿着该切线的方向。

图6 改进势场法的斥力势

在图6 中，Urep1表示传统人工势场法中的斥力势函数，可表示为

根据几何数学的相关知识，平面中有一圆心为(xO,yO)，半径为R 的圆，从圆外一点（x，y）向该圆做切线，其中一条切线的斜率为

那么切点的横纵坐标分别为

则附加斥力势可表示为

最终得到了改进后的斥力势函数：

2.3 基于改进人工势场法的无人船避障策略

得到改进势场法后，需要将其与无人船的运动模型进行结合，从而能够利用该运动模型对算法有效性进行验证。根据改进势场法的基本原理与相关的方程可知，势场中的总势场U 具有使机器人向着靠近目标点而远离障碍物的方向移动的性质。考虑无人船可以通过尾舵来控制其航向，因此将无人船在避障过程中的预设航向指向其所在位置处的总势场U 的方向，从而通过控制航向来完成避障任务，即

综合上文所述，得到了基于改进势场法的无人船避障策略，如图7 所示，具体步骤如下。

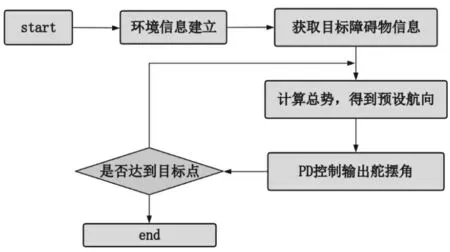
图7 基于改进势场法的无人船避障算法流程图

1）环境信息初始化，捕捉无人船周围一定范围内的环境信息，对障碍物位置进行识别，得到障碍物集合{O1，O2，...，On}，从而建立无人船所处海域的环境模型；

2）计算无人船与障碍物0i(i=1,2,...,n)之间的相对距离di，将di与障碍物影响距离L0进行比较，若di＜L0，则将对应的Osi标记为目标障碍物，得到目标障碍物集合{O1，O2，...，Ok}（k≤n）；

3）根据式（9）计算无人船当前引力势Uy，根据式（15）计算当前斥力势Uc1，Uc2，...，Uck，然后根据式（17）计算总势场U，再由式（16）得到预设航向；

4）将预设航向信号传递给无人船，使用PD 控制器计算舵摆角，使无人船跟随预设航向航行；

5）观测无人船当前运动状态，如达到目标点，则完成避障任务；否则回到步骤3。

2.4 无人船避障性能验证

为了验证上文提出的基于改进势场法的无人船避障算法的可行性，本节利用无人船的运动模型模拟其在障碍物环境中的运动。表1 展示了模拟工况#1—#6 的环境信息。

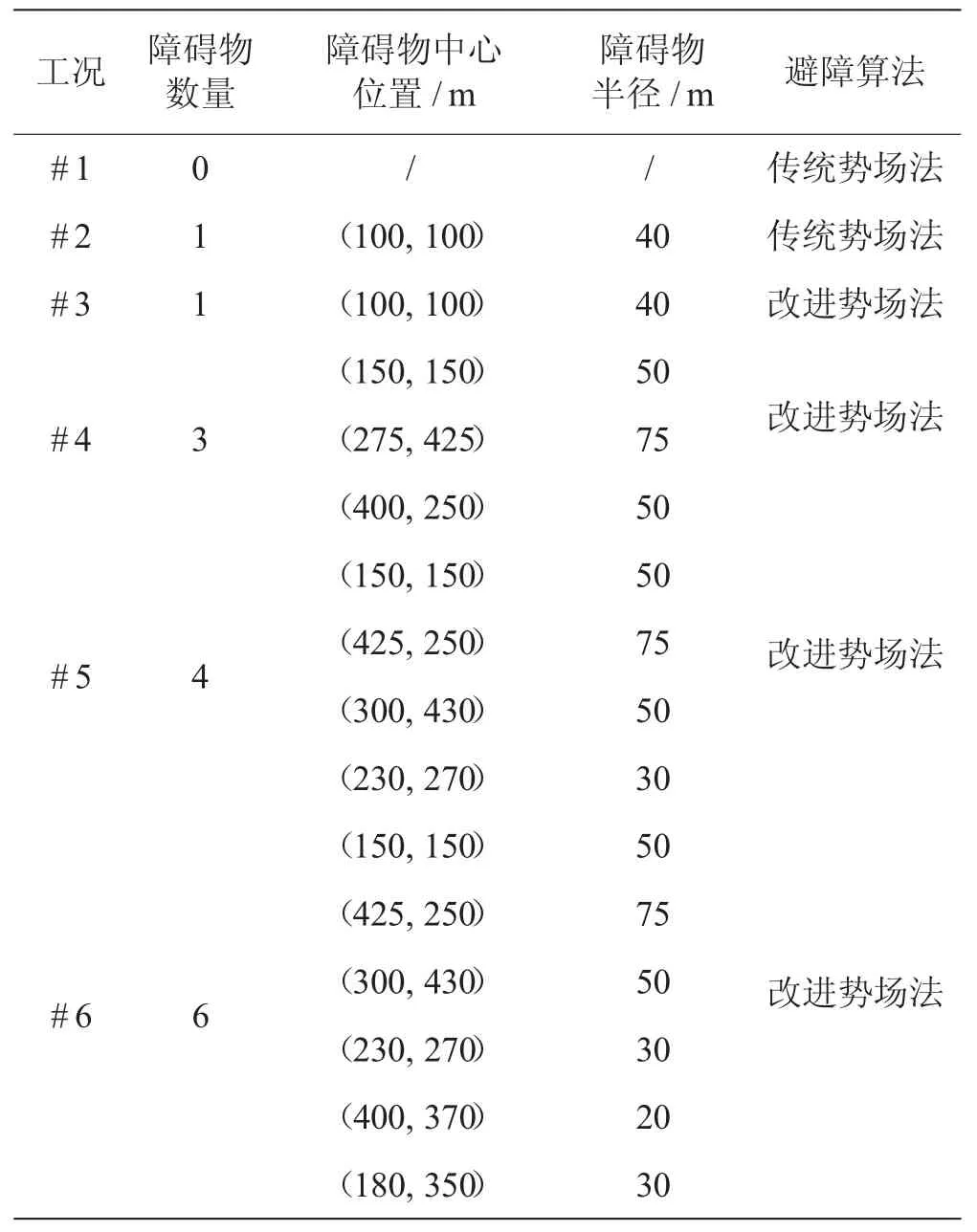
表1 模拟工况

图8 展示工况#1 下的仿真结果。在工况#1 中，环境中仅存在目标点，而没有任何障碍物。此时，无人船在引力势的作用下，沿直线向目标点靠近。

图8 工况#1 仿真结果

图9 展示工况#2 下的仿真结果。在工况#2 中，障碍物位于目标点与无人船初始位置之间的连线上。从图9 中可以发现，当使用传统势场法时，无人船会在局部最小值点附近持续震荡，无法绕开障碍物，导致避障任务失败。

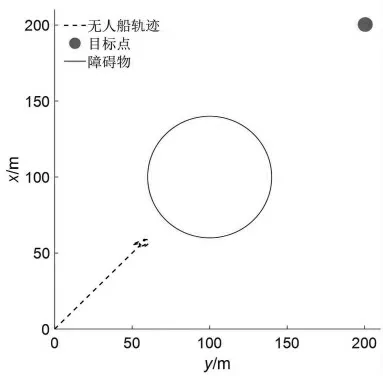
图9 工况#2 仿真结果

图10 展示工况#3 下的仿真结果。从图10 中可以看出，通过使用改进势场法，局部极小值问题得到了解决，无人船成功地避开了障碍物，证明所提出的改进势场法的可行性。

图10 工况#3 仿真结果

图11—图13 展示工况#4—#6 下的仿真结果。在工况#4—#6 中，环境中分别在不同的位置分布3、4、6 个障碍物，由图中可见，无人船在航行过程中与每个障碍物都保持了一定的安全距离，并最终抵达了目标点，顺利地完成了避障任务。仿真结果表明，本文所提出的避障算法能够适应有多个不同障碍物的环境，具有较好的鲁棒性。

图11 工况#4 仿真结果

图13 工况#6 仿真结果

图14 展示了工况#4 下无人船的预设航向随时间变化的情况。根据上文算法设计内容可知，预设航向实际上等价于无人船在虚拟势场受到的总势场方向，也就是为了使无人船避开障碍物需要跟踪的控制信号。通过观察图14 可以看出，在仿真开始阶段，无人船还没有进入障碍物影响区域，只受引力势作用，因此预设航向变化平缓。随着仿真进行，当无人船进入障碍物的影响区域后，由于总势场中叠加了斥力势的变化，因此预设航向也随之发生剧烈的变化，此时无人船进入避障阶段。在无人船驶出障碍物的影响区域后，避障任务完成，此时无人船又仅受引力势的作用，预设航向的变化也重趋平稳。

图14 工况#4 中无人船的预设航向

从图14 可见，本文的避障算法设计合理，在无人船不同的运动阶段能够发出相应的控制信号，从而引导无人船完成避障任务。

3 结论

本文对无人船的智能避障算法进行了研究。首先基于牛顿-欧拉法建立了无人船的运动模型，并设计了PD 航向控制器，通过仿真实验验证了该控制器能够实现对无人船的合理控制。然后，基于人工势场法对无人船的避障问题进行研究，针对传统人工势场法存在的局部极小值问题，通过引入附加斥力势，得到了一种改进的人工势场法，并进行仿真验证。仿真结果表明，本文提出的改进人工势场法能够克服局部极小值问题，并且能够引导无人船在不同的障碍物环境中完成避障任务，证明该算法具备较好的可行性和鲁棒性。