啤酒灌装贮液缸液位控制方法研究
张诗淋
(沈阳职业技术学院,沈阳 110045)
0 引言
啤酒灌装设备集成化程度非常高,诸多工艺可在同一台设备中快速完成。作为啤酒灌装机的关键部件,贮液缸内液位是一个十分重要的参数,其控制精度直接决定啤酒灌装机的整体效率[1,2]。贮液缸内液位的高精度控制可有效避免啤酒量过多、过少、满溢、不足等情况发生。一旦出现上述问题,不仅会造成原料浪费甚至可能导致设备损坏,而且还会提高企业生产成本、维修成本等,因此设计一种贮液缸液位控制方法是很有必要的。一般情况下,啤酒贮液缸内部既有液态啤酒又有一定量气体,二者压力基本一致。贮液缸内液位轻微变化就会对整个灌装过程造成比较大的影响,考虑到诸多干扰因素,啤酒贮液缸内液位控制存在非线性、对干扰等特点[3~5]。当前,啤酒贮液缸内液位控制大多采用传统PID控制,但是仅仅采用PID控制很难解决大延时、大惯性等问题。普通反馈控制和简单的PID控制滞后问题严重,大大降低了整个控制系统品质。为解决此类问题,很多学者进行了众多研究,例如:采用Smith补偿算法,该算法需要事先明确被控对象参数模型,给实际应用带来了诸多不便;采用神经网络等智能控制算法,但是这些算法需要大量训练样本或者过分依赖专家经验,实用性并不高[6~9]。
综合考虑,为解决啤酒贮液缸内液位控制问题,文中以PID控制为基础,采用人工搜索优化算法在线调整PID控制器参数进而提高系统控制精度;基于PLC搭建控制系统,通过实验验证所述方法的可行性和有效性。
1 数学模型
啤酒灌装工艺已经比较成熟,具体流程如图1所示。
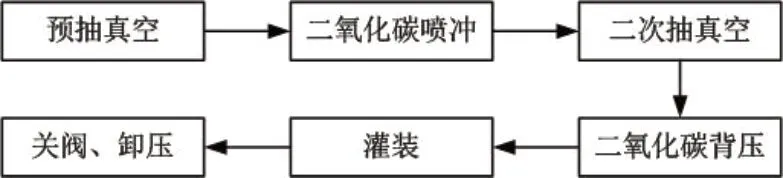
图1 啤酒灌装工艺流程
从图1可以看出:啤酒灌装过程可分为7个步骤,即:预抽真空、二氧化碳喷冲、二次抽真空、二氧化碳背压、灌装、关阀与卸压等。具体流程可描述为:啤酒瓶经洗瓶机清洁、消毒后,会被送到灌装机中;在托瓶气缸的作用下,啤酒瓶被抬升并紧紧地贴在灌装机下料口,这样就会形成一个密闭环境;此时,对啤酒瓶进行抽真空处理,然后将贮液缸内背压二氧化碳冲入瓶中;啤酒瓶内压力会持续升高,当其与贮液缸内气体压力相同时,下料阀打开,进行啤酒灌装;随着啤酒瓶内液体增多,二氧化碳气体会被压入贮液缸内,当啤酒瓶内液位达到一定高度时,就可以停止下料。最后,关闭下料阀和气阀并排除啤酒瓶内部多余气体,至此啤酒灌装完成。
如上所述,啤酒灌装机贮液缸内液位的流动性比较复杂,很难确定其准确的数学模型。为便于分析,可用简化结构表示,如图2所示。其中Q1为啤酒流入量;Q2为啤酒流出量;V1表示进液阀门;V2表示出液阀门;H表示贮液缸内啤酒液位。随着贮液缸内啤酒液位升高,缸内压力会变大,导致啤酒液流出速度变大,即:Q2增加。

图2 啤酒灌装过程简化模型
根据质量守恒定律以及物料平衡定律定律可以得到:

式(1)中,A表示贮液缸底面积。式(1)增量表达式可描述为:

在实际生产过程中,贮液缸液位H和流量之间为非线性关系。为便于处理,需对其进行线性化处理,即认为ΔQ2和ΔH之间成正比,ΔQ2和电液阀V2阻力之间成反比,可描述为:

综合式(1)~式(3)可得:
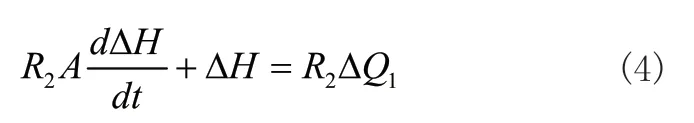
若对上式进行拉普拉斯变换,则有:
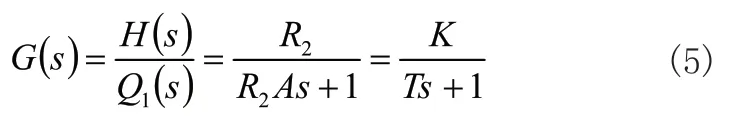
式(5)中,K=R2,T=R2A。
正常情况下,啤酒液流动和贮液缸内液位变化之间存在一定滞后性,可定义延迟时间为τ,因此贮液缸内液位控制系统可近似为一节惯性迟滞系统,那么传递函数可调整为:

2 液位控制器设计
2.1 PID控制
目前,啤酒灌装机贮液缸液位控制大多选用PID控制,在实际应用中,可根据被控对象的单位阶跃响应输出数据利用经验法来确定PID控制器的比例、积分、微分等3个系数。一旦确定,PID控制器并不会根据实际情况自适应调整自身参数,其结构如图3所示。
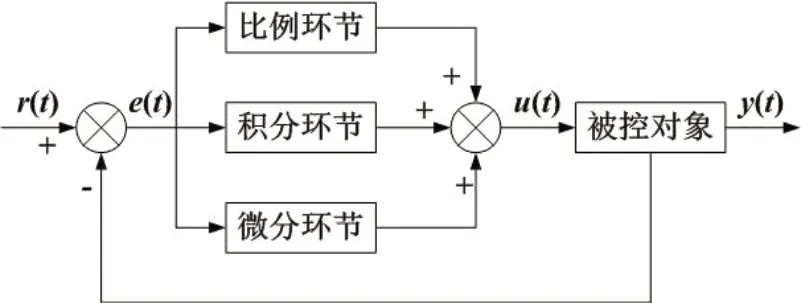
图3 PID控制器结构
PID控制规律的数学表达式可描述为:
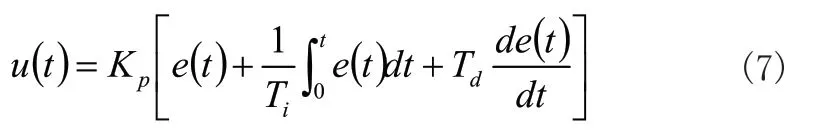
式(7)中,Kp表示比例系数;Ti表示积分时间;Td表示微分时间。考虑到实际控制过程中,采样得到的数据都是离散的,因此需要将式(7)离散化,即:
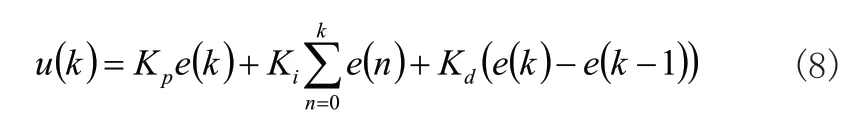
式(8)中k表示采样序号;e(k)表示第k次采样液位偏差;e(k-1)表示第k-1次采样液位偏差;u(k)表示第k次控制输出;Ki表示积分系数;Kd表示微分系数。
由式(8)可以看出,通过调节Kp、Ki、Kd可以改变控制输出u(k),最终使控制系统满足相关工艺要求。综上所述,控制系统能否满足相关要求,关键在于参数Kp、Ki、Kd的选择。
2.2 基于SOA的PID参数优化
人群搜索优化算法(SOA)作为一种新型群体智能算法,最近在控制领域的应用比较广泛,因此文中选择该算法来实现PID控制器参数优化。以传统直接搜索算法为基础,将搜索队伍作为种群,以各搜索者位置作为候选解。通过模仿人类搜索过程中对方向、位置的推理判断来实现问题最优解求解,整体来说,SOA算法具有收敛速度快、稳定性高等特点[10~14]。
人群搜索优化算法可描述为:
假设搜索空间维度为D,该空间共有S个搜寻个体,那么个体i实际位置可表示为:
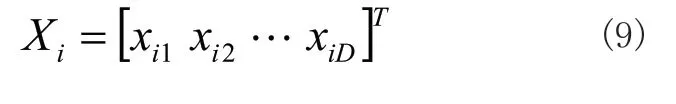
考虑到PID控制器存在3个控制参数,所以人群搜索优化算法的空间维度设定为3。
适应度函数可使算法根据控制目标要求不断进化。为使控制系统具有比较良好的动态特性,可采用液位误差绝对值的时间积分最小作为目标函数。为避免控制量过大,可在目标函数中加入平方项,即:

式(10)中ζ1、ζ2、ζ3都是权值系数而且满足ζ3>>ζ1。另外,为减小系统超调量,可采用惩罚控制,通过仿真和具体实验,权值系数ζ1、ζ2、ζ3可分别选取0.999、0.001、100。
人群搜索优化算法可利用模糊系统的逼近能力来模拟人类智能搜索行为,进而确定目标函数和搜索步长之间的关系,那么搜索步长可表示为:

式(11)中αij表示j维搜索空间的搜索步长;δij表示高斯隶属度函数参数;uij表示j维搜索空间目标函数值i的隶属度。
人类搜索行为主要包括利他行为、利己行为、预动行为等,通过对人类搜索行为的分析、推理可以确定具体搜索方向,即:
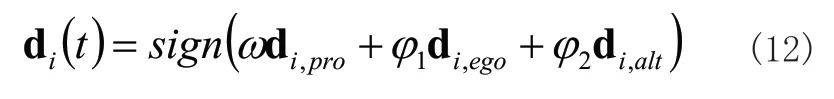
式(12)中di,pro表示第i个搜索个体的预动方向;di,ego表示第i个搜索个体的利己方向;di,alt表示第i个搜索个体的利他方向;ω表示惯性权值,随着迭代次数不断增加,ω数值可从0.9线性递减至0.1;φ1、φ2为常数,大小介于0~1之间。
基于人群搜索算法的PID控制器参数优化过程可描述为:
第一步:搜索者位置初始化,同时系统随机生成初始位置矩阵;
第二步:计算搜索者的适应度。
第三步:比较搜索者当前位置和历史最佳位置,选择并保存搜索者最佳位置同时更新搜索者位置;
第四步:比较搜索者最优位置和人群历史最优位置,如果当前搜索者位置更好则替换、更新种群历史最优位置;
第五步:判断是否达到迭代次数或满足结束条件,如果不满足,则返回第二步;如果满足,则结束循环。基于SOA-PID算法的啤酒灌装贮液缸液位控制系统如图4所示。
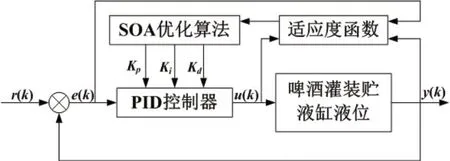
图4 啤酒灌装贮液缸液位控制系统
3 实验研究
3.1 系统搭建
为验证所述控制方法的可行性和有效性,文中进行了相关实验研究。实验系统以PC机作为上位机,集成SOA优化算法和PID控制方法;同时上位机可实时监控灌装机实际工作情况。PLC为核心控制器,PLC可采集啤酒灌装机贮液缸内液位,然后将其传送给PC机,PC机利用集成算法得到相关控制量并发送给PLC;PLC根据控制量调节进水阀门和出水阀门开度,进而实现贮液缸内液位自动控制[15,16]。
控制系统主控制器型号为S7-200PLC,其硬件接线如图5所示,I/O口分配情况如表1所示。
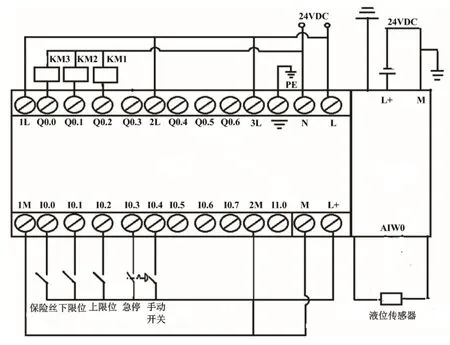
图5 PLC硬件接线图

表1 I/O地址分配t
3.2 实验结果
实验条件设定如下:罐装液体为青岛纯生啤酒原液;灌装体积为500mL试验条件如下:灌装液体为矿泉水;灌装标准体积为500mL;灌装车间环境温度为18℃~24℃;灌装速度设定为80瓶/min。作为对比,可选用文中所述方法和传统PID控制方法分别进行实验。
实验过程中,设备正常运行10min后开始检测,将灌装标准体积和实际检测结果进行比较,进而确定灌装精度。从实验结果中随机挑选20组数据,实验结果如表2所示。

表2 实验结果
从实验结果可以看出:采用传统PID控制,灌装体积偏差绝对值的最大值为5mL,平均值为2.44mL,灌装体积偏差较大、波动幅度也比较大;采用文中所述方法,灌装体积偏差绝对值的最大值为1mL,平均值为0.36mL,灌装体积偏差较小、波动幅度也比较小;与传统PID控制相比,采用文中所述方法可以灌装精度提高约5倍。实验结果表明:采用SOA算法优化PID控制器参数可以提高啤酒灌装精度,整个系统的稳定性和鲁棒性明显提高,能够满足啤酒灌装工艺对精度的要求。
另外,在响应速度方面,采用文中所述方法并没有明显提高系统响应时间,算法执行效率与PID控制方法基本相当。
4 结语
针对啤酒灌装机贮液缸液位控制非线性、滞后性等问题,文中设计了一种SOA-PID液位控制方法。利用人工搜索优化在线调整、优化PID控制器参数,进而提高啤酒灌装精度。实验结果表明:在确保算法执行效率的前提下,所述啤酒灌装贮液缸液位控制方法可以明显提高啤酒灌装精度,能够满足相关工艺要求。考虑到影响啤酒灌装精度的因素比较多,下一步可从干扰因素分析入手进一步提高啤酒灌装精度。

