不平衡负载下四桥臂逆变器的积分滑模控制
乔 和,杨涵杰
(辽宁工程技术大学 电气与控制工程学院,葫芦岛 125105)
0 引言
近年来,分布式发电技术以充分利用各种可再生能源、高可靠性、低污染的优点迅速发展,多种分布式电源以微网的形式接入大电网,凭借可靠灵活的运行特点引起广泛关注[1~4]。离网模式下的微网要求对分布式电源进行协调控制,保证电网失去外部供电或出现故障时对重要负荷的持续供电。离网运行时微网所需的负载功率主要由逆变器电源所供给,交流负荷里含有大量单相与三相负载易导致输出电压不平衡,对微电网系统的稳定性造成严重影响,所以进行不平衡负载下逆变器控制的研究极其重要[5~7]。
三相四桥臂逆变器具有结构简单、体积小和直流电源转化率高等优点,为了保证其在不平衡负载下的有效运行,采取了许多控制方法。传统的比例积分控制器(Proportion Integral,PI)简单易实现,通常用于在dq坐标系下跟踪恒定参考信号,但系统整体性能会受到参数摄动和负荷变化的影响,尽管采用正负序分离的方法能够改善性能,但是增大了计算负担[8];比例谐振(Proportion Resonant,PR)控制器可用于abc和αβ坐标系并实现零稳态误差,但对频率变化敏感,会降低系统的整体性能[9];模型预测控制(MPC)和无差拍控制(DBC)方法具有快速的动态响应特性,但均需要精确的数学模型,对模型参数失配的敏感性较高,且模型预测控制需要为所有可用电压矢量计算成本函数,给四桥臂逆变器带来很大的计算负担[10]。
滑模控制(Sliding Model Control,SMC)的不连续性与逆变器的变结构特点相符,适合采用闭环控制的逆变器。文献[11~13]研究了单相和三相逆变器的滑模控制器,保证在线性和非线性负载情况下,输出电压的总谐波失真均较小,但存在输出电压抖振较大的问题;文献[14,15]针对三相逆变器,提出了基于状态空间方程的积分滑模控制器,抑制了输出电压的高频抖振且对外部干扰具有较强的鲁棒性,但模型推导较为复杂。本文提出一种四桥臂逆变器的积分型滑模控制器,保证逆变器在不平衡负载下输出电压的高度对称性。首先利用矢量控制建立dq0旋转坐标系下的数学模型,然后构建系统状态的积分滑模面,给出了控制律的详细推导过程;并采用李雅普诺夫函数稳定性理论验证了系统的稳定性;最后通过仿真与PI控制器进行对比,验证了所提控制器的正确性和有效性。
1 三相四桥臂逆变器模型
三相四桥臂逆变器的拓扑结构如图1所示,其中Vdc为直流电源电压,va、vb、vc、vn为四桥臂所对应的电压,ila、ilb、ilc为三相电感电流,iln为中性线补偿电流,L为滤波电感,C为滤波电容,vAG、vBG、vCG为三相负载电压,ia、ib、ic为三相负载电流,Za、Zb、Zc为三相负载阻抗。
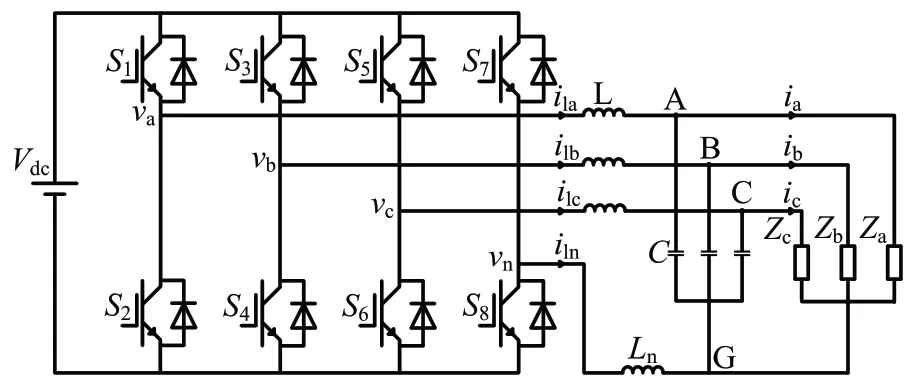
图1 三相四桥臂逆变器拓扑
设da、db、dc、dn为四桥臂导通比,n为母线中点电位,可得三相四桥臂输出电压van、vbn、vcn为:
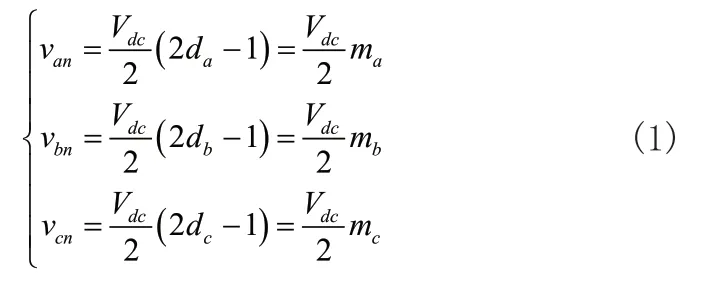
其中,mx=2da-1,x=a、b、c。
根据基尔霍夫电压和电流定律,四桥臂逆变器系统中各量之间存在如下关系:

其中r和rn分别为滤波电感L和中线电感Ln的寄生电阻。
dq0旋转坐标系由abc静止坐标系逆时针旋转ω后得到,由矢量合成原则可得变换关系为:
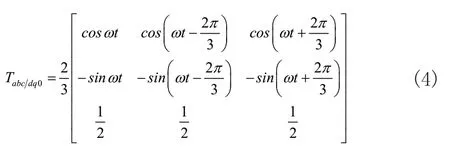
式(2)和式(3)对应旋转坐标系dq0的模型为:
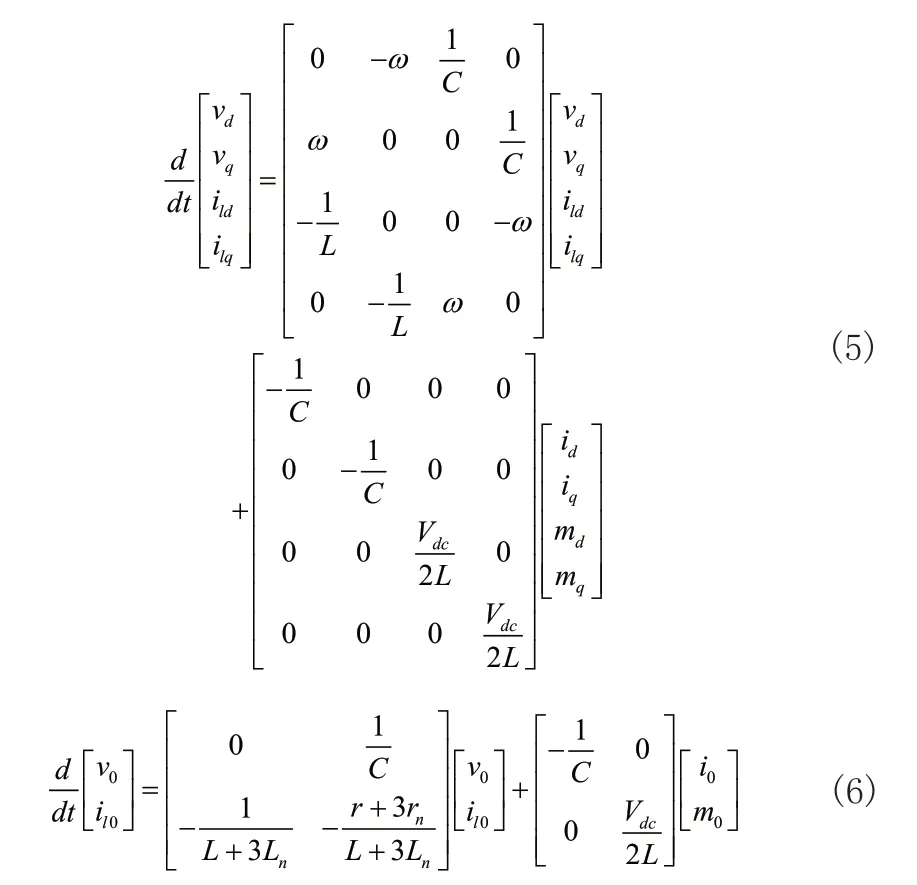
由式(5)和式(6)可得四桥臂逆变器的系统模型为:

2 积分型滑模控制器
2.1 控制器设计
积分型滑模控制器的设计是定义一个良好的滑模面和控制律,为了方便计算,首先简化四桥臂逆变器的系统模型可得:
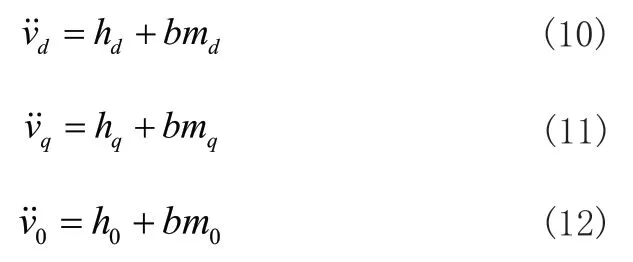
其中:

为了实现滑模控制,通常利用跟踪误差作为状态变量,由此定义滑模控制的输入量为:
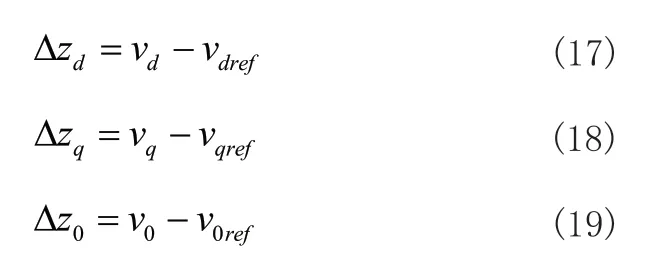
其中vdref、vqref、v0ref分别为d、q、0轴的参考电压。
为了消除控制器中被跟踪信号的导数项,在传统滑模面设计的基础上,引入跟踪误差的积分项,构成dq0轴的积分滑模面为:
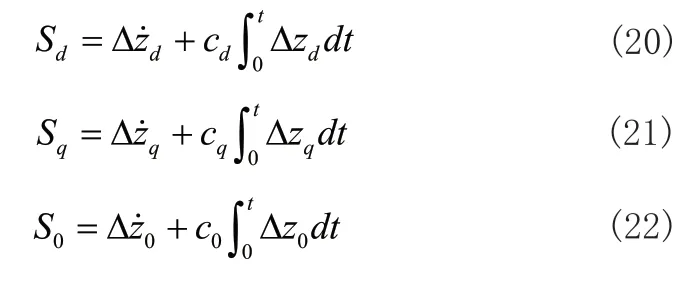
其中cd、cq、c0为设计的滑模面参数。
为了便于后文计算,对dq0轴输入量求二阶导并分别代入到式(20)~式(22)的一阶导数中可得:

由于参考电压往往设定为常数,dq0轴参考电压的二阶导数为零,并将简化的四桥臂逆变器系统模型代入式(23)~式(25)中可得:

其中k表示趋近于滑模面的速度,kd>0、kq>0、k0>0为积分滑模控制器常数,sgn(·)为符号函数,表示为:
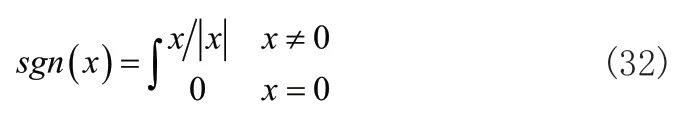
2.2 稳定性分析
为了保证四桥臂逆变器系统的稳定性,定义李雅普诺夫函数:
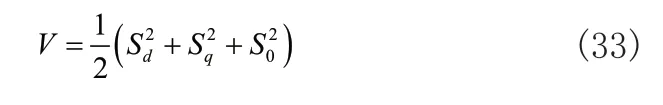
从定义的Lyaponov函数可以看出,函数V在除了原点之外的所有值均大于零,将设计的控制律代入到式(33)的一阶导数中可得:

结合结论V≥0可知,该系统满足李雅普诺夫稳定性定理,可以认为此系统是渐近稳定的。
3 仿真结果分析
为了验证积分滑模控制器的性能,在MATLAB/Simulink中进行负荷和系统参数变化的仿真。系统参数:直流电源电压Udc=720V,LC滤波器中L=2mH,C=300μF,寄生电阻R=Rn=0.001Ω,中线电感Ln=440μH,开关频率fs=20kHz,ω=100rad/s。积分滑模控制器参数:Cd=5,Cq=5,C0=1,Kd=5,Kq=10,K0=2。
当四桥臂逆变器接不平衡阻性负载时,令Za=15Ω,Zb=18Ω,Zc=12Ω,图2和图3为两种控制下逆变器输出电压电压和电流波形图。经对比可以看出,积分滑模控制下三相电压付幅值差异较小,在t=0.3s时同时并入5Ω纯阻性负载,电流增大且持续时间为0.1s,输出电压在受到干扰前后没有发生明显变化,仍保持一定的对称性。
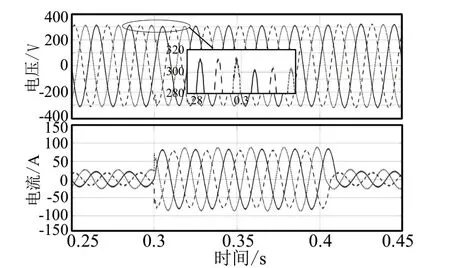
图2 PI控制下输出电压和电流波形图(不平衡阻性)
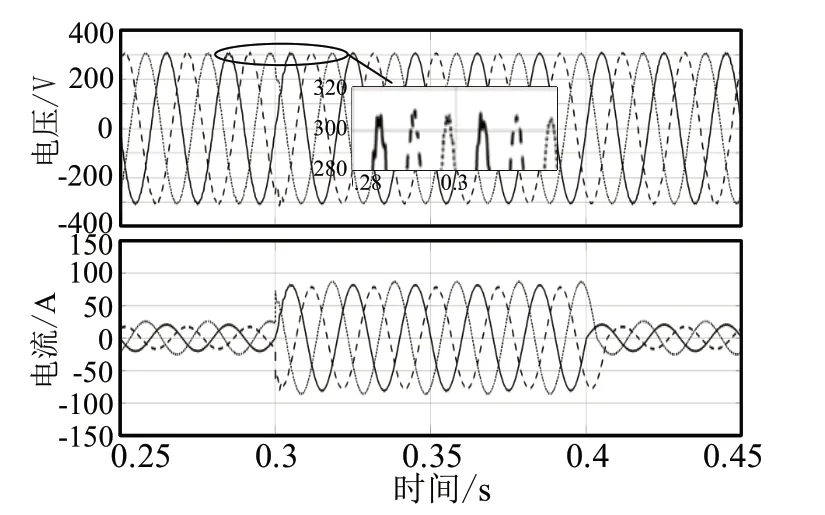
图3 ISMC控制下输出电压和电流波形图(不平衡容性)
图3和图4为四桥臂逆变器接不平衡容性负载时,采用PI控制和积分滑模控制下逆变器的输出电压和电流波形图。
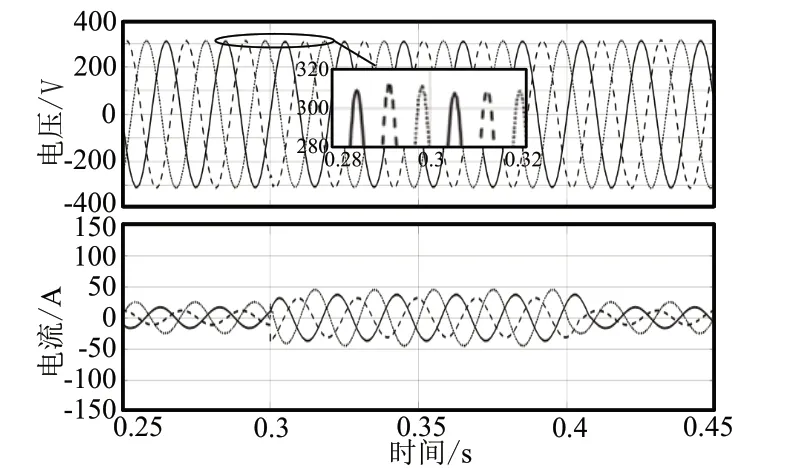
图4 PI控制下输出电压和电流波形图(不平衡感性)
三相负载分别为:15Ω,290μF;25Ω,300μF;5Ω,280μF,由仿真结果可以看出,积分滑模控制下输出电压对称性较高,在t=0.3时突并10Ω,280μF容性负载,输出电压无明显波动,仍保持较高的对称性。
当四桥臂逆变器接不平衡感性负载时,图5和图6分别为采用PI控制和积分滑模控制下逆变器的输出电压和电流波形图,三相负载分别为:15Ω,10μF;25Ω,15μF;8Ω,5μF,从图中可以看出,0.3s时突并5Ω,10μF感性负载,当电流发生变化时,积分滑模控制下输出电压不随电流的改变而发生改变。

图5 ISMC控制下输出电压和电流波形图

图6 PI控制下输出电压和电流波形图

图7 ISMC控制下输出电压和电流波形图
通过上述三种负载变化的仿真实验可以看出,积分滑模控制器的控制效果优于传统PI控制,稳态时三相电压对称性较高,负载突变时具有更好的抗干扰能力和较强鲁棒性。
图8为电感变化时逆变器输出电压和电流波形图,在t=0.2s时电感变化为给定值的200%,通过仿真结果可以看出,滤波电感的变化对输出电压对称性几乎无影响。
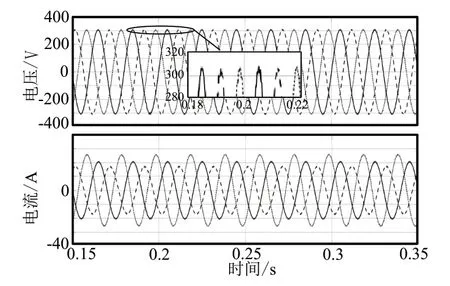
图8 ISMC控制下电感变化输出电压和电流波形图
4 结语
本文针对四桥臂逆变器在不平衡负载下输出电压不平衡的问题,提出了一种基于矢量控制的积分型滑模控制器。推导了四桥臂逆变器系统在dq0旋转坐标系下的数学模型,并基于此模型结合滑模控制原理给出了控制器设计的详细过程,通过李雅普诺夫函数稳定性理论验证了系统的稳定性。仿真分析结果表明:所提出的积分型滑模控制器计算量小,能够消除系统参数摄动带来的影响;系统输出电压稳态精度高同时对于时变的负荷干扰具有良好的动态性能。

