粤港澳大湾区高科技人才吸引力空间差异与收敛性研究——以珠三角九市为例

邓利方，陈 熙

(1. 中共广东省委党校 中国特色社会主义研究所，广东 广州 510053；2.中共广东省委党校 理论经济学部，广东 广州 510053)

科技创新对推进产业升级、提升区域经济高质量发展的影响日益突出，高科技人才资源作为科技创新载体，已成为各国综合国力竞争的核心要素。而科技迅猛发展使得各国均面临高科技人才供需失衡困境，国际社会迫切要求提升本地对人才特别是高科技人才的吸引力[1]，以在人才争夺战中掌握主动权。习近平总书记在中国共产党第二十次全国代表大会上深刻阐明新阶段人才工作的重点任务：“加快建设世界重要人才中心和创新高地，促进人才区域合理布局和协调发展，着力形成人才国际竞争的比较优势。”[2]面对逐步减退的“人口红利”形势，作为未来的高水平人才高地之一的粤港澳大湾区，亟须加速朝“人才红利”转变，通过实施兼收并蓄、包容开放的高科技人才引进政策，营造令人心驰神往的高科技人才环境，以形成战略支点与雁阵格局。因此，定量研究粤港澳大湾区城市高科技人才吸引力，分析人才吸引力区域协调发展现状，并提出具有竞争力的引才用才政策建议，对湾区城市提高自身高科技人才吸引力，打造利于全球高端科技人才集聚的人才环境，实现2035年人才强国战略大有裨益。

一、文献综述

经济合作与发展组织(Organization for Economic Co-operation and Development，OECD)起草的《堪培拉手册》中将成功完成高等教育，与不具备学历但在科技领域取得科技职业资格的两类人员视为高科技人才。本文基于OECD定义进行探讨，认为高科技人才吸引力是人力资本受某种驱动在空间上的流动结果，进一步说，是高科技人才充当生产要素在区域内的集聚外部表征[3]。

人才集聚的形成是人才自身微观因素与经济社会宏观因素共同作用结果。人才自身的微观因素包括人才的主观流动意愿、人才成长预期、人才消费能力；经济社会宏观因素则囊括经济发展水平、产业集聚、文化教育、政策制度。此外，对人才集聚因素的综合分析也不断涌现，其认为人才集聚的形成不囿于单一因素，而是多种因素共同形成的反映。经济发展、科技创新、文化教育、社会保障、生活环境、制度环境及公共服务因素的组合常被纳入科技人才集聚的影响体系研究范畴[4]。但对人才集聚的关键因素尚未达成普遍共识，霍丽霞等[5]通过多元线性回归分析，将科技创新视为关键性因素。李作学等[6]则运用模糊集定性比较分析法发现文化教育是科技人才集聚的关键因素。

人才集聚的影响因素研究为高科技人才吸引力的定量分析提供理论基础，目前对人才吸引力的定量分析主要围绕指标体系构建法展开。早期研究中，学者多采用单一方法构建人才吸引力评价体系，大致可分为以层次分析法[7]为代表的主观赋权法和以主成分分析法[8]为代表的客观赋权法两类。但鉴于两类方法均存在局限性与不严谨性，人才吸引力评价体系的构建由单一法向复合法转变。穆晓霞等[9]从经济发展、文化教育、生活环境等方面筛选确立人才集聚指标，建立熵权法与灰色聚类法的复合评价模型，以对中西部六省人才集聚效应进行评价。叶晓倩等[10]基于舒适物理论复合熵值法与聚类分析法，对33个人口规模较大、人均可支配收入较高的代表性城市人才吸引力进行评分与分类。崔少泽等[11]综合考虑经济发展、科技创新及生活环境等影响因素，综合等权赋值法、梯度赋值法、主成分分析法对指标体系的不同层级指标赋权，对深圳及同层次城市人才吸引力进行评价。

无论是从研究方法、研究层面，还是从研究对象来看，学界对人才吸引力的研究不断深化。纵观现有的研究成果，存在几点不足：第一，大多数学者倾向于利用地区的截面数据对区域人才吸引力现状进行解读，对于相关指标的时间序列数据和面板数据缺乏分析；第二，研究大多从整体层面对区域人才吸引力进行探讨，考虑群体间异质性，以高科技人才为研究对象的成果相对较少；第三，现有研究通过建立综合评价指标体系测算人才吸引力后，仅通过简单对比加以分析，对吸引力的空间差异及空间收敛性鲜有定量研究。

基于此，本文尝试从以下三个方面对现有研究作出边际贡献：第一，选取2010—2020年珠三角九市的各项指标面板数据，综合群决策法与极差标准化熵值法对高科技人才吸引力指标权重及吸引力得分进行测算，避免了唯主观论与唯数据论所致的偏差；第二，将研究对象细化为高科技人才，充分考虑高科技人才的异质性需求，构建适用于评价高科技人才吸引力的评价指标体系；第三，基于Dagum基尼系数、Kernel核密度估计、σ收敛分析与β收敛模型对高科技人才吸引力区域空间差异及空间收敛性予以定量描述。

二、体系构建、研究方法与数据来源

(一)高科技人才吸引力评价指标体系的构建

个体心理学指出，涉及行为的发端、方向、强度和持续性，推动人从事某种事情的念头常被称为动机。高科技人才吸引力大小建立在人才受动机驱使强弱基础上，而动机是在需求的基础上产生的。当人才的某种需求没有得到满足时，它会推动人才去寻找满足需求的对象，从而产生活动动机。当人才发现某区域更能满足其生理或心理上的需求时，其将会迁移至该区域，多数人才的普遍性选择使得该区域的人才吸引力水平更高。

目前，需求领域的代表性理论有马斯洛需求层次理论、赫茨伯格需要双因素理论、ERG需要理论等。相较其他理论，ERG需要理论与个体差异的常识相一致，且与国内学者关于人类需求多样性、潜在性和可变性特征的观点更为接近。

ERG需要理论是奥尔德弗在马斯洛需要层次理论的基础上，提出的一种新人本主义需要理论[18]。其认为，人们共存在三种核心的需要，即生存(existence)的需要、关系(relatedness)的需要和成长(growth)的需要。

本文通过结合ERG需要理论基础，从高科技人才需求入手，选取人才流动生存动机、人才价值保障机制、人才成长环境作为高科技人才吸引力指标确立的子目标。

1. 人才流动生存动机

ERG需要理论中的“生存的需要”，即生理和安全需求(如衣、食、行等)，其关系到人的生存与生产活动践行。该需要的满足是区域提高高科技人才吸引力的首要前提，高科技人才生存需要遭到胁迫，生理机能下降，无法支撑其在高新技术领域进行后续的创新活动。在此，本文将高科技人才在区域的生存需要定义为“人才流动生存动机”，借鉴李燕萍等[13]、孙博等[14]对个体生存动机的衡量指标，用经济发展水平、生活环境状况以及自然环境状况来衡量人才流动生存动机。

2.人才价值保障机制

除考虑高科技人才自身需求以提高区域短期人才吸引力外，还需考虑长期下的持续吸引力。从ERG需要理论中的“关系的需要”来看，高科技人才具有对家庭关系与社会关系的需求。家庭关系的需求从高科技人才家庭成员处获取，因此区域对高科技人才的吸引，还应考虑人才相关家庭成员的需求。然而，由于本文基于宏观视角展开研究，囿于对数据的可用性，对其家庭关系不展开深入探究。社会关系的需求则依靠人才价值保障机制的建立，其利于满足高科技人才对社会地位的需要，加强了其在区域内社会关系网络的建立，是区域提高高科技人才吸引力的后续保障。在此，将高科技人才在区域关系的需要定义为“人才价值保障机制”，借鉴侯慧丽[15]、林李月等[16]及崔少泽等[11]的研究成果，采用人才市场环境及社会保障管理来衡量人才价值保障机制。

3.人才成长环境

与一般的人力资源不同，高科技人才谋求发展的内在意愿更强烈。区域可提供的高科技人才成长环境条件越优越，高科技人才便越可能得到长足的发展，其受到的成就激励越高。这也恰恰印证了ERG需要理论中的“成长的需要”，即个人自我发展和自我完善的需求，这种需求通过创造性地发展个人的潜力和才能、完成挑战性的工作而得到满足，是区域提高高科技人才吸引力的核心竞争力。在此，本文将高科技人才在区域的成长发展需要定义为“人才成长环境”，借鉴蒋茁等[17]及乔锦忠等[18]的研究成果，采用教育培训机会、科技创新氛围及信息共享条件来衡量人才成长环境。

结合现有研究成果和社会调查结论，进一步将影响高科技人才流动生存动机的主要因素归纳为经济发展水平、自然环境状况和生活环境状况三个方面；影响高科技人才价值保障机制的主要因素归纳为人才市场环境和社会保障管理两个方面；影响高科技人才成长环境的主要因素归纳为教育培训机会、科技创新氛围和信息共享条件三个方面。

此外，为了使指标体系易于量化，且基于城市统计工作的滞后性以及同一截面上数据的完全性、可操作性及可比性，本文进行了要素分析、资料筛选、专家评价，选取28个易于量化的二级指标，确立高科技人才吸引力评价指标体系架构(见表1)。

表1 珠三角高科技人才吸引力评价指标体系架构

(二)研究方法

为对粤港澳大湾区2010—2020年高科技人才吸引力水平及区域协调性进行分析，首先，本文结合群决策法与熵值法构造高科技人才吸引力评价模型并对各城市历年高科技人才吸引力进行测度；其次，运用Dagum基尼系数测度三类都市圈高科技人才吸引力区域差距演变特征；再次，运用Kernel核密度估计测度高科技人才吸引力时变特征；最后，基于薛鹏飞等[27]于人才学领域运用收敛理论展开的拓展研究，尝试运用σ收敛分析与β收敛模型探究粤港澳大湾区高科技人才吸引力收敛特征。

1. 高科技人才吸引力评价模型

(1)基于群决策法的一级指标权重确定

第一步，构造判断矩阵。

专家根据1至9比较尺度，对准则层与一级指标层的同层属性进行两两比较打分，得到互补判断矩阵，如式(1)所示：

(1)

第二步，一致性检验。

对互补判断矩阵进行一致性检验，保证专家在打分时对同层属性重要性的比较具有逻辑上的一致性。

(2)

式中，λmax为判断矩阵B(m)的最大特征值，m为矩阵B(m)的阶数，CI为一致性指标。

(3)

式中，RI为平均随机一致性指标，CR为一致性比例。

通过式(3)，对得到的每一个矩阵进行一致性比例的计算。若CR<0.1则表示通过一致性检验；反之则需重新构造互补判断矩阵。

第三步，权重计算。

(4)

式中，Wi′表示判断矩阵对应的权重向量，ai′， j ′表示第i′个指标对第j′个指标的相对重要性。

(2)基于熵值法的二级评价指标权重确定

第一步，计算第i个城市在t年的第j个一级指标下第k个二级指标的样本值占该指标的比重。

(5)

式中，xi，t，j，k为第i个城市在t年的第j个一级指标下第k个二级指标的样本值；i=1，2，…，n；t=2010，2011，…，2020；j=1，2，…，9；k=1，2，…，m。

第二步，计算第j个一级指标下第k个二级指标的熵值。

(6)

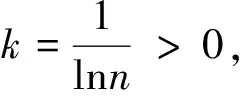
第三步，信息熵冗余度计算。

dj，k=1-ej，k，j=1，2…9；k=1，2，…，m

(7)

式中，dj，k为信息熵冗余度。

第四步，二级指标权重计算。

(8)

式中，qj，k为二级指标权重。

(3)高科技人才吸引力计算

采用群决策法和熵值法分别对一级评价指标与二级评价指标权重确定，构造高科技人才吸引力测度模型。

(9)

式中，Ai，t表示第i个城市在t年高科技人才吸引力的值；Wj表示一级指标的权重；qj，k表示二级指标的权重。

2. Dagum基尼系数

(1)总体基尼系数的计算

运用Dagum基尼系数，对各城市高科技人才吸引力差异进行刻画：

(10)

(2)总体基尼系数的分解

进一步根据Dagum基尼系数的分解方法，可将各区域高科技人才吸引力分解为组内差距贡献Gw、 组间差距贡献Gnb、超变密度贡献Gt，后两者共同衡量组间不平等Ggb=Gnb+Gt， 满足等量关系式：

G=Gw+Ggb=Gw+Gnb+Gt

(11)

(3)组内差距贡献Gw的计算

组内差距贡献Gw的具体表达式为：

(12)

(13)

(14)

(15)

(4)组间差距贡献Gnb的计算

组间差距贡献Gnb的具体表达式为：

(16)

(17)

(18)

(19)

(20)

式中，Gjh为区域j与区域h的组间基尼系数；Djh为区域j与区域h间高科技人吸引力的相互影响；djh为区域间高科技人才吸引力差值，即区域j与区域h中所有Aj，i-Ah，r>0的样本值加总的数学期望；pjh为超变一阶矩阵，即区域j与区域h中所有Aj，i-Ah，r<0的样本值加总的数学期望；Fj(A)为区域j的累计密度分布函数。

(5)超变密度贡献Gt的计算

超变密度贡献Gt的具体表达式为：

(21)

3. Kernel核密度函数

(1)核函数确定

Kernel核密度可分为线性核、高斯核、三角核等多种形式，本文选择最为常用的高斯核函数进行估计，其表达式为：

(22)

(2)核密度估计式确定

当随机变量X1，X2，…，Xn独立同分布，假设Xi(i=1，2，…，n)的密度函数为f(x)，则核密度估计式可记为：

(23)

4.σ收敛

σ收敛通过研究高科技人才吸引力的离差随时间推移发生的变化，旨在从存量角度揭示地区高科技人才吸引力的收敛特征。当离差趋于下降时，表明地区吸引力存在σ收敛，反之则存在σ发散，具体计算公式如下：

(24)

5.β收敛

β收敛通过研究高科技人才吸引力水平的增长速度随时间推移发生的变化，旨在从增量角度揭示地区高科技人才吸引力的收敛特征。当收敛常数β显著为负时，表明吸引力存在β收敛，反之则存在β发散。根据是否考虑外界因素，可将β收敛进一步划分为绝对β收敛与条件β收敛[22]。

(1)绝对β收敛模型

绝对β收敛是指在外界条件完全相同时，各城市的高科技人才吸引力随时间推移逐渐收敛至相同水平，即高科技人才吸引力低水平城市较高水平城市具有更高增速。借鉴Barro等[23]提出的经典研究范式，本文对城市个体进行固定，设定绝对β收敛模型形式为：

(25)

式中，β为收敛常数；μi为个体固定效应；εi，t为随机误差项。

(2)条件β收敛模型

条件β收敛模型则是在绝对β收敛模型基础上，考虑其他变量对高科技人才吸引力水平的增长速度影响。借鉴Barro等[24]对条件β收敛模型的处理，在式(25)基础上，加入其他控制变量，设定条件β收敛模型形式为：

(26)

式中，Xi，t，k为控制变量。

(3)收敛速度s与半生命周期c的计算

收敛速度s为高科技人才吸引力低水平地区追上高水平地区的速度，半生命周期c则为消除一半区域吸引力差距所耗费的时间，具体计算公式如下所示：

(27)

(28)

式中，T为考察周期，参考王维[25]的处理方法，本文设定T=1。

(三)数据来源

为研究粤港澳大湾区高科技人才吸引力水平空间差距及收敛状况，本文选取珠三角九个地级市作为研究对象(由于港澳地区数据存在较多缺失值，故未将香港与澳门两地纳入考虑范畴)，选取2010—2020年为体系构建、空间差异与收敛特征的考察期。指标体系二级指标D1～D28数据来自广东省及各地市历年统计年鉴与《中国城市统计年鉴》；控制变量人口密度、金融机构贷款余额及法院案件一审结案率数据来自历年《广东统计年鉴》《中国城市统计年鉴》及《广东社会统计年鉴》，对缺失数据则采用平均值进行赋值补充。

三、结果分析

(一)珠三角高科技人才吸引力得分

综合运用群决策法与熵值法可对评价指标体系各级指标权重进行确定，权重结果如表1所示。据此建立高科技人才吸引力计量模型，可得2010—2020年珠三角高科技人才吸引力水平综合与细项得分及排名结果，如表2和表3所示。

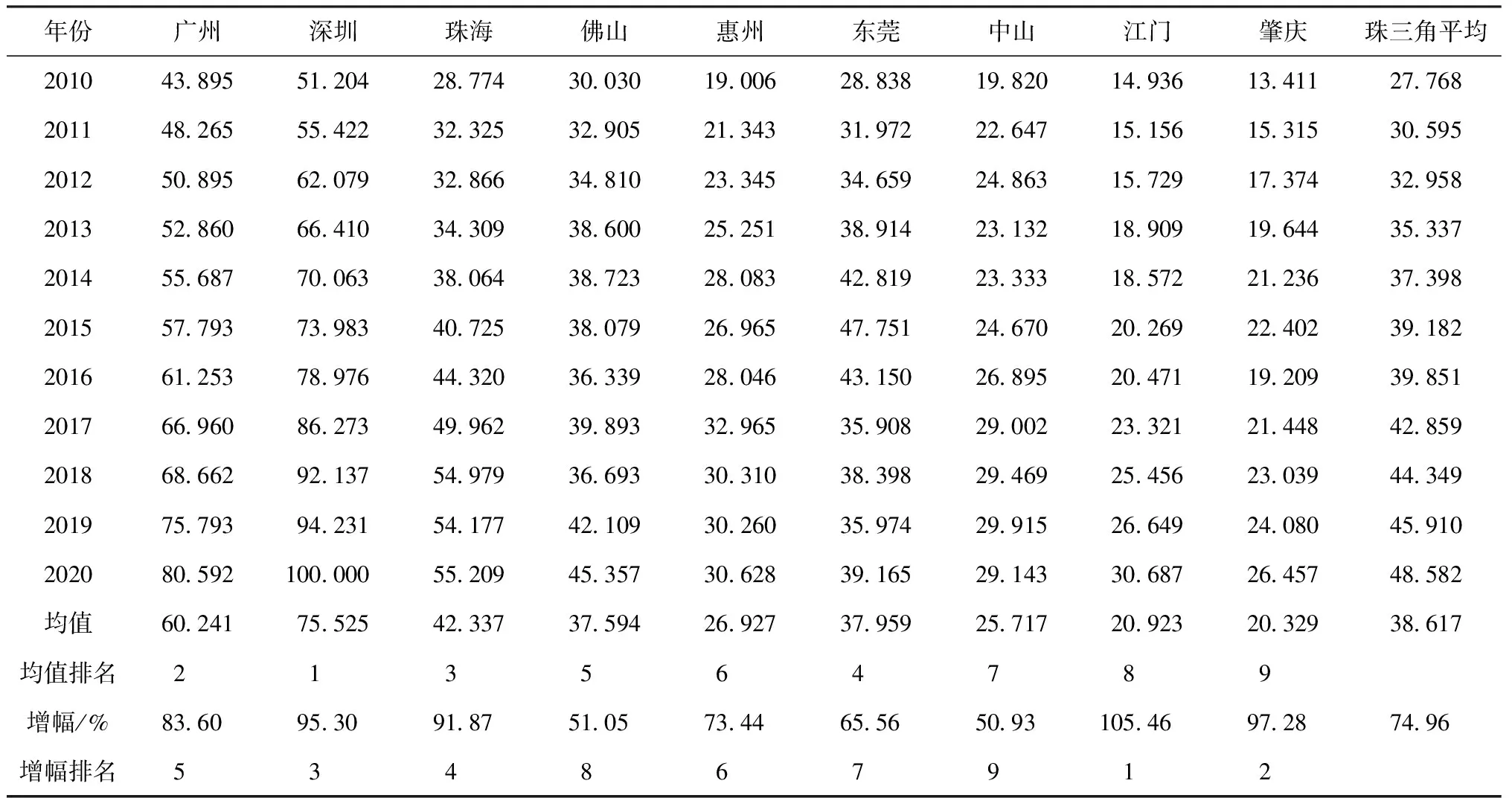
表2 2010—2020年珠三角高科技人才吸引力综合得分及排名

表3 2010—2020年珠三角高科技人才吸引力细项得分及排名(一级指标)

续表

综合表2与表3的研究结果可发现：第一，从珠三角整体层面来看，高科技人才吸引力得分由2010年的27.768增至2020年的48.582，增幅达74.957%，考察周期内珠三角高科技人才吸引力逐年增长，总体呈大幅上涨趋势，未来仍有巨大提升潜力。第二，从细分指标来看，除生活环境状况外，其余各项一级指标得分均较起始考察年份(2010年)有所提升，整体向好。具体来看，各项一级指标得分均值由高至低依次为：自然环境状况(67.905)、生活环境状况(50.923)、经济发展水平(48.435)、信息共享条件(41.614)、教育培训机会(33.382)、社会保障管理(26.557)、人才市场环境(23.056)、科技创新氛围(22.750)，可见提升生活环境状况，加大社会保障管理与完善人才市场环境，营造区域内良好的科技创新氛围是提升大湾区高科技人才吸引力水平的关键所在。第三，从城市层面来看，样本期内九个城市高科技人才吸引力水平均有不同程度提升，但城市间差异显著。九城的高科技人才吸引力得分均值由高至低依次为：深圳(75.525)、广州(60.241)、珠海(42.337)、东莞(37.959)、佛山(37.594)、惠州(26.927)、中山(25.717)、江门(20.923)、肇庆(20.329)。九城的高科技人才吸引力得分增幅由高至低依次为：江门(105.46%)、肇庆(97.28%)、深圳(95.30%)、珠海(91.87%)、广州(83.60%)、惠州(73.44%)、东莞(65.56%)、佛山(51.05%)、中山(50.93%)。相较之下，人才吸引力水平越高(低)的地区得分增幅越小(大)，表明高科技人才低吸引力水平地区对高水平地区存在追赶趋势。

(二)珠三角高科技人才吸引力区域差距及其分解

为了进一步探讨粤港澳大湾区城市高科技人才吸引力的地区差异，运用Dagum 基尼系数及其分解方法，对2010—2020 年珠三角高科技人才吸引力总体基尼系数进行了计算，并且按照《珠江三角洲地区改革发展规划纲要(2008—2020)》(下称《规划纲要》)中三大都市圈划分，对广佛肇、深莞惠和珠中江三个区域进行分解，测算区域内与区域间的高科技人才吸引力水平差距。

1. 珠三角高科技人才吸引力总体差异

从表4所呈现珠三角总体基尼系数结果来看，2010—2020年，高科技人才吸引力总体差距呈现逐步扩大趋势，在11年间总体基尼系数由0.239上升至0.260，总体增长率达8.787%。2010—2015年吸引力的变动幅度较小，2016年后吸引力差距逐渐拉大，总体基尼系数同比增速加快，并于2015—2016年实现最高增速达6.250%。

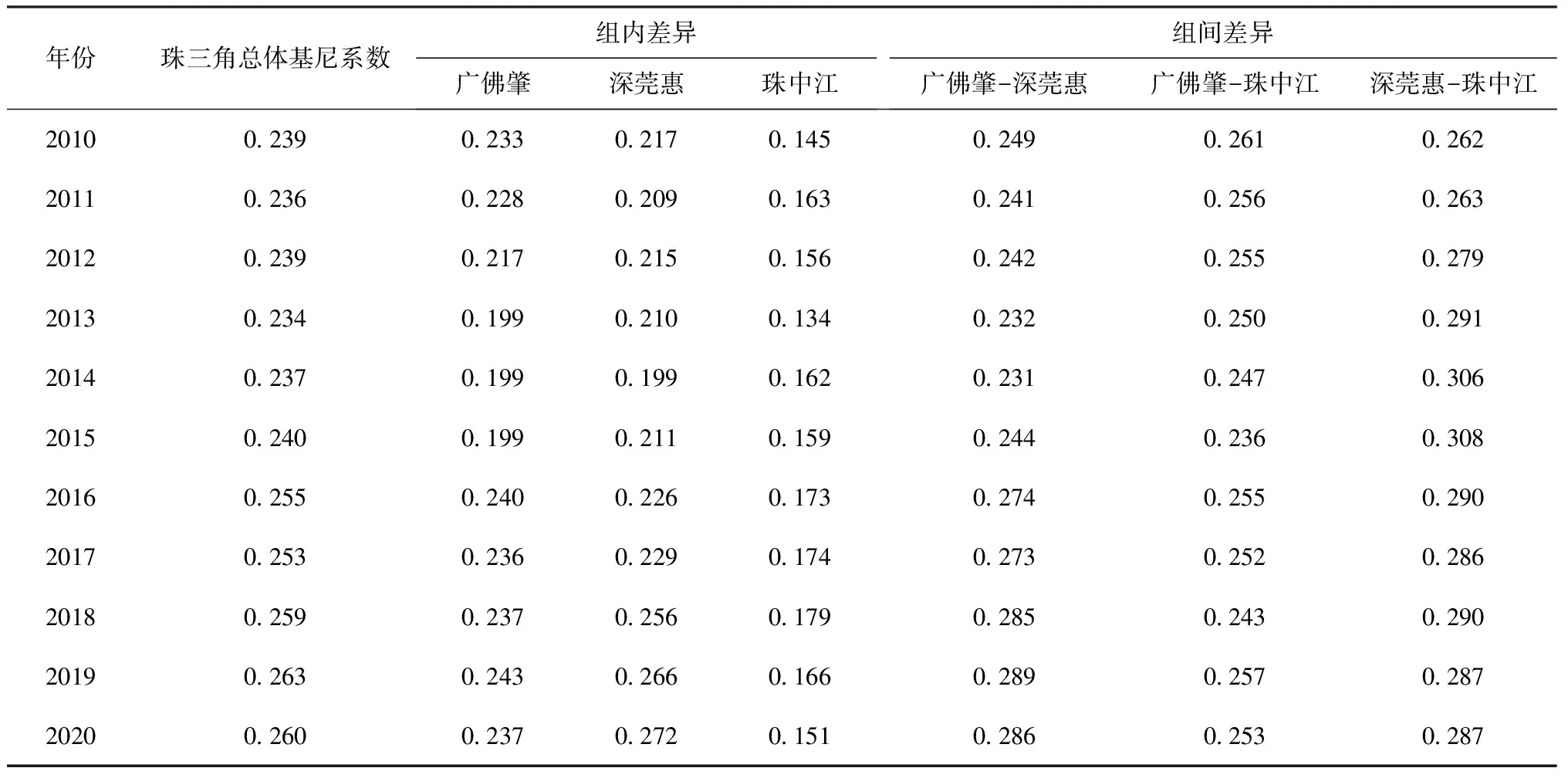
表4 2010—2020年珠三角高科技人才吸引力区域差距及其分解

2. 三大都市圈高科技人才吸引力的组内差异

结合表4数据，对三大都市圈2010—2020年组内差异变动趋势进行了可视化呈现，具体如图2。

广佛肇都市圈的组内高科技人才吸引力差距变动最小，总体波动幅度不超过0.050。考察期内其组内差距经历“缩小—稳定—扩大—稳定”四大阶段。深莞惠都市圈的组内高科技人才吸引力差距变动最大，总体波动幅度达0.073；从发展趋势看，其组内吸引力差距总体上呈先缩小后扩大的态势，相应基尼系数也呈“U”形变动趋势。珠中江都市圈的组内高科技人才吸引力差距变动也相对较小，总体波动幅度以0.001的微弱差距略高于广佛肇都市圈。考察期内其组内吸引力差距经历“扩大—缩小—扩大—缩小”四大阶段。

横向对比来看，珠中江都市圈的组内高科技人才吸引力不平衡性远低于其他两大都市圈，其历年组内基尼系数均远低于其余两组。此外，考察期起始与结束年份的数值对比结果表明，三大都市圈组内高科技人才吸引力差距均呈现扩大趋势，特别是深莞惠都市圈组内吸引力不平等日益加剧。因此，在建设粤港澳大湾区高水平人才高地进程中，要统筹兼顾区域内部高科技人才吸引力的协调发展。

3. 三大都市圈高科技人才吸引力的组间差异

结合表4数据，三大都市圈两两构成三对组间差异。本文对三大都市圈2010—2020年组间差异的演变趋势进行了绘制，具体如图3所示。

广佛肇-深莞惠都市圈在起始年份吸引力组间差距最小，相应组间基尼系数为0.249；从11年的变动趋势来看，组间高科技人才吸引力差距先缩小后扩大。广佛肇-珠中江都市圈组间吸引力差距变动范围最小，其最大组间差距于初始年份即2010年便已达到，相应取值为0.261；从发展趋势来看，2010—2020年组间高科技人才吸引力差距先缩小后震荡扩大。与其他两对都市圈组间差距变动趋势不同，深莞惠-珠中江都市圈高科技人才吸引力的组间差距经历“扩大—缩小—稳定”三大阶段。

图2 三大都市圈组内基尼系数差距

图3 三大都市圈组间基尼系数差距

横向对比来看，在三对组间差距中，深莞惠-珠中江都市圈的组间高科技人才吸引力不平衡性明显高于其他两对都市圈，除2019年，其历年组间基尼系数均高于其余两对。此外，珠三角三大都市圈组间吸引力差距呈现不断扩大趋势，特别是广佛肇-深莞惠都市圈组间吸引力不平等性随时间推移而加剧。这表明各都市圈在高科技人才吸引力方面仍存在较为明显的区域间差异，且这一差距并未随经济社会的发展而趋于平衡。

4. 三大都市圈高科技人才吸引力差异的贡献

为进一步揭示粤港澳大湾区高科技人才吸引力差距的原因，本文对三大都市圈的组内差距Gw、组间差距Gnb及超变密度Gt的贡献值及其贡献率进行测算，结果如表5所示。考察期内三者平均贡献率为28.250%、40.593%及31.157%，故造成三大都市圈吸引力差异的影响因素依次为组间差距、超变密度与组内差距，组间不平等为造成高科技人才吸引力差异的最主要因素。

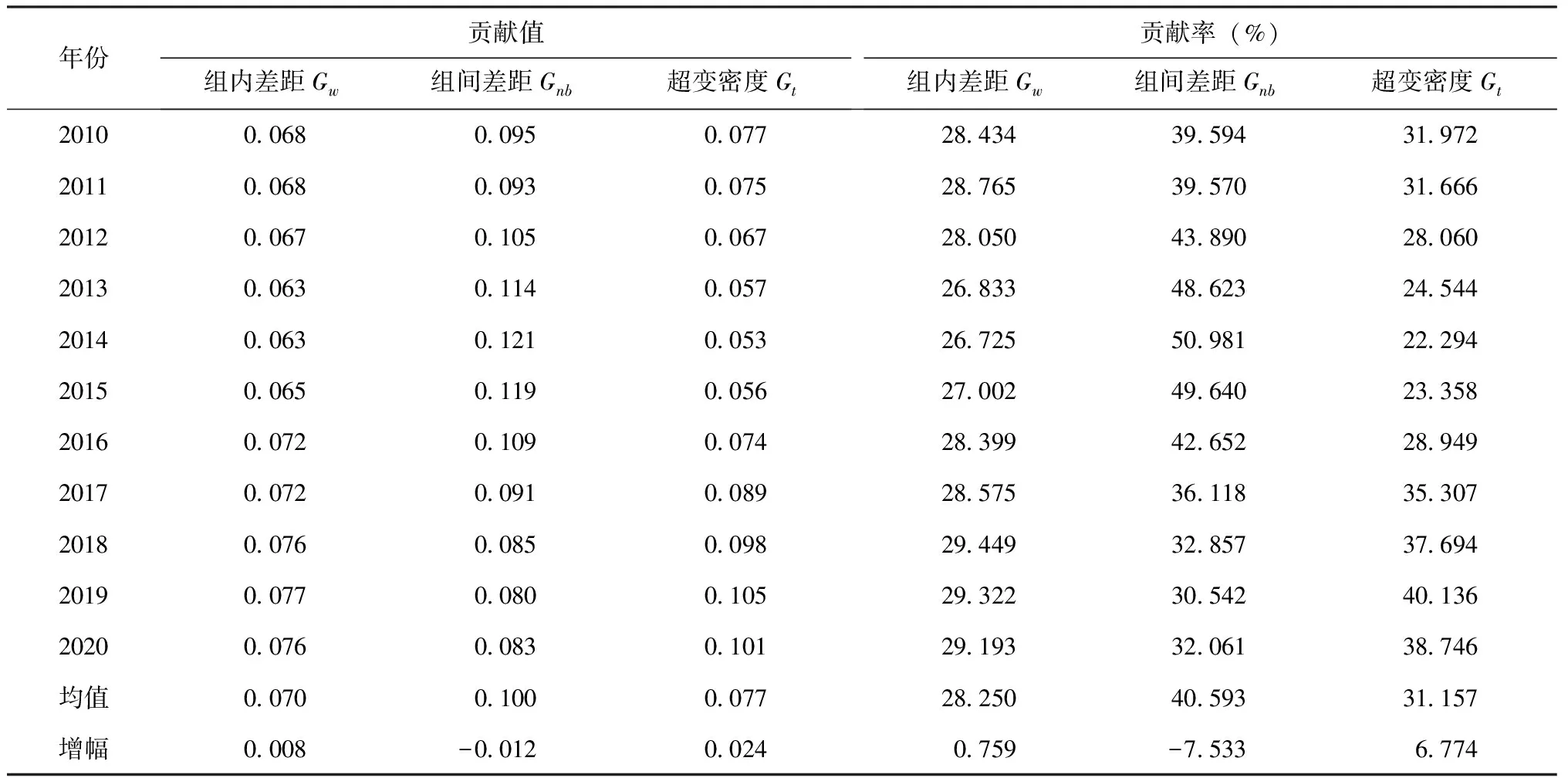
表5 2010—2020年珠三角高科技人才吸引力区域差距来源分解

从各项指标的贡献率来看，三大都市圈组内差距贡献率整体变动较为平缓，保持在28.250%的贡献率水平上下波动。三大都市圈组间差距贡献率则呈先升后降的倒U形趋势，并于该期间始终为珠三角高科技人才吸引力差异的最主要因素。鉴于组间差距贡献率与超变密度贡献率的互补关系，三大都市圈超变密度贡献率于考察期呈先降后升的U形趋势，并于2018年超过组间差距贡献率，成为影响珠三角高科技人才吸引力区域差异的最主要因素。

由此可得出三点结论：第一，对三大都市圈自身而言，其内部吸引力水平差距在11年间始终维持稳定水平，各地对高科技人才的吸引力同步增长或同步衰退；第二，在前期组间差距始终作为珠三角吸引力差异的最主要因素，表明考察期内各都市圈之间高科技人才吸引力差距较大，地区间发展不平衡，人才吸引力极可能并不存在显著收敛现象；第三，在后期，用于识别与衡量组间发展交叉重叠程度的超变密度贡献成为新阶段的主要来源，意味着不同都市圈间交叉重叠问题是造成珠三角高科技人才吸引力不均衡的主要原因。

(三)珠三角高科技人才吸引力的时间动态演进

上文对珠三角三大都市圈高科技人才吸引力的相对组内差异、相对组间差异及来源贡献进行刻画，而对于吸引力绝对差异的分布动态与延展性、极化性演进规律则可借助Kernel密度估计法进行描绘。同样，除了对珠三角总体进行描绘，本文也将按三大都市圈划分，分别对其高科技人才吸引力核密度分布进行描绘，其动态演变特征概括如表6所示。

表6 珠三角及珠三角三大经济圈高科技人才吸引力动态演变特征

1. 珠三角高科技人才吸引力时间动态演进

珠三角城市高科技人才吸引力核密度分布如图4所示。从分布曲线形态来看，珠三角人才吸引力有所上升，且城市间吸引力绝对差异有所缩小。从分布曲线延展性来看，珠三角内吸引力高水平城市数量逐渐增多，低水平城市数量逐渐减少。从分布曲线极化性来看，珠三角吸引力出现初步的两极分化。

2. 广佛肇都市圈高科技人才吸引力水平的时间动态演进

广佛肇都市圈高科技人才吸引力核密度分布如图5所示。从分布曲线形态来看，都市圈吸引力略有下降，但降幅不大，城市间吸引力差距不断减小。从分布曲线延展性来看，圈内吸引力高水平城市与低水平城市比例总体保持不变。从分布曲线极化性来看，单极化现象持续存在。

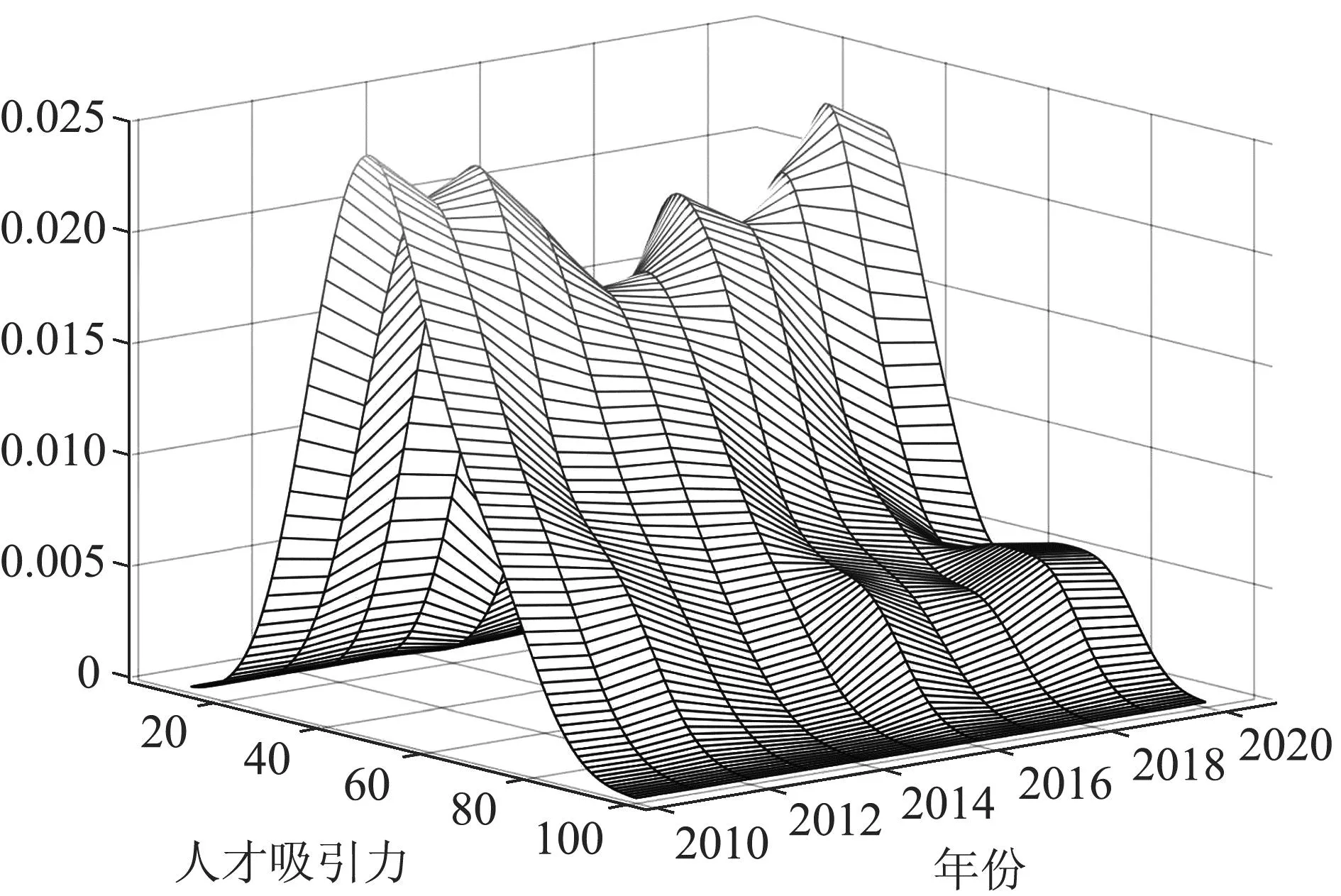
图4 珠三角城市高科技人才吸引力核密度分布

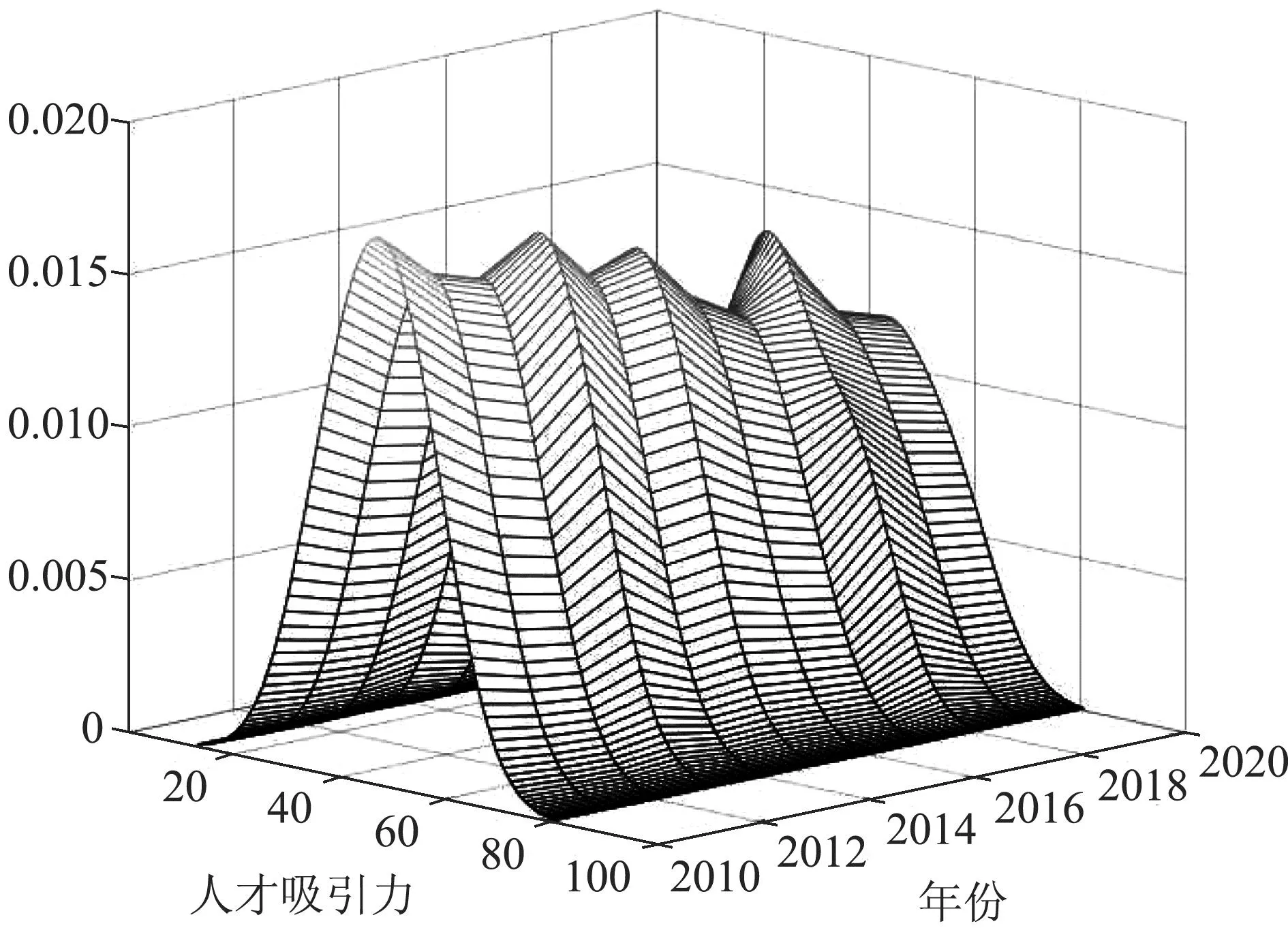
图5 广佛肇都市圈高科技人才吸引力核密度分布

3. 深莞惠都市圈高科技人才吸引力水平的时间动态演进

深莞惠都市圈高科技人才吸引力核密度分布如图6所示。从分布曲线形态来看，都市圈吸引力呈小幅提升态势，城市间吸引力绝对差异仍保持扩大态势。从分布曲线延展性来看，圈内吸引力高水平与低水平城市比例总体保持不变。从分布曲线极化性来看，深莞惠都市圈吸引力具有显著梯度效应，呈两级分化趋势。

4. 珠中江都市圈高科技人才吸引力水平的时间动态演进

珠中江都市圈高科技人才吸引力核密度分布如图7所示。从分布曲线形态来看，都市圈吸引力呈下降态势，扩大态势为圈内吸引力绝对差异的变动态势。从分布曲线延展性来看，圈内吸引力高水平与低水平城市比例总体保持不变。从分布曲线极化性来看，其都市圈人才吸引力变动情形与深莞惠都市圈一致。

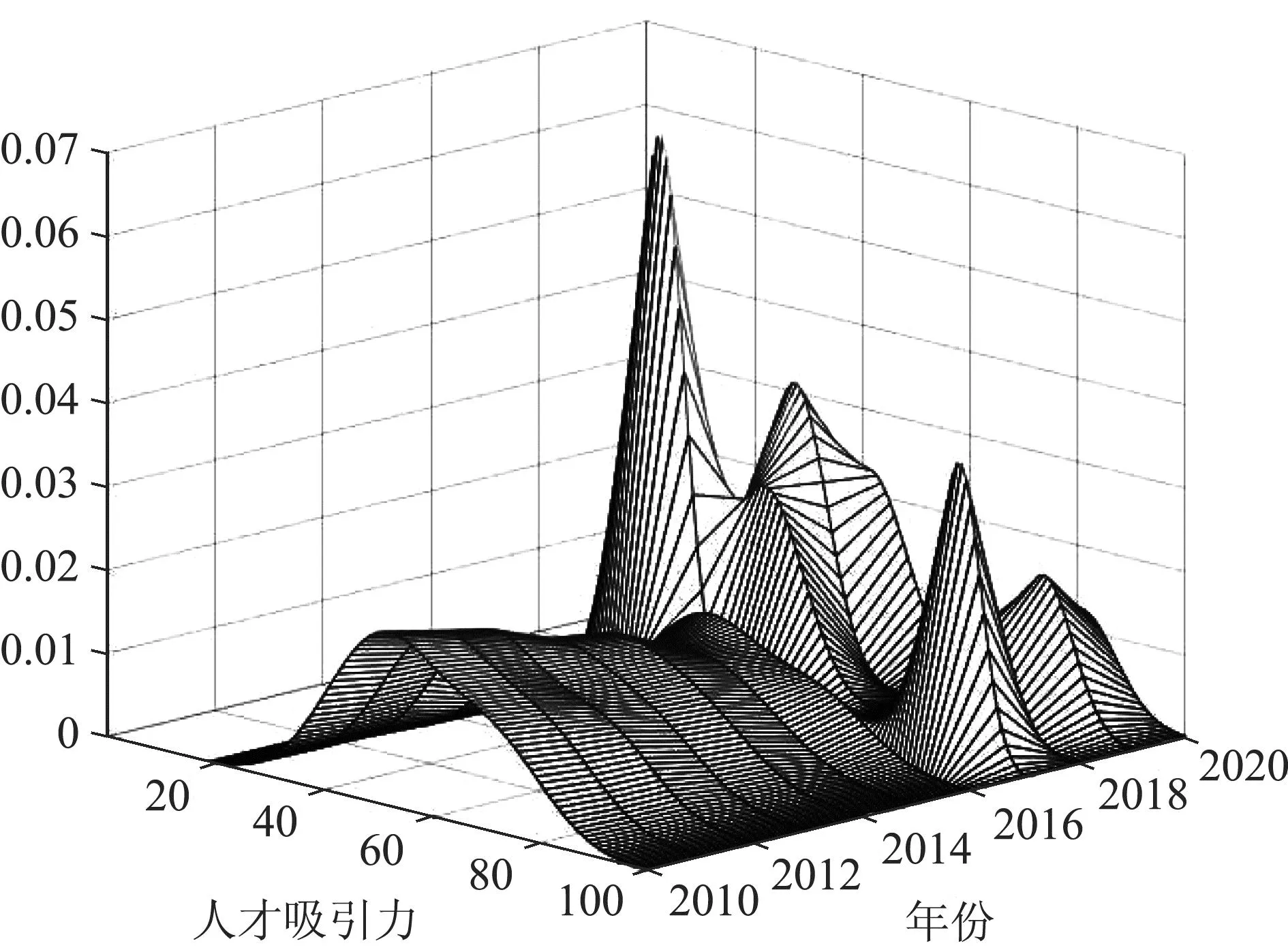
图6 深莞惠都市圈高科技人才吸引力核密度分布

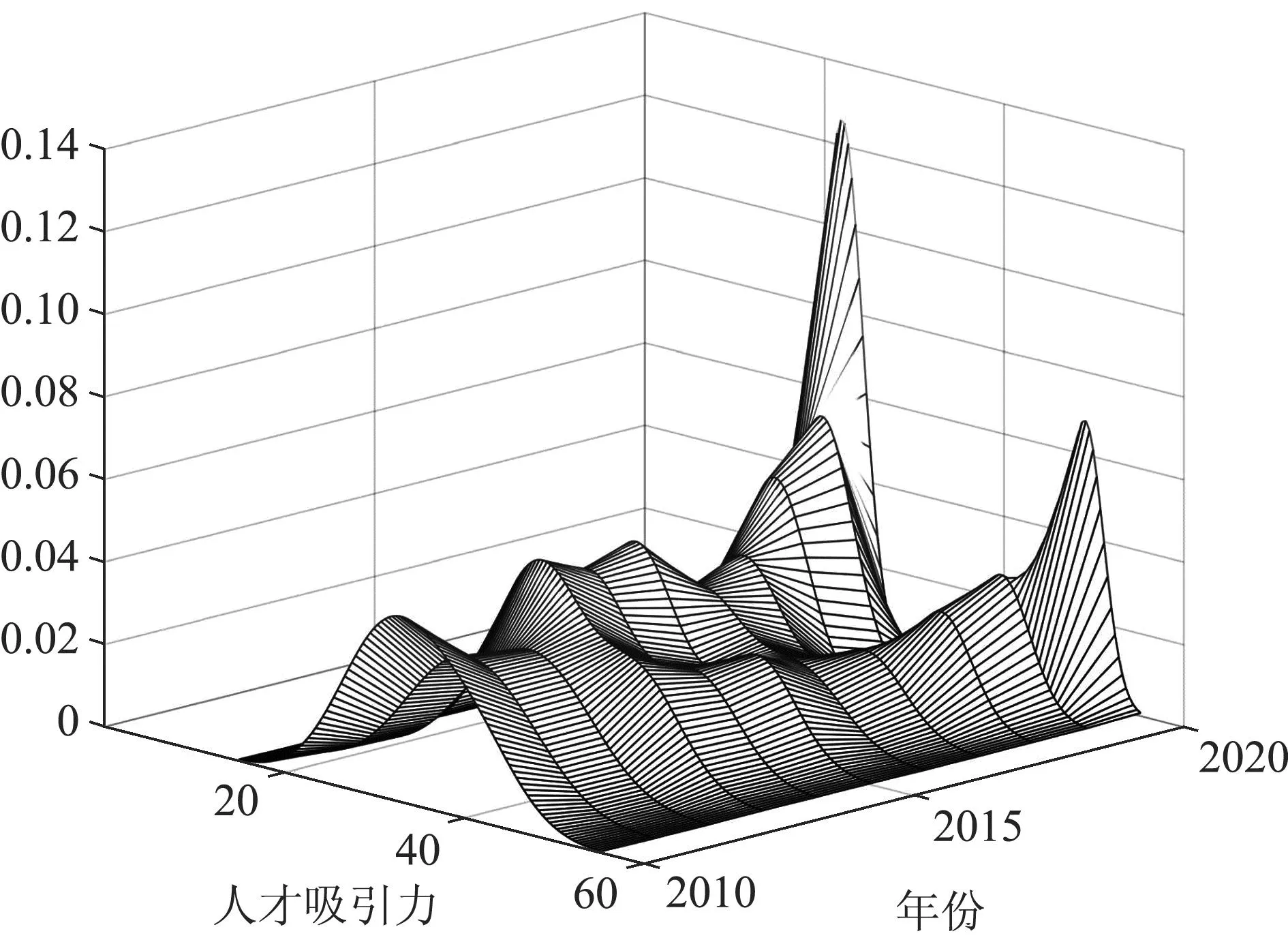
图7 珠中江都市圈高科技人才吸引力核密度分布

(四)珠三角高科技人才吸引力的收敛机制分析

为进一步揭示高科技人才吸引力收敛性机制，本文运用新古典增长模型中的σ收敛和β收敛理论对珠三角及三大都市圈吸引力收敛性进行检验。

1.σ收敛检验

利用σ收敛模型对珠三角及珠三角三大都市圈高科技人才吸引力进行测算，测算结果如图8所示。从珠三角地区测算结果来看，2010—2013年σ收敛系数处于小幅下降期，相应变异系数由0.433下降至0.431；2013—2020年σ收敛系数则处于波动上升期，2020年σ收敛系数达0.447，较2010年上升3.195%。这表明珠三角地区吸引力并未呈现σ收敛，存在一定的发散倾向，即整体来看珠三角高科技人才吸引力地区差异有小幅扩大趋势。

图8 珠三角及珠三角三大都市圈高科技人才吸引σ收敛演变趋势

截至2020年，广佛肇都市圈σ收敛系数为0.455，较2010年数值下降8.01%。这表明其都市圈吸引力呈现σ收敛特征，即广佛肇都市圈吸引力地区差异有所缩小。深莞惠都市圈σ收敛系数于2020年达0.510，较2010年数值增长25.48%。这表明其吸引力呈明显的σ发散特征，即近年来深莞惠都市圈吸引力地区不平衡性日益加剧。珠中江都市圈σ收敛系数在考察期内呈M形变动趋势，但2020年数值较2010年仍小幅增长7.91%。这表明其吸引力具有σ发散特征，即珠中江都市圈吸引力地区差异存在扩大趋势。

总体来看，σ收敛与前文Dagum基尼系数和Kernel核密度估计结果较为一致，表明广佛肇都市圈高科技人才吸引力地区不平等性逐步缩小，呈现σ收敛特征，而珠三角整体区域及深莞惠与珠中江都市圈高科技人才吸引力不平等性日趋扩大，存在σ发散特征。

2. 绝对β收敛检验

首先采取固定效应模型与随机效应模型进行参数估计，Hausman检验结果显示卡方统计量在1%的显著性水平下拒绝“接受随机效应”的原假设，固定效应模型优于随机效应模型。通过构建年份虚拟变量，发现年份虚拟变量联合显著性未通过检验，无法显著拒绝“无时间效应”的原假设。基于此，本文构建个体固定效应最小虚拟变量二乘法(LSDV)模型，以此作为绝对β收敛检验的参数估计基准。此外，为了进一步研究不同维度中高科技人才吸引力的收敛情况，除对吸引力总得分进行绝对β收敛检验，还对八项一级指标得分进行绝对β收敛检验，回归结果如表7 所示。

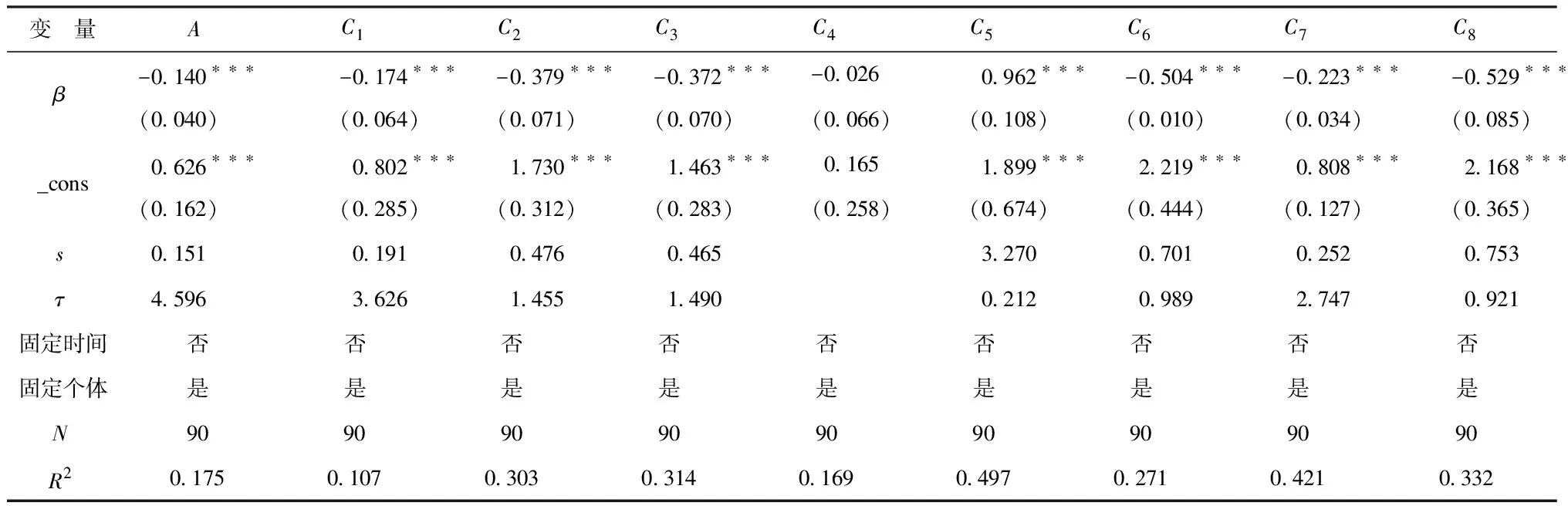
表7 2010—2020年绝对β收敛情况

由表7可得，珠三角高科技人才吸引力绝对β收敛系数为负且通过1%显著性检验，表明珠三角吸引力差距存在绝对β收敛，即当前低吸引力城市发挥了其对高吸引力城市的“追赶效应”，随时间推移高吸引力与低吸引力城市对高科技人才的吸引力差距将收敛于恒定稳态水平，这与珠三角九市高科技人才吸引力综合得分增速结果一致。一级指标检验结果表明，除人才市场环境外，其余七项指标的绝对β收敛系数均显著为负，这表明珠三角在该七项细分领域也存在绝对β收敛，即当前低水平城市通过提升经济发展水平、自然环境状况、生活环境状况、教育培训机会、科技创新氛围、信息共享条件及社会保障管理领域的增长速率以实现高科技人才吸引力差距的稳态收敛。此外，从收敛速度s以及半生命周期τ来看，珠三角地区吸引力收敛速度为0.151，半生命周期为4.596。横向对比八项一级指标收敛速度及半生命周期，社会保障管理收敛速度最快为3.270，相应半生命周期最短为0.212年；经济发展水平收敛速度最慢为0.191，相应半生命周期最长为3.626年。

3. 条件β收敛检验

绝对β收敛假定珠三角城市为空间中性，而条件β收敛则认为不同城市会受到外界因素的不同影响，故对珠三角高科技人才吸引力进行条件β收敛检验时需对相关的控制变量进行设置。参考已有文献，本文设置的控制变量为：

城市人口规模(popu)。城市人口规模引起的经济集聚与拥挤效应共同作用于所有个体，而高科技人才是否向城市集聚则取决于经济集聚效应与拥挤效应的大小。城市面积与城市人口密度均被用于衡量城市人口规模，但城市人口密度更能反映拥挤效应的大小，使用范围更广[32]。借鉴扈爽等[33]的做法，本文采用城市人口密度指标以衡量城市人口规模。

城市金融环境(fin)。良好的城市金融环境通过为人才安居创业与企业扩大经营规模提供便捷高效、成本低廉与需求适配的借贷服务，从直接与间接层面影响高科技人才向城市集聚[34]。借鉴方芳等[35]的做法，本文采用年末金融机构存贷款余额衡量城市金融环境。

城市法治环境(law)。良好的城市法治环境通过保障人才个人劳工权益与企业知识产权，营造社会良性就业氛围与企业竞争环境，同样从直接与间接层面影响城市对高科技人才的吸引力[34，36]。本文在借鉴孙博等[31]的做法之余，考虑数据可得性，采用法院案件一审结案率衡量城市法治环境。

同样地，本文构建个体固定效应LSDV模型，以此作为条件β收敛检验的参数估计基准，对高科技人才吸引力总得分进行条件β收敛检验，回归结果如表8所示。

表8 2010—2020年条件β收敛情况

由表8可知，珠三角高科技人才吸引力条件β收敛系数为负且通过1%显著性检验，表明在考虑城市人口规模、金融环境与法治环境因素，固定城市个体的情况下，珠三角吸引力呈现条件收敛特征。此外，对比绝对收敛与条件收敛的收敛系数，后者收敛系数绝对值更大，相应的收敛速度与半生命周期也有所提升，表明控制变量的加入，对缩小湾区吸引力差距产生促进作用。未来粤港澳大湾区可通过控制区域人口规模、改革金融环境、优化法治环境加速来改变湾区高科技人才吸引力不平衡现象。

四、稳健性检验及进一步研究

(一)Dagum基尼系数的稳定性检验

图9 2010—2020年珠三角及珠三角三大都市圈泰尔指数测度结果

同样作为刻画区域非均衡性指标，泰尔指数也通过计算组内差异与组间差异实现对区域总体差异的分解。故本文采用泰尔指数测度珠三角及三大都市圈高科技人才吸引力的非均衡性，以期检验前文Dagum基尼系数结论。但考虑到泰尔指数在处理样本间交叠问题存在缺失，在此仅对珠三角总体泰尔指数与各都市圈组内泰尔指数变动趋势进行对比。2010—2020年珠三角及珠三角三大都市圈泰尔指数测度结果如图9所示。

对比图2与图9，不难看出无论在珠三角总体层面，还是在广佛肇、深莞惠及珠中江三大都市圈层面，泰尔指数的变动趋势均与Dagum基尼系数结果保持一致，表明本文使用Dagum基尼系数对高科技人才吸引力区域差距进行衡量的测度结果基本稳定。

(二)空间计量下的β收敛检验

β收敛检验以样本间相互独立为检验前提，然而随着高科技人才吸引力指标要素流动日趋频繁，样本间可能出现除地理因素外的空间经济依赖性[32]。对2010—2020年珠三角九市高科技人才吸引力水平空间依赖性进行验证，全局莫兰指数在统计意义上显著且小于0，表明高科技人才吸引力水平存在空间相关性。基于此，本文进一步使用空间β收敛检验对空间分布加以考虑。

基于无空间交互项的OLS模型残差进行LM检验，结果表明R-LM-lag显著优于R-LM-err。进一步的利用LR统计量与wald统计量对空间杜宾模型(SDM)的适用性进行检验，检验结果不能拒绝原假设，不支持选择SDM模型。Husman检验拒绝原假设，纳入固定效应模型分析。因此，本文基于空间滞后回归模型(SRA)，设定高科技人才吸引力水平的空间绝对β收敛模型和空间条件β收敛模型如式(29)和式(30)所示。

(29)

(30)

式中，ρ为空间自回归系数，用于反映高科技人才吸引力的空间关联性，即相邻区域的人才吸引力水平对本地区人才吸引力水平的影响；Wij为空间权重矩阵。

为了对高科技人才吸引力的空间关联特征予以系统考察，本文分别构建了地理空间权重矩阵与经济地理空间权重矩阵。

地理空间权重矩阵：

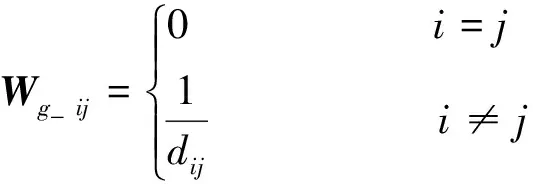
(31)

式中，dij为城市i与城市j之间的地理距离(dij>0)，本文使用地级市间行政中心的最短公路线网里程进行衡量。

经济地理空间权重矩阵：

(32)

eij=|pGDPi-pGDPj|

(33)

式中，eij为城市i与城市j之间的经济地理距离，本文使用2010—2020年城市i与城市j人均GDP均值的差值绝对值进行衡量。

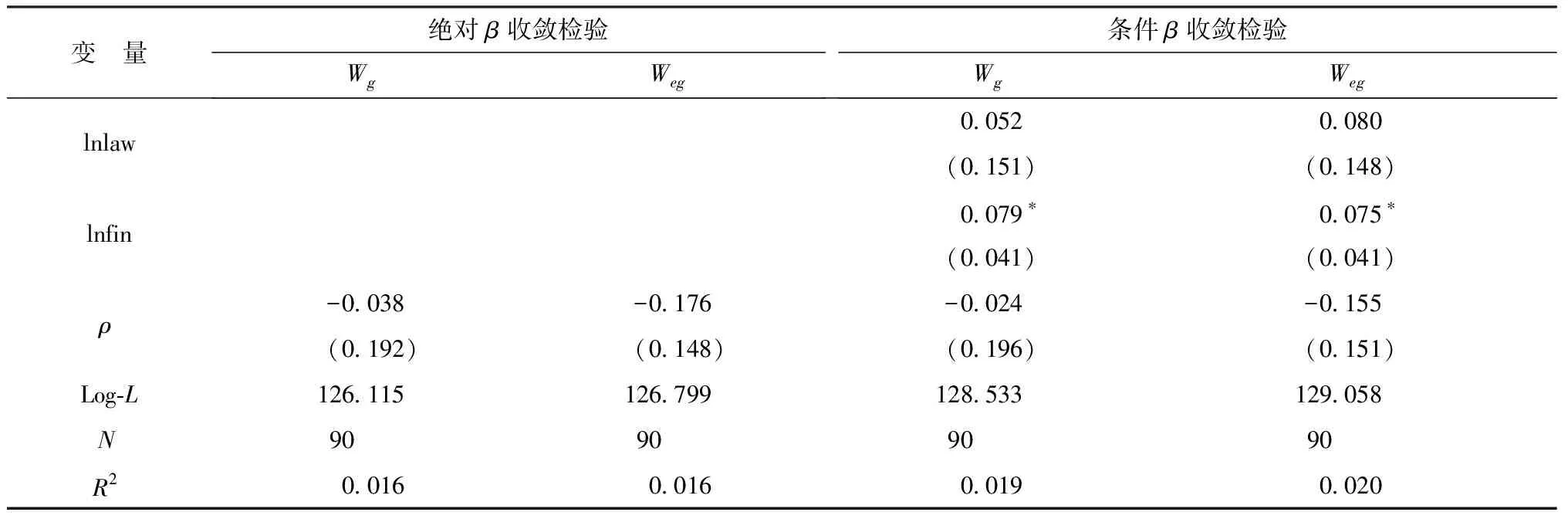
2010—2020年珠三角高科技人才吸引力空间绝对β收敛结果与空间条件β收敛结果如表9和表10所示。从表9与表10的结果来看，高科技人才吸引力总得分空间绝对β收敛系数与空间条件β收敛系数均在1%的水平下显著为负；除人才市场环境一级指标外，其余七项一级指标的空间绝对β收敛系数也均显著为负。基本计量分析结果并未发生改变，表明前文所阐述的β收敛机制具备较高的稳健性。

表9 2010—2020年珠三角高科技人才吸引力空间β收敛结果

续表

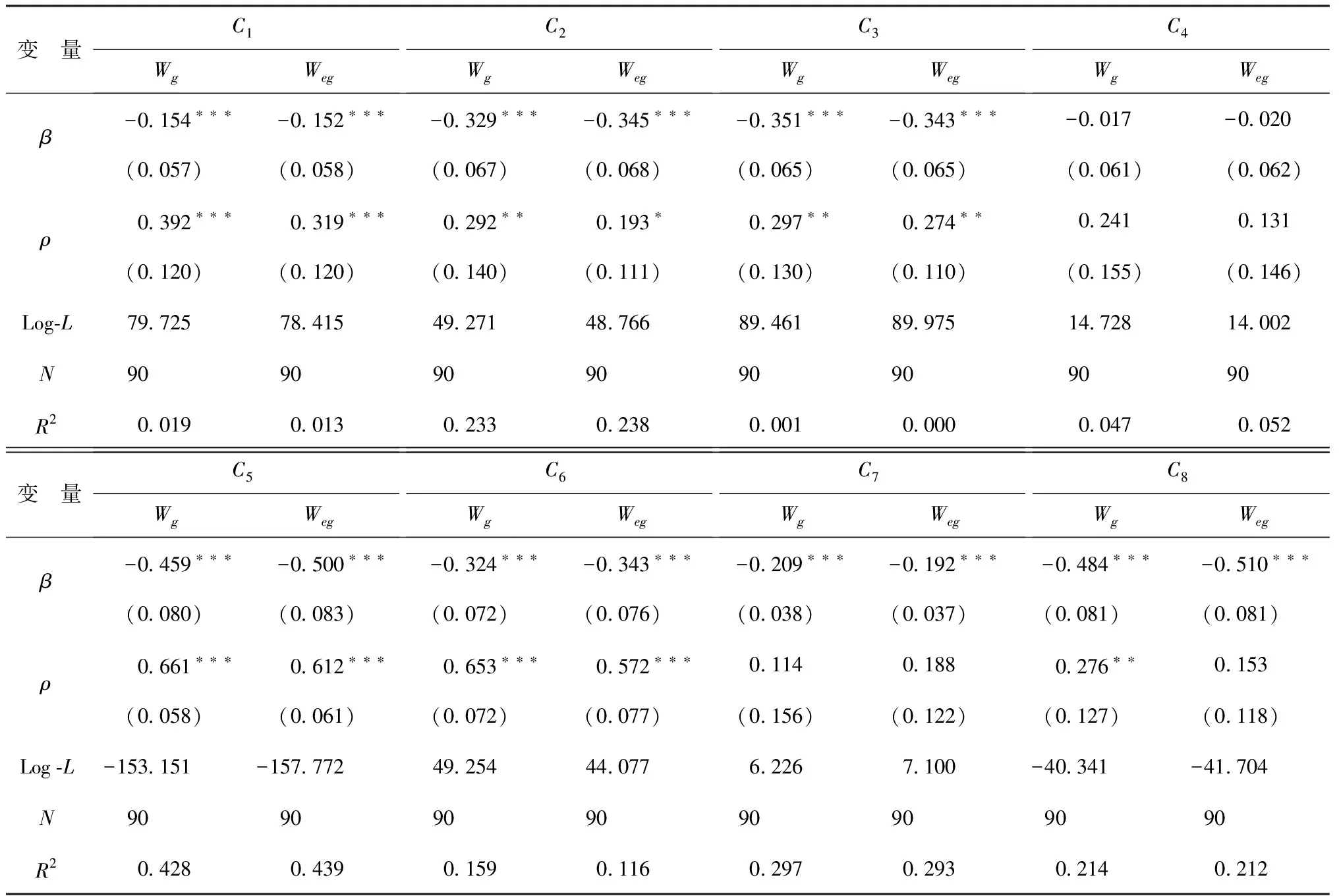
表10 2010—2020年珠三角高科技人才吸引力各分项空间绝对β收敛结果

(三)基于ASDNTY的俱乐部收敛

鉴于2010年之前所选取的二级指标统计数值存在时空的不连续性与缺失，致使本文对研究年份的选取局限于2010—2020年，所能计算的样本数据量受限。对此，本文借鉴刘逸等[33]的处理方法，使用自适应综合过采样算法(ADASYN)扩大样本容量，以进行俱乐部收敛检验。

ADASYN的算法原理是以样本数据集的密度分布为标准，自动确定需平衡样本的适宜权重，并为处理样本生成相应数量的合成样本，最终构造模拟样本集以丰富原始样本集[34]。本文通过利用ADASYN算法，依次对珠三角中的一个城市与其余八个城市的数据进行数据样本平衡处理，利用少数类样本的原始信息拟合趋近于真实高科技人才吸引力的模拟样本，总计将数据量由99条提升至765条。

同样依据《规划纲要》中的三大都市圈划分，本文将广佛肇、珠中江和深莞惠都市圈视为三类发展俱乐部，同样采取个体固定效应LSDV模型对其高科技人才吸引力水平进行俱乐部收敛检验，结果如表11所示。

对比表7和表11检验结果，ADASYN算法处理前后，珠三角总体回归结果均在1%的统计性水平下显著为负，回归系数相差不大，表明新生成的模拟样本具有一定的稳健性。此外，从俱乐部检验结果来看，广佛肇、珠中江和深莞惠都市圈β收敛系数均显著为负，这表明三大都市圈吸引力均呈现显著收敛特征，具备俱乐部收敛机制。从收敛速度s以及半生命周期τ来看，深莞惠俱乐部收敛速度最快为0.323，相应半生命周期最短为2.146年；广佛肇俱乐部收敛速度次之为0.268，相应半生命周期为2.588年；珠中江俱乐部收敛速度最慢为0.247，相应半生命周期最长为2.804年。

五、结论与建议

本文通过对2010—2020年珠三角地区高科技人才吸引力水平进行定量测度，借助Dagum基尼系数与Kernel核密度函数对珠三角高科技人才吸引力区域空间差异机理及动态演进规律予以描绘，并运用σ收敛与β收敛模型对吸引力空间收敛性进行特征分析，最后借助空间β收敛模型及ADASYN算法对模型进行稳健性检验与拓展分析。主要结论为：

第一，高科技人才吸引力呈向好发展态势。2010—2020年珠三角高科技人才吸引力逐年增长，总体呈大幅上涨趋势。第二，高科技人才吸引力空间相对不平衡性特征显著，珠三角吸引力空间相对差距呈逐步扩大趋势。第三，高科技人才吸引力空间绝对不平衡性略微缩小。第四，高科技人才吸引力存量收敛性不显著，增量收敛性特征显著。

为提高粤港澳大湾区城市高科技人才吸引力与区域协调发展，本文基于上述研究结论提出以下建议：

第一，补齐发展短板，打造粤港澳大湾区高科技人才高地。从本文构建的吸引力指标体系中各项指标的变动态势及相对得分来看，生活环境状况的改善，人才市场环境的规范与科技创新氛围的营造应被作为未来一段时间内大湾区提升高科技人才吸引力的工作重点。改善生活环境状况是吸引力提升的重中之重，需进一步在住房、医疗、交通领域保障人才基本生活需求，防止“人才挤出”现象的发生，使人才在湾区安身、安心、安业。在人才市场环境方面，要遵循高科技人才的培养与科研规律，破除“四唯”倾向的管理机制障碍；在经费支配、资源调度与技术路线上赋予人才更高的自主决策权，做到以人才为本，为人才松绑。在科技创新氛围方面，积极培育建设一大批国家实验室、大型系列研究平台、高水平研究型大学、科技领军企业等创新机构，支持高科技人才紧跟当前全球科技发展大势，对标世界一流水平，让事业激励人才，让人才成就事业。

第二，发挥比较优势，实施补短板铸长板并重的战略方针。基于粤港澳大湾区高科技人才吸引力时空分布不均的空间特征，因地制宜地对不同吸引力水平区域分类施策。广州市与深圳市作为高吸引力地区，应强化其经济发展与市场化长板优势，持续深化简政放权、放管结合，充分发挥市场在资源配置中的决定性作用；提升生活环境短板劣势，加大对高科技人才住房、交通及医疗等补贴投入，解决人才日常生活难题。珠海市、佛山市与东莞市作为中吸引力地区，应找准其支柱产业，发挥长板优势，注重与现有优势产业相匹配的专项高科技人才吸引，找准特色人才吸引力定位；挖掘本地盲区短板劣势，优化人才吸引的软硬件条件。惠州市、中山市、江门市与肇庆市作为低吸引力地区，应发挥人居环境长板优势，通过加强城市宜居性，以较低成本聚拢高科技人才；正视产业落后等短板劣势，发挥政府职能主导作用，利用政策手段加快本地落后产业转型升级，借助供给侧结构性改革吸引人才流入。

第三，扩大辐射效应，统筹高科技人才吸引力区域协调发展。基于大湾区的高科技人才吸引力空间相对不平衡性与绝对不平衡性特征，广州市、深圳市与珠海市除进一步稳固当前高科技人才吸引力水平外，还应发挥高科技人才的正向知识溢出效应，加大对都市圈内低吸引力城市的扶持力度，发挥引领作用缩小各都市圈组内及组间吸引力差距，统筹兼顾区域人才吸引力协调发展。目前，深圳市通过转移过剩产能，辐射带动圈内其他城市提升高科技人才吸引力已有成效，广州市与珠海市也可借鉴这一方案，以缩小圈内高科技人才吸引力不平等性。此外，粤港澳大湾区各级政府间还应建立联席协商机制，制定人才跨区域流动体制机制，打破行政区间高科技人才流动障碍，实现高科技人才资源跨区域转移优化，以利于区域间优势互补，协同共促高科技人才吸引力提升。

第四，发挥追赶效应，注重收敛速度与发展差距之间的协调性。绝对β收敛检验、条件β收敛检验及俱乐部收敛检验结果均表明，当前区域内低吸引力城市发挥了其对高吸引力城市的“追赶效应”，且随时间推移城市间吸引力差距将收敛于恒定稳态水平。从条件β收敛系数来看，未来粤港澳大湾区的确可进一步通过控制区域人口规模，改革金融环境，优化法治环境，加快低吸引力城市的追赶速度，进而加速缩小地区间高科技人才吸引力不平衡。与此同时，各地政府需树立科学认知：缩小地区间吸引力不平衡的最终目的不是使各城市高科技人才吸引力相等。不同城市对高科技人才的吸引力将收敛于各自的恒定稳态，低吸引力城市不能限于指标陷阱，盲目追赶高吸引力城市以期达到同等吸引力水平，提升本地吸引力收敛速度才是缩小地区间不平等性的关键所在。从各项一级指标的收敛速度来看，在社会保障管理、信息共享与教育培训领域着手施策，将有助于更快提升本地高科技人才吸引力收敛速度。