磁性小口径血管磁-结构耦合理论、仿真分析与测试
刘世海,苗晓丹,陈赫,刘道伟,张子衡
(上海工程技术大学机械与汽车工程学院,上海 201620)
随着社会的不断发展,人们的生活质量也越来越高,由不健康的饮食引起的心血管疾病也日渐成为威胁人类健康的杀手之一.根据世界卫生组织资料显示,心脑血管疾病死亡病人主要在发展中国家之中,2013年发展中国家死亡人数大约占全球死亡人数的80%[1].《中国心血管健康与疾病报告2020》显示,2018年我国冠心病死亡率约为120.18/10万,脑血管病死亡率约为149.49/10万,在所有死亡原因中,恶性肿瘤、心脏病和脑血管病占据了前三位[2].血管疾病的主要治疗手段是血管移植手术,目前,临床主要使用的血管移植物是自体血管及非降解性合成材料管.尽管自体血管替换病变血管的术后效果满意,但却因为自体血管来源有限和供区创伤等原因难以满足临床的大量需求[3];因此,人工血管成为治疗血管疾病的另一种选择.内径在6 mm以上的大口径人造血管已经应用于临床,但内径小于6 mm的小口径人工血管常会造成植入失败,其主要原因是血管管径窄、易栓塞和远期通畅率低[4-5].血管疾病治疗的理想方案是在切除病损部位之后,血管支架能引导组织在原位再生长出血管.一些可降解的人工合成材料PGA[6]、PLA[7]、PCL[8]、PLGA[9]、PLCL[10]以及天然可降解材料丝素蛋白[3]等已被用于血管再生支架的制备.
Roh[11]用PGA纤维网和PCL/PLA混合溶液通过浇注的方法制备了一种内径为0.9 mm的小口径血管支架,之后把PGA纤维网换成PLLA纤维网用相同的方法制备了内径为0.7 mm的小口径血管支架.Uchida[12]用PCL/PLA混合溶液通过盐滤沥法等方法制备了一种弹性模量介于0.6~5.2 Mpa之间的血管支架.Kuwabara等[13]用PCL溶液通过静电纺丝的方法制备了一种可内径为0.7 mm、可置换小鼠主动脉的小口径血管支架.他们所制造的小口径血管支架都有共同的不足:在体外都是以液体为介质来模拟生理脉动,这会使血管受到的剪切力与血管脉动耦合在一起且血管脉动具有一定的滞后性,血管支架本身不能模拟天然血管因为脉动而引起的扩张.一些研究人员[14-18]已经证实了由机械刺激引起的生物力学力可加强工程组织的力学性能,从而通过磁场在磁性血管支架上施加合适的刺激可以加强再生组织的强度以及加快血管细胞的生长.
针对上述问题,本文提出了一种磁性小口血管支架整体方案设计,利用磁性颗粒掺杂的方法,使得人造血管支架在外加磁场作用下能够反复变形,从而形成与天然血管类似的脉动作用,促进其壁上的细胞生长;并且配合生物反应容器可实现血管所受剪切力与脉动的解耦合,为分别研究剪切力和血管脉动对血管细胞生长的影响提供了一种新思路.本文主要研究内容包括:通过对磁性小口径血管的功能属性进行分析,根据静电纺丝工艺,对磁性颗粒掺杂条件下的不同浓度工艺参数进行优化,制备磁性小口径血管支架并进行充磁;建立磁性小口径血管支架与外磁场之间磁-结构耦合作用物理模型并进行理论分析,利用实验与仿真结合的方式进行定量的验证,从而验证磁性小口径血管的可行性.
1 整体方案设计和理论分析
1.1 方案设计和工作原理
本文总体设计方案是基于静电纺丝的方法,在纺丝溶液中掺杂了不同质量的钕铁硼磁性颗粒形成不同质量分数的纺丝溶液来制备小口径血管支架并采用溶液浸泡法使制备完成的血管支架从支撑棒上脱下来.磁性小口径血管支架由于其内部包含钕铁硼磁性颗粒,所以具有硬磁材料特性.硬磁材料必须用较强的外磁场才能使其磁化,在充磁之后不会轻易退磁,即使把外磁场撤去也能在较长时间内保持稳定的磁性.血管支架充磁之后,具有与通电充磁线圈磁极一样的方向,假设电流为逆时针方向,根据右手定则通电线圈上面为N极,下面为S极,则血管支架磁极也是如此,如图1所示.利用同性相斥异性相吸的原理,当永磁体靠近磁性小口径血管支架时,血管支架在外加磁场的作用下被吸引,产生变形;当永磁体远离磁性血管支架的时候,支架受到外加磁场作用变小,恢复到原来的状态;按一定的周期循环,从而模拟天然血管在脉动下的状态;工作原理图如图2所示.
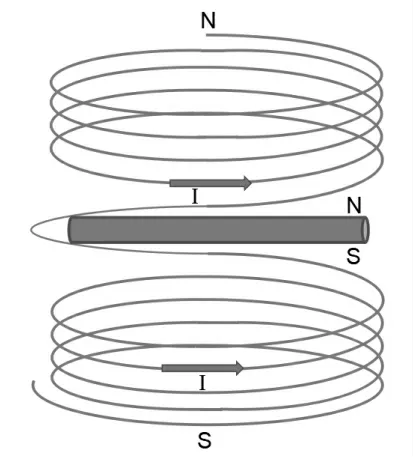
图1 血管支架充磁方向示意Fig.1 Schematic diagram of magnetization direction of vascular stent
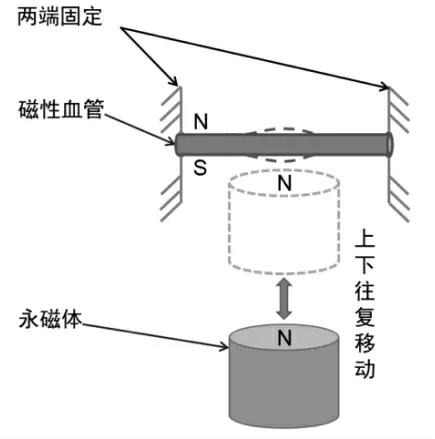
图2 磁性小口径血管支架工作原理Fig.2 Working principle of magnetic small caliber vascular stent
1.2 磁性小口径血管剩余磁化强度计算
以不同质量分数的溶液制备的磁性小口径血管支架其内部所含磁性颗粒数量是不同的,静电纺丝技术制备的血管支架其内部孔隙也有大小之分,这样对于同一性质体积相同的两血管支架在相同的外磁场磁化时,可以有不同的剩余磁化强度.为了使理论分析和仿真分析更精确,本文在此基于半实验验证法对不同质量分数的磁性小口径血管支架充磁之后的磁化强度进行了计算:用VSM先测出血管支架磁滞回线,读出其与y轴交点的数据EMU,再把数据依次代入公式(1)和(2)即可得到剩余磁化强度Mr(emu/cm3),最后再根据等式1 emu/cm3=1 000 A/m计算出所需要单位的剩余磁化强度(A/m).

式(1)、式(2)中:σr为比剩余磁化强度,单位为emu/g;EMU为磁滞回线与y轴交点数据,单位为emu;m为质量,单位为g;Mr为剩余磁化强度,单位为emu/g;ρ为密度,单位为g/cm3.
以质量分数为2.5%的磁性小口径血管支架为例计算其剩余磁化强度,质量分数为2.5%的磁性小口径血管支架磁滞回线如图3所示.2.5%质量分数血管支架样品质量m为2.23mg,密度ρ为7.57g/cm3,磁滞回线与y轴交点读数EMU为0.003 2 emu,根据公式(1)和(2)计算得到其剩余磁化强度Mr为1.435 emu/g,最后换算得到剩余磁化强度M约为1.1×10e4A/m.同理可计算得到4%、5.5%、7%、8.5%质量分数血管支架剩余磁化强度分别为3.4×10e4A/m、5.7×10e4A/m、8×10e4A/m和1.03×10e5A/m.
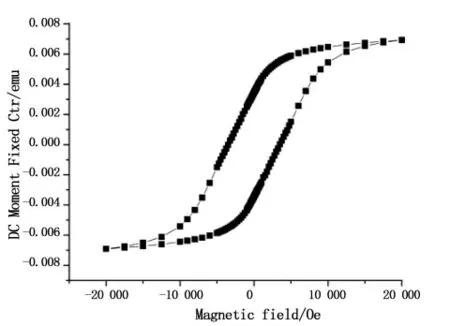
图3 2.5%的磁性小口径血管支架磁滞回线Fig.3 Hysteresis loop of 2.5%magnetic small caliber vascular stent
1.3 磁-结构耦合理论分析
磁性小口径血管支架模拟天然血管脉动主要是通过永磁体在血管支架上施加往复循环的磁场力来实现的.为了对磁性小口径血管支架磁-结构耦合之间的关系进行定性分析,因此需要对永磁体磁场强度、磁感应强度,永磁体对磁性颗粒所施加的磁场力,血管的变形,磁场力与血管变形之间的关系进行理论分析,建立磁-结构之间的关系规律.
1.3.1 永磁体磁场理论分析 根据等效磁荷模型,可以认为均匀充磁的永磁体只有在充磁方向上的两个极面上有正负面磁荷.按照这种模型计算永磁体磁场的公式为[19]
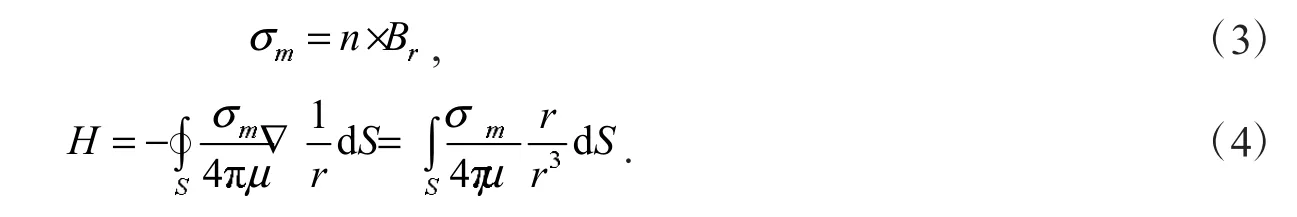
式(3)、式(4)中:Br为剩余磁化强度,n为永磁体边界外法线单位矢量,r为源点与场点之间的距离,S为永磁体边界面,σm面磁荷密度.
在本文中,磁性微粒钕铁硼通过静电纺丝被纺在聚己内酯血管内部,磁性微粒相对于血管来说是固定不动的;带磁性微粒的血管是径向充磁,我们研究的也是血管的径向位移,那么在此我们可忽略在x、y方向上由磁性微粒在外部磁场作用下产生的磁力,只需要考虑z方向上的磁场力即可.这样一来,我们只算Hz.
径向充磁的圆柱形永磁体正负两极都为半圆柱体,正负两个极面都是半圆曲面,为方便计算,可把圆柱体永磁体看成外接四边形的长方形永磁体,如图4所示,这样就把半圆曲面的极面近似等效为长方形极面.建立如图5所示坐标系,由式(4)可得出点P(x,y,z)磁场强度.
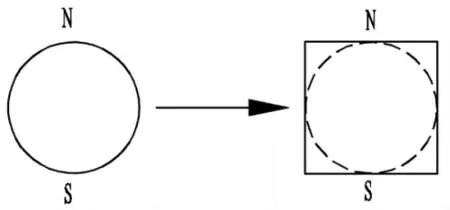
图4 极面等效示意图Fig.4 Equivalent schematic diagram of polar surface
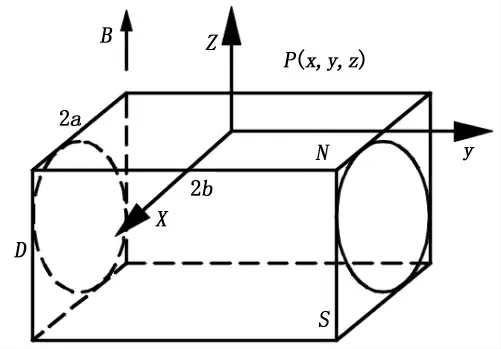
图5 圆柱形永磁体示意Fig.5 Schematic diagram of cylindrical permanent magnet
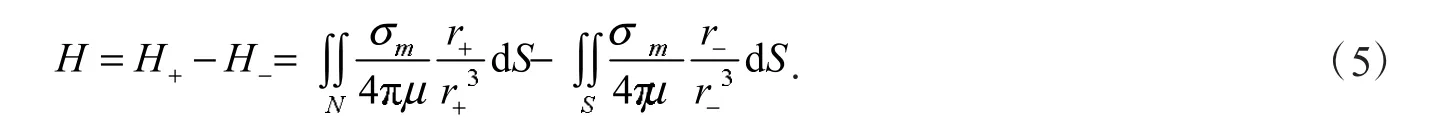
式(5)中:H+,H-,分别为正负磁荷产生用磁场;N,S为产生正负磁荷的源面积;r+,r-,为正负磁荷的源点到场点P的距离.对式(5)中第一项计算有
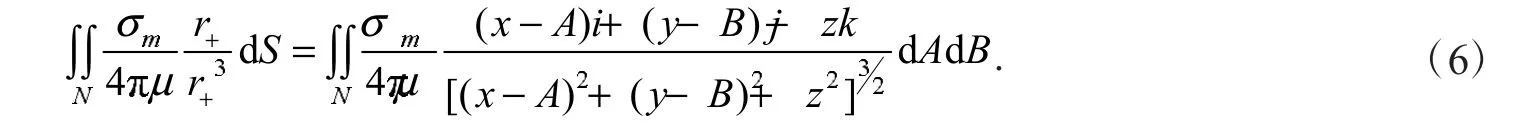
由于积分是对源坐标进行积分,为了避免和P点坐标混淆,用ABC来表示.用HNz表示其在z方向上的分量

同样的,对式(5)中第二项计算有
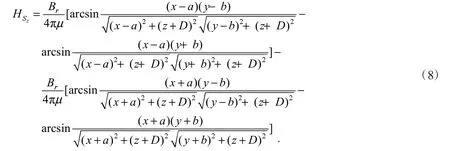
本文研究的是在血管在对称中心轴上这一特殊位置的位移,即P(0,0,z),所以总磁场强度z方向的分量为
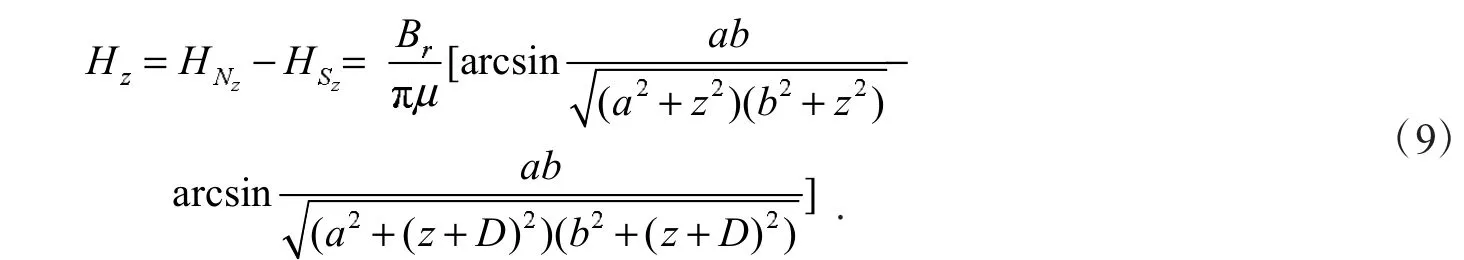
1.3.2 磁性微粒所受磁场力分析 磁性微粒在非均匀磁场中受到的力如图6所示,由于磁性微粒是固定在血管支架内部且其质量很小,其重力可通过血管支架抵消,所以可忽略重力.磁性微粒均匀分布在血管支架中,在此我们分析单个磁性微粒的受力情况,然后把当个磁性微粒所受磁力累加得到整个血管上所受磁力.永磁体所产生的磁场其特点是非均匀的,在磁场范围内,随着空间位置的不同,其方向和大小也会跟随着变化,磁场的这种特性可以用磁场梯度来表示,磁场梯度是一个矢量,它表示为磁场强度在磁场方向上单位距离的变化量,记为gradH.磁场梯度的大小为该距离上磁场强度变化率的最大值,方向为其变化率最大的方向.在不均匀磁场中,单颗磁性微粒所受磁场力的表达式为[20]
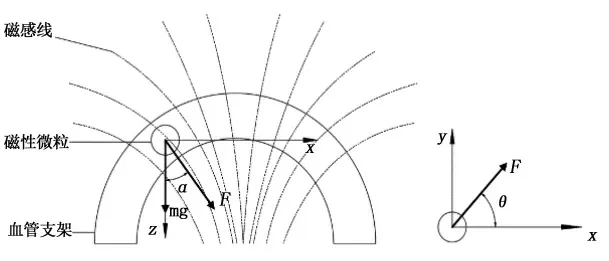
图6 单颗磁性微粒在血管支架中的受力分析Fig.6 Stress analysis of single magnetic particle in vascular stent

式(10)中:V为磁性微粒的体积,m3;χ为磁性微粒的比磁化率,m3·kg-1;H为外磁场的强度,A·m-1;gradH为磁场梯度,A·m-2.
由于磁性微粒非常小,所以可将单颗磁性微粒近似看成球体,则单颗磁性微粒所受磁场力

F为式(11)中:d为磁粒直径,m.
在磁场中磁性微粒受到的磁力F的方向和磁场梯度的方向保持一致,在非均匀磁场中磁场梯度的方向为磁场强度低的点指向磁场强度高的点.磁性微粒在非均匀磁场中的受力分析是比较复杂的,为了简化分析,把磁性微粒受到的磁力F分解成x、y、z三个方向上的标量.在z轴方向上,磁场强度和磁场梯度随着z轴递减.随着磁性微粒的位置越靠近血管支架中间,磁力F与z轴的夹角α越小;磁力F在z轴上的分量Fz随着夹角α的减小而增大,在x轴上的分量Fx随着夹角α的减小而减小.由于磁性微粒被固定在血管支架上,主要也是研究血管支架在磁力作用下载z方向上的形变,所以假设磁性微粒只在x、z平面内沿z轴运动则分量Fy=0,分量Fx很小可忽略不计,则磁力F=Fz,为了简化计算,用磁力在z轴上的分量Fz代替F,则有
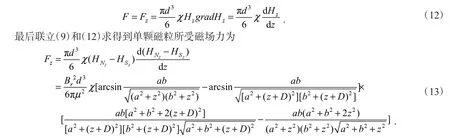
单颗磁粒所占面积过于太小,单颗磁粒产生的磁场力也不足以使血管支架产生可测量的位移,因此本文把单位区域内(1mm2)的磁粒所受磁场力的合力做一个线性叠加,有n颗磁粒就在单颗磁粒所受磁场力前面乘以系数n,把这个合力看作是使血管支架某一区域产生形变的一个点力.最后得到的公式为
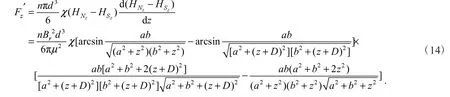
根据式(14)可知,永磁体对在z轴线上任意一点P处的磁性血管支架施加的磁场力Fz’与磁粒数量n,剩余磁感应强度Br,磁粒直径d,磁粒的比磁化率χ,永磁体的形状以及该点到永磁体表面的距离z有关.
1.3.3 磁-结构耦合理论分析 天然血管一般都具有一定弹性,人工血管支架也不例外,在不超出应力极限的外力的作用下会使血管支架产生弹性形变,确定血管支架的变形规律(即变形量与施加在血管上的力的关系)对本文后续的仿真分析与实验有着重要的作用.血管支架的变形量与血管支架的材料、形状、受力面积、力的大小以及载荷的分布有着密切的关系.血管支架应力变形的分类可根据不同的依据分为不同的分类,在此,我们根据血管支架受到的载荷形式,可以分为集中载荷引起的变形和均布载荷引起的变形两种.由于血管支架应力变形理论在微观上是比较复杂,分析推导过程也比较繁杂,因此本文只给出满足所需要的理论计算的理论公式,方便后文使用.
在本文使用的血管支架形状为圆柱环形如图7所示.在图中,lm是血管支架长度,d1是血管支架外径,d2是血管支架内径hm=d1-d2是血管支架厚度.
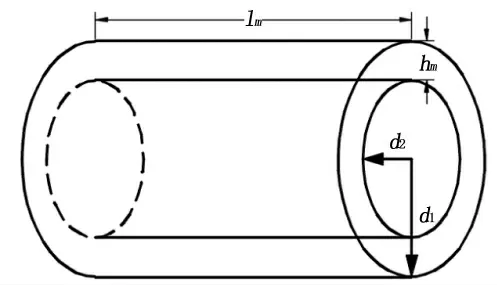
图7 磁性小口径血管支架示意Fig.7 Schematic diagram of magnetic small caliber vascular stent
在点力的作用下,力与血管支架位移偏转度的之间的关系可简单表示为[21]

式(15)中:c为取决于外缘边界条件和形状的常数(在这种情况下,对于固定边缘的长方形,c取0.005 6),dz为血管支架位移,D为材料的抗弯刚度.D定义为

式(16)中:E为杨氏模量,ν为泊松比.把公式(15)、(16)整理之后可得

联立式(14)与式(17)即可得到磁性小口径血管支架磁-结构耦合之间的理论关系
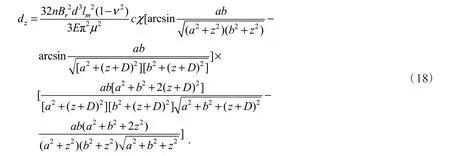
根据式(18)可知,磁性血管支架在圆柱形永磁体磁场下所产生的位移dz与磁粒数量n,剩余磁感应强度Br,磁粒直径d,磁粒的比磁化率χ,血管支架长度lm,血管材料的泊松比ν和杨氏模量E,永磁体的形状以及该点到永磁体表面的距离z有关.
2 磁-结构耦合有限元仿真分析
为了定量分析永磁体的磁场分布和磁性小口径血管支架在磁场下的最大位移,本文采用了有限元的方法来对其进行分析,使用了COMSOL Multiphysics有限元分析软件,输入变量为永磁体与血管支架的间距d和血管支架磁性微粒的不同质量分数,输入数据为磁性小口径血管支架在磁场作用下产生的位移.首先利用软件的AC/DC模块对永磁体的磁场分布进行了单独分析,然后再通过控制变量的方法,利用AC/DC模块和固体力学模块对磁性小口径血管支架进行了磁-结构耦合仿真分析.
2.1 永磁体磁场仿真
圆柱形永磁体在均匀磁场饱和充磁之后,其本身产生的磁场是不均匀的,为了更好地了解其磁场分布和尽量减小其他因素(如磁场强弱)带来的误差,因此对径向充磁的永磁体进行仿真分析:建立如图8所示模型,里面的圆柱体表示圆柱体永磁体,半径为12.5 mm,长为40 mm,充磁方向为径向充磁;外面的长方体表示空气域.设置永磁体材料为N35,仿真得到永磁体的磁通密度模分布如图9-12所示.
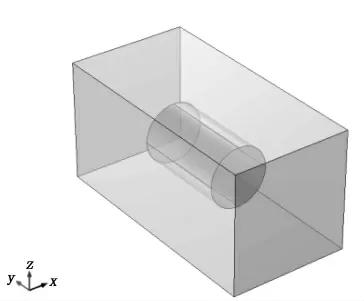
图8 圆柱形永磁体模型Fig.8 Model of cylindrical permanent magnet

图9 圆柱形永磁体y-z平面磁通密度模截面Fig.9 Cross section of Y-Z plane flux density mode of cylindrical permanent magnet

图10 圆柱形永磁体x-z平面磁通密度模截面Fig.10 Cross section of x-z plane flux density mode of cylindrical permanent magnet
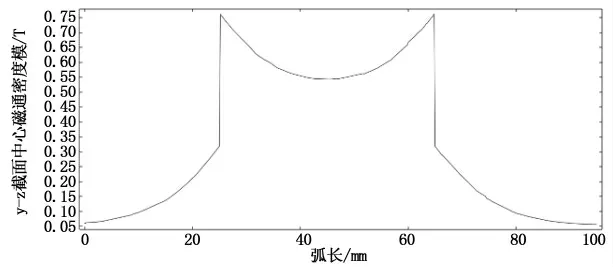
图12 y-z截面中心磁通密度Fig.12 Central magnetic flux density of Y-Z section
从仿真结果图9-12可以看出,圆柱形永磁体周围的磁感应强度在永磁体内部和距离永磁体表面较近位置均匀分布,大约为0.60 T;随着离永磁体距离的增大,磁感应强度呈非线性衰减,从表面最大值约0.75 T直线下降到约0.30 T.圆柱形永磁体磁通密度较大的地方是其内部和距离外表面较近的位置,从图8和图11还可以看出在长方形截面的四个角处,磁感应强度比其他地方的磁感应强度大,其值约为0.75 T,大于其内部的0.60 T,这是因为磁力线在磁体边缘位置相对磁体中部而言要更集中.
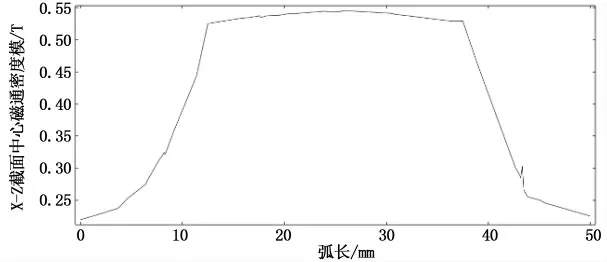
图11 x-z截面中心磁通密度Fig.11 Central magnetic flux density of x-z section
2.2 磁—结构耦合仿真
建立如图13所示模型,圆柱形永磁体半径为12.5 mm,长为40 mm;血管支架半径为1 mm,厚度为0.3 mm;圆柱形永磁体上表面与血管支架下表面之间的距离为d,空气域为60 mm×60 mm×100 mm的长方体.
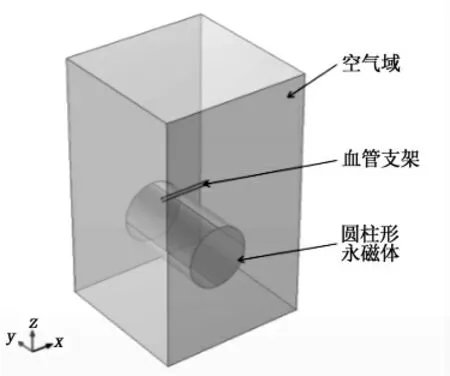
图13 磁性血管支架与永磁体模型Fig.13 Magnetic vascular stent and permanent magnet model
设置永磁体材料为N35,剩余磁通密度模为1.1 T,血管支架杨氏模量为16.4 MPa,密度为1 021 kg/m3,泊松比为0.35,磁性血管支架两端固定,永磁体与磁性小口径血管支架的距离可调节.为研究不同磁粉含量的磁性小口径血管支架在距离永磁体不同距离下的位移,将磁性血管支架按照不同质量分数分为5个组,分别为2.5%、4%、5.5%、7%和8.5%.不同质量分数的磁性小口径血管支架分别用磁化强度来表示,分别为1.1×10e4A/m、3.4×10e4A/m、5.7×10e4A/m、8×10e4A/m和1.03×10e5A/m.以2.5%质量分数的磁性小口径血管支架为例,2.5%质量分数的磁性小口径血管支架仿真结果如图14所示.
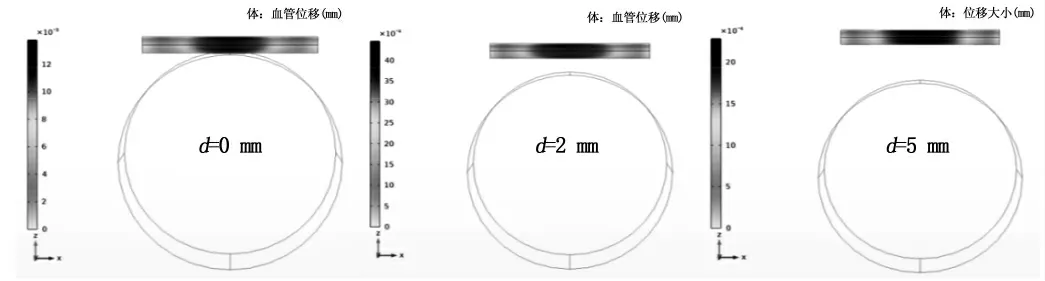
图14 2.5%质量分数的血管支架在不同距离的位移Fig.14 Displacement of vascular stent with 2.5%mass fraction at different distances
由仿真结果可知,磁性血管支架的位移随着离永磁体的距离d的增大而减小,位移从距离0 mm时的0.013 0 mm减小到距离5 mm时的0.002 2 mm;随着质量分数的增大而增大,距离为0 mm时位移从质量分数为2.5%的0.001 3 mm增加到质量分数为8.5%的0.320 0 mm.为进行数值化的研究,把磁性血管支架的最大位移作为研究对象,质量分数为2.5%、4.0%、5.5%、7.0%和8.5%的磁性小口径血管支架数据结果如表1所示.
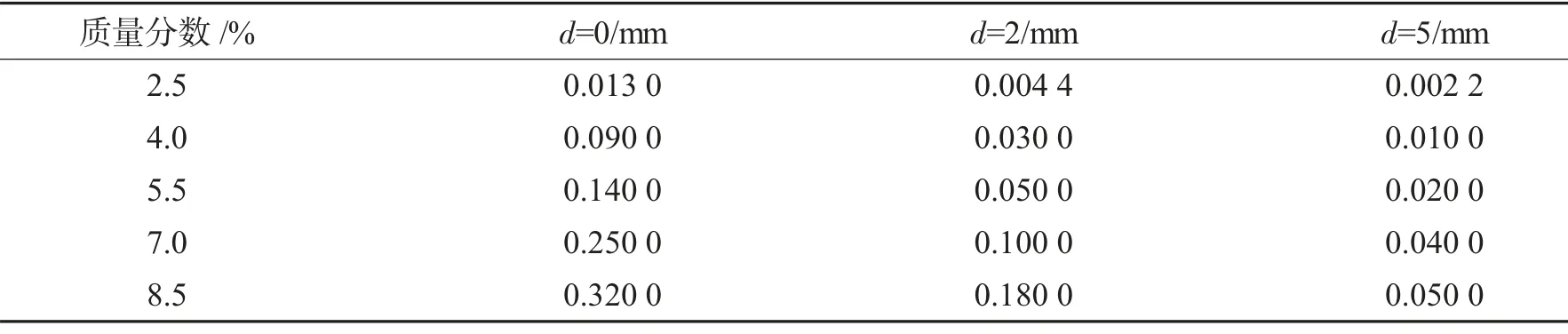
表1 不同质量分数的磁性血管支架在不同距离下的最大位移Tab.1 Maximum displacement of magnetic vascular stents with different mass fractions at different distances
3 静电纺丝磁性血管支架集成制备
血管是生物体运送血液的通道,根据血管构造的不同一般把天然血管分为动脉血管、静脉血管和毛细血管.动脉血管在心脏的搏动下可产生一定程度的脉动,人体动脉血管直径一般在15 mm左右,小鼠股动脉血管直径在2 mm左右,兔子动脉血管直径4~6 mm.考虑到生物实验需要的小鼠比较容易获取,本文制备的磁性小口径血管支架尺寸选择为2 mm.近年来利用静电纺丝、粒子沥虑和相分离等多种技术的,以PGA、PLA、PCL以及丝素蛋白等合成材料和天然材料为基质制备人工血管的技术广泛用于人工血管支架的制备,相比之下,静电纺丝技术制备人工血管简便高效,PCL具有较好的生物相容性,所以本文基于静电纺丝的方法,在PCL溶液中添加了NdFeB磁性微粒来制备小口径血管支架,磁性小口径血管支架静电纺丝原理图如图15所示.静电纺丝流程主要有静电纺丝溶液的配置、系统的搭建以及产品的制备等三个步骤,其中静电纺丝溶液的配置和产品的制备是关键步骤,磁性小口径血管支架集成制备流程如图16所示.
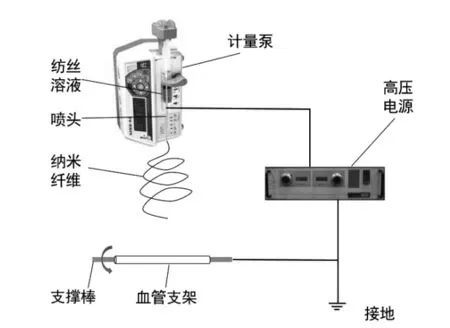
图15 静电纺丝原理Fig.15 Schematic diagram of electrospinning
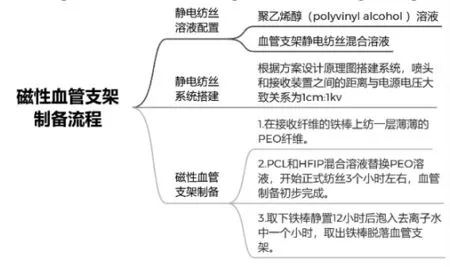
图16 磁性小口径血管支架集成制造流程Fig.16 Integrated manufacturing process of magnetic small caliber vascular stent
3.1 聚乙烯醇(polyvinyl a lcohol)溶液的配置
把聚乙烯醇与去离子水按照3.5%的比例配置好并放入玻璃瓶中,然后加入磁性转子并放置在磁力搅拌机上搅拌12 h,使其充分混合.
3.2 静电纺丝混合溶液的配置
先准备好干净的玻璃瓶,称取0.4 g的PCL放入其中,再按照8%的比例取5 mL的六氟异丙醇(Hexafluoroisopropanol)放入玻璃瓶中,玻璃瓶中放入磁力转子并置于磁力搅拌机上面搅拌24 h,搅拌完成之后再把磁性微粒按照一定比例(2.5%,4.0%,5.5%,7.0%,8.5%)称质量放入玻璃瓶中并用玻璃棒搅拌均匀即可,等纺丝系统搭建完成之后就可以转入系统储液器中.
3.3 静电纺丝制造系统搭建
把静电纺丝制造系统需要高压电源、接收装置、带金属喷头的储液器以及计量泵按照图15所示依次搭建,喷头和接收装置之间的距离与电源电压大致关系为1 cm∶1 kV.
3.4 磁性小口径血管支架的制备
(1)静电纺丝PEO溶液.为了使磁性血管支架制备完成后方便从支撑铁棒取出,先在接收纤维的铁棒上纺上一层薄薄的PEO纤维,因为PEO可以被水溶解,从而在制备完成的血管支架与支撑铁棒之间形成细小的孔隙方便血管支架的脱落.
(2)磁性血管支架的制备.把PCL和钕铁硼磁性颗粒混合溶液转入储液器,设置好计量泵的速度,再把溶液刚好推送到喷头末端,开启计量泵,使其按设定速度推送溶液,同时开启高压电源,观察并适当调整电源电压及接收装置的位置,使喷出的纤维能够被接收装置接收到.保持相对稳定的状态纺丝3 h左右,磁性血管支架初步制作完成.
(3)磁性血管支架的脱落与干燥.磁性血管支架在通风橱静置12 h挥发溶剂,之后通过浸泡脱落法把磁性血管支架脱落,然后放入冷冻干燥机干燥2 h后取出,磁性血管支架制备完成,制备完成的磁性血管支架如图17所示.

图17 制备完成的磁性血管支架Fig.17 Prepared magnetic vascular stent
4 实验测试与分析
4.1 系统搭建
为了测试所制备的磁性小口径血管支架的位移,本文按照图18实验测试系统示意图搭建了如图19所示的实验测试系统.系统装置主要由激光位移检测器、血管支架、血管支架支撑装置、磁棒以及可垂直移动的支架组成.
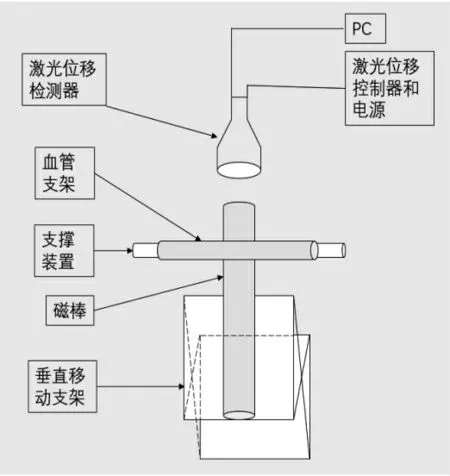
图18 实验测试示意Fig.18 Schematic diagram of experimental test

图19 实验测试系统Fig.19 Experimental test system
4.2 结果与分析
本文实验采取血管支架固定,磁棒移动的方式来测量磁性血管支架的位移.通过条件垂直移动支架来改变圆柱形永磁体上表面与磁性血管支架下表面的距离.为了减小实验的测量误差,采用多次测量最后取平均值得到最后的测试数据.为了减小实验的初始误差,先通过移动支架把磁棒移动到血管支架附近,使其上表面距离血管支架下表面0.1 mm左右,然后再把磁棒下降到距离血管支架5 cm处.调节好激光位移检测器位置后,在计算机上使其检测数值归零再进行实验.为进行数值化的研究,把每次测量的波峰波谷的最大值作为研究对象,测试实验数据如图20-24所示.
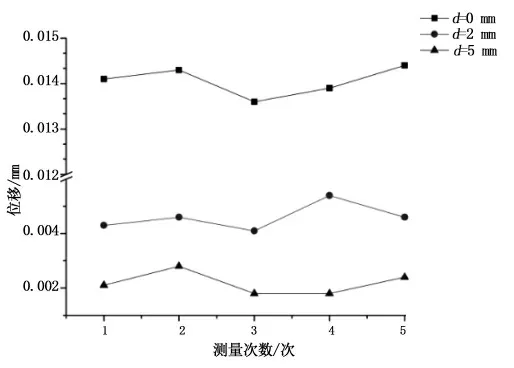
图20 2.5%质量分数磁性小口径血管支架位移测试数据Fig.20 Displacement test data of 2.5%mass fraction magnetic small caliber vascular stent
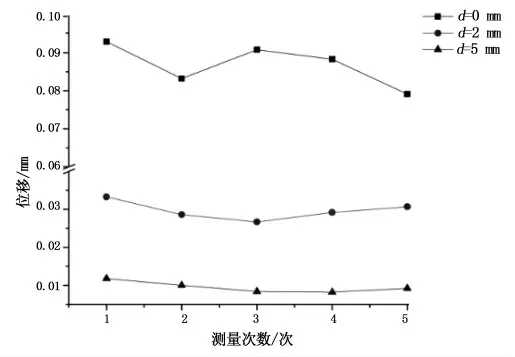
图21 4.0%质量分数磁性小口径血管支架位移测试数据Fig.21 Displacement test data of 4.0%mass fraction magnetic small caliber vascular stent
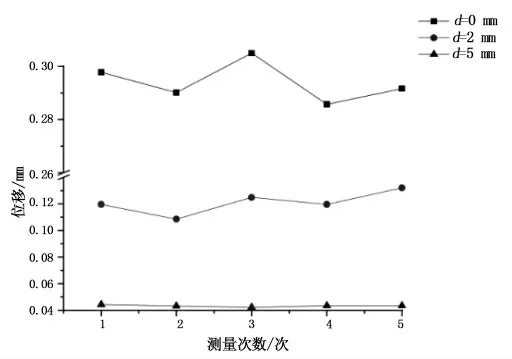
图22 5.5%质量分数磁性小口径血管支架位移测试数据Fig.22 Displacement test data of 5.5%mass fraction magnetic small caliber vascular stent
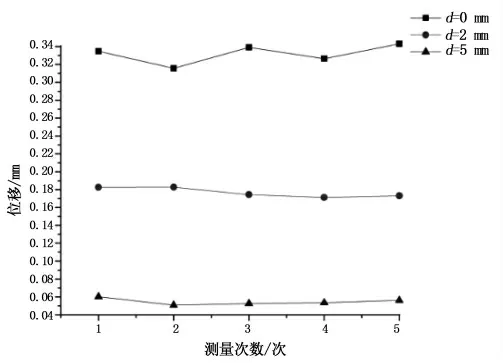
图23 7.0%质量分数磁性小口径血管支架位移测试数据Fig.23 Displacement test data of 7.0%mass fraction magnetic small caliber vascular stent
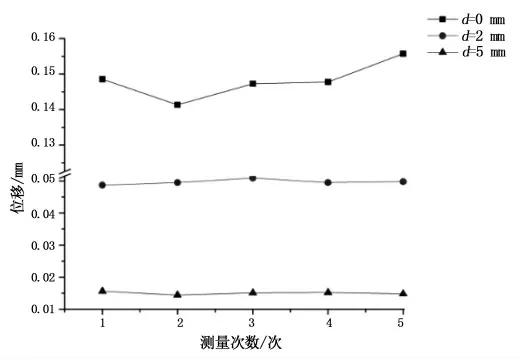
图24 8.5%质量分数磁性小口径血管支架位移测试数据Fig.24 Displacement test data of 8.5%mass fraction magnetic small caliber vascular stent
把不同质量分数、不同距离d得到的数据求平均值,得到表2的数据.把实验测试数据和仿真数据进行对比,如图25所示;进一步分析变化的位移与磁性血管支架管径大小之比,如图26所示.
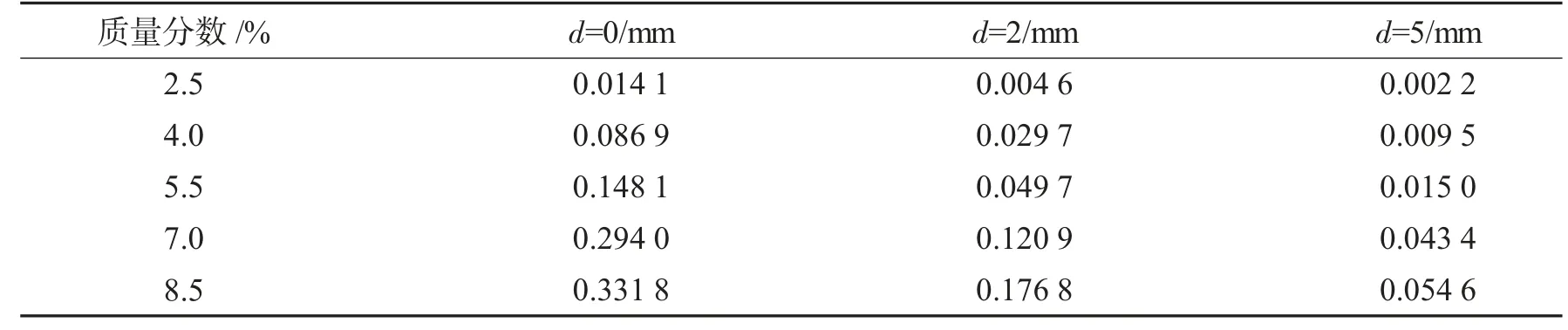
表2 不同质量分数的磁性血管支架在不同位置的平均最大位移Tab.2 Average maximum displacement of magnetic vascular stents with different mass fractions at different positions
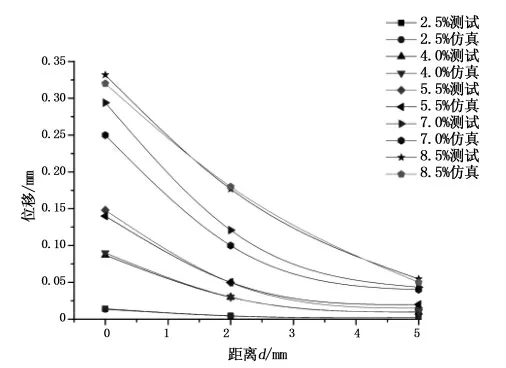
图25 不同质量分数磁性血管支架在不同距离下的测试与仿真位移对比Fig.25 Comparison of test and simulation displacement of magnetic vascular stents with different mass fractions at different distances
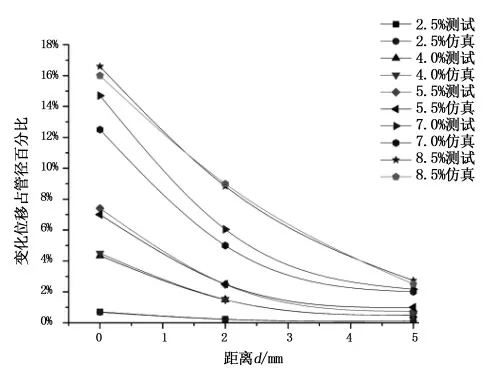
图26 不同质量分数磁性血管支架变化位移占管径大小的百分比Fig.26 Percentage of displacement of magnetic vascular stent with different mass fraction in diameter
由图25可知,在同一距离下,磁性血管支架的位移随着质量分数的增加而增加;在同一质量分数下,磁性血管支架的位移随着距离的增大而减小.除7%质量分数的磁性血管支架这一组数据相对误差在20%左右,其余各组数据相对误差都在10%以内,磁性血管支架位移的实验数据与仿真数据趋于一致.由图26可知,磁性血管支架变化位移与管径的百分比随着距离和质量分数的变化在0.1%到17%之间变化,可以把质量分数和永磁体与磁性血管支架之间的距离组合为不同的组合来满足需求的多样化.
5 小结
本文研究了一种基于静电纺丝的磁性小口径血管支架,该血管支架充磁之后可在磁力的作用下模拟天然血流脉动所产生的血管管径的变化.利用COMSOL Multiphysics软件的磁场模块对圆柱形永磁体进行了仿真,从仿真结果可以得出:圆柱形永磁体磁场强度最大的位置在其表面,逐渐向周围递减;圆柱形永磁体磁场强度的方向不定,随着空间位置的不同而改变.在同一质量分数下,磁性小口径血管支架的位移随着支架与永磁体之间距离的增加而减小,随着支架与永磁体之间距离的减小而增加.在同一距离下,磁性小口径血管支架的位移随着磁性小口径血管支架磁性微粒质量分数的增加而增加,随着磁性微粒质量分数的减小而减小,在不同情况下血管支架位移可实现0.1%到17%的变化,位移相对误差在5%左右.通过以上的仿真与测试研究,本文设计的磁性小口径血管支架可为新型生物反应容器的整体设计提供参考.

