面向流数据的多离群点检测算法研究
安云哲,吴东翰,夏秀峰,周大海,朱睿
(沈阳航空航天大学计算机学院,辽宁 沈阳 110136)
随着现代社会的发展,工业互联网、制造行业等领域产生了大量的数据,人们在关注数据整体趋势的同时,也开始越来越关注那些表现与数据集中其他数据存在明显不同的异常值,因为这些数据点往往蕴含着更加有用的信息.为了从这些数据中发掘到更有价值的信息,许多应用都依赖于数据流[1]上的离群点检测技术.而随着有关离群点检测的需求增多,用户不再满足单一的离群点检测,想要从数据中找到更多有价值的信息,从而产生许多离群点的查询任务.然而,对于这个问题,现有的离群点检测算法大多是面向单查询的检测,不能解决用户需求.因此,本文提出面向流数据的多离群点检测算法来解决这个问题.
离群点检测问题是由Knorr和Ng[2-3]先提出的.离群点检测查询旨在数据集中查找邻居个数少于k的对象.在此基础上Ramaswamy[4]修改了Knorr和Ng提出的方法,引入基于k近邻的定义,它将对象与其k近邻的距离作为对象的分数,向系统返回分值最高的n个对象.为支持该查询,该工作提出了一种基于分区的算法,来增加查询效率.但是,该工作没有考虑到一个点的k-邻域中包含的信息,因此不能正确的适用于分布密集或稀疏的邻域.所以针对这一问题,本文采取分区的方式对数据进行处理,来解决数据分布的问题,以此来提高查询效率,减少不必要的查询损失.
针对流数据上的基于距离的离群点检测算法的相关研究[4-5]中,一般采用索引的方式来对数据进行管理.基于索引的算法被Jiawei等[6]提出,该算法依赖于构建出索引(R树[7],M树[8],KD树[9]等)的性能.但是当数据的维度增加的时候,算法的性能也会降低.Bay等[10]提出了基于嵌套循环的ORCA算法,这个算法是对于基于分区的算法的改进.在该算法中,运用简单的剪枝策略和数据点随机化,可以有效的检测出符合离群点的定义.由于ORCA是基于磁盘处理的算法,而无法从内存中进行数据的读取操作,因此在大的数据集中无法使用.在文献[11]中朱利等人基于最小生成树提出了相关算法,能够自动辨认簇的数量并挖掘出不同类别的异常数据.在文献[12]中使用了KD树作为索引.虽然在使用索引结构后能够加快检测的执行时间,但是由于索引结构会随着属性数量的增加,索引的更新和维护效率下降,会影响到算法检测的效率.但是这些算法只能针对单查询问题进行解决,而且索引结构会随着属性数量的增加,索引的更新和维护效率下降,会影响到算法检测的效率.针对这一问题,本文提出一种基于网格索引的查询框架,将数据点按照维度信息进行存储.在进行查询时可以直接找到查询数据所在位置,直接返回即可.通过该方法,增加查询效率,减少维度对查询效率的影响,极大的提高了离群点检测算法的查询效率.
现有的多离群点检测算法大都通过在索引或者单查询方面进行改进.Konkaki等[13]初步探讨了在流数据的环境下多查询的离群点的检测方法.提出的算法通过减少内存的开销来增加查询效率.但是进行范围查询来搜索其邻居集合是需要花费昂贵的代价,而当滑动窗口内的数据增加的情况下,这个算法中单离群点检测的查询处理的效率也会随之下降.而Georgiadis等[14]在此基础上提出了一个可拓展的框架,虽然在运行时间和算法的灵活性上面有着较好的改进,但是对于多离群点检测的多查询处理方面还没有一个较好的方式.Gao等[15]提出的SOP方法.该算法考虑到用户不同的检测需求而衍生出多种的查询条件.该算法将多离群点检测问题转换成skyline问题,通过从滑动窗口从后向前来为每一个查询点来构建一个skyline表来进行查询.再通过每个点邻居到其的距离和到达时间的前后来回答每一个查询检测.判读查询点是否是离群点.这种方法避免了上述文献中的常规范围搜索.但是由于需要维护每个查询点的skyband点邻居表,在滑动窗口数据流入流出时对邻居表进行维护和更新,所需开销较大.针对多离群点检测方面,本文考虑到多查询任务增多的情况.因此通过多查询检测任务之间的包含关系,利用多查询之间的共享机制来支持多查询的检测问题,来降低查询规模对算法性能的影响.在查询点过程中采用索引的方式来提高查询效率,来解决多离群点检测问题.
1 多离群点检测相关定义
一般情况下,基于距离的离群点检测可以分为基于阈值、基于kmax和基于ksum的检测.本文主要关注基于阈值的离群点检测.具体地,给定两个参数阈值k和查询半径r,以及两个对象o1,o2,如果它们之间的距离小于参数r,则称o1为o2的邻居.此外,如果一个对象在查询半径内r的邻居数量大于另一个参数阈值k,则将这个对象视为非离群点,否则将其视为离群点.在滑动窗口环境中,离群点检测对窗口进行监控,并在窗口滑动时报告窗口中的所有离群点.如下图所示:D(o1,o2)=l,长度小于查询半径r,那么它们就是彼此的邻居.给定对象o3和o4,其中o3有2个邻居,少于阈值k(=3),所以o3是离群点,而o4有三个邻居,邻居的数量不小于3.因此,o4是非离群点.多离群点检测示意见图1.
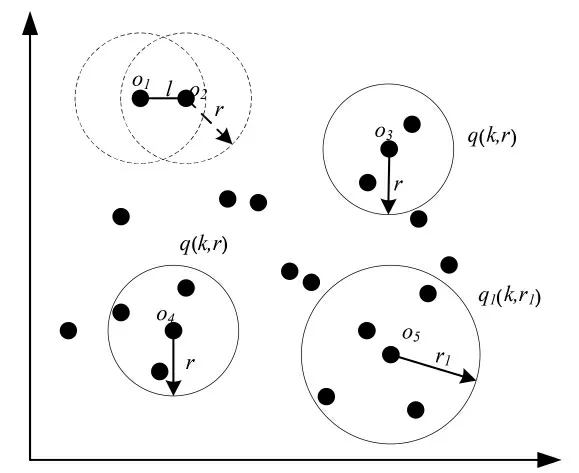
图1 多离群点检测示意Fig.1 Schematic diagram of multiple outlier detection
定义1欧式距离:给定由一组d维数据对象组成的集合D,对象oi和oj属于集合D,对象oi和对象oj的欧式距离的计算如下式
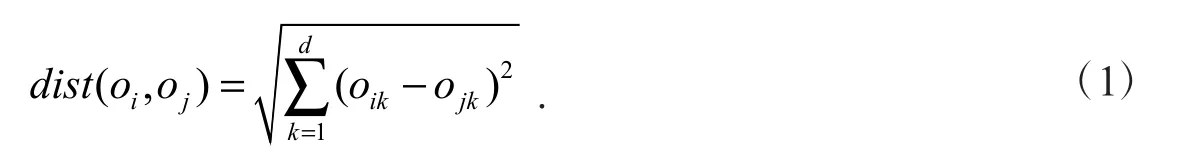
定义2邻居点:给定一组由d维数据对象组成的集合D,距离参数l,对象oi和oj属于集合D,如果对象oi和oj之间的欧式距离dist( oi, oj)≤l,则表示对象oi与对象oj互为对方的邻居.
定义3离群点:给定由一组d维数据对象组成的集合D,查询阈值k和查询半径r,对象o属于集合D,如果查询对象o在查询半径r的范围内的邻居数量少于查询阈值k,则查询对象o表示为离群点.反之则称为非离群点.
在图1中,D(o1,o2)=l,表示的是对象之间的欧氏距离为l,但是两个点之间的距离都小于给定的查询半径r,那么它们之间就是彼此的邻居.在离群点的概念中,图中o3,o4两个数据点,其中o3在查询半径的范围内的邻居的数量少于判断阈值k,根据离群点定义,o3是离群点,而o4根据定义则是非离群点.
定义4滑动窗口:给定滑动窗口W(N,S),它存在两种定义形式:分别为基于窗口容量的窗口和基于时间间隔的窗口.基于窗口容量的窗口包含N个最新到达窗口的对象,每次流入和流出窗口的对象个数为S;基于时间的窗口包含最近N个时刻到达窗口的对象,窗口每滑动一次的时间间隔为S.
定义5滑动窗口的连续离群点检测:给定一个滑动窗口W
下面通过例子来对滑动窗口上的离群点检测进行说明,如图2所示,同样给定两个参数k=3、r不变和两个对象o1,o2.S1虚线部分表示的是当前的滑动窗口,S2实线部分是滑动后的S1,滑动数量为5.当前窗口S1中,在o1的查询半径r的范围内有三个邻居分别是点

图2 滑动窗口上的离群点检测Fig.2 Outlier detection on sliding windows
定义6q(k,r)查询定义:给定一组离群点检测参数阈值k,和查询范围r.在一次离群点检测操作中返回满足查询条件为k和r的离群点的处理过程称为一次查询,用q(k,r)来表示.
定义7多查询定义:基于定义6,多离群点检测是指,返回满足一组不同的参数k与r的查询Q={q1( k1, r1),q2( k2, r2),...,qm(km,rm)}的离群点检测过程,可以定义为大Q( ki, ri).
对于基于滑动窗口的离群点检测来说,返回一次查询的结果,表示的是单查询.即给定查询阈值k和r,在滑动窗口上检测查询点r的半径范围内所包含的点数,如果包含的点数大于阈值k的话,则表示是非群群点,而这样的过程就是一个查询.那么对于多查询来说,就是多组这样阈值一次扫描来进行离群点检测的集合.如图1所示,给定两个参数k=3、r不变,表示是其中的一个查询q(k,r),另两个参数k=3、r1不变表示的是另一个查询q1(k,r1).这两个查询的查询结果一次扫描而得到.
2 多离群点检测算法
为了更好地进行离群点的检测,本文提出了一种查询处理框架MQOD(Multiple Query of Outlier Detection)支持多离群点检测.首先利用多查询集合中子查询任务间的包含关系减少查询次数.其次,再采用分片技术对于查询点进行搜索,减少查询次数,提高查询效率.
2.1 MQOD查询算法框架
由介绍的多查询的定义可知,多离群点检测就是多个单查询任务组成的离群点检测问题.对于单个查询的离群点检测问题,可以通过遍历数据集来判断是否查询点是否是离群点.但是这种方式不适合多查询任务,这种方式会造成资源的浪费.
正如前文提到的问题,在多离群点检测的问题中需要解决多查询任务的问题.在检测过程中不能对每个查询都进行一次查询,这个过于浪费时间.算法的思想是:利用多查询之间的共享机制,可以减少不必要的时间开销.在多查询任务进行离群点检测时,有些查询任务在检测时,会查找到并计算其他查询任务所需要的邻居集合的部分数据点,而如果直接再重新对剩下的查询任务进行检测的话,就会造成这方面的计算的浪费.
基于此,本文提出一种利用查询任务之间的共享机制,提出一种基于面向流数据的多离群点检测算法MQOD.给一组多查询集合Q={q1( k1, r1),q2( k2, r2),...,qm(km,rm)},为了减少多查询的离群点检测的次数,提高查询效率.由于每个查询在搜索的过程中都会去在查询半径的范围内找到自身所需要的邻居集合来判断查询点是不是离群点,因此如果能够通过一次查询操作,就能找到其满足他查询任务所需要的邻居集合,就不需要再进行多次查询来操作寻找各自的邻居集合.因此,利用查询任务范围阈值的关系来进行解决这个问题,即在每组构建一个最大的子查询,这个最大的子查询范围阈值内的邻居集合,通过这个集合去支持其他所有查询任务的判定.
基于上述思想,通过构建一个范围查询Range(r)来找到所需要的邻居集,其中范围阈值r的大小为分组查询中查询半径最大的那个.这样,只需要对查询点进行一次范围查询就能得到所有查询任务所需要的邻居集合,再通过这个集合去判断查询点对于查询任务是否为离群点即可.
如图3所示,在二维空间中,给定三个查询q1(k1,r1),q2(k2,r2),q3(k3,r3),分别对点o进行离群点检测.其中查询q3(k3,r3)的邻居阈值k与范围阈值r最大,所以这里所需选择的最大的查询半径是r3.因此构建查询任务Range(r3).如图所示,在查询Range(r3)范围阈值r3的范围内包含查询点o的12个邻居,其中包含三个查询任务的邻居集合.q1(k1,r1),q2(k2,r2),q3(k3,r3)可以在这12个邻居中找到其查询半径内的邻居,来判断查询点是否为离群点.
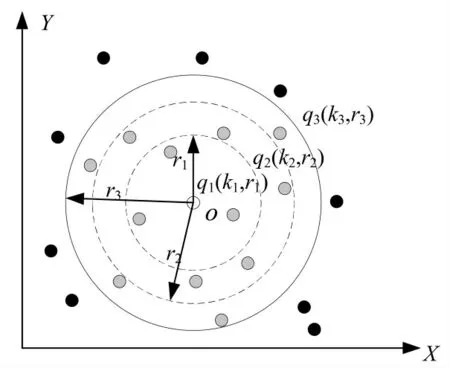
图3 范围查询的邻居集合Fig.3 Neighbor set for range query
下面介绍范围查询算法.

算法1是离群点的范围查询,返回的是第一次范围查询后的邻居点集合.算法首先计算查询范围,在查询集合Q={q1( k1, r1),q2( k2, r2),...,qm(km,rm)}中找到其中查询半径最大的当作查询范围,并构建范围查询集合(详见算法3-6行).算法的7到10行说明了范围查询的具体执行过程,第一次范围查询是从滑动窗口的后半部分,然后依次从后向前进行查找.算法先计算流入点oin的空间位置信息,再通过该点的位置信息得到其周围网格的位置,最后在这些网格中进行搜索其邻居点,并得到查询点的邻居集合.最后,按照邻居点和查询点之间的距离进行排序并返回邻居集合.
2.2 MQOD查询算法索引结构
为了更高效地进行离群点检测,本文提出HT-Grid索引结构来管理滑动窗口上的数据.该索引结构是将离群点在空间中的位置特性和网格索引相结合,再利用hash表进行快速更新与查找的一种索引结构,它能够帮助算法实现离群点的快速检测.其次,该索引结构的实现主要是利用数据点的维度信息,将这些维度空间位置的信息进行换算,得到数据点在HT-Grid索引的存储位置,然后再进行插入或删除操作.由于HT-Grid索引和hash相结合,只需要在hash表HT上O(1)的时间复杂度内进行查找就能直接确定数据所处位置,减少了搜索的时间.此外,该索引还能够通过hash表降低维度增加所引发的空间代价.
如图4所示,HT-Grid索引结构由两个部分构成,分别是管理滑动窗口W内的数据点的空间位置的虚拟网格,以及管理虚拟网格相对位置的HT索引.使用HT索引的目的是为了更加快速的找到查询点所在的位置,方便查询操作.在虚拟网格内,为了方便离群点检测时邻居集合的范围查询,在逻辑上将网格窗口按照时间顺序进行分割,对应滑动窗口划分的位置.图4中,网格中有一个查询点o,它的二维空间信息是(x,y),计算可知:查询点o位于ID为(3,3)的单元格中.算法可根据单元格id信息计算该单元格的Z-地址,进而通过哈希函数将点o映射到相应的桶内.如果该桶尚为空,算法初始化一个空桶,将该空桶插入索引,随后将对象插入该桶.否则,算法可直接将对象o插入该桶.
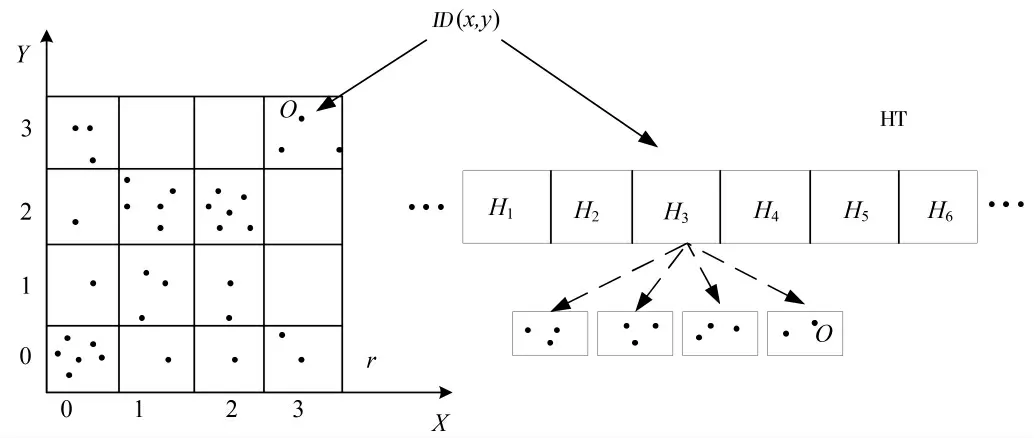
图4 HT-Grid索引构造Fig.4 HT-Grid Index Construction
为了更好地进行范围搜索,算法在逻辑上将网格内的点按照时间顺序进行分组,利用滑动窗口的开始和结束的位置,将网格分成4组.在查询的时候,优先从时间排在后面的组进行搜索,尽量搜索到查询点后面的邻居,如果能找到满足使一个查询点成为安全点的邻居数量,那么对于一些查询来说就不需要再考虑这个点了.这样一来,访问对象数目可有效降低.
正是由于滑动窗口内的点的时间特性,该算法在离群点检测的时候采取从后向前的方式对于滑动窗口内的点进行搜索.首先,算法用分片技术对滑动窗口进行分片,将窗口分成4部分,分别在窗口的1/2,1/4,1/8处进行划分.这样在进行邻居查询的时候,首先在窗口的后1/2部分开始,从后向前的顺序在网格中进行查找判断.如果窗口后1/2部分的点,能够找到支持所有查询的邻居集合的时候就停止搜索.相反的话,如果没有找到这样的邻居集合的话,就继续向前查找窗口1/4长度的数据点.再进行判断,依然不足的话,最后再去寻找窗口长度为1/8的点,直至窗口最后剩下的部分.
如图5所示,图中的数据为二维数据,其中X,Y表示数据点的邻居阈值和范围阈值两个维度的信息.图5-a表示的是滑动窗口内部的点所存储的网格结构,当查询点o进行查询时,首先通过hash计算得到其所在的网格位置并且得到其周围邻居网格的hash位置,然后在这些网格中利用流数据的时间属性来从后向前找到查询点的邻居集合,如果网格内部没有点则直接可以滤过,只需要找有点的网格即可.图5-b表示的是每次查找的范围,网格中设有标签,每次查询递进剩余窗口大小的一半,最小为窗口长度的1/8,如果刚开始就在滑动窗口的后一半就能找到所需要的邻居点集合那么就不需要再向前递进查找了,这样减少不必要的搜索次数.
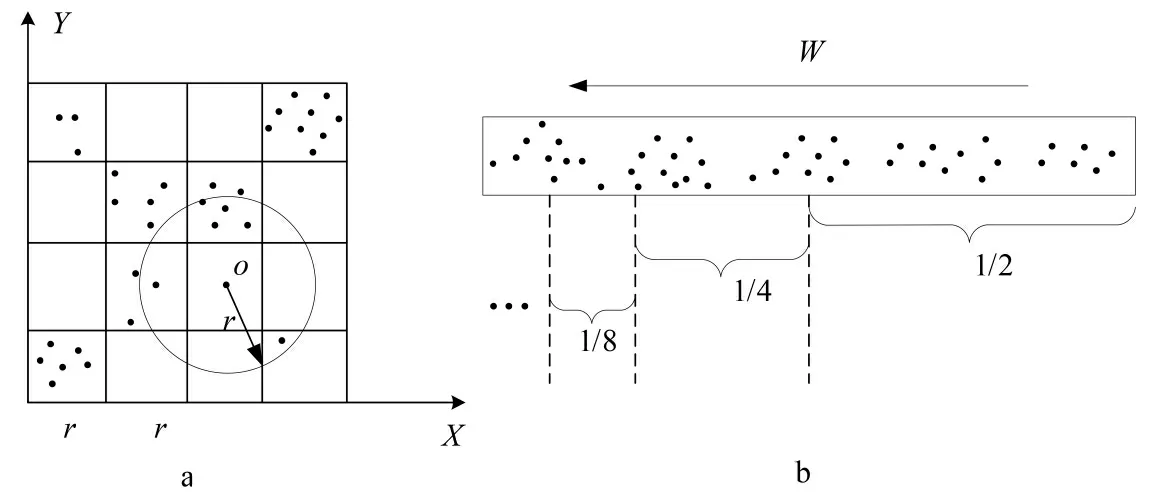
图5 HT-Grid索引范围查询Fig.5 HT-Grid Index Range Query
2.3 MQOD多查询检测算法
在得到每组最大的范围内的邻居集合之后,需要对所有的支配的集合查询进行离群点判定问题.在这里,使用k邻近距离的概念去解决这个问题.
定义8k-邻近距离(k-distance):给定一组数据集,集合中在距离数据点o最近的几个点中,第k个最近的点跟点o之间的距离,则称为点o的k-邻近距离,记为k-distance(o).
根据k临近距离的概念,来回答其他查询的判定问题.值得注意的是查询点o的k-近邻距离的点并不唯一,有可能有多个数据点和查询点o的距离与k-邻近距离相同,这些点都是查询点k-邻近距离的点.利用这一点,当 范围查询算法的返回查询点的邻居集合后,再根据分组的各个查询任务阈值k来找到查询点的k-distance(o).如果对于一个查询q(k,r)来说,查询点的o的k-distance(o)不大于查询半径r的话,也就是说在查询半径范围内至少有k个点是查询点的邻居,那么对于查询q(k,r)来说,查询点o不是离群点.相反,如果查询点o的k-distance(o)大于查询半径r的话,则表示在查询范围内的邻居集合的数量少于查询阈值k,查询点o对于查询q(k,r)来说是离群点.因为多离群点检测的查询之间的顺序是按照查询阈值k从小到大的顺序进行排列的,所以只要在范围查询的邻居集合中按照k-distance(o)与需要检测的查询半径进行比较即可.下面将介绍多查询分组检测算法.
算法2:多查询检测算法

3 实验验证
3.1 实验条件
本文算法均由C++语言编写,使用VS2019进行编译.实验平台为Win10操作系统,CPU型号为Intel(R)Xeon(R)Gold 6226R CPU@2.90GHz,2.89 GHz,内存256GB.
3.2 实验数据
(1)数据集:为了增加实验的可信度,本文采取5个数据集进行算法的验证.其中Tao、Stock两个是真实的数据集,其它为合成的数据集.其中Tao是一个热带海洋项目的数据,本文只使用了其中较小的一部分,包含了共575 648条记录数据,每条数据有3个属性.真实数据集Stock为中国深沪两市2015—2016年约2 300支股票的交易记录,原始数据规模约为30 GB.实验对数据进行清洗.首先将数据中非数值信息进行剔除,只保留数值信息;其次对数据中缺失数值的记录进行删除,再进行去重后,只保留剩下的数值记录.在对数据进行清洗之后,取确认数据集中的3个属性,来作为本文实验数据集,数据规模为1 GB左右,60余万条数据.最后的三个合成数据集SD1、SD2、SD3,最大的SD1数据集为100万条数据,SD2、SD3分别为30和70万条数据,为随机生成的数据集.
(2)参数设置:针对多离群点检测的参数设置问题,首先是查询任务的数量的不同,意即查询任务中查询阈值和查询半径的不同.其次,针对多查询索引结构来说,索引的构建时间和索引的更新效率也需要被评估.其中参数设置中的N是表示滑动窗口的长度,s表示的滑动窗口数据每次流入流出的数量,k和r分别表示的多查询任务的查询阈值和查询范围.实验参数设置见表1.

表1 实验参数设置Tab.1 Parameter Settings
(3)实验方法:本文选用流数据上的两种离群点检测算法exact-Storm算法和abstract-C作为对比试验.由于两种算法仅适用于单查询,为了更好地与本文的实验进行对比,对于两种算法按照顺序进行执行,以此来保障对比效果.本文将从查询集合任务数量、数据量大小、窗口大小三个方面在三个数据集上进行实验对比.
3.3 实验结果分析
3.3.1 查询数量对于算法的影响 实验结果如图6所示,在图中分别对两组数据量相近的数据集进行实验,其中图6-a表示的是数据集tao,图6-b表示的是数据集stock.在图6中的两个实验中,设置的默认窗口长度是10 000,默认的窗口流速为500,设置了不同的查询任务数量为{10,20,30,40,50}.可以看出,随着查询数量的增加三个算法的时间开销也相应的增多.本文算法MQOD并不会随着查询数量的增多而出现明显的增长变化,而是保持相对稳定的状态,而算法exact-Storm和算法abstract-C则会随着查询数量的增多呈现明显的上升趋势,因而在进行多离群点检测时,这两个算法判断检测的代价会随之增加,也会造成不必要的时间成本.与abstract-C算法相比,算法exact-Storm在查询效率上具有优势.
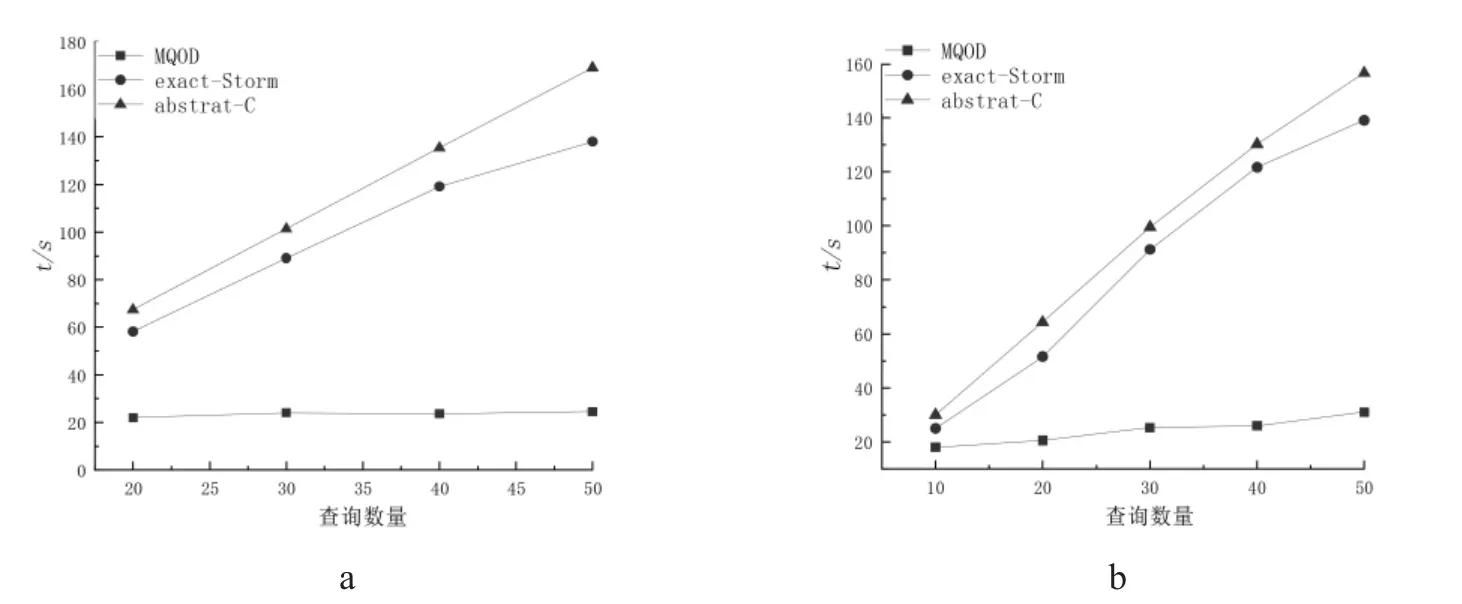
图6 查询数量对查询的影响Fig.6 Query efficiency vary Numbers
3.3.2 数据集大小对于多查询的影响 为了更加直观的对数据算法进行验证,使用合成数据30万个点和70万个点的两个集合进行实验.在实验中,设置查询任务的数量为50,其中的查询阈值和查询半径互不相同,滑动窗口的流速与上文相同.实验结果如图7所示.图7主要是通过数据集中点数的变化来判断多查询算法的效率,查询集合选择{30,50,70,100}四个数据集,单位是103.从图7中可以看出算法exact-Storm和abstract-C的多离群点的检测时间会随着查询的数据集的大小成线性增加,在数据集大的时候相应的检测时间也会增多.本文提出的离群点检测算法,在处理多查询任务时会根据任务的阈值和查询半径来进行分组来减少查询次数,保障用尽可能少的查询遍历次数来回答所用的查询任务,因此相对于其他两个对比算法来说,不会出现时间随着数据集的增大而出现明显增长情况,多查询的检测时间的表现比较稳定.
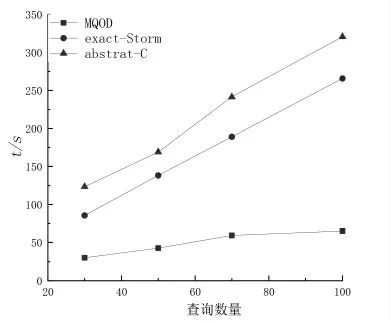
图7 数据集大小对查询影响Fig.7 Query efficiency of Dataset size
3.3.3 窗口大小对多查询算法的影响 本文采用stock作为实验的数据集合,实验结果如图8所示.从图中可以看出,查询窗口较小的时候,三个算法的效率基本相同.随着窗口的增大,需要处理的数据也相应的增多,花费的时间也明显的增多.算法exact-Storm和算法abstract-C在10 kb窗口大小之前效果基本一致,在窗口增加到一半时,出现明显变大的趋势,而本文算法MQOD的表现较为稳定.
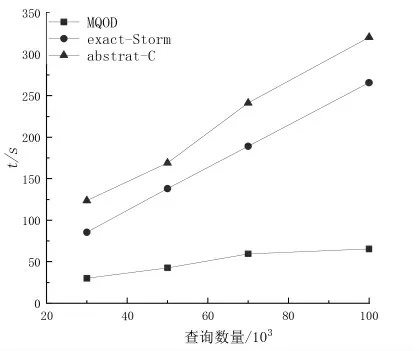
图8 窗口大小对查询的影响Fig.8 Query efficiency vary Windowsize
4 小结
离群点检测问题作为数据挖掘领域中的一个重要研究,本文提出面向流数据的多离群点检测算法,该算法能够对数据流中的离群点进行快速检测和更新,利用查询条件之间的包含关系来减少查询次数.进一步提出HT-Grid索引结构,对数据流进行管理,减少搜索代价,增加查询效率.并通过实验验证了该算法的有效性和稳定性.下一步工作中,我们将考虑进一步的提高分组查询方法,从而提高查询效率.

