35 MPa 玄武岩纤维增强复合材料气瓶快速充装温升数值模拟

韩 锐，李 明，郭永智,，卿 平，孙宇恒，何太碧,6*

（1.西华大学材料科学与工程学院,四川 成都 610039；2.电子科技大学光电科学与工程学院,四川 成都 611731；3.中材科技(成都)有限公司,四川 成都 611435；4.西华大学汽车与交通学院,四川 成都 610039；5.三一汽车起重机械有限公司,湖南 长沙 410699；6.西华大学流体及动力机械教育部重点实验室,四川 成都 610039）

压缩天然气（CNG）作为车用燃料通常被储存在耐压气瓶中。当前，国内车用CNG 气瓶充装压力多为20 MPa，能量密度低、续航里程短。为了增加燃气汽车的续航里程同时兼顾行驶经济性，与国际接轨，对质量轻、储存密度高的35 MPa 高压复合材料CNG 气瓶的优化设计与制备已被日益重视。

复合材料气瓶的结构主要由内衬和纤维缠绕层两部分组成。在复合材料气瓶服役过程中，温度是影响其性能的重要因素之一，过高的温度会造成纤维缠绕层剥离，弱化气瓶耐高压性能，因此ISO11439– 2013《车用压缩天然气高压气瓶》[1]要求，气瓶的使用温度不得超过82 ℃。而CNG 气瓶的天然气加注过程要求在5～10 min 内完成[2]，易使气瓶内部温度剧烈升高，超过限定值，造成复合材料气瓶纤维层剥离失效，影响其使用安全。另一方面，充装时气瓶内温升效应过高，会导致天然气充装质量低于额定值，此时一般通过提高充装压力来补偿，容易引发危险[3]。因此，对CNG 气瓶进行快充温升效应的研究很有必要。

国内外已开展气瓶充装模拟研究多年。Hirotani等[3]研究了35 MPa 工作压力下，不同容积、不同类型气瓶在不同充装速率下的温升效应，并提出了一种阶梯式的升压模式。Farzaneh-Gord 等[4]基于热力学定律和质量平衡原理，研究了天然气成分对气瓶快速充装过程中的影响，综合考虑甲烷含量、温度变化和压缩机做功等因素，得出甲烷含量低的天然气更有利于快速充装。刘格思[5]研究了不同升压模式和充装速率对气瓶内部温升变化的影响，总结出了在快速充装过程中气瓶内部温升效应的变化规律。高东[6]通过数值模拟计算了非金属内胆30 MPa 玻璃纤维全缠绕复合材料气瓶，内部气体及壁面的温度分布情况，确认了该工况下气瓶充装的安全性。但目前，性能优异、生命周期清洁环保、价格低廉的玄武岩纤维还未实际应用于复合材料高压气瓶，对于35 MPa 工作压力下玄武岩纤维缠绕复合材料气瓶快速充装的温升效应还鲜有研究，特别是玄武岩纤维特殊的本征力学性能带来的气瓶设计差异，及其低热传导率带来的充装传热差异，能否满足纤维缠绕复合材料气瓶快充温升的相关要求仍存疑。本文针对前期建立的35 MPa 玄武岩纤维缠绕复合材料气瓶模型[7]进行CNG 快速充装模拟，分析5 min 内将气瓶内部压力升高到35 MPa 过程中，气瓶内部温度及压力变化规律，同时讨论温升效应的影响因素，为车用35 MPa 玄武岩纤维缠绕复合材料气瓶的应用提供依据。

1 充装过程简化模型

在天然气汽车的实际充装过程中，影响因素较多，包括加气时的环境温度、从储气井到气瓶之间的管路连接情况、阀门、加气枪等。为便于模型搭建，本文将气瓶的充装过程进行简化。简化模型见图1，主要包括高压储气罐、节流阀和CNG 气瓶。模型简化后，造成天然气在充装过程中温度升高的因素有3 个方面：1）天然气从气瓶接嘴进入气瓶内部发生节流效应，也就是Joule-Thomson 效应[8−9]；2）天然气以一定速度充入气瓶后动能转化成内能；3）充入气瓶后的天然气不断被压缩，体积功向内能转化。与此同时，存在部分热量通过壁面传热，经由铝合金内衬和玄武岩纤维缠绕层扩散到环境中[10]。

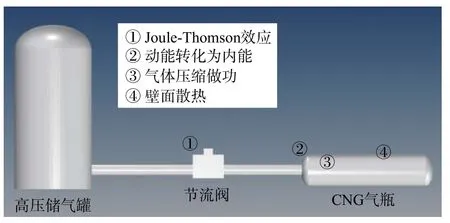
图1 快充过程简化模型Fig.1 Simplified model of fast charging process

2 CFD 数值模拟

在保证模拟精度的前提下，本文建立了2 维轴对称CFD 有限元模型。模型运用Workbench ICEM 模块划分网格并进行网格独立性研究，发现当该模型网格数达到32367、节点数为15641 后，对网格进一步细化模拟结果不再发生明显的变化，即当前网格数量为32367 时能满足计算精度要求。根据Bourgeois 等[10]的结论，本文模拟过程忽略充气过程中的浮力效应，主要考虑节流效应、压缩做功以及气体动能转化成内能对气瓶温升的影响。如图2 所示，紫色部分为气瓶内部流场，绿色部分为铝合金内衬，红色部分为玄武岩纤维缠绕层。

图2 气瓶网格模型Fig.2 Gas cylinder grid model

2.1 数值模拟控制方程

1）连续性方程。

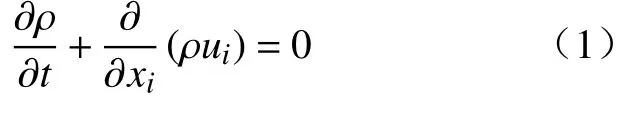
2）动量方程。

在惯性（非加速）坐标系中i方向上的动量守恒方程为

式中：p为静压，Pa；Tij为偏应力张量。

3）湍流方程。

4）能量方程。

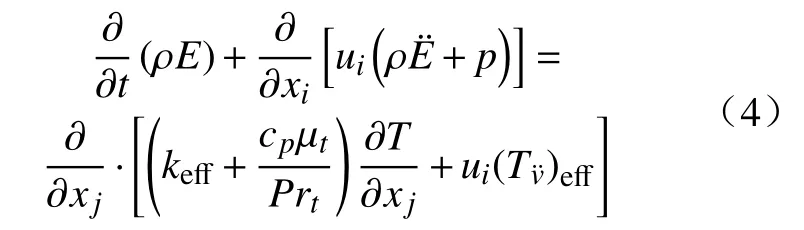
式中：k为导热系数，W·(m·K)−1；(Tv)eff为有效偏应力张量；E为总能，J。

5）气体状态方程。

有限元模型中气体状态采用真实气体状态方程Modified Benedict-Webb-Rubin 进行控制，方程如下：

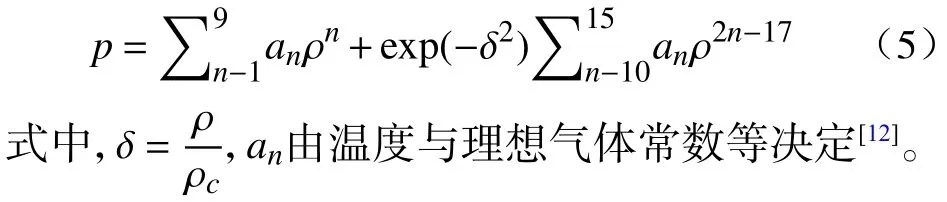
2.2 有限元模型参数与边界条件设定

2.2.1 材料参数设定

根据气瓶模型以及模拟条件，本文将复合材料气瓶分为3 个区域，分别是气瓶内部流场、铝合金内衬和玄武岩纤维/热固性树脂复合材料层。天然气属于理想可压缩气体，铝合金内衬和玄武岩纤维材料的物理性质见表1[13−14]。

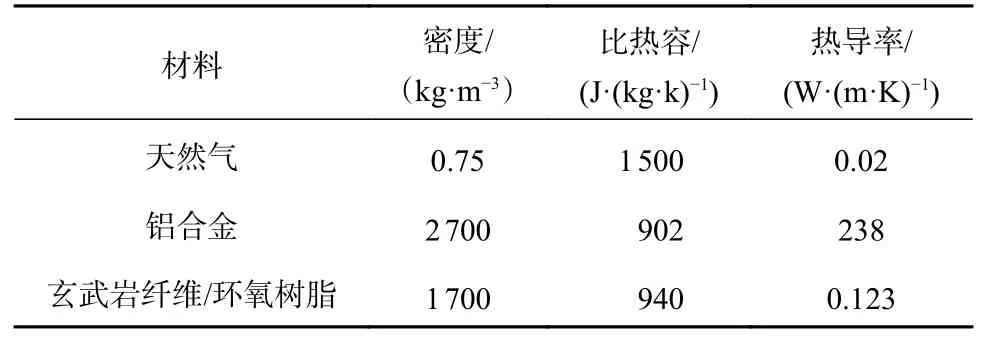
表1 气瓶材料的物理性质Tab.1 Physical properties of cylinder materials

2.2.2 边界和初始条件

天然气汽车加注过程一般要求在3～5 min 之内完成。本文设定为5 min 充装完毕，使用线性升压的进口边界来描述。充装的背压设定为45 MPa，瓶内初始压力设置为2 MPa，充装结束时压力升至工作压力，环境温度和气瓶的内部温度均设置为293 K。充装过程属于非稳态的过程，为了保证计算结果收敛，应添加时间步长和每步迭代次数进行控制。时间步长取0.5 s，最大迭代次数为20 次，设置步长为600 步。为加速收敛，计算采用的Fluent求解器为耦合隐式算法（Coupled Implicit)，瞬时方程采用一阶隐式算法。此外，气瓶外壁的传热形式为自然对流换热，本文取对流换热系数为10 W/m2·K[15−16]。

2.3 CFD 计算结果分析

2.3.1 温度分布云图

根据上述边界和初始条件，模拟得到了充装过程中气瓶的温度分布状况，如图3 所示。

图3 充装过程不同时刻的温度分布云图Fig.3 Temperature distribution cloud diagram at different times in the charging process

2.3.2 有限元结果分析

由图3 可知，充装开始后，气瓶内温度缓慢升高，最高温度出现在充装300 s，即充装结束时，最大值为333 K（60 ℃），温升为40 K，满足ISO 11439–2013 的要求。当充装时刻t=30 s 时，最高温度分布在气瓶尾部，最低温度在气瓶入口位置，且为充装时的初始温度。内衬壁面温度与气瓶内温度基本相同，且上壁面温度高于下壁面温度，满足气体流动基本原理。t=60 s 时，气瓶内温升高至296 K，位置在封头上部，温度梯度从气瓶入口位置向气瓶尾部逐渐递减，但瓶口处温度依然为天然气初始温度。随着充装时间的推移，气瓶内温度逐渐升高，120 s 时最高温度为300 K，180 s 时最高温度为311 K，240 s 时最高温度为327 K，充装结束时，温度达到333 K。在湍流的作用下，气瓶尾部的温度最先达到最高，逐渐过渡到气瓶入口处。气瓶内衬温度几乎和气瓶内部温度相当，玄武岩纤维缠绕层温度低于内衬和气瓶内部温度，充装结束后温度为316 K，表明玄武岩纤维缠绕层未对气瓶传热产生明显的不良影响。

2.3.3 气瓶内部压力变化

气瓶充装前初始压力为2 MPa，恒速升压至气瓶工作压力35 MPa，充装时间为300 s，充装结束时压力分布云图如图4 所示。

图4 充装结束压力分布云图Fig.4 Pressure distribution cloud at the end of charging

从图4 可以看出，充装结束时，气瓶内压力分布均匀，且从图5 中可以看出，气瓶内部压力随着充装时间的推移，呈线性升高的趋势，气瓶内的升压速率为0.11 MPa/s。

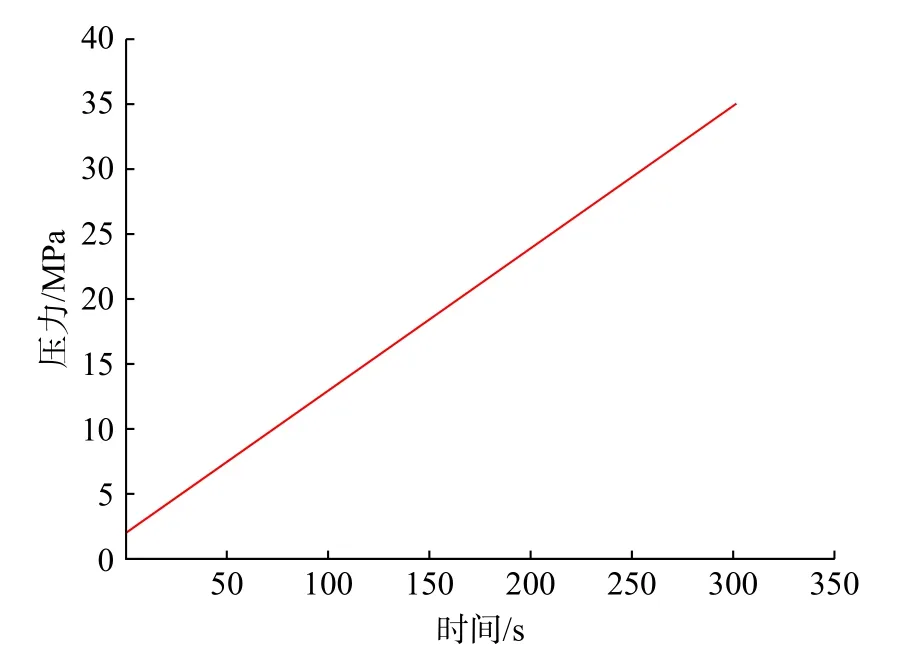
图5 气瓶内部压力－时间关系图Fig.5 Internal pressure -time diagram of gas cylinder

3 温升效应的影响因素

3.1 充装时间

当充装终止压力保持不变时，充装时间的变化实际反映了不同的充装速率。如图6 所示，保持其他充装参数不变，在充装时间为60 s 时，气瓶内最终温升幅度高达68 K，而充装时间为300 s 时，气瓶内温升幅度仅40 K。因此，当充装时间较短时，气瓶内部温升明显；随着充装时间的延长，气瓶内部的温升也随之降低，表明增加充装时间可以降低瓶内气体的温升效应，但过长的充装时间不能满足CNG 汽车实际充装要求。进一步通过Origin软件对数据进行拟合，以充装时间为自变量，温升为因变量，得到充装时间与快充温升的函数关系为：y=−0.11x+72.63，拟合度为0.969 01，说明充装时间与温升间存在负相关的线性关联。综合考虑，当充装背压为45 MPa，瓶内初始压力为2 MPa，环境温度为293 K 时，将充装时间定为100 s 至300 s区间可兼顾充装效率和温升控制。

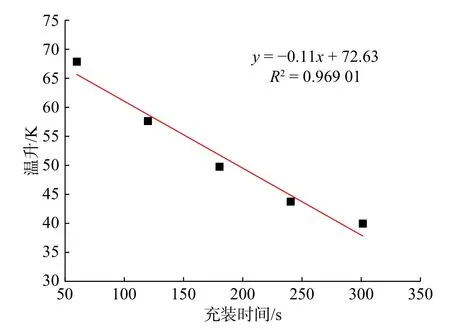
图6 充装时间对快充温升的影响规律Fig.6 Effect of charging time on fast charging temperature rise

3.2 环境温度

对于实际充装过程，天然气加注系统和CNG气瓶的充装起始温度就等于环境温度。图7 为保持充装背压45 MPa，瓶内初始压力2 MPa，充装时间为5 min 的条件不变，环境温度对快充温升的影响规律。由图可以看出，环境温度越高，温升效应越明显。对环境温度– 温升数据进行线性拟合，得出环境温度和温升的函数关系式为：y=0.85x−210.89，拟合度为0.996 57。根据函数关系式可知，起始温度每升高1 K，瓶内气体的最终温升将上升约0.85 K。经计算，在现有初始条件下，环境温度大于305 K（32 ℃），即有可能导致气瓶温度超过ISO 11439– 2013 规定的气瓶使用温度上限值82 ℃（355 K）。因此，在环境温度高于305 K（32 ℃）的炎热环境中，应适当放缓充装速率，以确保本文气瓶在充装35 MPa CNG 介质后，仍具有满足标准要求的使用寿命。

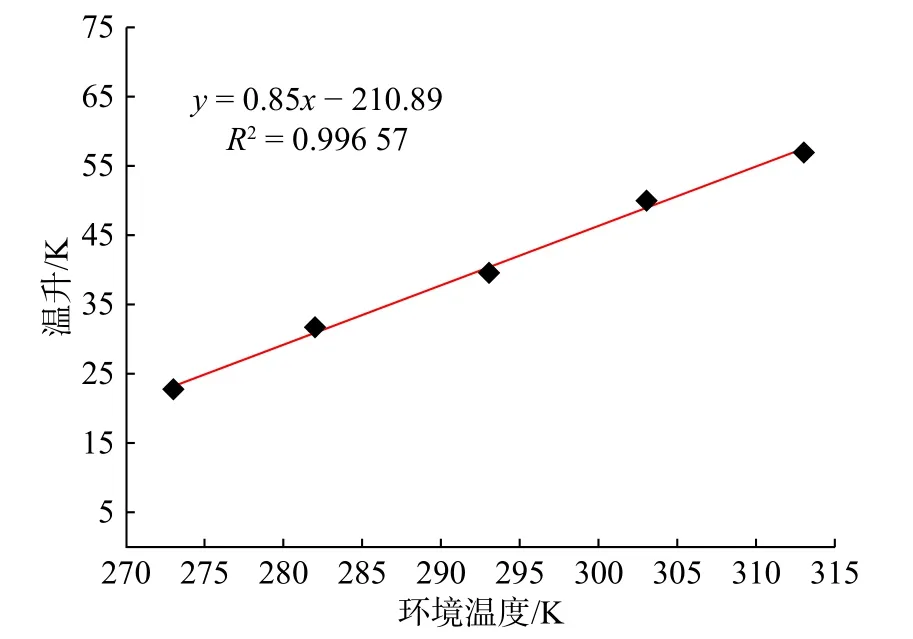
图7 环境温度对快充温升的影响规律Fig.7 Influence of ambient temperature on fast charging temperature rise

3.3 瓶内初始压力

图8 为瓶内气体温升随瓶内初始压力的变化规律。充装背压仍为45 MPa，充装时间和环境温度仍为5 min 和293 K。由图可以看出：随着气瓶瓶内初始压力的增大，气瓶内部的残留气体越多，气瓶温升效应越小；当瓶内初始压力为25 MPa 时，充装终止时气瓶内部温度仅升高11 K。对数据进行线性拟合，得出瓶内初始压力与温升的函数关系式为：y=−1.28x+41.43，拟合度为0.977 68。显然，瓶内初始压力即使为0，快充温升也能满足标准要求，且瓶内初始压力与最终温升存在反比例关系。由此可见，与延长锂电池使用寿命的“满充满放”要求不同，在35 MPa 玄武岩纤维增强复合材料气瓶的使用过程中，应适当避免“用干用尽”瓶内天然气，减弱温升效应，延长气瓶的使用寿命。

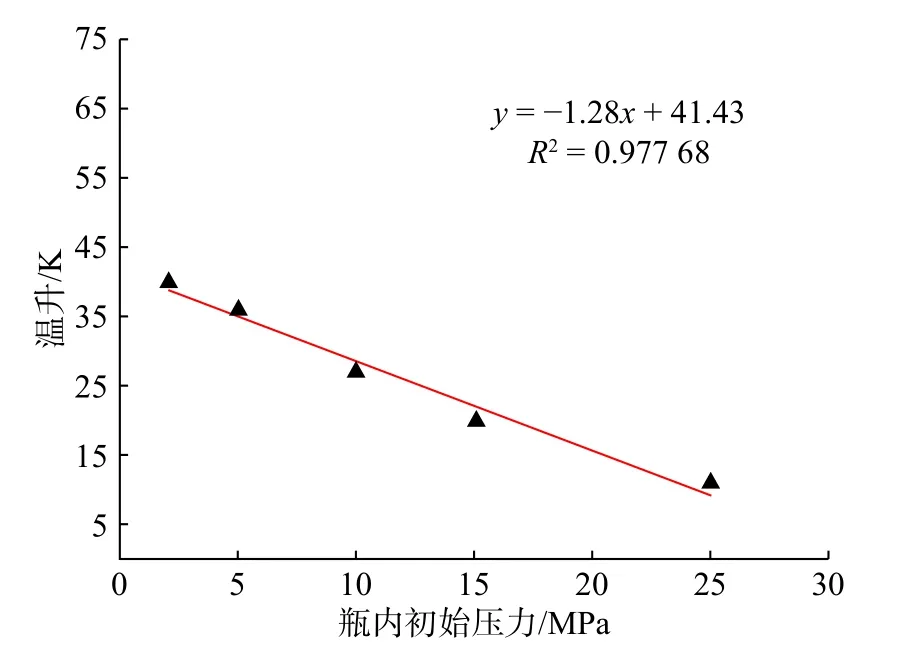
图8 瓶内初始压力对快充温升的影响规律Fig.8 Influence law of initial pressure in bottle on rapid temperature rise

4 结论

本文以CNG 快速充装为例，讨论玄武岩纤维增强35 MPa 气瓶在快速充装过程中的温升效应，对实际充装过程进行了一定简化和假设，在此基础上分析了气瓶温升效应的理论模型与计算方法，从仿真层面探究了不同充装因素与气瓶温升效应的关系，建立了2 维轴对称气瓶有限元模型，利用Fluent 流体力学软件分析了5 min 内将气瓶初始压力从2 MPa 升至35 MPa 过程中的温升效应，得到了不同时刻的气瓶内部温度分布云图，分析了影响温升效应的主要因素，得到以下结论。

1）在设定的边际条件下，经过5 min 的快速充装，气体最高温度达到333 K（60 ℃），温升为40 K，符合ISO 11439– 2013 标准规定，表明利用玄武岩纤维制备的35 MPa 级CNG 气瓶，在快速充装时不会因玄武岩本身的低导热率出现危险，将该产品应用于CNG 汽车可行。

2）气瓶快速充装温升效应主要与充装时间、瓶内初始压力和环境温度有关。在本文设定的讨论条件下，瓶内初始压力对气瓶温升影响较小，而充装时间小于100 s，环境温度高于305 K（32oC）时，将给35 MPa 玄武岩纤维增强复合材料气瓶带来明显的温升效应，缩短其使用寿命。