基础隔震结构的运动方程与阻尼矩阵在动力响应分析中的适用性研究
李世渊,谭 平,2,3,马海涛,2,3
(1.广州大学 土木工程学院,广州 511442;2.广州大学 工程抗震减震与结构安全重点实验室,广州 510405;3.广州大学 广东省地震工程与应用技术重点实验室,广州 510405)
运动方程和阻尼模型是结构动力分析算法的基础,其合理性和适用性对计算精度有关键性影响,因此值得予以高度重视。基础隔震结构由上部结构和含有隔震支座的隔震层组成,由于其隔震层的刚度一般远低于上部结构,隔震支座会发生可观的变形,引起上部结构较大幅度的刚体运动;另一方面,隔震支座一般都具有较高的阻尼,因此其使用可达到消耗能量、降低振动响应的目的。鉴于基础隔震结构的特殊性,常规结构动力分析方法对其是否仍然适用以及这些方法的计算精度是值得研究的问题。
结构抗震时域动力分析常用的运动方程有两种形式,其中的一种基于地震动加速度输入以结构相对位移为未知量,另一种基于地震动位移输入以结构绝对位移为未知量,与这两种运动方程对应的两种分析模型分别被称为加速度输入模型和位移输入模型[1-2]。加速度输入模型是考虑一致地震动作用时最常用的模型,被广泛地用于结构分析计算和设计;事实上,真实地震动是随着空间不断变化的,这一特性将会导致结构各支承点激励出现显著差异,由其对大跨结构的动力响应具有明显影响,此时一致加速度模型不在适用,而应采取适用于多点输入的计算模型或方法[3-4]。位移输入模型较易于用于考虑多点激励情况,因此成为计算结构非一致地震动作用下动力响应的常用模型[5-7];值得指出的是,位移输入模型不仅适用于非一致地震动作用下动力响应,同时也适用于一致地震动作用下动力响应。田玉基等[1]采用位移输入模型和加速度输入模型进行了单自由度无阻尼体系的时域分析,研究了时间步长对计算精度的影响,得到同一时间步长情况下位移输入模型计算精度较高的结论。柳国环等对位移输入模型和一致加速度模型进行了分析比较,认为两者本质上存在差别,因此会导致计算结果的不同。国巍等[8]研究了考虑多点激励的隔震结构分析模型,探讨了加速度模型和位移模型中的阻尼定义以及计算误差和适用性等问题,提出了通过计入阻尼项构造的修正位移模型和修正加速度模型,并建议对于实际结构模型可能产生的误差做进一步研究。何卫平等[9]针对水工大坝结构研究了位移输入模型在地震响应分析中的适用性问题,分析了位移与加速度输入模型间的差异,提出采用位移输入模型时必须判断其给出结果的误差水平,避免计算精度不满足要求的情况。
常规结构的阻尼模型已有大量的研究,针对不同情况提出了各种模型;例如,对于非比例阻尼结构,可在分别生成各部分的阻尼矩阵之后进行组装形成结构的总体阻尼矩阵[10]。而针对隔震结构阻尼矩阵的相关研究则还非常有限,目前一般采用的是适用于普通非比例阻尼结构的方法,亦即按常规方法生成上部结构的阻尼矩阵,然后直接将其与隔震系统的阻尼矩阵叠加形成总体阻尼矩阵[11]。国巍等在考虑多点激励的隔震结构分析模型的研究中提出位移模型和加速度模型的阻尼特性不一致的问题。周国良等[12]讨论了一致激励与多点激励情况下基底大质量法和支座强迫位移法的适用性问题,分析了应用Rayleigh阻尼模型计算阻尼力的差别,并提出了修正算法。
值得注意是,常用的地震响应分析模型中,位移输入模型所采用的运动方程建立在结构阻尼作用比较小的假设条件基础之上,是通过忽略与结构阻尼和地震动速度相关的等效荷载而得到的。尽管对于低阻尼常规结构,位移输入模型通常可以给出满足精度要求的分析结果,但对于隔震结构,高阻尼隔震支座的应用使得假设条件不再成立,而且随着支座阻尼的提高,被忽略的部分等效荷载所产生的误差将会增大,不可避免地影响计算精度。Wilson[13]认为与地震动速度相关的等效荷载因为相关联的阻尼矩阵无法确定,所以也有必要将其忽略,进而得到位移输入模型。相比之下,加速度输入模型则没有此类限制条件,理论上其计算精度与结构的阻尼特性无关。
目前隔震结构的分析一般采用将上部结构与隔震系统的阻尼矩阵直接叠加生成总体阻尼矩阵的方法,而且通常对上部结构采用Rayleigh阻尼模型,例如文献[11]。但这样做会产生一个后果:上部结构在随隔震支座发生刚体位移时将会产生阻尼力,而这显然与实际情况是不符的。
基于以上讨论,本文将针对隔震结构研究阻尼模型和地震动输入模型对动力分析计算精度的影响规律,提出相应的解决方法。本文从常规结构的运动方程出发,采用不同形式绝对或相对位移变量,推导对应的隔震结构运动方程,再基于隔震结构的变形特性和上部结构中阻尼力分布应满足的条件,提出隔震结构阻尼矩阵的通用表达式。采用隔震结构简化模型,给出动力分析所涉及的全部结构矩阵的解析表达式,并以此为基础进行算例验证,详细分析阻尼模型和地震动输入模型对隔震结构计算结果精度的影响,最后给出结论和建议。
1 隔震结构理论模型
1.1 一般结构运动方程
多自由度结构在(一致)地震作用下的运动方程可表示为以下形式
(1)
式中:M、C和K表示结构总体质量矩阵、阻尼矩阵和刚度矩阵;ur(t)表示结构相对基础运动的位移向量;ug(t)表示基础位移;E为地震动影响向量E=[1,1,…1]T;标识符上的一点和两点表示对时间的一阶和二阶导数。
采用(1)式给出的运动方程以及适当的初始条件,我们可以根据地震动加速度时程确定结构的相对位移,进一步确定结构动力响应。对应的计算模型常被称为加速度输入模型。用ut(t)表示结构的总体位移向量,则对应的相对位移向量ur(t)可表示为
ur(t)=ut(t)-Eug(t)
(2)
将式(2)代入式(1),整理后可得
(3)
方程右端的两项依次表示对应于地震动速度和位移的等效荷载。值得指出的是,式(3)与式(1)给出的运动方程尽管形式不同和需要采用不同的地震动时程作为输入,但理论上完全一致。当输入的地震动数据一致并且结构初始条件相同时,两种形式的运动方程的解应完全一致;若不计数值误差,两个解应严格满足式(2)。
对于常规结构,结构阻尼作用相对较小,式(3)给出的运动方程右端与地震动速度相关的等效荷载通常可以忽略不计,此时运动方程可改写为
(4)
以此为基础,可以得到相应的位移输入模型,并根据适当的初始条件和地震动位移时程确定结构的绝对位移。
尽管位移输入模型在结构地震响应计算中已经获得了成功应用,但对于隔震结构,可否在运动方程中忽略与地震动速度相关的一项是一个被轻视的问题,目前还缺乏对位移输入模型有效性和计算精度的深入系统研究。另一方面,与地面运动速度相关的右端项和隔震结构阻尼矩阵有关,位移输入模型的误差问题本质上是阻尼问题。而位移-速度输入模型有效克服了位移输入模型存在的问题,保留了与地面运动速度相关的阻尼耦合项,但由于通常认为此项无法确定,导致位移-速度输入模型的使用受到了限制。
由上述分析可知,隔震结构的阻尼矩阵对地震动输入模型合理使用起着重要的作用。鉴于目前形成隔震结构阻尼矩阵的方法存在一定的缺陷,本文将首先对隔震结构阻尼矩阵进行理论推导,提出了为得到准确结果需要采用形成隔震结构阻尼矩阵的方法和理论依据,得到了关于隔震结构阻尼矩阵的通用表达式。在此基础上,研究采用不同的地震动输入模型对隔震结构响应的影响规律。
1.2 隔震结构运动方程
考虑一个上部结构具有n个自由度的隔震结构,并假设其相对基础运动的位移向量ur(t)可以记为
(5)
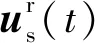
(6)
式中:下标为ss的子矩阵维数为n×n;下标为sb的子矩阵维数为n×1(即n阶列向量);下标为bs的子矩阵维数为1×n(即n阶行向量)。因为矩阵的对称性,三个矩阵中下标为sb的子矩阵等于对应的下标为bs的子矩阵的转置。隔震层的质量、刚度和阻尼常数可依次记为mb、kb和cb,隔震结构的质量矩阵、刚度矩阵和阻尼矩阵可表示为以下形式
(7)
应该指出的是,式(6)中的上部结构质量和刚度矩阵可采取与常规结构动力分析同样的方式确定,其中的Mss和Kss分别表示上部结构在隔震层位移固定状态下的质量和刚度矩阵。但是,由于隔震层的存在,相对位移向量中将包含对应于上部结构随隔震层变形时刚体位移的成分,因此式(6)中的上部结构的阻尼矩阵应与常规结构动力分析情况下的阻尼矩阵不同。我们将在下一节具体讨论这一问题。
对于上部结构,引入相对隔震层的位移向量us(t)=ur(t)-ub(t)Es,其中,Es为影响向量E中与上部结构相关的前n个分量构成的列向量。此时可定义隔震结构相对隔震层的位移向量如下
(8)
于是,相对基础运动的位移向量ur(t)可以表示为
ur(t)=Tu(t)
(9)
其中,T为下式给出的转换矩阵
(10)
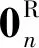
(11)
式中的M*、C*、K*和Q*分别为下式给出的矩阵或向量
M*=TTMT,C*=TTCT,
K*=TTKT,Q*=-TTME
(12)
将式(7)和(10)代入式(12),可得
(13)
引入的子矩阵和变量分别为
(14)
1.3 隔震结构阻尼矩阵
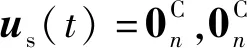
(15)
另一方面,依据(11)式中的运动方程,子矩阵Kss和Css应为上部结构在隔震层位移固定状态下的刚度和阻尼矩阵,也就是上部结构的常规阻尼矩阵。
(16)
至此,我们确定了上部结构对隔震结构总体阻尼矩阵的贡献,即式(6)中的矩阵Cu,将其代入式(7),可得隔震结构的阻尼矩阵的表示式如下
(17)
很明显,隔震结构的阻尼矩阵由上部结构阻尼矩阵子块Css、隔震层阻尼cb和影响向量Es完全确定。而与此对应地,我们有
(18)
(19)
显然此式给出了合理的隔震结构的阻尼力分布。
对于上部结构阻尼矩阵可采用Rayleigh阻尼模型和Caughey阻尼模型来形成,采用Rayleigh阻尼模型时,上部结构阻尼矩阵可表示为
Css=αMss+βKss
(20)
上部结构阻尼矩阵采用Caughey阻尼模型来形成时,Css可表示为
(21)

假若直接采用Rayleigh阻尼模型计算上部结构对隔震结构阻尼矩阵的贡献,也就是取Cu=αMu+βKu,隔震结构的阻尼矩阵为
(22)
式中,Css=αMss+βKss。显然,式(22)与由式(17)给出的阻尼矩阵明显不同,而且当上部结构随隔震层发生刚体位移时,据此得到的隔震结构阻尼力向量为
(23)
这比式(19)中的表达式多出与上部结构的质量矩阵和质量阻尼系数相关的一项,当质量阻尼系数α≠0时,对上部结构给出了非零的结构阻尼力,明显与实际情况不符,说明直接采用Rayleigh阻尼模型计算上部结构对隔震结构阻尼矩阵的贡献是不恰当的。我们将用数值算例结果证明这一做法可能产生较大的计算误差。
2 隔震结构分析方法
至此,我们得到了隔震结构阻尼矩阵的一般表达式。基于这一表达式给出的阻尼矩阵,可以采用不同的地震动输入模型进行隔震结构分析。本文将考虑以下三种分析算法:
算法 1:采用加速度输入模型,利用式(1)中的运动方程以及初始条件,根据地震动加速度求解位移向量ur(t),或者基于(11)式求解位移向量u(t);
算法 2:采用位移输入模型,利用式(4)中的运动方程以及初始条件,根据地震动位移求解位移向量ut(t);
算法 3:采用位移-速度输入模型,利用式(3)中的运动方程以及初始条件,根据地震动位移和速度求解位移向量ut(t);
算法1和算法2实际上是结构地震响应计算中常采用的方法。由于隔震支座一般具有较高的阻尼,而位移输入模型在运动方程中忽略了与地面运动速度相关的右端项,因此算法2用于隔震结构分析存在潜在的计算精度问题,还需考察研究。相比之下,位移-速度输入模型保留与地面运动速度相关的右端项,与加速度输入模型在理论上一致,有效克服了位移输入模型自身的缺陷。
3 隔震结构简化模型
本文的讨论至此未对隔震结构的具体形式加以限制,所以理论推导结果适用于一般隔震结构。为方便起见,接下来我们将考虑图1所示的剪切型简化模型,这样我们可以给出涉及到的全部结构矩阵具体的解析表达式。
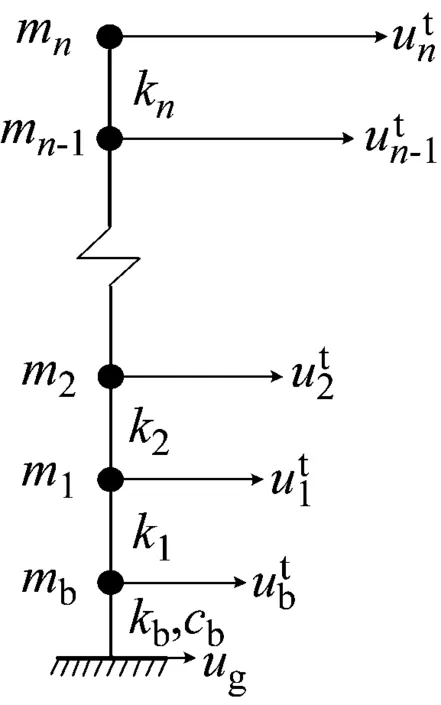
图1 基础隔震结构剪切型模型Fig.1 A shear-type modelof base-isolated structures
首先,对于上部结构的质量矩阵和刚度矩阵,可表达为
(24)
对于上部结构的阻尼矩阵,采用Rayleigh阻尼模型时,有Css=αMss+βKss。注意此时影响向量E为全部元素皆等于1的n+1维向量。由式(15)和(16),可得阻尼矩阵子块Csb和Cbb的表达式
Csb=-αms-βks,Cbb=αmstot+βk1
(25)
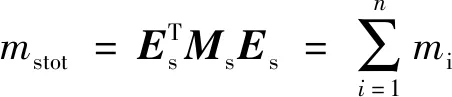
(26)
假若直接采用Rayleigh阻尼模型计算上部结构对隔震结构阻尼矩阵的贡献,则阻尼矩阵子块Csb和Cbb的表达式为
(27)
对比式(25),可以发现上式中缺少了与上部结构质量相关的部分。
至此,我们得到了采用隔震结构剪切型简化模型进行动力分析所需要的基本矩阵的解析表达式。将以上表达式代入式(14),可得到式(11)中运动方程的系数矩阵,进一步可验证它们与文献[14]采用的表达式完全一致。
4 算例分析与结果讨论
为研究不同分析模型的计算精度,本节给出了两个隔震结构的动力时域分析典型算例,算例抗震设防烈度均为8度,II类场地,设计地震分组为第二组,场地特征周期为0.4 s,设计基本加速度为0.2g。通过数值结果的总结和对比,着重研究隔震结构阻尼矩阵的形成方式和地震动输入模型对计算精度的影响:
(1) 隔震结构阻尼矩阵的形成方式:用Rayleigh阻尼模型和Caughey阻尼模型表示上部结构的阻尼特性,采用Rayleigh阻尼模型时,分别应用1.3节讨论的两种方法计算上部结构对隔震结构阻尼矩阵的贡献,亦即直接计算或根据本文提出的方法进行计算;
(2) 地震动输入模型:采用第2章列出的三种地震动输入模型,亦即常规的加速度输入模型和位移输入模型,以及位移-速度输入模型。
为进行隔震结构的动力时域响应分析,从加利福尼亚大学伯克利分校太平洋地震工程研究中心(PEER)的数据库中选取了四条地震波,相关信息如表1所示。具体的位移、速度和加速度时程皆可从PEER的网站(https:∥peer.berkeley.edu/)下载获得。在计算过程中,将4条波的地震动加速度幅值调至设计地震动加速度规定值(0.2g),对应的速度和位移时程亦可通过加速度调幅比例进行调整。图2给出了4条波反应谱与规范反应谱对比情况。

表1 地震波记录信息Tab.1 Ground motion records information
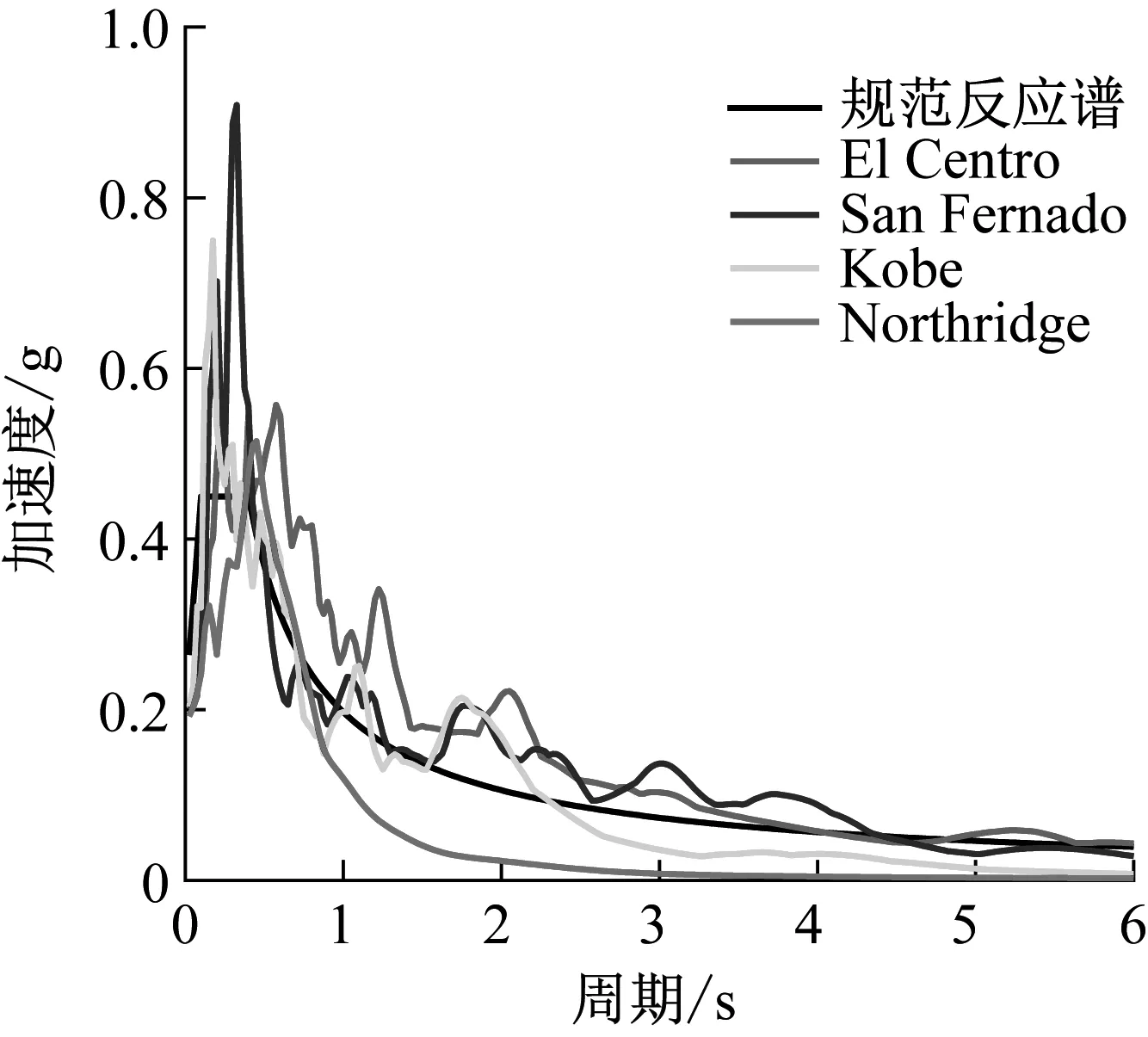
图2 地震动反应谱与规范反应谱对比Fig.2 Comparison of the code design spectrum and the spectrum of the 4 natural ground motions
动力时域分析将采用Newmark-β逐步积分法,积分步长取为地震波记录的时间步长。对于剪切型隔震结构模型,上部结构的层间位移决定着变形和内力的大小,而隔震支座变形也是分析设计中主要关注的响应量。因此,在算例结果中仅考虑上部结构层间位移和隔震层相对位移。
4.1 单层隔震结构模型算例
首先考虑一个将上部结构简化为单自由度子系统的双自由度基础隔震结构模型,上部结构与隔震层的质量、刚度和阻尼参数如表2所示[15]。上部结构的临界阻尼比为0.05,而隔震层等效阻尼比ξb=0.3。
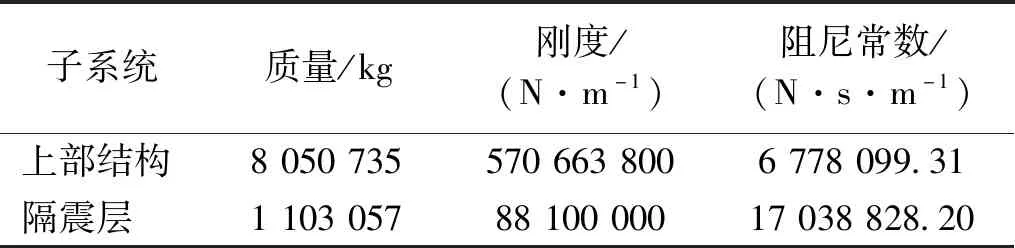
表2 单层隔震结构模型质量与刚度数据Tab.2 Mass and stiffness data for the one-story base-isolated model
首先考虑El Centro波,分别采用三种算法进行时域响应分析。图3给出了上层结构层间位移和隔震层相对位移时程结果,从中可以看出,加速度输入模型和位移-速度输入模型给出的相对位移时程曲线高度吻合,而位移输入模型结果则有很大的偏差。再考虑另外三条地震波,分别采用三种算法进行时域响应分析,得到的时程结果同样具有以上特征。为节省篇幅未给出对应的位移时程曲线,但在表3给出了不同算法给出的最大相对位移结果,以及用加速度模型的结果作为参考解时的相对偏差。可以发现,对于全部四条地震波,加速度输入模型和位移-速度输入模型的结果均高度一致,相对偏差不超过0.1%;但位移输入模型全都高估隔震层位移、低估上部结构的层间位移。很明显,因为位移输入模型的运动方程没有考虑与地震动速度相关的等效荷载项,结果导致较大的误差。
容易理解,位移输入模型给出的结果的误差与地震激励有关,因此响应结果的相对偏差可能在一个较大范围内变化。对于采用的四条地震波,隔震层最大相对位移结果的偏差范围为3.5%~31.0%,而最大层间位移结果的偏差范围为14.2%~49.5%。特别值得注意的是,对于Northridge波,尽管隔震层相对位移偏差仅为3.5%,上层结构层间位移相对偏差达到了近50%。对隔震层位移时程结果进行分析后发现,虽然位移输入模型给出的最大值相对偏差不大,具体时程还是有显著的差别,所以造成上部结构最大层间位移结果有很大偏差。表3中最后一列中的数据说明,上部结构层间相对位移和隔震层相对位移的结果偏差不成比例,因此仅仅通过比较隔震层相对位移最大值是否接近来判断隔震结构分析结果的精度是不够的。
4.2 五层隔震结构算例
考虑文献[11]中的五层隔震结构模型,上部结构的临界阻尼比设为0.05,隔震层的等效阻尼比ξb=0.21,其上部结构和隔震层的质量与刚度分布如表4所示。
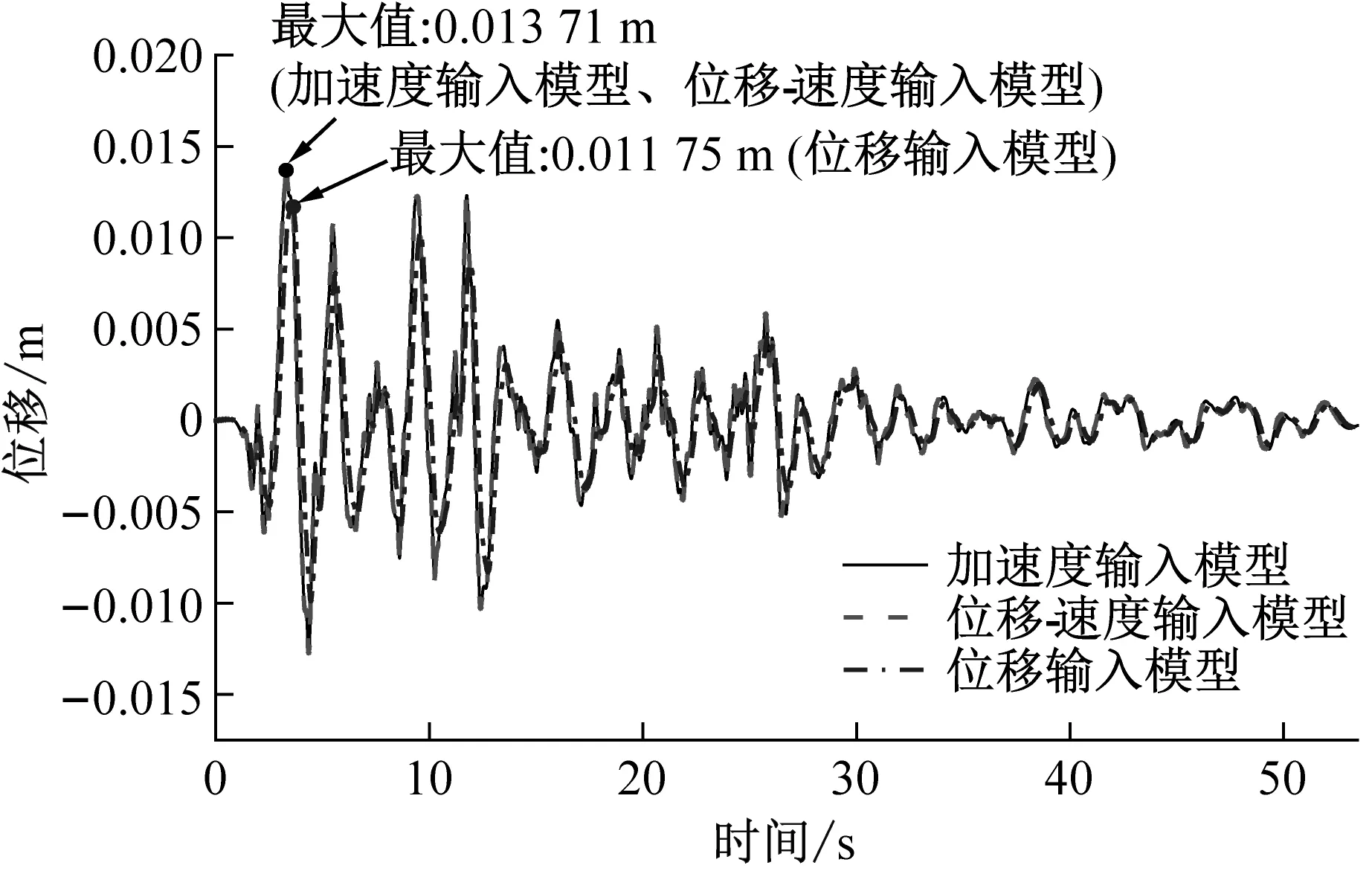
(a) 上部结构
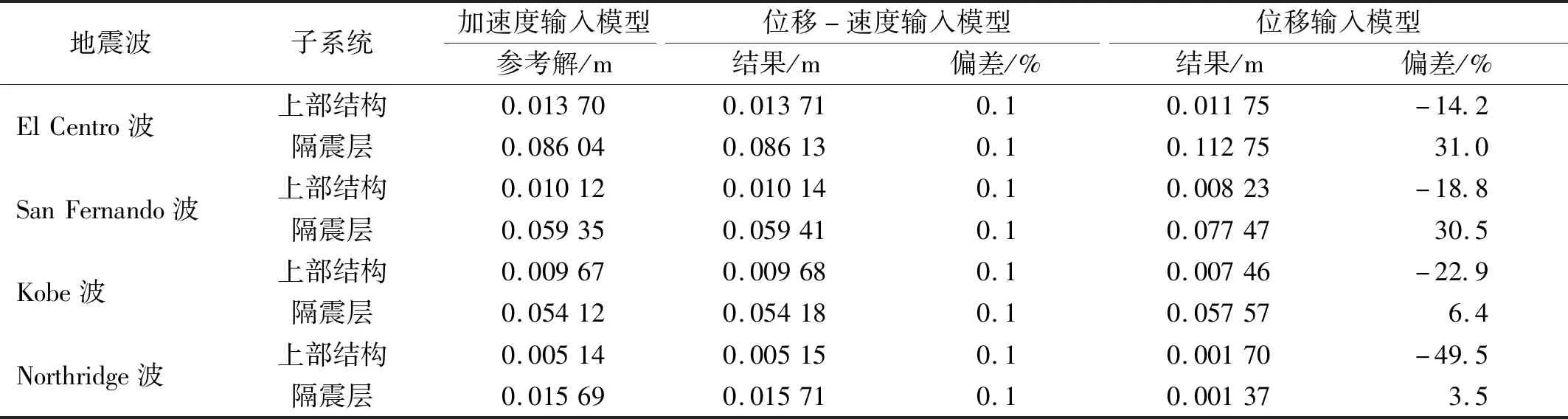
表3 单层隔震结构最大相对位移结果Tab.3 Maximum relative displacement results of one-story base-isolated model
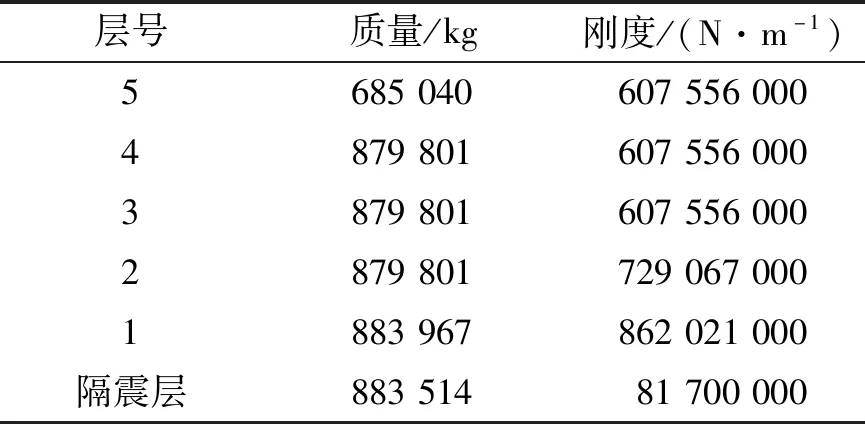
表4 五层隔震结构质量与刚度数据Tab.4 Mass and stiffnessdata for the five-story base-isolated model
我们将采用Rayleigh阻尼构造上部结构阻尼矩阵。计算得到整体结构的前两阶固有频率分别为ω1=3.71 rad/s和ω2=15.46 rad/s,命对应的模态阻尼比为0.05,可计算得到质量和刚度阻尼系数为α=0.299 0,β=0.005 2。
分别采用三种算法和El Centro波进行隔震结构的时域响应分析。表5给出了不同分析模型给出的最大相对位移和偏差。可见位移-速度输入模型与加速度输入模型的结果高度一致,而位移输入模型高估隔震层位移、低估上部结构的层间位移,最大相对偏差达到近20%,再次说明位移输入模型不适用于隔震结构。
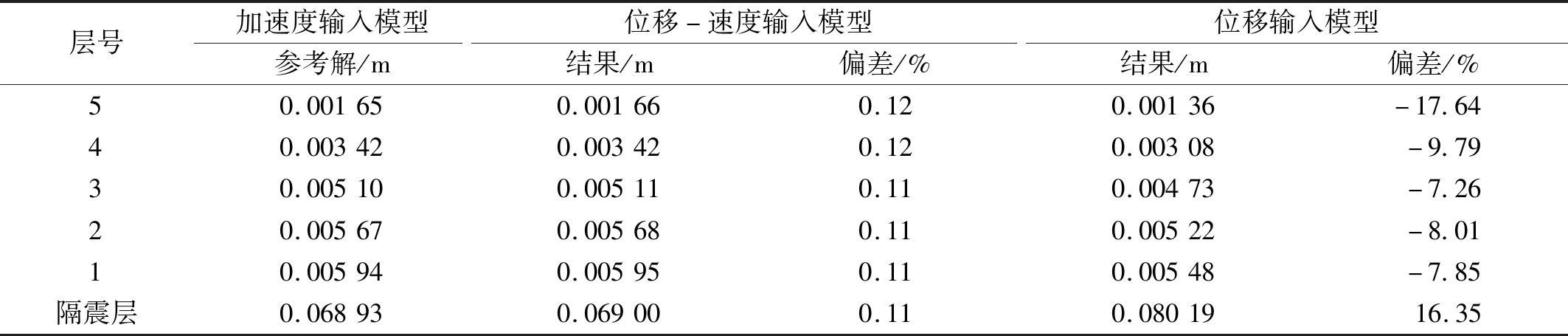
表5 五层隔震结构最大相对位移结果 (ξb=0.21)Tab.5 Maximum relative displacement results of the five-story base-isolated model (ξb=0.21)
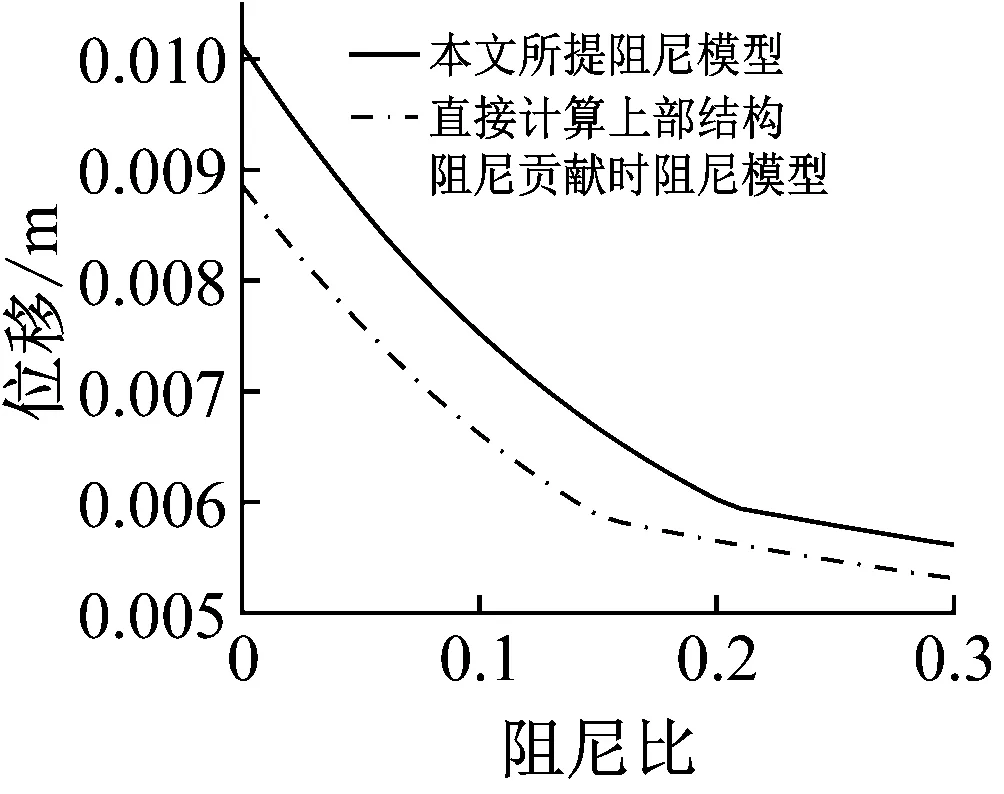
为了考察隔震结构阻尼矩阵采用不当对分析结果的影响,我们采用直接考虑上部结构对隔震结构阻尼矩阵贡献的算法重复进行分析,并将结果总结于表6。表中数据显示,加速度输入和位移-速度输入模型给出的结果接近,隔震层位移和上部结构层间位移结果都明显偏低,上部结构最大偏差达到了5.56%,隔震层最大相对偏差达到了8.39%。由此可见,对于隔震结构,直接考虑上部结构对隔震结构阻尼矩阵贡献的方法会低估结构的变形。
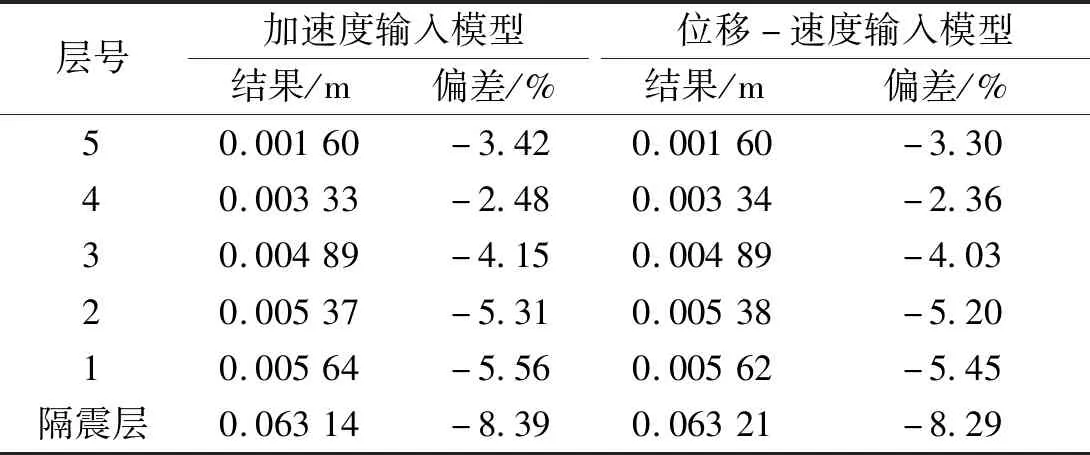
表6 直接计算上部结构阻尼贡献时五层隔震结构最大相对位移结果(ξb=0.21)Tab.6 Maximum relative displacement results of the five-story base-isolated model when the damping of superstructure is used directly (ξb=0.21)
为了考察不同隔震层阻尼比情况下不同计算模型的精度,可将隔震层的等效阻尼比范围取为0~0.3[16]。
首先考虑在不同阻尼模型下对隔震结构动力响应的影响,为了比较不同阻尼矩阵下的隔震结构响应差异,分析时均采用一致加速度输入模型,并将结果总结于图4中。从图4中可以发现,在不同隔震层等效阻尼比情况下,直接采用Rayleigh阻尼模型计算上部结构阻尼贡献时,隔震结构的相对位移明显偏低,均低估了隔震结构的响应,其中,底层层间位移最大相对偏差为5.38%~12.47%,顶层层间位移最大相对偏差为2.83%~15.77%,隔震层相对位移最大相对偏差为5.14%~13.95%;另一方面,随着隔震层等效阻尼比的增大,直接采用Rayleigh阻尼模型计算上部结构阻尼贡献时的计算相对偏差随之减小。这是因为,直接采用Rayleigh阻尼模型计算上部结构阻尼贡献时的阻尼矩阵与本文所提阻尼矩阵的不同之处在于缺少了与上部结构质量相关的部分。当隔震层阻尼比较小时,此项对隔震结构的响应影响起主要作用,因此采用直接计算上部结构阻尼贡献时阻尼模型计算的相对偏差较大,随着隔震层等效阻尼比增大,隔震层等效阻尼系数增大,此时隔震层等效阻尼系数将对隔震结构响应的影响起主要作用,与上部结构质量相关的部分对隔震结构响应的影响减弱,相对偏差随之减小。
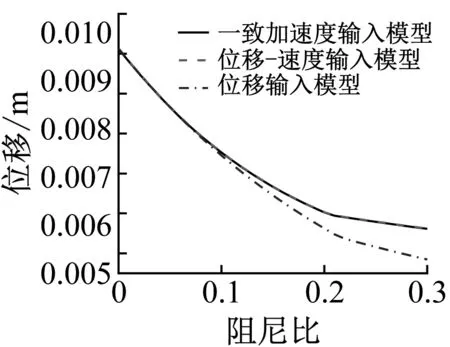
另一方面,考察隔震结构在不同隔震层等效阻尼比情况下,采用第2章提到的隔震结构分析方法分析隔震结构动力响应。值得注意的是,在此部分分析中采用的阻尼矩阵均是本文所提阻尼矩阵,以避免其它不相干因素对分析结果产生影响。分别采用Rayleigh阻尼和Caughey阻尼构造上部结构阻尼矩阵,进行分析计算,并将结果总结在图5~图7中。可以发现,随着阻尼比的增大,无论是采用Rayleigh阻尼还是Caughey阻尼构造上部结构阻尼矩阵,采用位移输入模型得到的结果偏离参考解的程度都不断加剧。当隔震层等效阻尼比达到0.3时,采用位移输入模型仍然还是会高估隔震层位移、低估上部结构的层间位移,相对偏差可达到34.6%和-31.1%。
(a) 底层
(a) Rayleigh阻尼
应用其它三个地震波重复进行五层隔震结构模型的分析,所得到的结果反映出基本相同的规律:首先,加速度输入和位移-速度输入模型结果吻合良好,而位移模型的偏差较大并随隔震层阻尼的增高而增大;其次,直接考虑上部结构对隔震结构阻尼矩阵贡献会显著地高估上部结构的阻尼,造成较大的计算误差。研究中,还采用文[11]中的九层隔震结构模型进行了分析计算,结论相同。因篇幅所限,文中未给出具体数值结果。
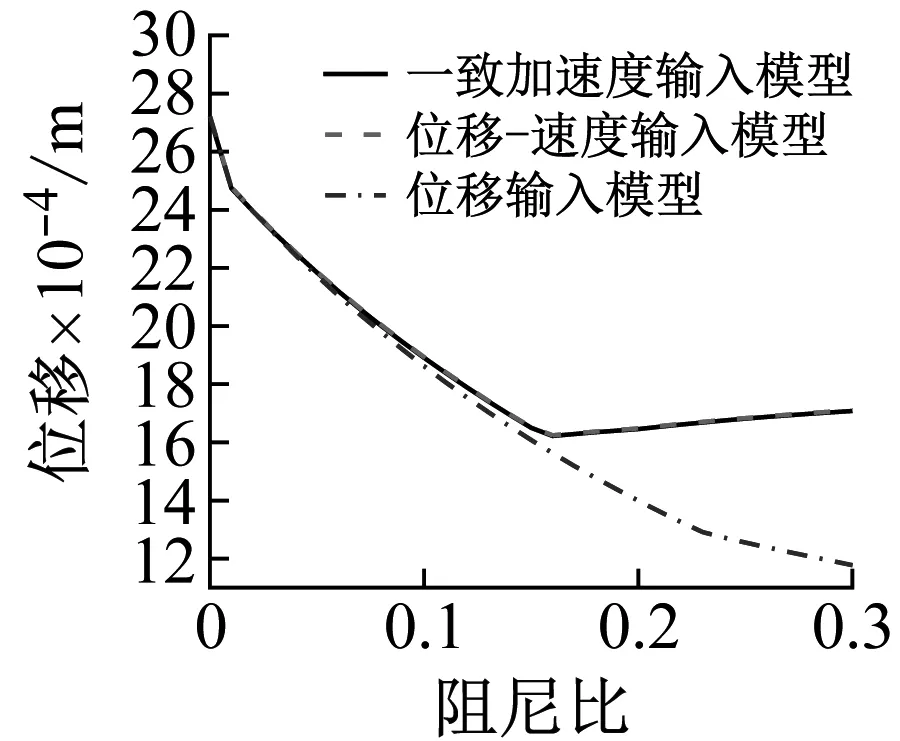
(a) Rayleigh阻尼
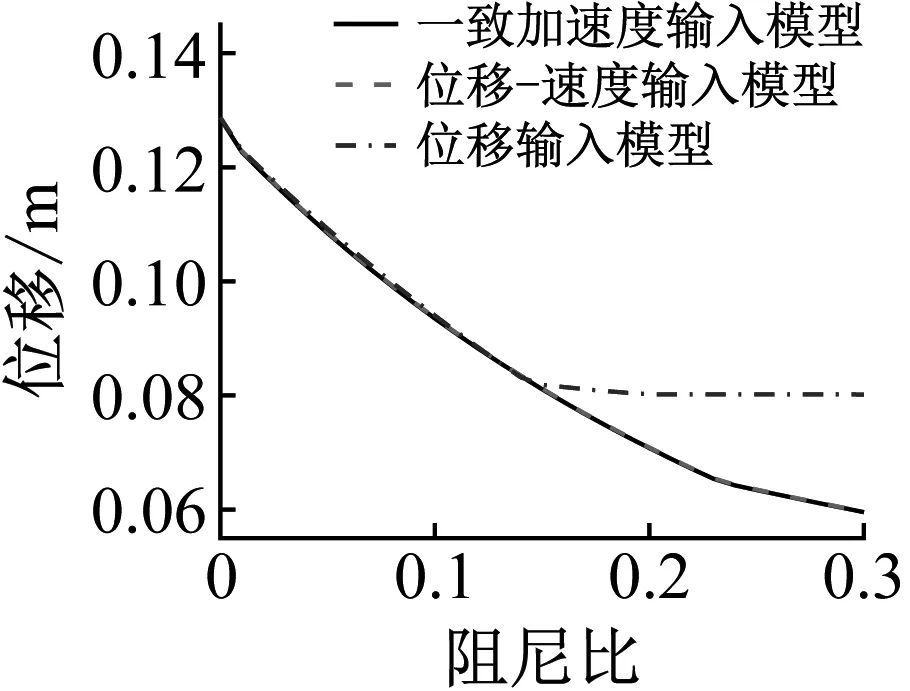
(a) Rayleigh阻尼
5 结 论
本文研究了基础隔震结构的分析方法,着重考虑了阻尼矩阵的形成和地震动输入模型对动力响应分析算法精度的影响,主要结论如下:
(1) 为了在基础隔震结构的动力时域分析中准确考虑高阻尼支座的影响,应采用位移-速度输入模型替代传统的位移输入模型。
(2) 位移输入模型并不适用于基础隔震结构,尤其是在采用高阻尼隔震支座的情况下计算结果会有较大误差。这是因为,采用位移输入模型需忽略结构与支承点相关联节点间的耦合阻尼对应的等效荷载,当阻尼比越大时,此项对结构响应的影响也越大,导致相对误差越大。算例结果表明,位移输入模型给出的结果一般会高估隔震层变形、低估上部结构响应,最大相对偏差可超过30%。
(3) 直接采用Rayleigh阻尼计算上部结构对隔震结构阻尼矩阵的贡献时,会错误地引入附加结构阻尼,算例表明这样会严重地低估结构响应。
(4) 文中提出了形成隔震结构阻尼矩阵的方法,可用于正确地模拟结构的阻尼性质,采用此方法可保证位移-速度输入模型和加速度模型给出一致的计算结果,这是因为,两种输入模型尽管形式不同,但理论上完全一致,当输入的地震动数据一致并且结构初始条件相同时,两种形式的输入模型的解应完全一致。
研究中仅考虑了一致地震动激励情况,在数值计算中采用了剪切型模型,对于更一般的情况还需要进行相应的数值计算、展开进一步研究。

