饱和混凝土冲击破坏的近场动力学建模分析
武立伟,马启鹏,黄 丹
(河海大学 力学与材料学院,南京 211100)
混凝土作为一种多相复合材料,具有良好的易成形性、抗水耐火性、耐久性以及原料充沛、价格便宜等优点,在诸多工程领域得到广泛应用。在工程实际中,较大部分混凝土结构长时间处于水环境中,如大坝、桥墩、渡槽以及各种近海建筑物等。同时,由于混凝土存在各种微裂纹以及孔隙,在长时间外界水压力作用下,混凝土湿度升高,其力学性能也会发生改变,导致饱和混凝土材料与结构的力学性能与干燥状态下大为不同,有必要开展专门的饱和混凝土力学行为研究。
近年来,随着计算机技术的快速发展,对于混凝土破坏问题的研究多采用理论、实验与数值模拟相结合的方法。对混凝土动态冲击下损伤破坏过程的精确模拟一直是多领域关注的焦点和难题。针对动态破坏问题,现有数值方法大多基于经典连续介质力学理论,但经典连续介质力学理论中“连续性”假设与实际情况相矛盾,需要引入外部准则或者进行特殊处理,往往导致在计算精度和计算效率方面遇到瓶颈。已有众多研究者提出了各种处理不连续区域奇异性和网格重构的特别措施[1-5],但在处理动态冲击破坏以及裂纹扩展等复杂问题时,依然面临困难和挑战。
为从根本上解决基于连续性假设的传统数值方法在模拟不连续力学问题时的困难,2000年Silling首次提出了非局部近场动力学(Peridynamic,PD)理论[6-7],基于非连续性假定建模,以空间积分型运动方程替代传统连续介质力学的空间微分型运动方程,适用于物体连续或不连续的任何区域,突破了传统连续介质力学理论和方法在求解不连续力学问题时的瓶颈。另外,近场动力学模型中包含了对损伤与断裂的描述,对于动态裂纹扩展、冲击破坏等不连续且非局部效应显著的问题表现出独特优势[8-12]。
目前,已有众多国内外学者采用近场动力学方法对混凝土断裂破坏问题进行研究,Gerstle等[13]模拟分析了混凝土和钢筋混凝土结构在拉、压、剪荷载条件下的渐进破坏过程;Huang等[14]提出了一种新的力加载方法,通过引入局部阻尼准静态求解算法和不平衡力收敛准则,建立了更精确的近场动力学混凝土模型;顾鑫等[15-16]对混凝土的冲击破坏以及侵彻过程进行了研究;Wu等[17]考虑混凝土率敏感性,提出一种率相关的近场动力学模型,并应用于混凝土动态断裂问题;Chen等[18]提出一种热力耦合模型,模拟了混凝土中热扩散、热致变形和断裂过程。为了克服均质化模型的不足,Li等[19]提出了考虑混凝土细观结构的多尺度模型,并进行了验证,但由于计算成本巨大,该模型仅限于准静态载荷下的二维数值模拟。
在现有研究基础上,本文提出一种考虑孔隙作用的亚均质[20]近场动力学饱和混凝土模型,分析动态载荷条件下饱和混凝土的力学行为。该模型考虑混凝土细观结构的非均质性以及混凝土结构内部的孔隙作用,并基于两相球模型得到饱和混凝土中水泥砂浆的有效体积模量与剪切模量。通过对混凝土板波传播过程以及靶板冲击破坏试验数值结果与试验结果进行比较,验证了该模型和方法对于研究饱和混凝土动态力学行为和冲击破坏问题的适用性。
1 常规态型近场动力学理论
态型近场动力学理论[21]基本思想如图1所示,物质点x受到其近场范围内所有其它物质点作用,根据牛顿第二定律可得运动方程为
(1)


图1 物质点间的相互作用Fig.1 Non-local interaction between material points


(2)


(3)
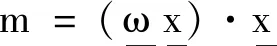
(4)
(5)

常规态型近场动力学理论的核心是借鉴连续介质力学张量分解思想,将拉伸标量状态和力标量状态分解为球量部分和偏量部分,两者可以完全解耦,具体为
(6)
(7)


(8)
类比传统连续介质力学中应变能密度形式,构建常规态型近场动力学中三维线弹性固体材料的应变能密度为
(9)
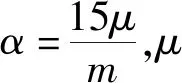
将式(9)代入式(8)可以得到力标量状态表达式为
(10)
2 考虑孔隙作用的亚均质饱和混凝土模型
2.1 亚均质近场动力学模型
亚均质近场动力学模型作用在“键”层次上,即通过定义不同种类的“键”来表征混凝土细观尺度的各相成分。如图2所示,混凝土被视为由三相成分组合而成(骨料、砂浆基体、界面过渡区)。任意“键”连接两个物质点,其位置可以处于骨料区或砂浆区或界面过渡区,两物质点可以处于同一相区域,也可以处于不同相区域,从而根据物质点位置定义“键”的类型,不同“键”出现的概率只取决于各相成分的体积分数。另外,在判定每一个“键”类型时是根据生成的随机数确定的,即不同类型的“键”完全随机分布,各相成分的实际分布情况并没有考虑到亚均质模型中,因而图2中界面过渡区没有在骨料周围而是独立随机分布。

图2 亚均质模型不同“键”类型示意图Fig.2 Schematic of different bond types of IH-PD model for concrete material
考虑混凝土的三相成分,因此共有六种类型的“键”,包括三种“成分键”(两物质点处于同一相区域中)和三种“界面键”(两物质点处于不同相区域中)。定义六种“键”分别为A-A“键”(骨料),C-C“键”(砂浆),I-I“键”(界面过渡区),A-C“键”(骨料-砂浆),A-I“键”(骨料-界面过渡区),C-I“键”(砂浆-界面过渡区)。
本文假设混凝土材料在宏观尺度上是均匀的,因此各相成分的体积分数是固定不变的,各种类型“键”的比例也仅取决于各相成分的体积分数。一旦确定了“键”的类型,相应成分的材料参数(如密度、弹性模量、断裂能等)就可以分配给它。对于三种“成分键”,A-A“键”,C-C“键”和I-I“键”分别对应骨料、砂浆以及界面过渡区的物质属性。考虑到“界面键”有三种类型,假设A-C“键”的力学性能与宏观尺度下均质混凝土模型相同。A-I“键”和C-I“键”分别为骨料、砂浆与界面过渡区相连,因此假设它们的力学性能与I-I“键”相同。
不同的“键”类型确定后,需要进一步确定每种类型的“键”所占比例。作为尝试,本文采用一种简化方法,假设每种“键”的比例与各相的体积分数成线性关系,各相体积分数保持不变,则每种“键”的比例也将是固定的。例如,骨料的体积分数、砂浆的体积分数、界面过渡区的体积分数分别为a,b和c,三种“成分键”的比例分别为aa(A-A“键”)、bb(C-C“键”)、cc(I-I“键”),三种“界面键”的比例分别为是2ab(A-C“键”),2ac(A-I“键”),2bc(C-I“键”)。上文提到假定A-I“键”与C-I“键”的力学性能与I-I“键”相同,因此最终有四种类型的“键”,比例分别为aa,bb,cc+2ac+2bc,2ab。
亚均质模型中不同类型“键”的确定作为预处理过程实现,具体步骤如下:
(1) 对于每个物质点近场范围内所有完整的“键”,生成随机数m,m是一个0~1之间的任意实数;
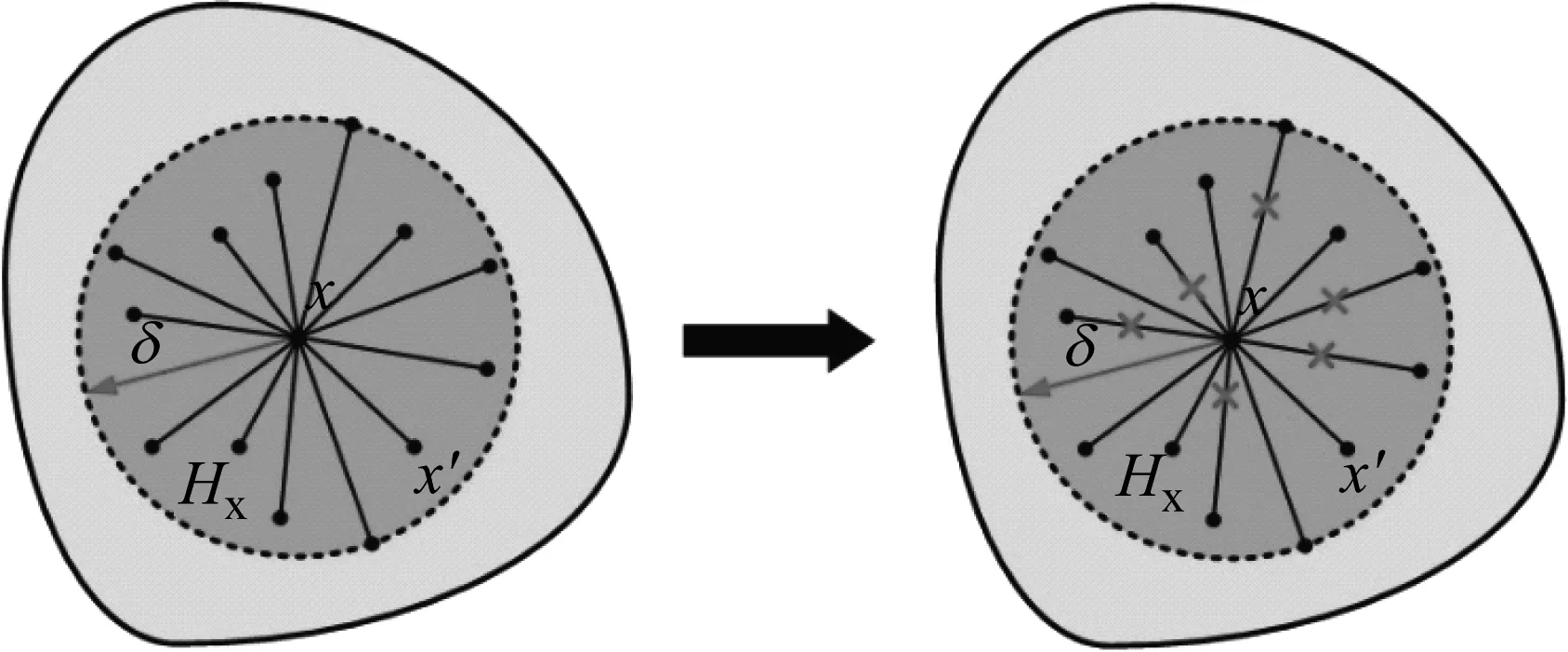
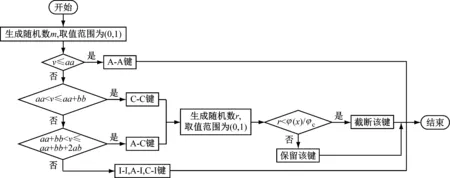
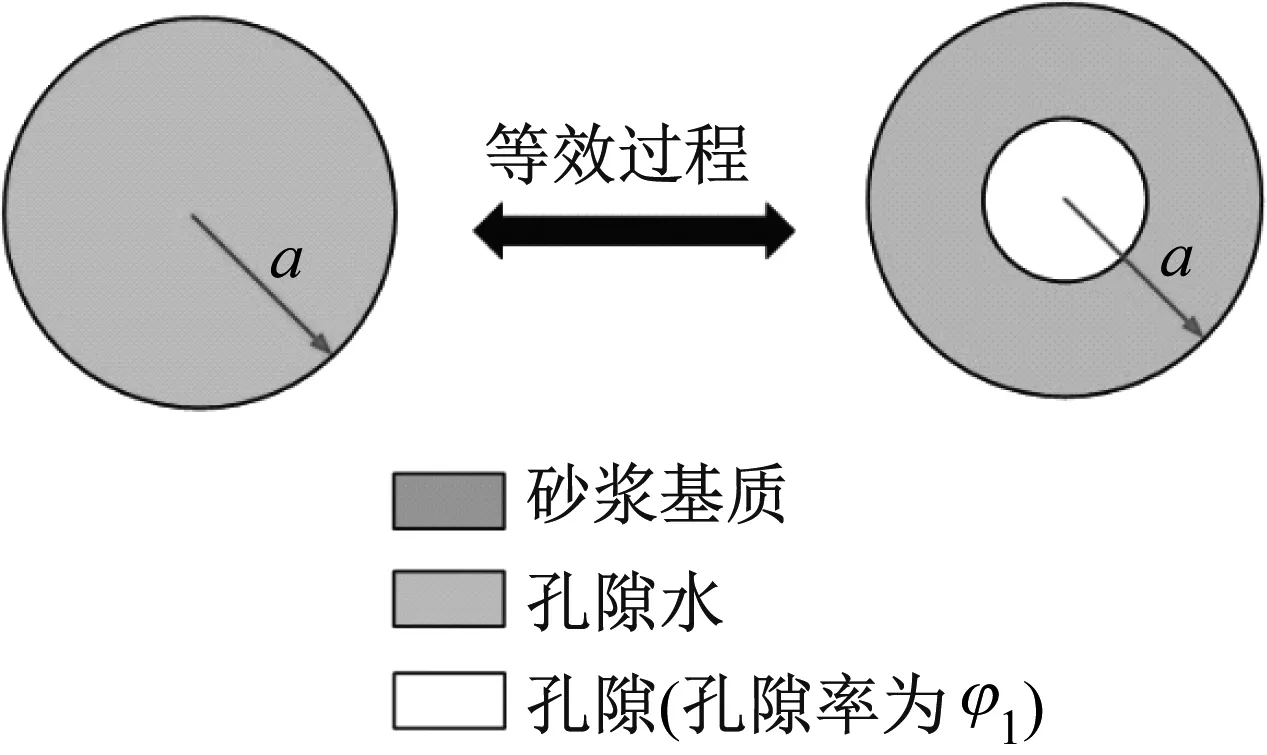
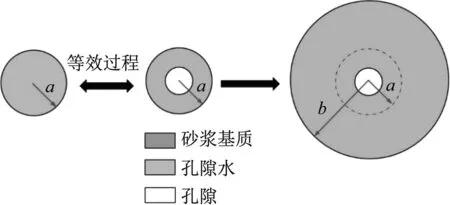
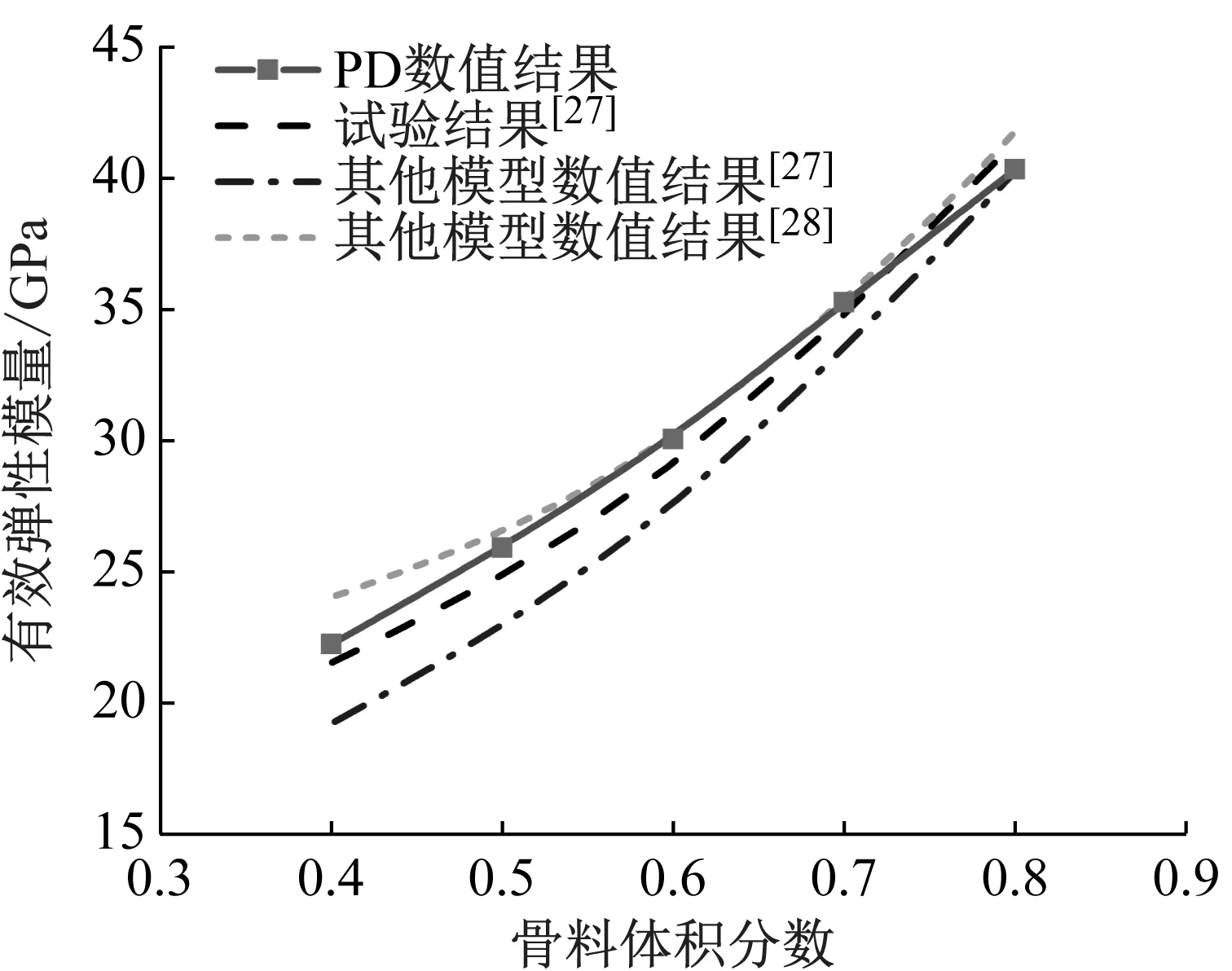
(2) 如果m≤aa,说明该“键”为A-A“键”;如果aa (3) 确定“键”的类型并赋予相应的力学参数后,转到下一个“键”继续判断。 混凝土砂浆中天然存在的孔隙结构表明该处存在缺陷,而近场动力学亚均质模型是作用在“键”层次上的,因此可以通过物质点对间“键”的缺失来表示内部孔隙的存在。与2.1节相同,先确定不同“键”的类型,再通过随机判断“键”是否截断。该过程无需删除孔隙范围的物质点,只需将穿过孔隙范围的“键”在预处理过程中预先截断即可。考虑孔隙的亚均质模型的核心思想为在均匀离散计算模型中通过预先截断一定比例的“键”来考虑初始损伤量,以此表示混凝土结构内部的孔隙,断“键”示意图如图3所示。 图3 近场动力学亚均质模型断“键”示意图Fig.3 Schematic of bond broken of IH-PD model 定义任意物质点其近场范围内预断“键”指数为d (11) 式中:φ(x)为给定的材料孔隙率;φc为临界孔隙率。当材料孔隙率达到临界孔隙度时,与该点相关的所有“键”都应被破坏。对于零孔隙率的材料,则不引入预断键(所有物质点的预断“键”指数均为零)。 具体的预断“键”步骤如下: (1) 对于每个物质点近场范围内所有的完整的“键”,生成随机数v,v是一个0~1之间的任意实数; (2) 如果v<φ(x)/φc,说明该“键”为预断“键”,并更新“键”两端物质点信息; (3) 转到下一个“键”继续判断。 根据上述步骤,在预断“键”过程中每个“键”(连接两个物质点)都要进行两次判断过程。假设两个物质点出孔隙率分别为φ(x)和φ(x′),则该“键”保持完整的概率为(1-φ(x)/φc)(1-φ(x′)/φc)。假设材料的孔隙率一致,均为φ,则每个“键”保持完整的概率为(1-φ/φc)2。在这种情况下,任意物质点处的预损伤指数即预断“键”数与“键”总数之比为 1-(1-φ/φc)2 (12) 本文中亚均质模型假设在骨料与界面过渡区中不考虑孔隙的存在,因此只需要考虑砂浆的孔隙率。结合上一节中确定不同“键”类型的预处理过程以及预断“键”过程,流程图如图4所示。假如骨料、砂浆以及界面过渡区的体积分数分别为a=40%,b=55%,c=5%,孔隙率φ=10%(φc=1.0),那么A-A“键”所占比例为16%,C-C“键”所占比例为30.25%,A-C“键”所占比例为44%,I-I“键”所占比例为9.75%,预断“键”所占比例为C-C“键”与A-C“键”的10%,每个“键”保持完整的概率为81%,预损伤指数为0.19。 图4 考虑孔隙的近场动力学亚均质模型预处理算法流程图Fig.4 The flowchart for the pre-processing algorithm in IH-PD model considering the pore 混凝土宏观力学性能会受到孔隙影响。本文借鉴文献[22]中的处理方法,将带孔隙的水泥砂浆看成是由砂浆基质(孔隙率为零)和孔隙组成的两相介质。这里假设孔隙率为水泥砂浆中所有孔隙所占的体积分数,并且孔隙率保持恒定不变。对如图5所示的含孔隙的水泥砂浆进行简化分析,简化为两相球模型(各向同性弹性空心球),含孔隙的水泥砂浆的有效体积模量与剪切模量分别为 (13) μ*=μm(1-φ2) (14) 图5 含孔隙的水泥砂浆示意图Fig.5 The schematic of cement mortar with pores 当混凝土长时间处于水环境中,在外部水压力下,混凝土内部孔隙完全充满水分,即认定混凝土为完全饱和状态。对于饱和混凝土,本节在含孔隙混凝土的亚均质模型基础上,进一步考虑孔隙内部水分对混凝土砂浆基质有效体积模量与剪切模量的影响。 饱和混凝土中水泥砂浆成分被看作为砂浆基质与自由水组成的两相复合材料,由于孔隙中完全充满水分,因此自由水的体积分数之和与孔隙率相等。简化的两相球模型为各向同性弹性空心球模型,其中内外球半径分别为a、b,孔隙率可以表示为φ=a3/b3。 由于孔隙中完全充满水分,为了建立自由水与孔隙之间的关系,可以对孔隙水进行力学等效分析。孔隙水体积模量为Kw,并且Kw (15) 根据式(15),可以得到孔隙水等效的孔隙率φ1为 (16) 为了得到饱和混凝土的有效体积模量,将混凝土中孔隙水代替为图6中孔隙水等效后的模型,形成图7中的等效球体,即饱和混凝土中水泥砂浆的有效体积模量与图7中等效球体中水泥砂浆的有效体积模量相等。 图6 孔隙与孔隙水球体的等效过程Fig.6 The equivalent process of pore and free water 图7 饱和混凝土整体等效过程Fig.7 Whole equivalent process of saturated concrete 中心球体孔隙率为φ1,可以得到等效球体的孔隙率为 (17) 将式(17)中孔隙率φ2代入到式(15)中,可以得到孔隙率为φ的饱和混凝土水泥砂浆的有效体积模量 (18) (19) 考虑三维混凝土板中的弹性波传播过程,通过在混凝土板边缘区域上突然施加一个脉冲力来产生弹性波,根据弹性波波速计算混凝土有效弹性模量,并与试验数据进行对比。混凝土板尺寸为1 m×1 m×0.05 m,如图8(a)所示。加载情况如图8(b)所示,在底部一侧区域(长度为100 mm)上突然施加1 MPa的竖向载荷,并保持5 μs不变,然后移除载荷,不再施加外力。在近场动力学模拟中,模型采用尺寸为Δx=0.01 m的均匀网格进行离散,近场范围为δ=0.04 m,近场范围为四倍物质点间距δ=4Δx,模型共有61 206个物质点。各相成分的材料参数见表1[25]。本文设定骨料体积分数为40%,水泥砂浆体积分数为55%,界面过渡区体积分数为5%,除另外规定外,本文算例均采用此比例标准。 (a) 混凝土板的几何模型 表1 混凝土各相成分的材料参数Tab.1 Material parameters of each phase of concrete 根据固体介质中的波传播理论[26],非均质材料波速Cw与有效弹性模量E′的关系为 (20) 图9分别为试验结果[27]、近场动力学模拟结果以及其他数值模型得到的混凝土有效弹性模量[28]。从图中可以看出,混凝土的有效弹性模量随着骨料体积分数的增大而逐渐增大,并且本文计算得到的有效弹性模量与其他数值模型结果以及试验数据吻合良好。值得注意的是,当骨料体积分数达到80%时,近场动力学亚均质模型的结果略小于试验结果。造成这种现象的原因可能是因为在近场动力学亚均质模型中没有考虑骨料的实际形状和大小,对实际计算结果造成一定的误差。 图9 混凝土有效弹性模量的试验结果与数值模拟结果比较Fig.9 Comparison between simulation results and experimental results for effective elasticity modulus 不同孔隙率下计算得到的应力波传播速度如图10(a)所示,孔隙率分别为0,10%,30%,50%,70%。可以看出,随着孔隙率的增加,波传播速度越来越慢,波速与孔隙率之间接近为线性关系。根据式(20)与不同孔隙率下的波速,可以计算得到不同孔隙率下混凝土有效弹性模量,如图10(b) 所示。由图可见,本文计算结果与试验数据[29]吻合良好,说明本文模型方法能够准确反映混凝土有效弹性模量与不同孔隙率之间的定量关系。 图11与图12分别为本文数值结果中不同孔隙率下饱和混凝土与干燥混凝土的有效弹性模量,并与相应的试验结果及其他数值模型数值结果对比。由图可见,无论混凝土处于饱和状态还是完全干燥状态,随着内部孔隙率的增加,混凝土有效弹性模量均呈现下降趋势。本文得到的混凝土有效弹性模量与试验结果吻合较好,说明本文模型方法对于研究饱和混凝土力学行为具有适用性。 (a) 应力波波速 图11 不同孔隙率下饱和混凝土有效弹性模量Fig.11 Effective elasticity modulus of saturated concrete at different porosity 通过对比图13完全饱和状态下与完全干燥状态下混凝土的有效弹性模量可以发现,相同孔隙率下,当混凝土内部充满水分后,其有效弹性模量要大于干燥混凝土有效弹性模量。这是由于饱和混凝土孔隙内部的自由水限制了孔隙周围基质的变形,导致混凝土刚度有所提高。此外,随着孔隙率的增加,两者有效弹性模量的差距越来越大。 图12 不同孔隙率下干燥混凝土有效弹性模量Fig.12 Effective elasticity modulus of dry concrete at different porosity 图13 饱和混凝土与干燥混凝土有效弹性模量比较Fig.13 The comparison of effective elasticity modulus of saturated concrete and dry concrete 本节应用所提出的模型对饱和混凝土板的冲击破坏过程进行分析。算例中的几何尺寸、边界条件与试验[30]保持一致,如图14所示。混凝土靶体浇筑在直径800 mm、厚度为300 mm的圆筒形钢型涵洞内。冲击弹丸视为刚性体,质量为2.44 kg,弹丸初始速度为333 m/s。混凝土抗压强度为42 MPa,混凝土内部孔隙率选择为6%。近场动力学模拟中,模型采用尺寸为Δx=7 mm的均匀网格进行离散,近场范围为δ=28 mm,近场范围为四倍物质点间距δ=4Δx,模型共有579 872个物质点。各相成分的材料参数见表2。 图14 混凝土靶板冲击破坏试验模型示意图Fig.14 Projectile perforation in concrete target 图15(a)显示了本文模型和方法得到的冲击物加速度-时间关系曲线以及相应的试验结果,图15(b)为冲击物速度-时间关系曲线的模拟结果与试验结果。通过对比可以发现,本文数值结果中加速度曲线在中间段略高于试验结果曲线,导致冲击物速度曲线在相应段内降低幅度大于试验结果曲线。同时,在2 ms时,本文数值结果得到的冲击物残余速度为82 m/s,与试验结果75 m/s吻合较好。综合来看,本文数值结果与试验结果得到的冲击物加速度与速度曲线具有较好的一致性。 表2 混凝土各相成分的材料参数Tab.2 Material parameters of each phase of concrete (a) 加速度曲线 试验结果和本文数值结果中混凝土靶板破坏形态如图16(a)所示,图16(b)为混凝土靶板截面图。由图16(a)可以看出,试验观测结果与本文数值计算结果吻合较好,冲击面发生明显的成坑破坏,但是并未出现宏观裂纹。值得注意的是,试验结果中冲击面破坏形态是非对称的,左上角区域破坏明显差异较大。试验结果中靶板冲击面成坑半径以及成坑深度为223.67 mm、84.91 mm,结痂半径以及结痂深度分别为375.26 mm、146.38 mm,本文数值模拟结果中冲击面成坑半径以及成坑深度为257.43 mm、58.33 mm,结痂半径以及结痂深度分别为370.49 mm、141.04 mm。可以看出,本文模型数值结果与试验观测结果吻合较好,适用于饱和混凝土的冲击破坏问题。 (a) 冲击面 图17为饱和混凝土靶板随时间变化的损伤演化过程。在开始阶段,当冲击物接触靶板时,贯穿过程进入成坑破坏阶段,冲击物顶端区域形成环型损伤区。产生的应力波沿冲击物顶端向靶板底部传播,并且底部由于压缩波作用而逐渐形成塞锥型的损伤区。随着冲击物进一步贯穿靶体,贯穿过程进入穿隧阶段。当贯穿过程进一步进入剥落破坏阶段时,损伤区在底部进一步发展并形成结痂破坏。最后,冲击物完全穿透靶板,部分喷出物和碎片从后表面冲出。 0.1 ms 图18显示了饱和混凝土与干燥混凝土贯穿过程中冲击物加速度-时间关系曲线以及冲击物残余速度-时间关系曲线。从图中可以看出,饱和混凝土与干燥混凝土冲击物加速度与残余速度曲线的变化趋势基本一致。但不同饱和度下冲击物加速度曲线存在差异,相应的不同饱和度下冲击物残余速度曲线在500 μs后也逐渐开始不同。最终,干燥混凝土下冲击物残余速度要大于饱和混凝土,充分说明在高应变率加载过程中,饱和混凝土与干燥混凝土相比下具有更高的承载能力。 (a) 加速度曲线 本文提出一种考虑孔隙作用的亚均质近场动力学饱和混凝土模型,应用于饱和混凝土的动态冲击破坏问题分析,主要结论如下: (1) 本文构建的近场动力学模型适用于饱和混凝土动态问题,对混凝土波传播过程以及冲击破坏试验进行数值模拟,结果表明该模型能够准确模拟饱和混凝土动态力学特性及冲击破坏过程。 (2) 随着内部孔隙率的增加,混凝土有效弹性模量均呈现下降趋势。在相同孔隙率下,当饱和混凝土内部充满水分后,孔隙内部的自由水限制了孔隙周围基质的变形,导致混凝土刚度有所提高,因此饱和混凝土的有效弹性模量要大于干燥混凝土有效弹性模量。随着孔隙率的增加,两者有效弹性模量的差距有明显增大趋势。 (3) 在高速冲击载荷下,干燥混凝土中冲击物残余速度要高于饱和混凝土,表明饱和混凝土的抗冲击强度及抗侵彻能力有所提高。这一研究结果表明,由于饱和混凝土具有更加敏感的应变率特性,在高应变率加载过程中,其承载能力反而大于干燥混凝土。2.2 考虑孔隙的混凝土亚均质近场动力学模型

2.3 饱和混凝土有效力学特性

3 数值算例
3.1 混凝土板中的弹性波传播





3.2 饱和混凝土冲击破坏






4 结 论

