综合大质量偏心与弹簧横向刚度超静主动隔振平台动力学解耦控制研究

杨鸿杰，代 锋，刘 磊，李新国

(1.西北工业大学 航天学院，西安 710072；2.陕西省空天飞行器设计重点实验室，西安 710072;3.中国空间技术研究院西安分院，西安 710000)

高精密仪器设备如空间光钟、空间望远镜等对微振动环境的要求愈发苛刻[1-4]。微振动的特点在于振动幅值小，一般在mg量级，但振动频率范围宽[5-6]。从传递路径上区分，微振动隔离方式可分为扰源处隔离、传递路径隔离以及有效载荷处隔离[7-8]。针对扰源和有效载荷的微振动隔振手段有正、负刚度并联的低频隔振器[9]，磁悬浮式多自由度主动隔振器[10]，将星上扰源和超静载荷从物理上隔离的分离式隔振平台等[11-12]。六支腿或八支腿并联式主动隔振平台由于其宽频带振动隔离性能，在航空航天领域里得到了广泛应用[13-14]。在工程应用中，隔振载荷的质量偏心和连接弹簧的横向刚度诱发多自由度动力学耦合问题不仅增加主动隔振平台支腿弹簧刚度、支腿安装构型的设计难度，而且降低主动隔振性能。

动力学耦合导致主动隔振平台从基座扰动输入到隔振平台加速度输出的传递曲线存在多个耦合谐振频率[15]，在控制上是一个多输入多输出系统。一方面多输入多输出系统控制器设计较为困难，另一方面控制器在执行过程中消耗较多的计算资源，不利于高带宽隔振控制器的实时运行。通过优化支腿安装构型可设计出多自由度解耦或弱耦合的主动隔振平台，例如弱耦合的六作动器Cubic构型[16-17]，完全解耦的八作动器各向同性构型等。在隔振平台构型优化过程中采用的动力学模型多面向控制需求所建立，建模中忽略了弹簧或柔性铰链横向刚度以降低支腿安装雅克比矩阵的维数[18-19]。采用忽略横向刚度的动力学模型进行隔振平台构型优化，可能会导致优化构型不能实现动力学解耦。此外构型优化中需假设载荷质心是隔振平台的形心，或保持固定高度不变，因此当隔振载荷质心高度变化时，隔振平台动力学解耦可能会失效。部分文献考虑了弹簧横向刚度的影响，但尚未深入探讨横向刚度对隔振平台动力学耦合特性的影响[20]。

为克服构型优化实现动力学解耦方法的不足，从控制方法实现隔振平台动力学解耦得到广泛关注。美国空军实验室开发的VISS主动隔振平台隔振控制器忽略多支腿之间的动力学耦合，每个支腿被视为独立的控制通道，从而将隔振平台从多输入多输出系统简化为六个单输入单输出系统[21]。但由于多支腿之间控制带宽不同，导致主动控制力可能经过耦合通道传递到隔振载荷。并且若某个支腿因故障失效后，可能会导致隔振载荷多个自由度隔振性能的下降。张培军等[22]基于filtered-x least mean square (FXLMS)算法将隔振平台耦合通道划分为子通道和次级通道实现解耦控制，开展了定频扰动的解耦隔振实验，但基于FXLMS的解耦控制方法对于变频扰动的隔离性能有待研究。王晓雷等[23]利用模态向量的正交性对主动隔振平台动力学模型中质量矩阵和刚度矩阵进行对角化，在模态空间中实现解耦隔振控制，但动力学模型中尚未考虑连接支腿横向刚度的影响，导致模态矩阵计算不准确。于帅彪等[24]利用实验辨识模态坐标下面向控制的隔振平台动力学模型，但辨识的参数在模态坐标系下，不便用于隔振平台弹簧刚度和安装构型的优化设计。

本文首先综合载荷大质量偏心和弹簧横向刚度建立超静主动隔振平台耦合动力学模型，分析其动力学耦合特性，为隔振平台参数设计和动力学解耦隔振控制提供精确的模型参考。随后给出模态空间动力学解耦隔振控制策略。最后通过实验验证所建立动力学模型的准确性和解耦隔振控制方法的有效性。

1 超静主动隔振平台耦合动力学建模

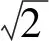
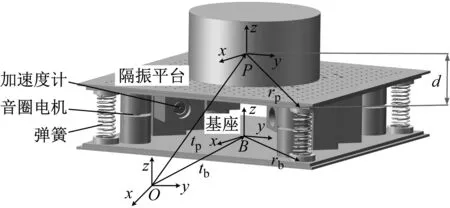
图1 主动隔振平台三维模型和坐标系Fig.1 Three-dimensional model and coordinate system of active vibration isolation platform

为了描述隔振平台的运动，建立与地面固连的惯性坐标系Oxyz，与基座质心固连的坐标系Bxyz以及与隔振平台质心固连的坐标系Pxyz。tp和tb分别是隔振平台坐标系原点和基座坐标系原点在惯性坐标系下的位置，d是隔振载荷质心与弹簧连接点的偏心高度。隔振平台的牛顿-欧拉动力学方程可写成

(1)

式中：Mp和Ip分别是隔振平台的质量和转动惯量；ωp是隔振平台的转动角速度；Fd和Td是施加到隔振平台的扰动力和力矩；Fc和Tc是主动控制力和力矩。

施加到隔振平台的扰动力和力矩主要因弹簧变形产生，单根弹簧除了轴向扰动力外，还需考虑沿横向的扰动力，如图2所示。

图2 弹簧的横向力和轴向力Fig.2 Transverse forces and axial forces of spring

第i根弹簧施加到隔振平台的扰动力可写成

(2)

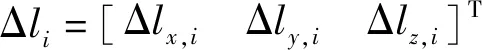
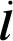
(3)

(4)

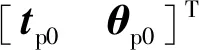
弹簧的安装雅克比矩阵Jp和Jb可表示为

(5)

式中：rpi和rbi分别是弹簧在隔振平台和基座坐标系下的安装位置；τpi和τbi分别是弹簧在隔振平台和基座的安装方向向量。

考虑弹簧横向刚度下，单个弹簧存在三个方向向量，与弹簧弹力方向一致。弹簧安装方向向量示意图如图3所示。在隔振平台构型设计确定的情况下，弹簧安装在隔振平台上的位置pti可以确定，因此弹簧在隔振平台坐标系下的安装位置与载荷质心偏心高度d有关。

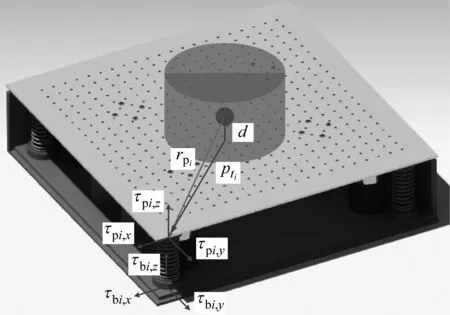
图3 弹簧安装方向向量示意图Fig.3 Schematic of spring installation direction vector

联立式(2)、式(3)、式(4)和式(5)，弹簧施加到隔振平台的作用力可写成

(6)

其中：K=diag([kx,1ky,1kz,1…kx,8ky,8kz,8]T),

C=diag([cx,1cy,1cz,1…cx,8cy,8cz,8]T)。

式(6)中弹簧扰动力Fs，l施加在弹簧与隔振平台的安装位置处，需要投影成相对于隔振平台质心的力和力矩

(7)

将式(6)和式(7)代入式(1)可得超静主动隔振平台的耦合动力学方程

(8)

2 超静主动隔振平台动力学耦合特性分析

动力学耦合导致基座某一自由度上的扰动传递到隔振平台的多个自由度。本章综合耦合通道的影响对隔振平台动力学耦合特性进行分析，为连接弹簧刚度设计、安装构型设计以及隔振控制器设计提供模型参考。

隔振平台弹簧编号和安装尺寸如图4所示。

图4 弹簧编号和安装示意图Fig.4 Number and installation location of spring

图4中1～4号为垂直安装弹簧，5～8号为水平安装弹簧。微振动环境下，弹簧安装方向向量τbi和τpi大小和方向近似相等，统一用τi表示，可写成

(9)

(10)

根据图4所示的安装构型，弹簧的安装方向向量如表1所示。

表1 1～8号弹簧的安装方向向量Tab.1 Installation direction vectors of No.1-No.8 spring

以y方向线运动和绕x轴转动说明隔振平台动力学耦合的原因。如图5所示，当隔振平台沿y方向运动时，弹簧产生阻碍隔振平台运动的力fk。由于弹簧力不过隔振平台的质心，因此会产生绕x轴的力矩mx，导致隔振平台y方向线运动和绕x轴转动运动耦合。

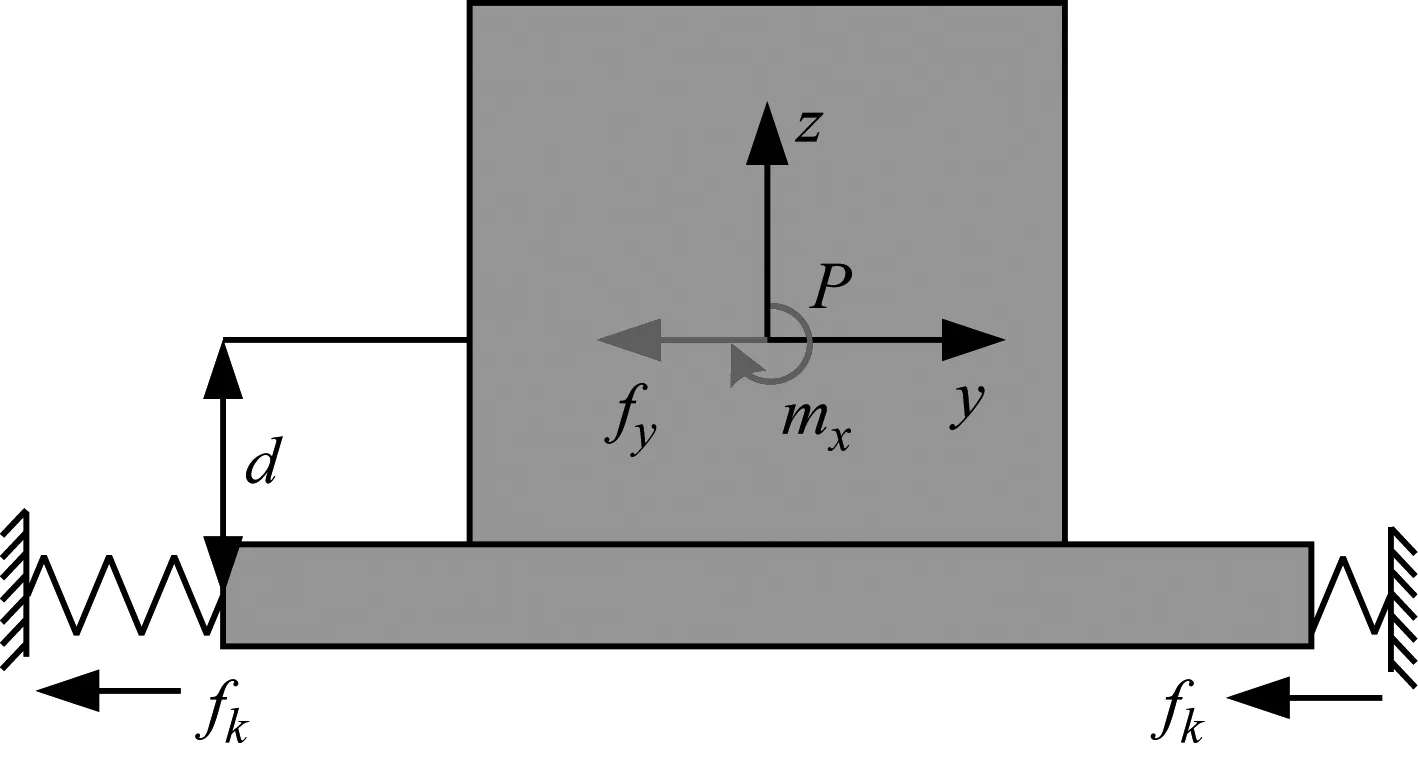
图5 y方向线运动和绕x轴转动耦合分析Fig.5 Coupling analysis of linear motion in the y direction and rotation about the x axis

根据隔振平台动力学模型式(8)，y方向线运动和绕x轴转动的耦合动力学方程为

(11)

其中:c22=4cvy+2chy+2chz，

k22=4kvy+2khy+2khz，

c24=c42=-4cvyd-2chyd-2chzd,

k24=k42=-4kvyd-2khyd-2khzd,

式中：kvx、kvy、kvz代表垂直安装1～4号弹簧的刚度；cvx、cvy、cvz代表垂直安装1～4号弹簧的等效阻尼；khx、khy、khz代表水平安装5～8号弹簧的刚度；chx、chy、chz代表水平安装5～8号弹簧的等效阻尼。

由式(11)中可看出，刚度矩阵和阻尼矩阵中非对角线元素值与载荷偏心高度d和弹簧横向刚度相关。根据式(11)得到从基座y方向加速度扰动输入到隔振平台y方向加速度的输出传递函数为

Gyy=

(12)

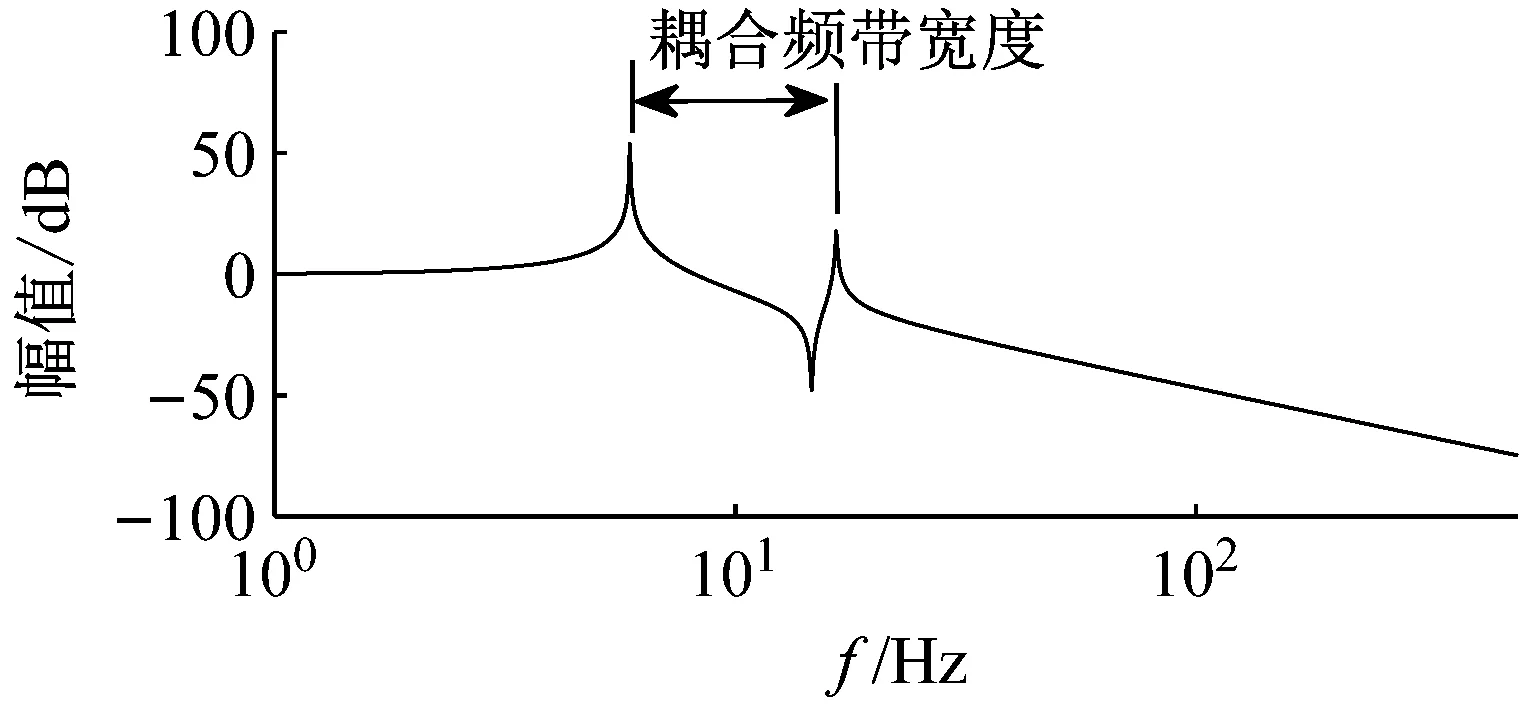
式(12)表明，从y方向基座扰动到隔振平台y方向输出的扰动传递函数Gyy是四阶系统。仿真中隔振平台和弹簧的参数如表2所示。根据式(12)绘制扰动传递函数Gyy的伯德图如图6所示。

表2 隔振平台和弹簧仿真参数Tab.2 Parameters of isolation platform and spring

(a)

由图6可看出，由于y方向线运动和绕x轴转动的耦合，从y方向基座扰动到隔振平台y方向输出的扰动传递曲线有两个谐振峰，谐振频率分别是5.9 Hz和16.6 Hz，对应扰动传递函数Gyy的两个极点。两个谐振峰之间14.6 Hz处局部最小值对应扰动传递函数Gyy的一个零点。扰动传递函数Gyy两个极点可通过求解式(11)对应的自由振动的特征方程为

(13)

求解式(13)可得扰动传递函数Gyy两个极点对应的频率分别是

(14)

式(14)表明,在隔振器被动隔振弹簧参数设计中，如果忽略弹簧的横向刚度，会导致隔振平台谐振频率实际值与设计值不符合，更严重导致隔振平台实际的动力学模型阶数与理论模型不符合，降低主动隔振控制性能。定义两个谐振峰之间的距离为耦合频带宽度，在弹簧刚度阻尼以及隔振平台质量特性不变时，扰动传递函数Gyy和耦合频带宽度随载荷偏心高度d的变化,如图7所示。

由图7可知，当隔振载荷质心高度d降低时，第二个谐振峰ω2对应的增益降低，表明动力学耦合效应减弱。当质心高度d为零时，y方向线运动和绕x轴转动角运动解耦，此时传递函数Gyy的阶数降为2阶。

3 超静主动隔振平台解耦控制方法

隔振平台多自由度动力学耦合导致控制器设计较为复杂，实时控制过程消耗较多的计算资源，不利于高带宽隔振控制器的实时运行。从安装构型上实现隔振平台的动力学解耦存在隔振载荷质心高度变化导致解耦失效的缺点。本章从控制方法对超静主动隔振平台动力学解耦进行研究，给出了基于模态空间解耦的隔振控制方法，并对该方法的有效性进行了实验验证。

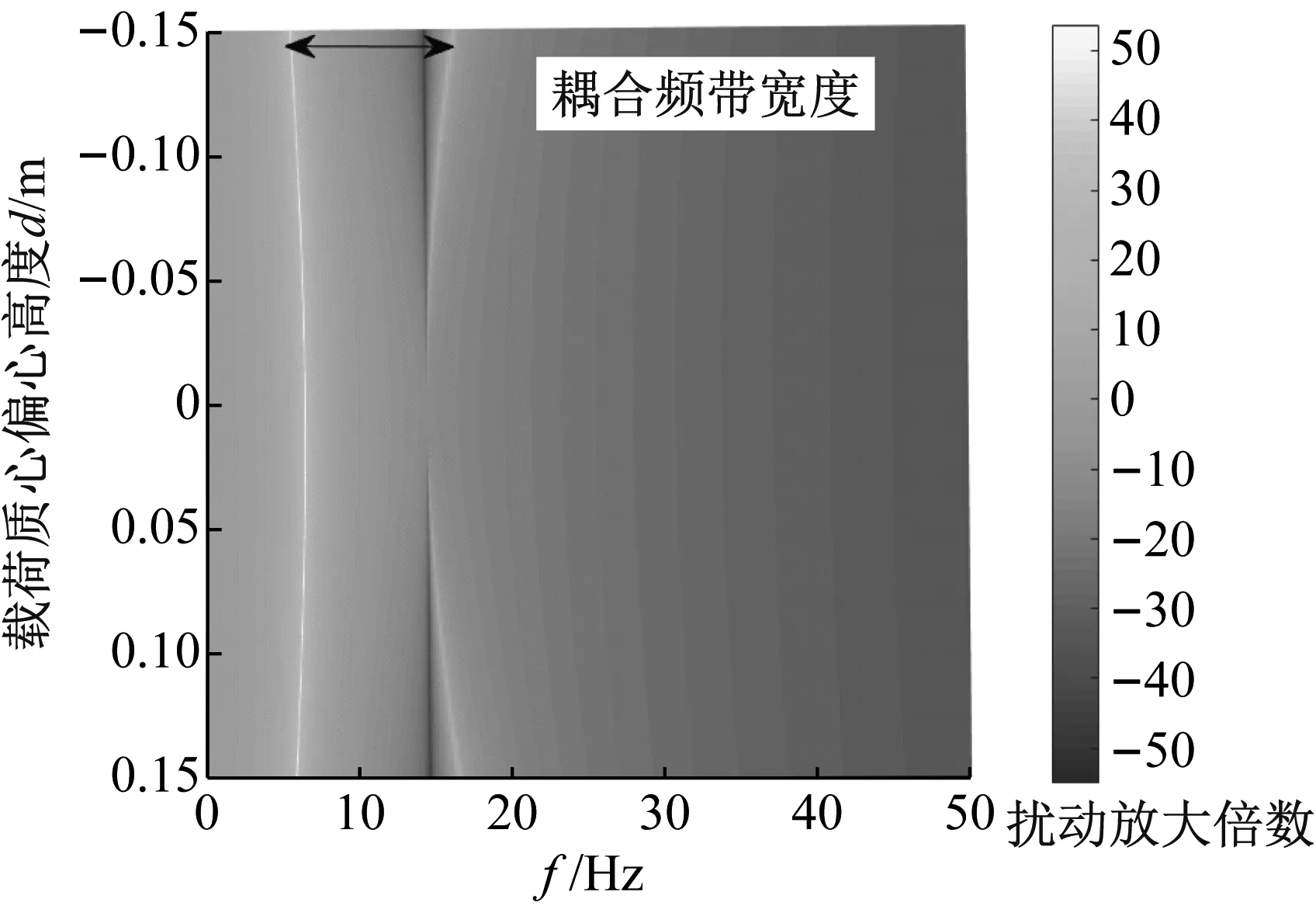
图7 耦合频带宽度随载荷质心高度d的变化Fig.7 Coupling bandwidth changes with height of mass center

通过模态矩阵对隔振平台y方向加速度和绕x轴角加速度进行如下变换

(15)

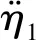
将模态矩阵代入到式(11)得

(16)

式(16)左右两边同时左乘ΦT

(17)

根据式(17)可在模态坐标下设计解耦隔振控制器。为验证隔振平台的动力学耦合特性和解耦隔振控制方法，开发了主动隔振实验平台如图8所示。

主动隔振平台不安装水平弹簧，仅通过四根弹簧垂直弹簧支撑，以验证垂直弹簧横向刚度的影响。隔振平台上安装有模拟载荷，两个音圈电机和三个加速度传感器，音圈电机安装方向向量与z轴平行，1号和2号加速度传感器分别与两个音圈电机同轴安装。3号加速度传感器安装在侧面，安装方向与y轴平行。

图8 主动隔振实验平台示意图Fig.8 Diagram of vibration isolation platform

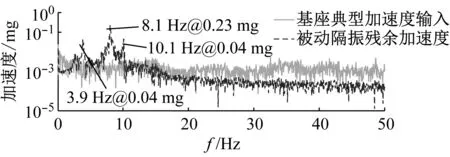
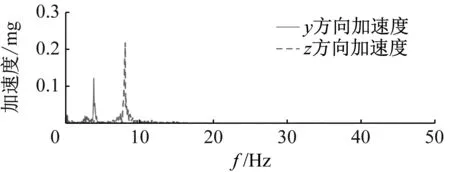
在实验室楼面自然微振动扰动输入下，被动隔振时1号加速度传感器测量值时域和频域如图9所示。由图9可知，1号加速度传感器频域加速度有3个谐振频率，从小到大分别对应隔振平台y方向，z方向和绕x轴转动的基频。

(a)

利用加速度传感器的安装雅克比矩阵将1号、2号和3号加速度传感器测量值变换成隔振平台y方向，z方向和绕x轴转动的加速度，如图10和图11所示。隔振平台动力学模型表明z方向动力学解耦，扰动传递函数的阶数是2，图10中隔振平台z方向加速度频谱曲线仅有一个峰值，与2阶系统传递函数特性吻合，表明理论动力学模型特性与实验系统相符合。

(a)

(a)

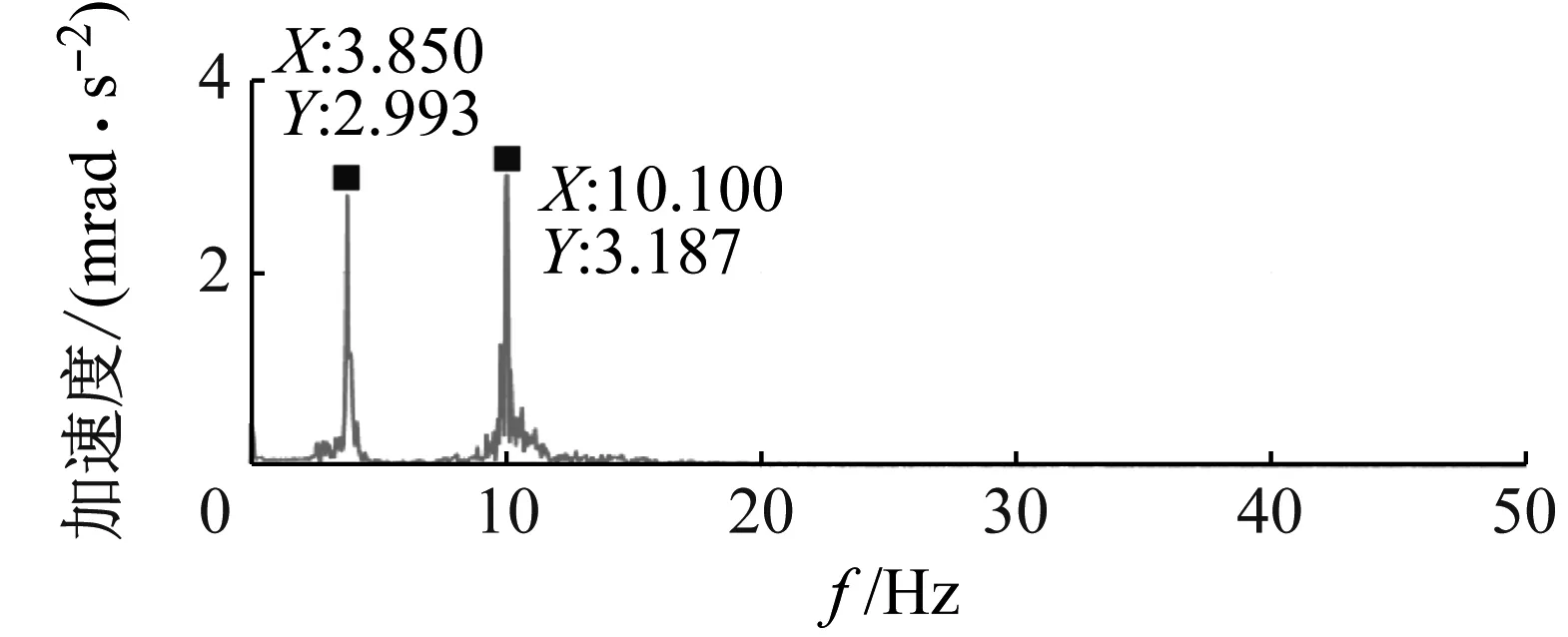
动力学耦合下隔振平台y方向加速度和绕x轴角加速度具有两个耦合谐振频率，实际测量出两个谐振频率分别是3.9 Hz和10.1 Hz，表明虽然隔振平台没有安装水平弹簧，但是由于垂直弹簧的横向刚度的作用，隔振平台y方向运动和绕x轴转动依然是耦合的，验证了所建立模型的正确性。

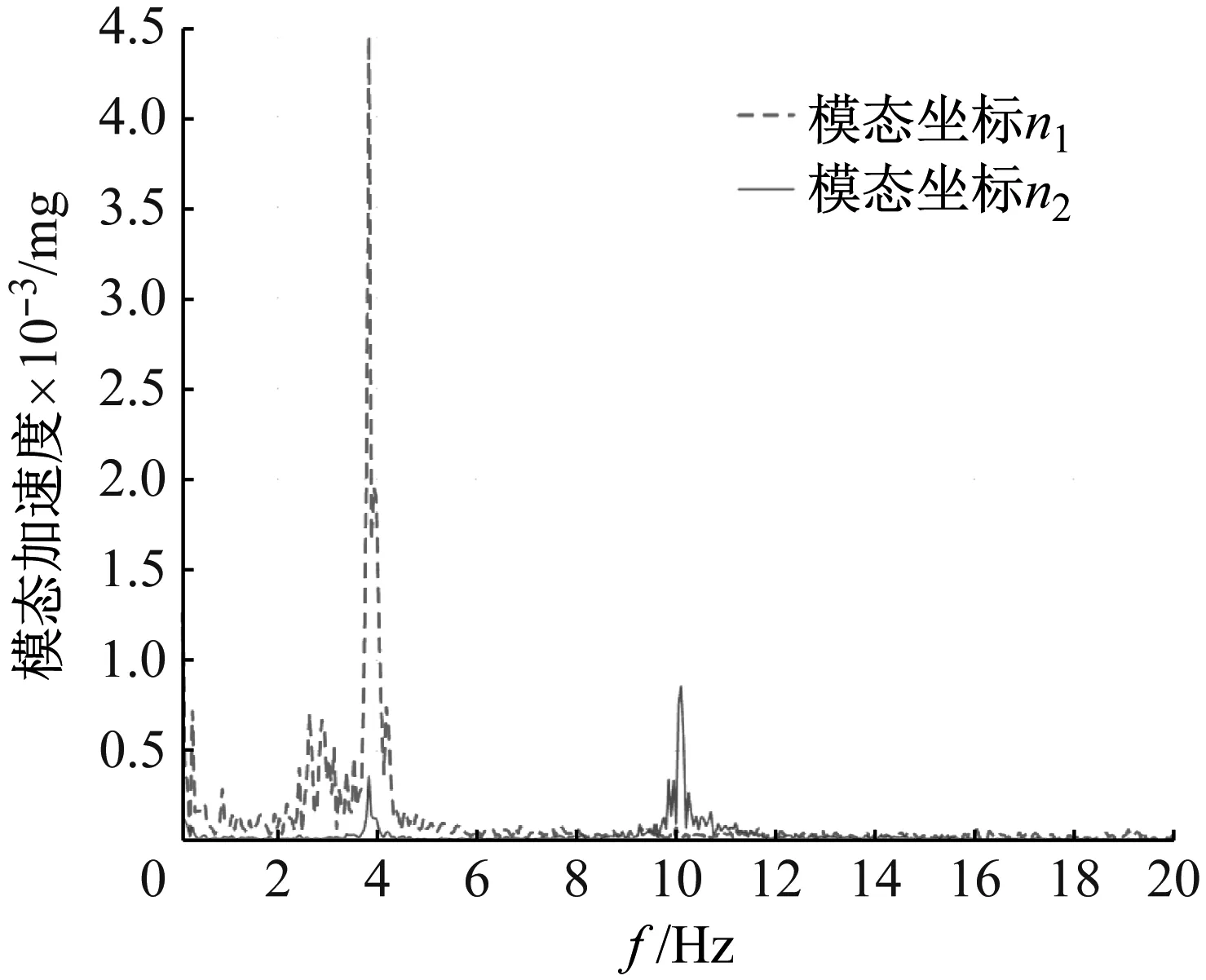
图12 模态坐标η1和η2加速度频谱图Fig.12 Spectrum of modal acceleration

基于模态空间的隔振平台动力学解耦控制方块图,如图13所示。

图13 解耦隔振控制策略Fig.13 Decoupling vibration control strategy

解耦隔振控制实施流程为：

(1) 根据式(4)，三个加速度传感器的测量值通过雅克比矩阵解计算得到隔振平台y方向，z方向和绕x轴转动的加速度；

(4) 根据式(17)，模态坐标系下PI隔振控制器的控制力通过矩阵(ΦT)-1变换得到相对隔振平台质心的控制力和力矩，最后通过控制力分配矩阵分配到两个音圈电机上，从而实现对基座扰动的振动隔离。

当隔振载荷质心高度发生变化时，通过模型辨识方法对隔振平台模态矩阵进行辨识，无需改变隔振平台弹簧安装构型可实现动力学解耦控制。

为了验证解耦隔振控制方法的有效性，分别开展两组解耦隔振控制实验。解耦隔振控制实验系统如图14所示。

加速度传感器(PCB 393B05)的测量值经过信号调理器调制和放大后以模拟电压信号输出，主控计算机利用16位模拟采集卡(NI 9205)对信号调理器输出的模拟电压信号进行采集，通过LabVIEW程序实现模拟电压信号到隔振平台加速度信号变换，隔振平台加速度信号到模态空间加速度变换，模态空间比例积分计算，最后通过16位模拟输出卡(NI 9264)输出控制电压给音圈驱动器。音圈驱动器根据转换系数将模拟输出卡的控制电压转换成参考控制电流，并通过内部电流环实现音圈电机线圈电流对参考电流的快速精确控制。

图14 解耦隔振控制实验系统组成Fig.14 Composition of decoupling vibration isolation control experimental

为满足隔振平台1 Hz左右低频微弱加速度信号测量和mg量级微振动主动控制需求，实验室自主研制了信号调理器、音圈电机和音圈电机驱动器等关键实验设备。实验设备的型号和参数如表3所示。

表3 实验设备型号和参数Tab.3 Model and parameters of experimental equipment

实验一：η2通道隔振控制开启，z方向和η1通道隔振控制关闭

从图15可看出，主动隔振前后模态坐标η2频谱中10.1 Hz频率对应的幅值从2.1×10-1下降到6.9×10-4，下降-50 dB。隔振前后1号加速度传感器时域和频域如图16所示。

(a)

(a)

由图16可知，仅对模态η2进行主动控制，1号加速度传感器时域加速度均方根下降6.37%。频域加速度10.1 Hz频率对应的幅值从8.5×10-2mg下降到4.1×10-3mg，下降26 dB。除模态η2通道对应10.1 Hz附近的振动得到衰减，1号加速度传感器频域加速度其余频率上不引入额外的振动，验证解耦隔振控制的有效性。

实验二：z方向和η2通道隔振控制开启，η1通道隔振控制关闭。

z方向和模态η2通道隔振控制开启前后，1号加速度传感器的时域和频域如图17所示。

(a)

相比于隔振前，主动隔振后1号加速度传感器时域加速度均方根下降77.22%。频域加速度8.1 Hz和10.1 Hz频率对应的加速度幅值分别从2.6×10-1mg和5.2×10-2mg下降到3.9×10-4mg和4.0×10-4mg，分别下降56 dB和42 dB。主动隔振后5～200 Hz频率范围内频域加速度最大幅值为1.8×10-2mg。

从实验结果可看出，解耦隔振控制策略可对单个解耦通道进行振动控制，验证了解耦隔振控制策略的有效性。在模态解耦坐标下，隔振控制对象简化成单输入单输出的2阶系统，有效降低了控制器设计的难度，提高了隔振控制器的实时执行效率。

4 结 论

本文研究超静主动隔振平台的耦合动力学建模和解耦隔振控制算法。仿真结果表明，隔振平台动力学建模、参数设计、以及主动隔振控制器需要合理综合载荷质量偏心和弹簧横向刚度导致的动力学耦合效应。隔振平台多自由度之间动力学耦合的原因在于弹簧力的方向不过隔振载荷的质心，导致弹簧力投影到隔振平台质心时产生了耦合力矩。解耦隔振控制可实现单个解耦通道的振动控制而不在其余通道引入额外振动。