基于裂纹扩展的锈蚀拉索疲劳寿命评估

王天鹏 ，张建仁 ，王磊 ，马亚飞

（1.长沙理工大学 土木工程学院，湖南 长沙 410114；2.中南林业科技大学 土木工程学院，湖南 长沙 410004）

腐蚀与疲劳是影响桥梁拉吊索耐久性的两个重要因素.已有研究成果表明［1-3］，高强钢丝是一种腐蚀敏感材料，腐蚀将导致钢丝的疲劳性能大幅下降，因此锈蚀拉索的疲劳寿命备受关注.

桥梁拉索是一个高冗余度构件，其系统失效由每一根钢丝逐步失效引起.纤维束强度理论模型的建立，为平行钢丝索的疲劳分析提供了理论基础.Stallings 和Frank［4-5］根据钢丝疲劳寿命的概率分布，基于线性累积损伤准则推导了整根斜拉索内任意一个钢丝断裂经历的疲劳循环次数，钢丝疲劳寿命概率分布假定了三种情况：对数正态分布、两参数及三参数Weibull 分布，为斜拉索疲劳寿命的数值模拟提供了研究思路.Castillo 等［6］推导了并联体系在常幅荷载作用下各并联单元的损伤累积过程，建立了考虑荷载重分布的并联体系内各并联单元疲劳寿命理论模型，但模型较为复杂，应用颇为不便.兰成明等［7］推导了表征平行钢丝斜拉索疲劳寿命的多参数Weibull 模型，根据疲劳截尾数据的条件概率分布建立疲劳模型参数EM估计算法，从线性累积损伤和钢丝P-S-N曲线等效损伤路径两个角度推导斜拉索内任意一根钢丝疲劳破坏所经历的循环次数，基于次序统计提出斜拉索疲劳寿命界限估计方法.研究表明斜拉索疲劳寿命由其小部分疲劳寿命较小的钢丝控制，以10%断丝率作为斜拉索疲劳寿命终止条件较合理；斜拉索疲劳寿命均值与其内钢丝数无关，钢丝数增加会减小斜拉索疲劳寿命的变异性，钢丝疲劳寿命的变异性对斜拉索疲劳寿命影响较大.

由上述成果可知，基于疲劳寿命曲线的拉索累积损伤评估方法概念清晰，被广泛采用，但未建立拉索腐蚀程度与疲劳寿命劣化之间的关系模型.随着断裂力学理论的发展，基于钢丝裂纹扩展的疲劳寿命计算方法逐渐被工程界所接受，并进行了一系列的试验与应用研究［8-10］.基于裂纹扩展的疲劳寿命计算方法考虑了荷载作用次序的影响，更方便利用钢丝的既有状态信息.但目前线弹性断裂力学方法多用于对锈蚀钢丝的疲劳分析，如何对拉吊索的疲劳寿命进行科学有效的评估仍需进一步研究.

本文在前期对钢丝裂纹扩展速率研究成果的基础上，基于纤维束模型，采用概率断裂力学理论对平行钢丝索疲劳寿命分布进行分析.建立随机荷载作用下拉索腐蚀程度与疲劳寿命劣化之间的关系模型，为在役拉索的安全评定提供科学依据.

1 钢丝疲劳裂纹扩展速率模型

1.1 模型参数计算

在早期的研究中，Smith 等［11］提出了可描述在近门槛值低速区和中部稳态扩展区的疲劳裂纹扩展速率表达式：

式中：a为裂纹尺寸；N为疲劳荷载循环次数；ΔK为应力强度因子范围；ΔKth为裂纹扩展门槛值；B、m分别为裂纹扩展系数和指数，其中m可近似取为2.0.文献［12］在此基础上给出了适用于缆索钢丝的模型参数计算方法：

式中：Δσ为应力范围；Y为裂纹形状因子，可根据裂纹尺寸a和钢丝直径计算［13］；ΔKth0为应力比R=0 时的裂纹扩展门槛值，可根据钢丝的屈服强度、脉动疲劳极限进行估算；σff为临界断裂应力；E为钢丝的弹性模量.

当钢丝的初始裂纹尺寸a0和临界裂纹尺寸ac已知时，应用式（1）～（4）计算钢丝的疲劳寿命与试验结果符合较好［12］.其中ac可由钢丝断裂韧度KC计算：

式中：σmax为最大循环应力.

1.2 钢丝的最大点蚀深度

根据已有试验研究成果，冷拔钢丝具有抗裂纹萌生能力强、抗裂纹扩展能力弱的特性，当钢丝发生腐蚀后，点蚀效应是形成疲劳源的主因［10］.这里近似认为腐蚀钢丝的初始裂纹尺寸a0为最大点蚀深度，通过a0的取值反映不同腐蚀程度钢丝的疲劳寿命.

钢材的点蚀深度与均匀腐蚀深度有关，通常用最大点蚀深度与均匀深度的比值来表征：

式中：Rp为点蚀不均匀系数；dmax为最大点蚀深度；dc为均匀腐蚀深度.

根据国内外学者对钢丝点蚀效应的研究成果，Rp是服从极值I型分布的随机变量，其在单位面积A0内的累积分布函数为［14］：

式中：A0=l0πD0，l0为钢丝单位长度，D0为钢丝的单位直径；μ0和α0为分布参数.假设钢丝各长度范围内的腐蚀行为是独立的，则对于任意面积A内Rp的累积分布函数为：

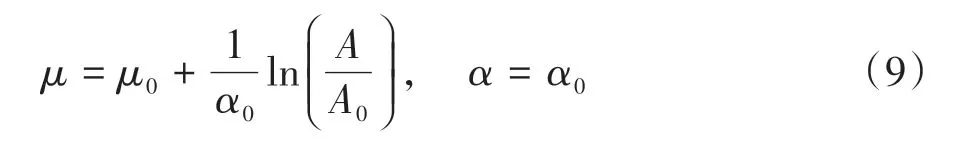
当钢丝直径一致时，A/A0=l/l0，l为钢丝长度.

2 拉索疲劳失效模拟方法

2.1 纤维束模型

对于平行钢丝索，当忽略钢丝间的接触摩擦力时，依据纤维束理论可将其视为由若干基本单元组成的串-并联模型［15］.其中单根钢丝相当于一个串联体系，整个拉索相当于多根钢丝组成的并联体系，拉索的纤维束模型如图1 所示.其中单根钢丝由n0个长度为L0的基本单元串联而成，整个拉索由n根长度为L的钢丝并联而成.

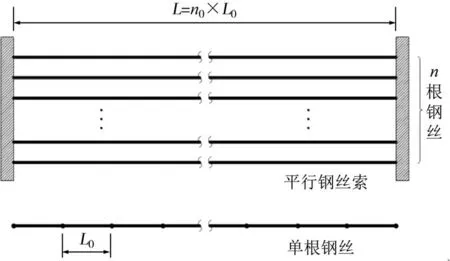
图1 拉索的纤维束模型Fig.1 Fiber bundle model of cable

根据串联模型中的“最弱联假定”，图1 中长度为L的钢丝疲劳寿命计算式为：

式中：Nw为钢丝的疲劳寿命；Ni（i=1，2，…，n0）是计算长度为L0的各基本单元的疲劳寿命.

2.2 疲劳失效全过程模拟方法

由于拉索断丝后的内力重分布效应以及疲劳损伤的累积效应，通过钢丝基本单元的疲劳寿命分布只能计算出第1 根钢丝断丝时的疲劳寿命［16］.为得到不同断丝率下拉索的疲劳寿命，采用全过程疲劳失效模拟法进行分析.疲劳失效全过程模拟方法将拉索视为一个多裂纹竞争的串-并联模型，对于每个基本单元进行全过程仿真失效模拟，具体步骤如下：

①根据给定的单元随机变量（如a0、ΔKth、B和KC等）概率分布模型随机生成一组n0×n的纤维束模型计算参数，通过迭代计算每个单元的累积裂纹尺寸和疲劳寿命：

式中：Δai为单元第i次更新时的裂纹扩展量；ΔKi为单元第i次更新时的应力强度因子幅值，f（ΔKi）为与之对应的裂纹扩展速率；ΔN为给定寿命计算步长.

②在每一次计算步完成后，对单元的裂纹长度进行判定.当某个单元裂纹长度超过临界尺寸ac判定为失效后，记录此时的疲劳寿命，将单元所在的串联体在矩阵中剔除，然后调整剩余钢丝的内力值并更新剩余单元的临界裂纹尺寸.

③采用更新后的钢丝内力值和临界裂纹尺寸继续采用逐次累加法计算剩余单元的累积裂纹长度，重复步骤②，直到拉索达到临界断丝数，则单次模拟结束.

④重复①②③，直至达到指定的试验次数，Monte-Carlo模拟结束.

以钢丝的最大点蚀深度作为初始裂纹尺寸，采用全过程失效模拟方法计算锈蚀拉索疲劳寿命的流程如图2所示.

图2 拉索疲劳寿命计算流程图Fig.2 Flow chart of cable fatigue life calculation

3 锈蚀拉索的疲劳寿命预测

3.1 试验信息

文献［17］采用一批服役18 年的斜拉索锈蚀钢丝组成拉索进行了疲劳试验，钢丝的初始公称直径为5 mm，强度级别为1 570 MPa.试验前选取腐蚀较严重的钢丝和未腐蚀钢丝进行拉伸试验，试验结果如表1 所示.试验结果显示，腐蚀钢丝与未腐蚀钢丝的弹性模量基本相同，可认为没有发生变化.腐蚀钢丝的名义屈服强度和名义极限强度降低约4%，然而钢丝均匀腐蚀截面损失率均值约4%，可以看出强度减小主要由于截面损失引起.

表1 钢丝拉伸试验结果Tab.1 Tensile test results of steel wire

试验索由69 根锈蚀钢丝组成，总长度为1 750 mm，无夹持自由段长度为1 190 mm，锚头按照实际拉索锚头构造制作的冷铸镦头锚，在大吨位疲劳试验机上对试验索进行了疲劳试验.试验时的初始应力幅Δσ=360 MPa，应力比R=0.5，试验过程中采用压电陶瓷传感器监测了两组试验索前7 根钢丝断裂时的疲劳寿命，试验结果如表2所示.

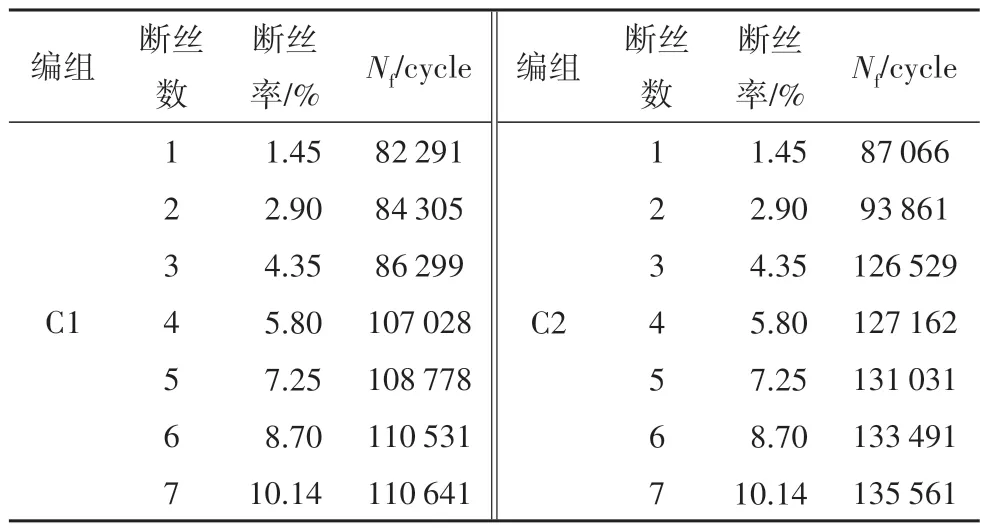
表2 试验索疲劳寿命测试结果Tab.2 Test results of fatigue life of test cable

3.2 模型参数

钢丝的均匀锈蚀深度dc可根据钢丝的平均锈蚀率（截面损失率）计算：

式中：D为钢丝直径；η为钢丝的平均锈蚀率.组成试验索的钢丝η=2.66%，计算钢丝的均匀锈蚀深度dc=33.5 µm.初始裂纹尺寸是由点蚀不均匀系数Rp确定的最大点蚀深度，即a0=dc×Rp.Li 等［14］根据乙酸盐雾加速腐蚀的Ф7mm 镀锌钢丝的点蚀深度，拟合得到A0=21 mm×π×7 mm 的钢丝点蚀不均匀系数的分布参数为μ0=4.708，α0=1.105.由式（9）可计算出钢丝长度为l0的Rp分布参数，当dc为定值时，a0具有与Rp相同的分布类型，即极值I型分布.

由式（4）可知，钢丝疲劳裂纹扩展系数B可由弹性模量E进行估算，两边取对数得：

式中：σff=（0.15～0.21）E.根据已有的测试结果［17］，钢丝的弹性模量服从对数正态分布，可知B亦服从对数正态分布.这里不考虑E的随机性，适当扩大系数B的取值范围，上限值σff取值为0.23E，下限值σff取值为0.13E，均值σff取值为0.18E.设B的上下限为均值加减标准差的3 倍，即认为B的母体中有99.87%的个体值将落入在上下限之间，计算可得B的变异系数约为0.19.

文献［12］给出了钢丝Kth和KC均值的估算方法.根据已有钢丝疲劳裂纹扩展的试验结果［16，18］，Kth和KC服从正态分布，变异系数近似取0.1.根据表1中未腐蚀钢丝的拉伸性能，估算试验索钢丝疲劳裂纹扩展速率模型参数并确定其分布类型如表3所示.

表3 试验索疲劳寿命预测模型参数Tab.3 Parameters of fatigue life prediction model of test cable

3.3 结果分析

为分析串联钢丝单元计算长度L0对拉索疲劳寿命的影响，分别将试验拉索的自由段划分为单元数n0=24、n0=12 和n0=1，即分别取L0=50 mm、L0=100 mm和L0=1 190 mm，采用全过程失效模拟方法，得到不同断丝率下的疲劳寿命.采用Mathematica 编制计算程序，Monte-Carlo 方法模拟次数为2 000 次，计算结果的均值与试验结果比较如图3所示.

图3 不同钢丝单元长度拉索断丝寿命均值Fig.3 Mean value of broken wire life of cable with different wire unit length

由图3 可看出，拉索断丝率随疲劳次数增加符合幂级数的增长规律，当拉索的断丝率达到10%之后，拉索的断丝率迅速增长而失去抵抗疲劳荷载的能力.串联钢丝单元划分得越多，拉索的疲劳寿命越短，这是由于单根钢丝串联模型中的“最弱联假定”所致.但这种趋势会随着钢丝单元数的增加而逐渐趋于稳定，因此n0=24 和n0=12 的计算结果已经十分接近.根据比较结果，如果将试验钢丝自由段视为一个单元，即n0=1，大部分试验数据落于曲线左侧且相差较大，将会导致评估结果不安全，但划分过多的钢丝单元将导致计算繁琐，结果过于保守.由于试验索长度较小，且钢丝数量较少，取n0=24（L0=50 mm）进行试验索的疲劳寿命预测.根据模拟计算结果，采用三参数Weibull 分布建立不同断丝率下的拉索疲劳寿命分布，不同断丝率的疲劳寿命累积概率曲线如图4所示.

图4 拉索疲劳寿命累积概率曲线Fig.4 Cumulative probability curve of fatigue life of cable

由图4 可知，随着断丝率的增加，疲劳寿命分布逐渐集中，差距也逐渐减小.基于上述计算结果得到拉索不同存活率下的断丝寿命，如图5 和表4 所示.由计算结果可知，存活率P=50%的断丝寿命与试验均值十分接近，证明本文的计算方法具有较好的精度；试验结果均在P=95%的预测范围内，用于工程实践是偏于安全的.

表4 拉索断丝寿命预测结果Tab.4 Prediction results of cable broken wire life

图5 不同存活率下拉索断丝寿命Fig.5 Broken wire life of cable under different survival rates

4 随机荷载下锈蚀拉索疲劳寿命评估

4.1 计算方法

4.1.1 锈蚀-疲劳竞争模型

根据大量钢材的大气暴露腐蚀数据，钢的大气腐蚀发展遵循幂函数规律［19］：

式中：dc（t）为t年后的累积腐蚀深度；tc为腐蚀的起始时刻；V为钢丝第1 年的腐蚀速率；κ为长期腐蚀指数，表征腐蚀的发展趋势.Karanci 等［20］根据温度、相对湿度、pH 值和Cl-浓度4 个变量，建立了带有径向基核函数的支持向量回归模型对钢丝的锈蚀速率进行预测.Feliu 等［19］统计了不同气候环境下金属的长期腐蚀数据.根据我国各地区的环境监测数据［21］，由Karanci 的预测模型和Feliu 的统计数据给出不同气候环境下钢丝锈蚀速率的参考值如表5所示.

表5 不同气候环境下钢丝锈蚀速率参考值Tab.5 Reference value of steel wire corrosion rate in different climatic environment

桥梁拉索在实际工程中始终受到腐蚀-疲劳耦合作用的影响，采用“速率竞争准则”表述锈坑（即点蚀深度）与疲劳裂纹间的相互关系［22-23］，如图6所示.由于锈蚀产物的积累，钢丝的锈坑增长是一个减速过程，即指数κ＜1，而疲劳裂纹的增长速率则随时间逐渐增大.早期锈坑的增长速率较高，疲劳裂纹始终追赶锈坑，此时锈蚀在钢丝损伤中占主导地位，即锈坑“溶解”疲劳裂纹.随着时间增加，理论上至少存在一个两者速率相等的时间点（tcom）使疲劳裂纹速率超过锈坑增长速率，而后疲劳效应占主导地位，直至钢丝断裂［24］.忽略t＞tcom时腐蚀对疲劳裂纹扩展速率的影响，以钢丝腐蚀速率以及点蚀深度的不确定性近似替代转换时间点tcom的不确定性，计算实际工程中锈蚀钢丝的疲劳寿命.

图6 锈坑增长与疲劳裂纹增长的竞争关系Fig.6 Competitive relationship between rust pit growth and fatigue crack growth

4.1.2 随机荷载下疲劳裂纹扩展

正常运营状态下拉索的荷载效应是随机的，拉索钢丝的应力幅随时间不断变化.与基于疲劳寿命曲线的疲劳损伤累积方法不同，基于裂纹扩展的疲劳寿命分析需要考虑荷载的作用次序，所以不能采用等应力幅作用来模拟.所有现行的计数法均未计及荷载循环先后次序的影响，因此荷载先后次序的影响总是存在的.但如果将荷载谱的周期取得短一些，则荷载先后次序对疲劳寿命的影响会减至最小程度，这一点已被荷兰国家宇航实验室的试验结果所证实［25］.此外，在疲劳荷载波动不大的稳态循环下，荷载先后次序对疲劳寿命的影响会进一步降低.拉索服役期的荷载波动主要由汽车荷载和风荷载引起，除极端天气或超重荷载外，其疲劳荷载的波动较小，因此对于随机荷载作用下的拉索疲劳分析仍可使用断裂力学方法.

应用雨流计数法对随机荷载进行处理后将得到荷载幅值和均值的二维随机变量，每个随机变量对应一次应力循环，因此需要计算每个应力循环作用下高强钢丝疲劳裂纹的扩展量.设荷载谱块内第i个随机变量对应的应力均值为σmi，应力幅为Δσi，根据疲劳裂纹扩展公式，控制疲劳裂纹扩展的主要是应力强度因子范围ΔK和应力比R两个参量，于是第i个应力循环所对应的ΔKi和Ri分别为：

式中：裂纹形状因子Y与裂纹深度a有关.当构件服役期较长包含很多数量的荷载谱块时，可认为在1个荷载谱块作用下裂纹尺寸不会发生较大变化，即可认为在1个荷载谱块内裂纹形状因子Y为定值.

根据式（16）和式（17）确定的ΔKi和Ri，应用裂纹扩展速率公式逐个对荷载谱块中每个元素进行计算，然后求和.施加一个包含mi个应力循环的荷载谱块的裂纹扩展量为：

式中：f（ΔKi，Ri）为荷载谱块内第i个应力循环所对应的裂纹扩展速率，即1 次应力循环所对应的裂纹扩展量.通过迭代计算得到每个疲劳荷载谱块作用后的累积裂纹长度和疲劳寿命：

式中：Δak为第k个荷载谱块作用的裂纹扩展量；ak为第k个荷载谱块作用后裂纹的累积长度；Nk为疲劳裂纹扩展寿命，即累积的谱块数量.由上述计算方法可知，随机荷载作用下钢丝的疲劳裂纹扩展计算，不考虑疲劳荷载谱块内应力循环的作用次序，但是计入了每个疲劳荷载谱块的作用次序，因此适用于长周期（包含较多谱块）的疲劳寿命计算.式（18）～式（19）与式（11）～式（12）近似，恒幅荷载计算时的计算步长相当于随机荷载下的一个疲劳荷载谱块，因此恒幅荷载作用下拉索疲劳失效的模拟方法依然适用.

4.2 拉索的疲劳荷载谱

将荷载-时间历程转化为一系列的荷载完整循环谱块，即得到构件的疲劳荷载谱，其中以雨流计数法应用最为广泛.本文采用“三峰谷计数原则”的简化雨流计数法计算斜拉索索力循环次数及其相应应力幅，其原理和方法相关文献已有详细介绍［26］，不赘述.

根据某斜拉索24 h 的索力监测数据获取其疲劳荷载谱.首先通过监测数据绘制包含完整峰谷值的索力时程曲线，对索力时程上所有转折点进行识别（前、后斜率相反的点）.根据拉索截面积计算相应的钢丝应力，过滤掉变幅小于1.5 MPa 的转折点，提取后所得的拉索应力时程如图7 所示.采用“三峰谷计数原则”的简化雨流计数法分析得到拉索的应力雨流矩阵如图8所示.

图7 拉索疲劳荷载效应转折点提取Fig.7 Extraction of turning point of cable fatigue load effect

图8 拉索应力雨流矩阵计算结果Fig.8 Calculation results of cable stress rain flow matrix

4.3 算例分析

某斜拉索规格为PES7-223，索长为218 m，拉索采用1670级7 mm高强镀锌钢丝，未腐蚀钢丝的拉伸性能试验结果如表6所示.

表6 拉索钢丝的力学性能Tab.6 Mechanical properties of cable steel wire

桥址位置参考武汉地区的气候环境特征（见表5），考虑到钢丝腐蚀的不确定性，假定V呈正态分布，均值为30.98 µm/a，变异系数为0.25，κ=0.4.取纤维束模型中串联单元长度L0=1 000 mm，单元数n0=218，由式（9）计算单元钢丝（A=1 000×π×7 mm2）点蚀不均匀系数Rp的分布参数.根据上述条件计算锈蚀拉索疲劳寿命分析模型参数如表7所示.

表7 锈蚀拉索疲劳寿命分析模型参数Tab.7 Parameters of fatigue life analysis model of corroded cable

拉索疲劳失效的临界断丝率取10%，即第22 根钢丝断裂时拉索失效，疲劳荷载谱采用如图7 所示的24 h 拉索应力雨流矩阵.根据图2 所示的计算流程编制Mathematica程序，采用Monte-Carlo 方法计算锈蚀拉索的疲劳寿命.采用极大似然法估计拉索疲劳寿命的分布参数，检验结果表明分布能够通过95%的K-S 的三参数Weibull 分布检验.其中dc（6）=63.44 µm 和dc（16）=93.91 µm 的疲劳寿命分布拟合计算结果如图9 所示，不同均匀锈蚀深度的拉索疲劳寿命概率分布比较如图10所示.

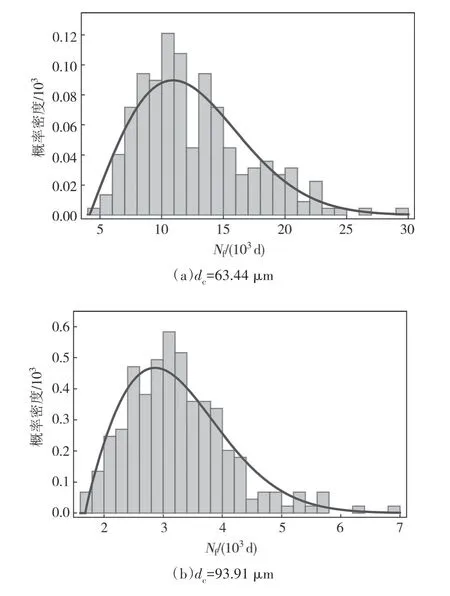
图9 锈蚀拉索疲劳寿命分布计算结果Fig.9 Calculation results of fatigue life distribution of corroded cables

图10 不同锈蚀深度的拉索疲劳寿命概率分布Fig.10 Probability distribution of fatigue life of cables with different corrosion depth

由计算结果可知，服役拉索一旦发生锈蚀，其疲劳寿命均值大幅下降，变异性减小，表明拉索的抗疲劳性能快速劣化.这种现象与钢丝抗裂纹萌生能力强、抗裂纹扩展能力弱有关.随着腐蚀程度的增加，裂纹扩展寿命在疲劳总寿命中的比例逐渐增大，裂纹萌生寿命逐渐减小，较大的点蚀深度尺寸使应力强度因子越过近门槛值低速区，直接进入稳态扩展区和快速扩展区，从而导致疲劳寿命的快速下降，且疲劳寿命分布更加集中.

以不同均匀锈蚀深度拉索疲劳寿命的概率分布曲线为基准，计算不同可靠度P下的疲劳寿命，并在对数坐标中进行线性拟合，可以得到拉索的P-dc-N曲线.其中P=50%的拟合结果如图11 所示，不同可靠度下锈蚀拉索的疲劳寿命预测曲线如图12 所示，曲线拟合参数如表8所示.

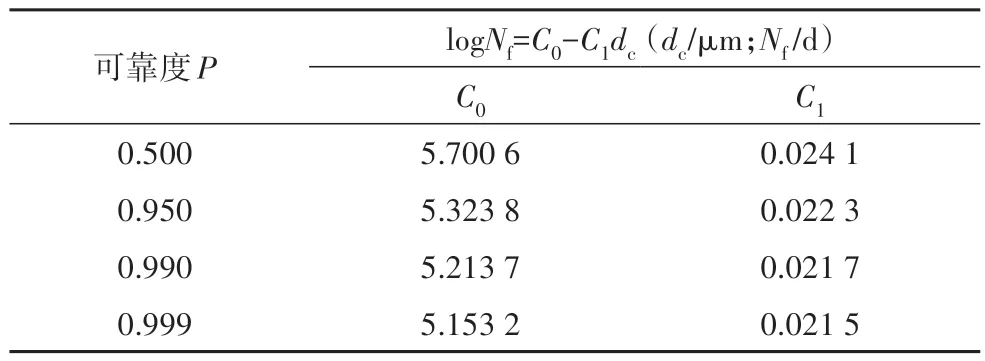
表8 锈蚀拉索疲劳寿命预测曲线拟合参数Tab.8 Fitting parameters of fatigue life prediction curve of corroded cable

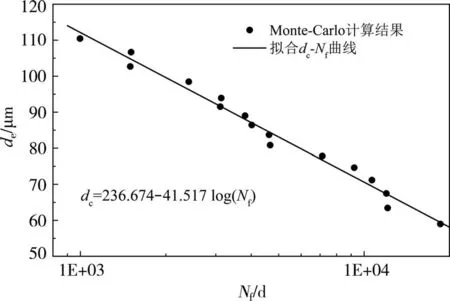
图11 锈蚀拉索疲劳寿命拟合结果（P=50%）Fig.11 Fitting results of fatigue life of corroded cable（P=50%）

图12 锈蚀拉索不同可靠度下疲劳寿命预测曲线Fig.12 Fatigue life prediction curve of corroded cable under different reliability

根据表8中的拟合参数可以对PES7-223型拉索在实测随机荷载作用下的疲劳寿命进行评估.取P=0.99作为目标可靠度，设拉索的设计寿命为30年，服役15 年后检测得到其钢丝的均匀锈蚀深度约为62µm，根据表8 中的参数计算目标可靠度下的疲劳寿命N0.99=7 336 d，大于拉索的剩余服役期ND=365 d/a×（30-15）a=5 475 d，可判定拉索的疲劳性能满足使用要求.也可计算出拉索满足剩余服役寿命的临界锈蚀深度或面积损失率直接与检测结果相比较，根据拉索的剩余服役期（或目标服役期）ND=5 475 d 计算可靠度P=0.99 下拉索钢丝的临界均匀锈蚀深度为67.84 µm，对应的拉索面积损失率为3.84%.如果此时拉索钢丝的均匀锈蚀深度大于67.84 µm，或拉索面积损失率的检测结果大于3.84%，可初步判定拉索的疲劳性能已不满足使用要求，应对拉索进行专项检测评估、维修加固或调整拉索的服役期.同时，也表明利用断裂力学方法计算拉索随机荷载作用下的疲劳寿命，需要准确掌握拉索钢丝的缺陷或腐蚀细节信息.

5 结 论

本文构建了基于裂纹扩展的锈蚀拉索疲劳寿命评估方法，分析了恒幅荷载和随机荷载作用下锈蚀拉索的疲劳寿命，得出如下结论：

1）基于钢丝的疲劳裂纹扩展速率模型，利用点蚀不均匀系数确定锈蚀钢丝的初始裂纹尺寸，将平行钢丝索视为一个多裂纹竞争的串-并联模型，通过全过程失效模拟方法得到锈蚀拉索的疲劳寿命.与试验数据比较，结果表明，该方法可以较为准确地预测拉索不同断丝率下的疲劳寿命.

2）拉索断丝率随疲劳次数增加符合幂级数的增长规律，当拉索的断丝率达到10%之后，拉索的断丝率迅速增长而失去抵抗疲劳荷载的能力.纤维束模型中的串联钢丝单元划分越多，拉索的疲劳寿命越短，但这种趋势会随着钢丝单元数的增加而逐渐趋于稳定.

3）锈蚀拉索的疲劳寿命服从Weibull分布.发生锈蚀后拉索疲劳寿命的均值大幅下降，变异性减小，其抗疲劳性能快速劣化.主要原因是冷拔钢丝的抗裂纹萌生能力强、抗裂纹扩展能力弱，点蚀效应缩短了裂纹萌生寿命，裂纹扩展寿命在疲劳总寿命中的比例增大，从而导致疲劳寿命的快速下降，且疲劳寿命分布更加集中.

4）通过雨流计数法将随机荷载历程转化为疲劳荷载谱块的重复作用，计算了不同腐蚀程度的拉索疲劳寿命.根据计算结果给出了Weibull 分布下的P-dc-N曲线，可对拉索服役期的疲劳可靠性进行评估，但应用时需要准确掌握拉索钢丝的缺陷或腐蚀细节信息.