基于路面识别的电磁混合式悬架自适应模糊控制

寇发荣， 贺嘉杰， 李孟欣， 许家楠， 武大鹏

(西安科技大学 机械工程学院,西安 710054)

传统汽车所采用的被动悬架以油液为介质，将路面冲击转化为热能耗散，难以应对复杂路况[1-4]。主动悬架减振效果良好，能够根据路面输入提供最优控制力，因此专家学者[5-8]对其进行了大量研究。

Hsieh等[9]在所设计的机械电子悬架基础上，通过具有开关模式的整流器(switch mode rectifier,SMR)控制电流，实现了悬架主动控制与能量回收。Rizvi等[10]基于整车主动悬架数学模型设计了鲁棒H∞控制器，将道路对车辆和乘客的干扰最小化，提高了整车的控制稳定性。石波等[11]基于直线电机-液压系统混合型执行器的主动悬架系统，设计了滑模控制器和馈能控制器，改善了悬架系统动力学性能且提高了能量回收效率。Zhang等[12]提出了一种泵式双筒馈能减振器，并设计了综合路面的预瞄控制算法，试验验证了该减振器的主动控制性能及能量回收潜力。汪若尘等[13]制定了天棚-地棚控制结合模糊PID(proportional integral derivative)的双环控制方案，实现了在改善车辆乘坐舒适性及操纵稳定性的同时回馈振动能量。但上述学者研究的主动悬架均聚集在单一路面等级上悬架的舒适性、安全性以及馈能特性，忽略了悬架在不同路面等级上的不同性能需求。

本文根据电磁混合式悬架工作原理，采用了BAS神经网络算法识别路面等级信息；设计了自适应模糊PID控制器，引入主动力反馈调整论域范围；针对各路面等级确定不同控制目标，并设计了相应的目标函数以合理制定模糊控制器规则，改善悬架系统的动态性能与馈能特性。

1 电磁混合式悬架结构与动力学模型

1.1 电磁混合式悬架结构及原理

电磁混合式作动器主要由直线电机与电磁阀式减振器构成，如图1所示。悬架系统在A级、B级路面时，直线电机作为发电机工作回收振动能量并产生电磁阻尼力，电磁阀式减振器输出可调阻尼力；在C级、D级路面时，直线电机作为电动机输出主动力，同时调节电磁阀节流口大小，实现复合主动控制。

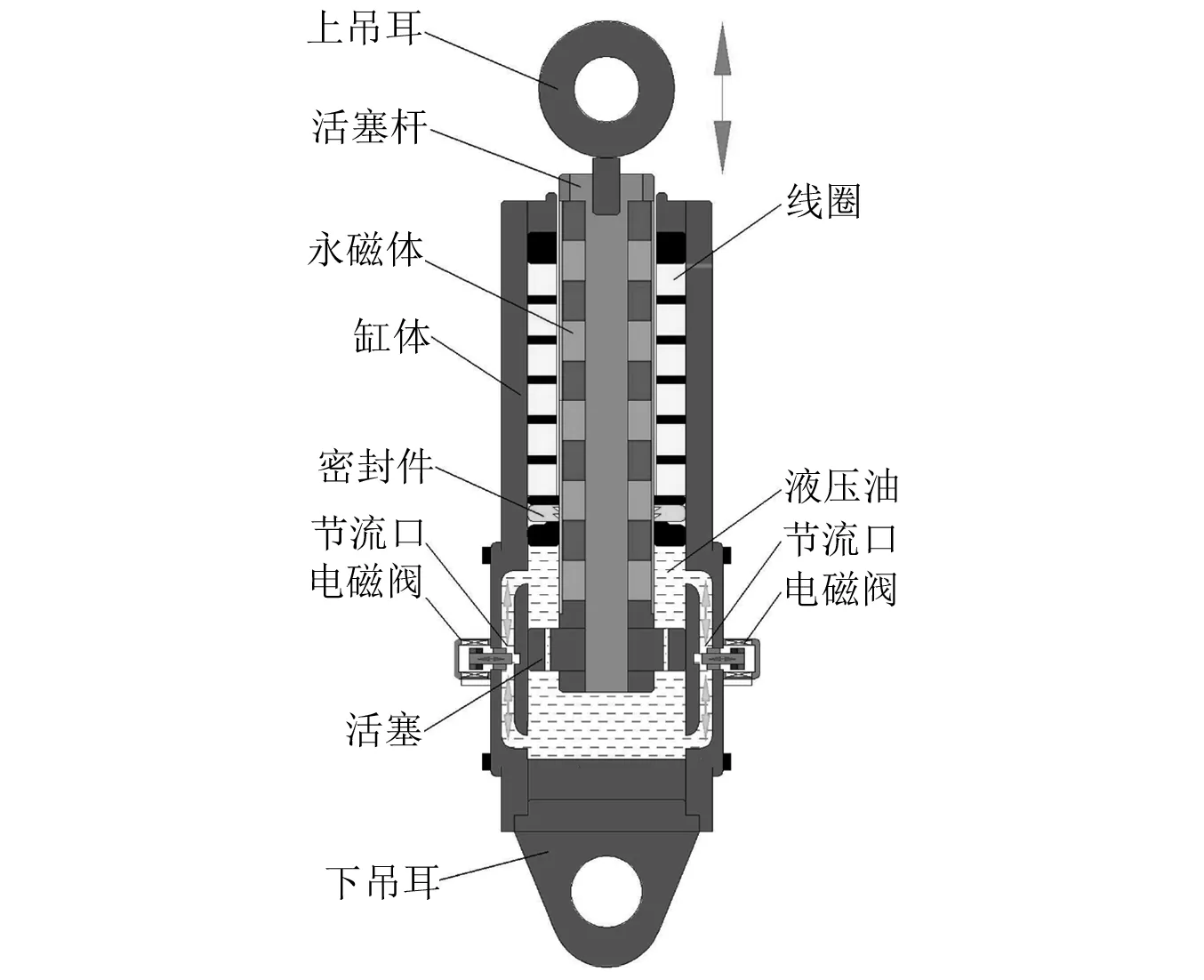
图1 电磁混合式作动器结构Fig.1 Electromagnetic hybrid actuator structure

1.2 电磁主动悬架动力学模型

电磁混合式悬架二自由度动力学模型，如图2所示。根据牛顿运动定律，建立悬架动力学方程组

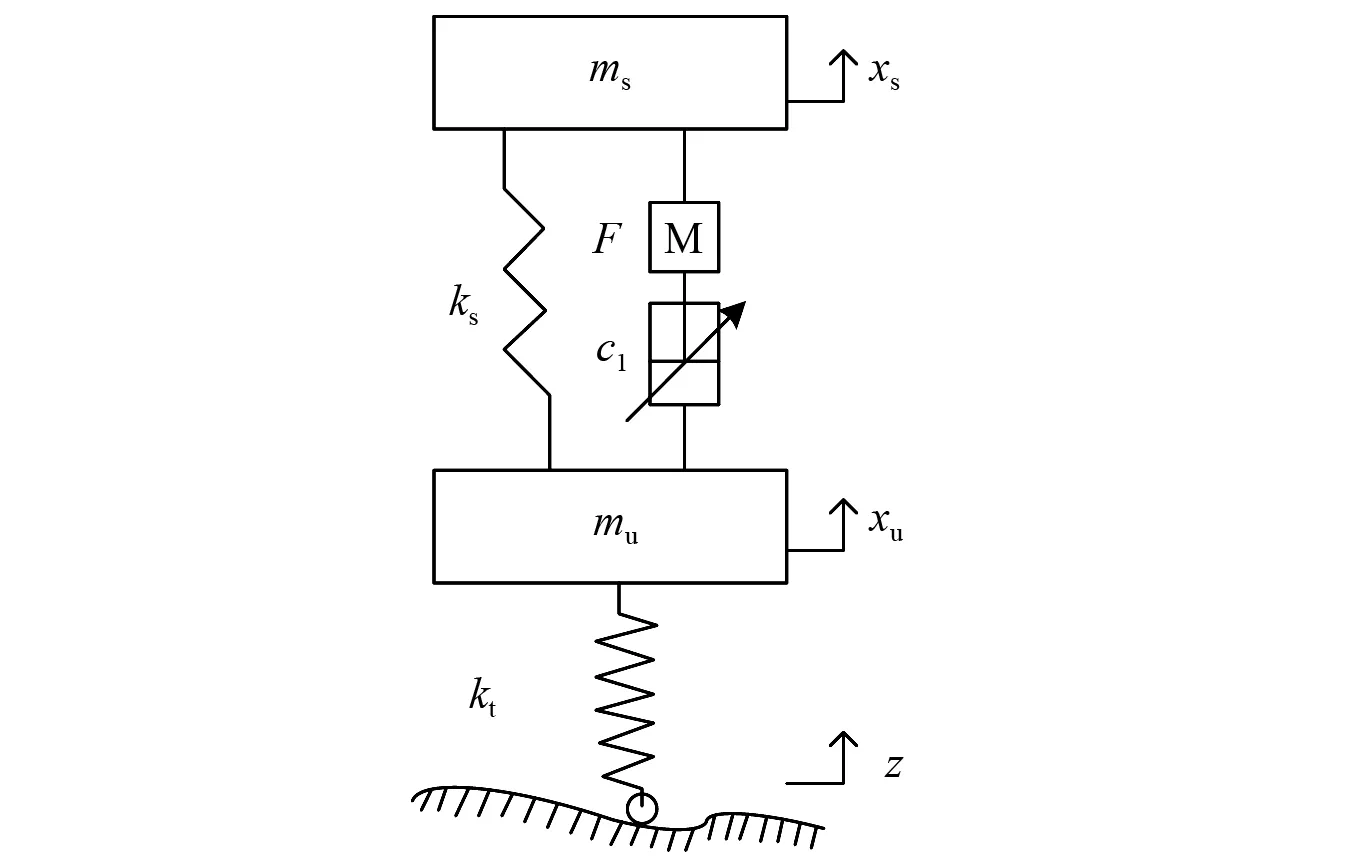
图2 二自由度混合式悬架动力学模型Fig.2 Dynamic model of two degrees of freedom hybrid suspension

(1)

式中：ms为簧载质量；mu为非簧载质量；c1为减振器阻尼系数；xu为非簧载质量位移；xs为簧载质量位移；F为电磁混合悬架输出控制力；ks为弹簧刚度，xs-xu为悬架动挠度；kt(xu-z)为轮胎动载荷。

1.3 直线电机数学模型

直线电机作为发电机工作时，电磁混合式作动器因路面激励，致使直线电机初级线圈和次级线圈相对运动，产生感应电动势。假设直线电机工作于发电机时为理想电机，产生的感应电动势表达式为

(2)

(3)

在路面激励下，悬架吸收的振动能量表示为

(4)

直线电机的馈能特性用馈能功率表示为

(5)

在工作时间T内，回收的能量P为

(6)

直线电机为发电机时，输出电磁阻尼力Fg为

Fg=kii

(7)

式中,ki为推力系数。

联立式(2)、式(3)、式(7)可得

(8)

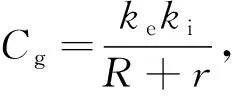
(9)

2 BAS-BP神经网络路面等级识别

2.1 路面等级分类

为准确描述路面起伏，使得路面信息更加接近真实路况，建立随机路面模型。选取应用最为广泛的滤波白噪声法，随机路面模型表达式为

(10)

式中：q(t)为路面位移；n0为空间频率；f0为下截止频率；G0(n0)为路面不平度系数；u为车速；W(t)为高斯白噪声。

根据路面不平度系数，将路面分为多个等级，如表1所示。

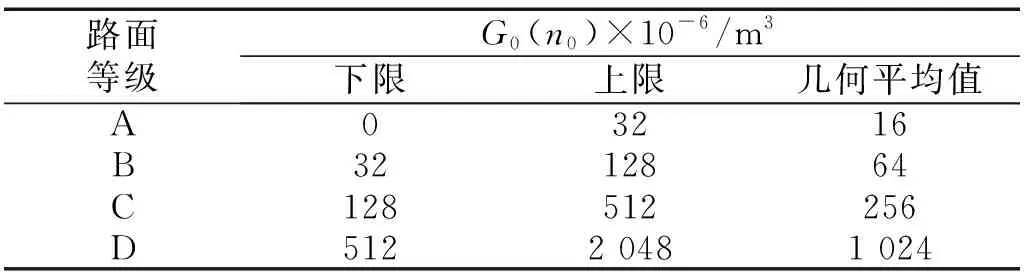
表1 路面等级分类标准Tab.1 Road level classification standard

2.2 BAS-BP路面等级识别模型

参照天牛须搜索算法优化BP神经网络权值和阈值的方法[14]，建立了基于BAS-BP神经网络算法的路面等级识别模型。通过车辆传感器获得不同路面等级下悬架响应数据，将相应的输入输出数据作为训练数据对BAS-BP神经网络进行训练，利用完成训练的BAS-BP神经网络模型识别路面等级。

BAS算法优化BP神经网络权值和阈值的具体流程如下：

步骤1初始化BAS算法参数，d0为两须之间的距离；xt为天牛在第t次迭代时的质心坐标；xlt,xrt为天牛左、右须在第t次迭代时的位置坐标；δ为步长；δt为第t次迭代时的步长因子；eta为变步长参数；k为空间维度；b为随机向量，b=rands(k,l)；

步骤2确定BP神经网络拓扑结构；

步骤3更新天牛及左右须位置坐标：

步骤4以训练数据的均方根误差MSE作为适应度函数进行BP神经网络的训练，即

(11)

式中：N为训练数据样本数；Yi为训练集第i个样本的模型输出值；yi为训练集第i个样本的实际值。

步骤5若满足迭代次数或精度要求，则进行下一步，否则，返回步骤4继续迭代；

步骤6输出优化后的权值和阈值。

BAS-BP优化BP神经网络流程图，如图3所示。BP网络结构确定为三输入层，单输出层，隐含层神经元个数的设置根据隐含层神经元经验公式h=0.5×(m+n)+a(a=1,2,…，10)可得，其取值范围为[3,12]。为提高模型识别准确性，依次比较各数值下的MSE值，确定最优值为9。天牛须搜索空间维度k为46，初始步长采用反复试验方法确定δ0=3，变步长参数eta=0.95，迭代次数为1 000代。将天牛须算法优化后的权值和阈值初始化BP神经网络，并在MATLAB软件中编写相应程序，导入簧载加速度、悬架动挠度和车轮垂直位移、路面不平度作为输入、输出数据，对BAS-BP神经网络进行训练，最终形成BAS-BP路面识别模型，识别路面等级。以相对误差及决定系数作为模型性能评价指标，相对误差越小，决定系数越接近1，表明模型性能越好，反之，则模型性能越差。BAS-BP神经网络算法适应度曲线，如图4所示。由图4可知,经过41次迭代BAS-BP算法即可获得最优解。由表2可得，以测试集为例，与BP神经网络相比，BAS-BP神经网络的相对误差、相关系数分别提高了3.67%、14.41%。

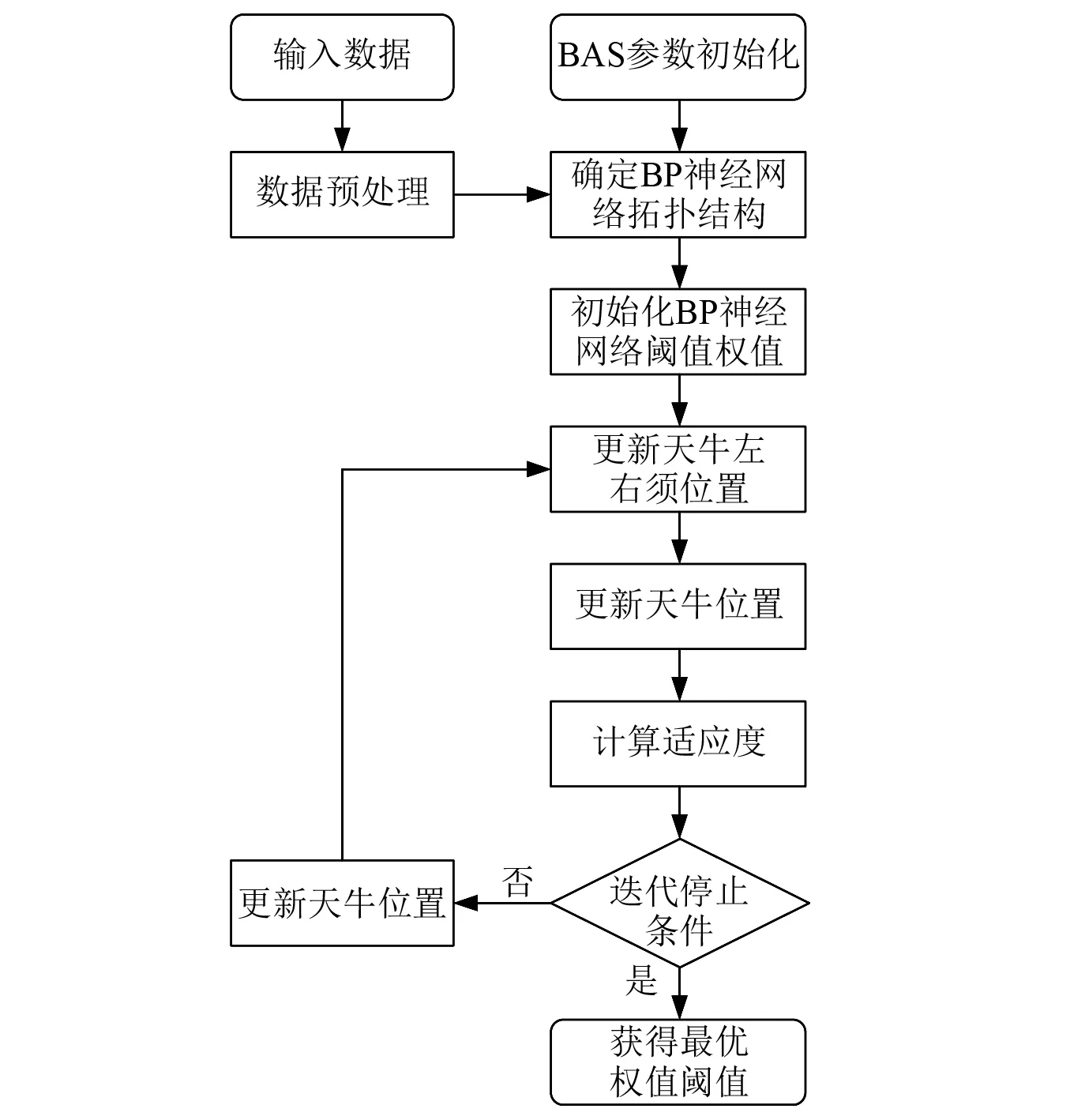
图3 BAS优化BP神经网络流程图Fig.3 Flow chart of BP neural network optimized by BAS

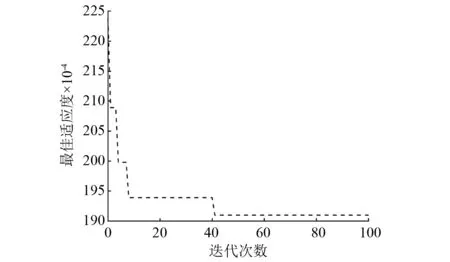
图4 BAS-BP神经网络适应度曲线Fig.4 BAS-BP neural network fitness curve

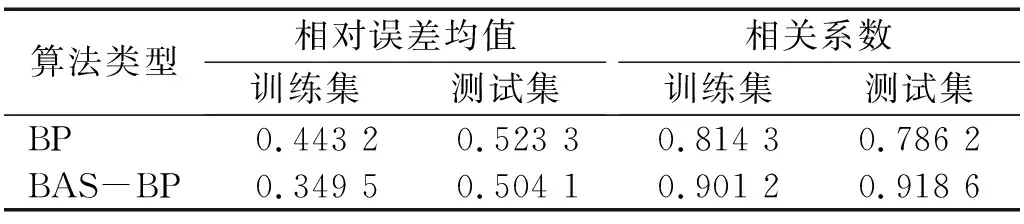
表2 BAS-BP路面识别模型数据Tab.2 Data of BAS-BP road surface recognition model

BAS-BP模型路面识别结果，如图5所示。由图5可知，BAS-BP模型实现了对路面等级的识别，随着路面等级的升高，路面激励增强，导致识别结果相对误差有所增大，但识别结果均集中于相应等级附近。

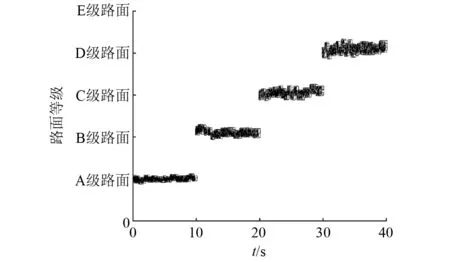
图5 BAS-BP模型路面识别结果Fig.5 Pavement recognition results of BAS-BP model

3 基于路面识别的自适应模糊PID控制器

为提高不同路面等级悬架的适应性，在路面等级识别结果的基础上，设计自适应模糊PID控制器，选择不同目标函数对控制器规则进行制定，使电磁混合式悬架能够在不同等级路面实现控制目标。

3.1 控制方案

我国道路路面等级分类为A～H级，实际道路主要分布在A、B、C、D四个等级，为制定控制器规则，针对不同路面等级设计了三种目标函数。A级路面行驶条件较为理想，以提高平顺性并回收振动能量作为控制目标；C级、D级路面起伏大，行驶条件差，应在尽可能的提高车辆操纵稳定性，保证车辆行驶安全性，以轮胎动载荷作为控制目标；B级路面较为平坦，行驶条件优于C级、D级路面，但差于A级路面，兼顾动态性能与馈能特性，故以提高综合性能为目标。

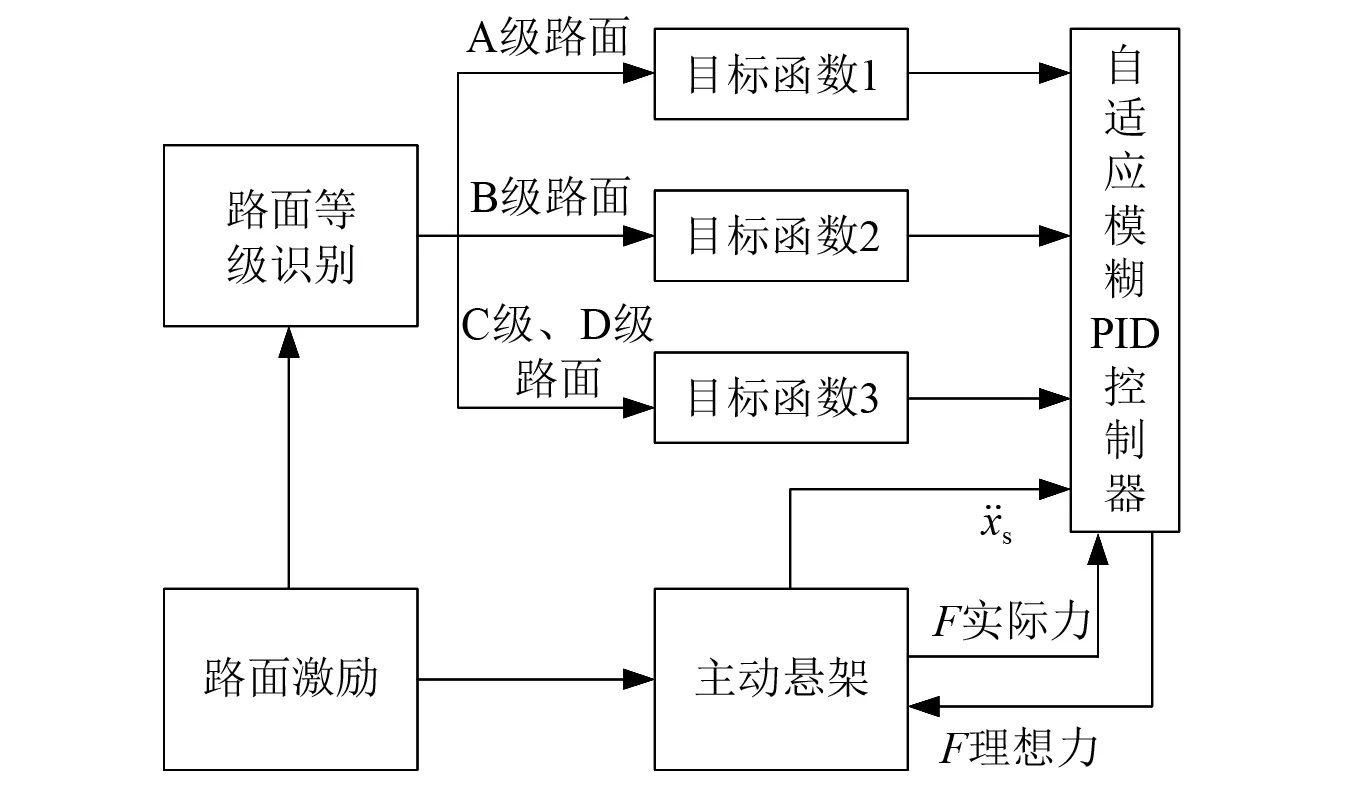
图6 自适应模糊PID控制方案Fig.6 Adaptive fuzzy PID control principle diagram

3.2 目标函数

A级路面：以提高平顺性与能量回收为目标，目标函数1如式(12)所示

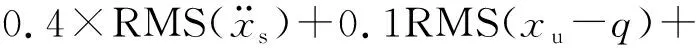
(12)

B级路面：提高综合性能，目标函数2如式(13)所示

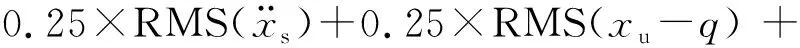
(13)

C级、D级路面：以提高车辆操纵稳定性为目标，故在目标函数中赋予轮胎动载荷更大的权重，目标函数3如式(14)所示

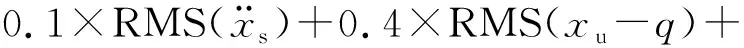
0.5×RMS(xs-xu)

(14)

3.3 变论域模糊PID控制器设计

本文在簧载质量加速度差值及其变化率作为模糊PID控制器输入的基础上，通过引入主动力反馈，建立变论域模糊控制器与参数调整模糊控制器以调整模糊PID控制器参数，使悬架系统在不改变输入输出基本论域的情况下，误差减小或增大时通过扩展或缩小论域范围提高控制精度。

以PID控制器参数P为例，其增量Δkp初始论域为[-Ep,Ep]，论域伸缩因子为αp，则可知伸缩后论域为[-αpEp,αpEp]，同理得Δki和Δkd伸缩后论域分别为[-αiEi,αiEi]和[-αdEd,αdEd]。论域伸缩过程如图7所示。

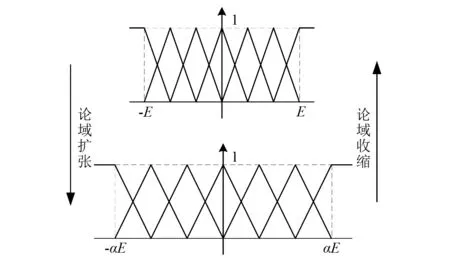
图7 论域伸缩过程图Fig.7 Domain scaling process diagram

对反馈的主动力进行归一化处理，取当前时刻主动力与混合式悬架输出最大主动力之比作为归一化后的主动力值。变论域模糊控制器的输入为实际主动力F，其模糊子集为{NB,NM,NS,Z,PS,PM,PB}，论域为[0,1]，为提高在快速冲击下系统的响应速度，实际主动力F的隶属度函数在论域两端的低速区划分稀疏，在论域中间的高速区划分稠密，如图8(a)所示。理想主动力与实际主动力差值ΔF模糊子集、论域均与F相同，由于低速运动力变化量较小，ΔF应对较大值敏感，更好的反馈理想主动力与实际主动力的差值，细化论域右端细化隶属度函数，如图8(b)所示。

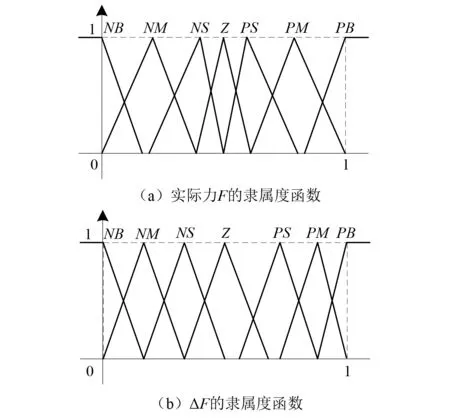
图8 F,ΔF隶属度函数Fig.8 F,ΔF membership function

参数调整模糊控制器输入为簧载质量加速度偏差e及其变化率ec，模糊子集为{NB,NM,NS,Z,PS,PM,PB}，基本论域为[-6,6]，隶属度函数选取三角函数并在论域内平均分布。

在自适应模糊PID控制器中，实际主动力F、理想与实际主动力差值ΔF作为变论域模糊控制器的输入，采用上述隶属度函数并结合αp，αi，αd模糊控制规则，通过重心法解模糊化后得到论域伸缩因子，以变化后的论域[-αpEp,αpEp]，[-αiEi,αiEi]，[-αdEd,αdEd]作为参数调整模糊控制器的输出论域，采用重心法解模糊化得到Δkp，Δki，Δkd从而调整PID控制器参数，自适应模糊PID控制器如图9所示。

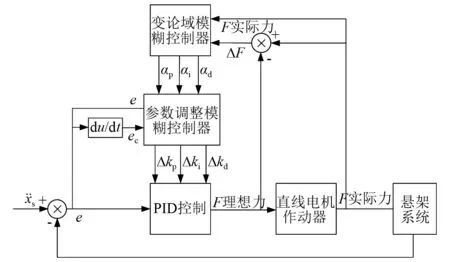
图9 自适应模糊PID控制器框图Fig.9 Adaptive fuzzy PID controller block diagram

在模糊控制中，模糊规则的合理程度直接影响着整个系统的控制精度。本文根据专家经验和目标函数，经过反复调试、仿真分析和归纳总结得到最终的模糊控制规则，以αp，Δkp为例，如表3、表4所示。

表3为αp模糊规则控制表，当F与ΔF较大时，控制减小误差，取较大控制量，所以输入论域取较大论域；当F与ΔF较小时，应缩小输入论域。结合F与ΔF特点将论域伸缩划分为不同区间：路面行驶条件理想，主动力及其差值较小时缓慢减小；路面条件良好，主动力与差值中等时缓慢增大；路面条件恶劣，主动力与差值较大时快速增大。

表3 αp模糊规则控制表Tab.3 αp fuzzy control rules

表4为Δkp模糊规则控制表，针对不同路面等级的控制目标，以式(12)、式(13)及式(14)作为A级、B级、C级、D级路面目标函数，控制目的均为降低目标数值，因此取函数最小值作为评判指标，不断仿真调试最终建立各路面等级上Δkp，Δki，Δkd的模糊规则。

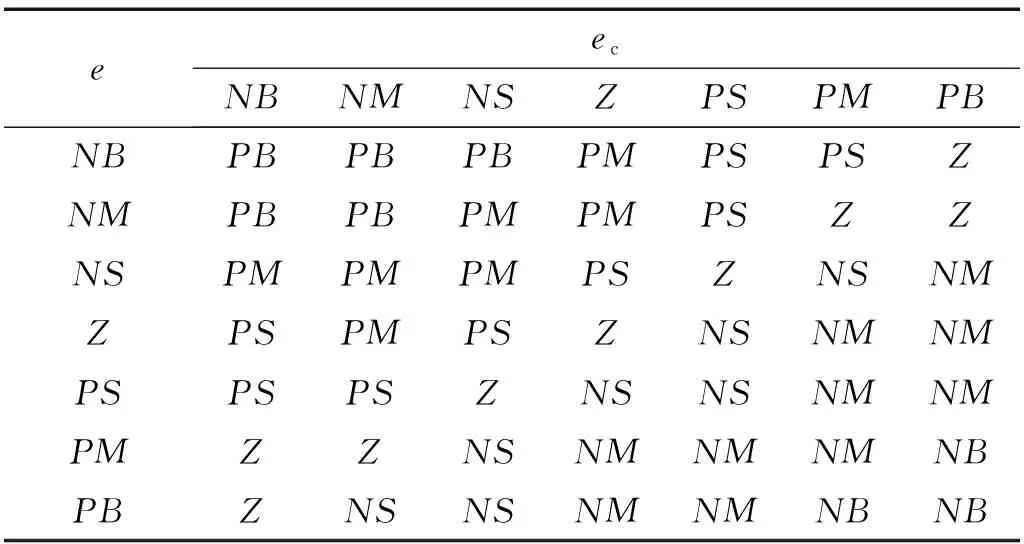
表4 Δkp模糊规则控制表Tab.4 Δkp fuzzy control rules

例如：一辆汽车以60 km/h行驶于A级路面，为实现A级路面的控制目标，则需根据目标函数1来控制悬架。确定输入输出的基本论域为[-6,6]，以输入e为NB，ec为Z为例，仿真分析输出Δkp在七种模糊子集情况下目标函数1数值大小，以其最小值为准则制定此时最佳规则为PM。

4 仿真分析

为验证所设计自适应模糊PID控制器的有效性，对比仿真分析被动悬架、模糊PID控制悬架与自适应模糊PID控制悬架。每隔5 s依次输入A级、D级、B级和C级路面以模拟随机路面等级，仿真分析悬架系统的动态特性。1/4车辆电磁混合式悬架仿真模型所用参数,如表5所示。

表5 1/4车辆悬架参数Tab.5 1/4 vehicle suspension parameters

4.1 动态特性

4.1.1 时域分析

对不同路面等级上的簧载质量加速度、轮胎动载荷时域响应进行分析，仿真结果如图10所示，均方根值对比如表6所示。同时对不同路面等级输入下的悬架动挠度进行分析，结果如图11所示。

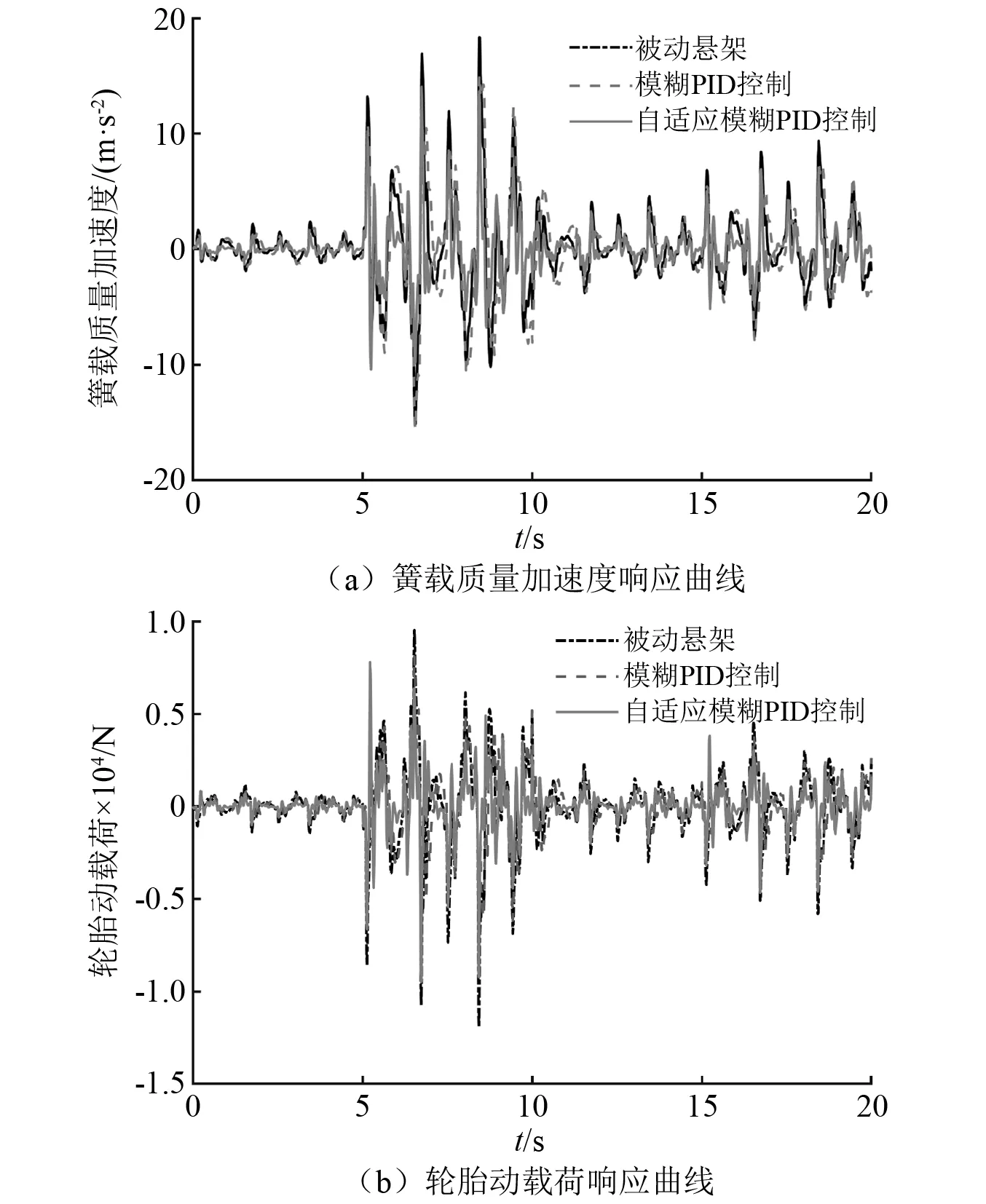
图10 电磁混合式主动悬架的动态时域响应曲线Fig.10 Dynamic time-domain response curve of electromagnetic hybrid active suspension

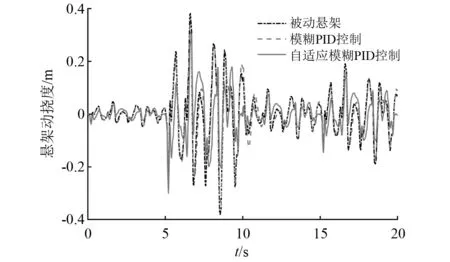
图11 悬架动挠度响应曲线Fig.11 Dynamic deflection response curve of suspension

由图10及表6分析可知:在0～5 s内，模糊PID控制的悬架相比于被动悬架簧载质量加速度降低了21.99%，自适应模糊PID控制的悬架在A级路面上控制目标为提高平顺性，簧载质量加速度相比于模糊PID控制的悬架降低了13.28%，悬架系统的平顺性得到了提升；在5～10 s内，模糊PID控制的悬架相比于被动悬架轮胎动载荷降低了13.16%，自适应模糊PID控制的悬架在D级路面上控制目标为提高车辆操纵稳定性，轮胎动载荷相比于模糊PID控制的悬架降低了15.54%；在10～15 s内，模糊PID控制的悬架相比于被动悬架簧载质量加速度、轮胎动载荷分别降低了11.33%、12.7%，自适应模糊PID控制的悬架在B级路面上控制目标为车辆综合性能，簧载质量加速度、轮胎动载荷相比于模糊PID控制的悬架分别降低了13.84%、9.09%；在15～20 s内，模糊PID控制的悬架相比于被动悬架轮胎动载荷降低了12.69%，自适应模糊PID控制的悬架在C级路面上控制目标为提高车辆操纵稳定性，轮胎动载荷相比于模糊PID控制的悬架降低了16.07%。

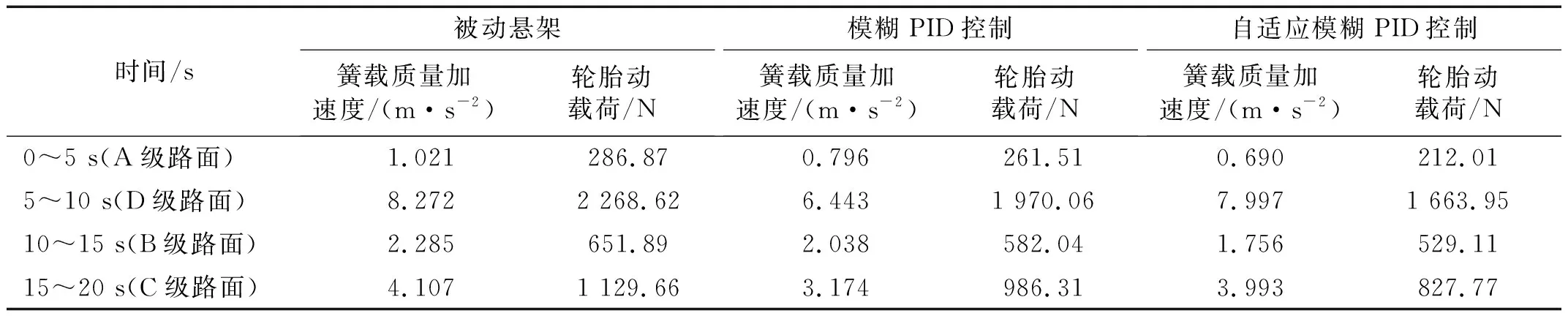
表6 各路面等级下悬架时域响应均方根值对比Tab.6 Comparison of root-mean-square time-domain responses of suspension at different pavement levels

在悬架动挠度方面，悬架系统设计最大值为70 mm，被动悬架最大值为37.8 mm，模糊PID控制下的电磁混合式悬架最大值为33.42 mm，自适应模糊PID控制下的电磁混合式悬架最大值为29.5 mm，相较于被动悬架降低了21.96%，更好地防止了与悬架行程极限点发生硬冲击的可能。

4.1.2 频域分析

仿真分析A级路面等级下簧载质量加速度、B级路面等级下簧载质量加速度与轮胎动载荷、D级路面等级下悬架动挠度以及C级、D级路面等级下轮胎动载荷的频域响应，结果如图12所示，并在人体频率共振区4～12 Hz内，以峰值衡量悬架性能改善程度，峰值对比如表7所示。

由图12及表7分析可知，在A级路面上，模糊PID控制的悬架相比被动悬架簧载质量加速度峰值降低了11.29%，自适应模糊PID控制的悬架相比于模糊PID控制的悬架簧载质量加速度峰值降低了18.6%，实现了控制目标，即提高了行驶平顺性；在B级路面上，模糊PID控制的悬架相比被动悬架簧载质量加速度与轮胎动载荷峰值分别降低了10.98%、10.79%，自适应模糊PID控制的悬架相比于模糊PID控制的悬架簧载质量加速度与轮胎动载荷峰值分别降低了12.47%、15.49%，提高了悬架系统的综合性能；在C级、D级路面上，模糊PID控制的悬架相比被动悬架轮胎动载荷峰值分别降低了19.96%、17.80%，自适应模糊PID控制的悬架相比于模糊PID控制的悬架轮胎动载荷峰值分别降低了16.81%、12.43%，提高了悬架操纵稳定性。在动挠度方面，为防止最大冲击下撞击限位块，故对D级路面进行仿真分析，结果表明自适应模糊PID控制的悬架相比被动悬架动挠度峰值降低了17.05%。

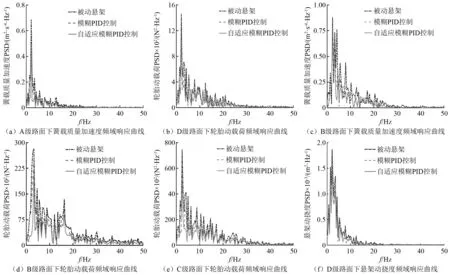
图12 电磁混合式主动悬架的动态频域响应曲线Fig.12 Dynamic frequency domain response curve of electromagnetic hybrid active suspension

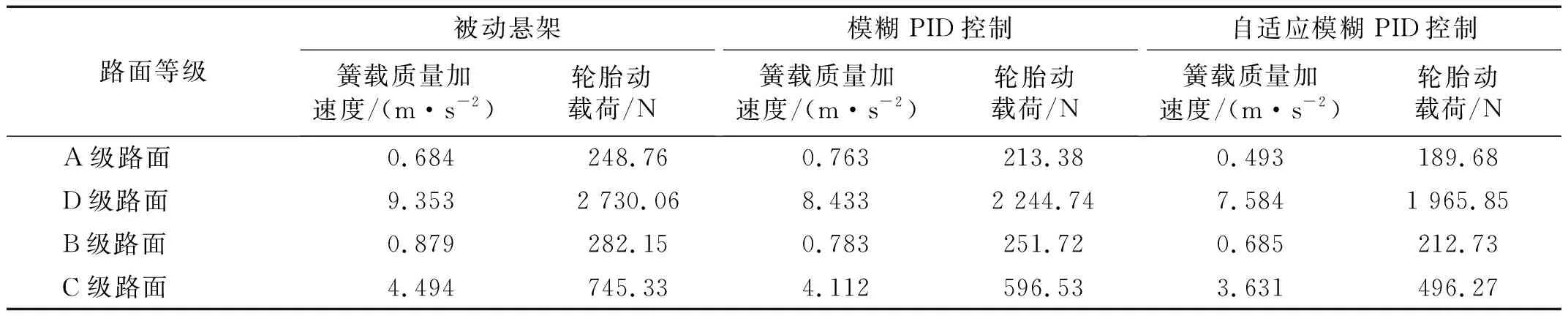
表7 各路面等级下悬架频域响应峰值对比Tab.7 Comparison of suspension response peaks in frequency domain under different pavement levels

4.2 馈能特性

以直线电机馈能功率衡量电磁混合式悬架的馈能特性，仿真各路面下的馈能功率，如图13所示。

图13表明：在A级、B级路面时，而在C级、D级路面无能量回收。电磁混合式悬架的馈能功率主要集中在100 W以下，峰值为238 W，馈能功率均方根值为42.8 W。

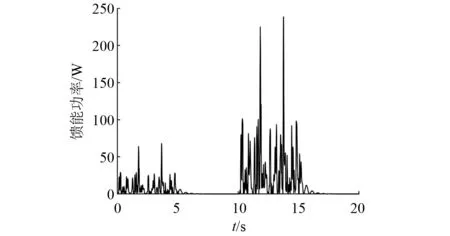
图13 电磁混合式悬架馈能功率图Fig.13 Energy regenerative power diagram of electromagnetic hybrid suspension

5 电磁混合式悬架台架试验

为验证自适应模糊PID 控制下的电磁混合式悬架的动力学性能及馈能特性，搭建电磁混合式悬架台架试验系统，试验台架如图14所示。该系统主要设备包括：液压振动台、上位机、dSPACE、加速度传感器、数据采集系统、驱动模块、能量回收装置等。

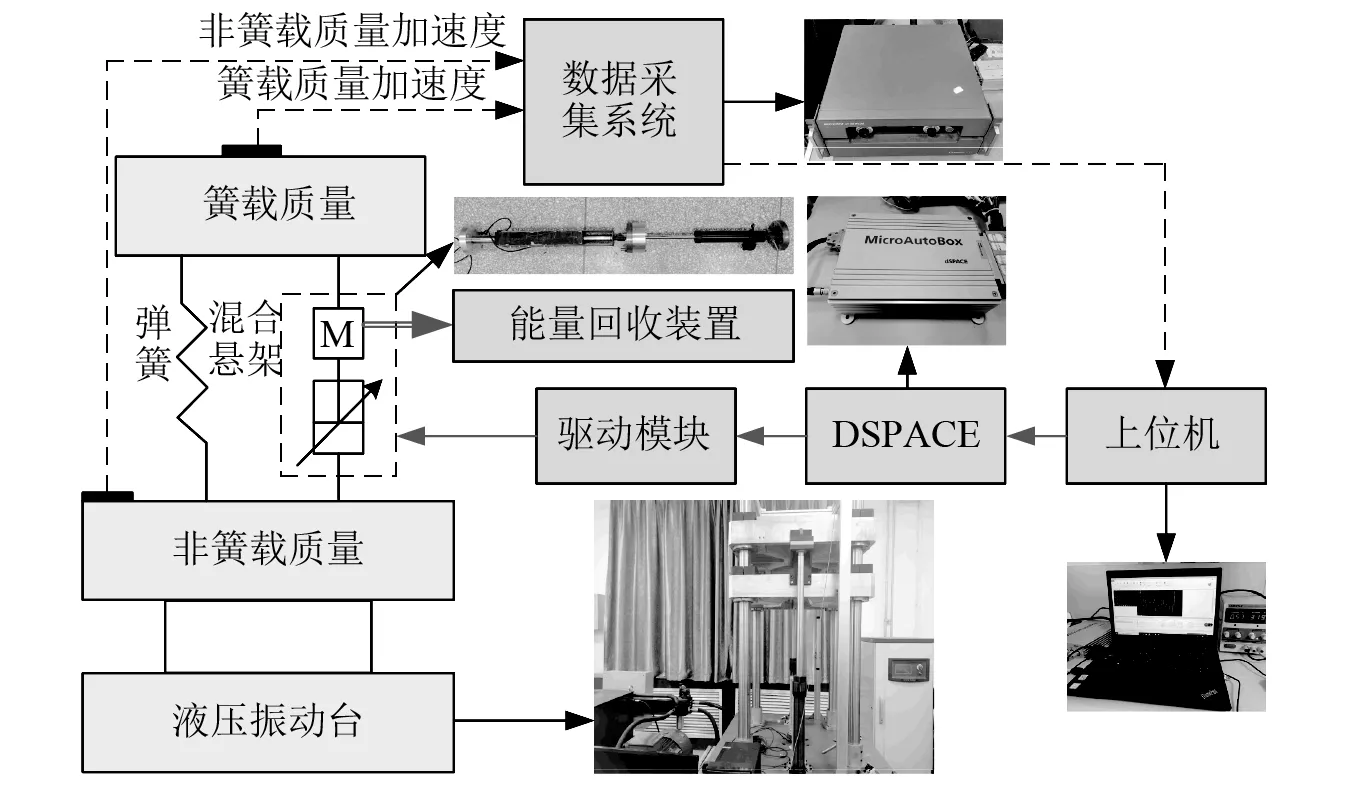
图14 电磁混合式悬架试验台架Fig.14 Electromagnetic hybrid suspension test bench

将A级、D级、B级、C级路面等级依次作为信号输入，如图15所示。在液压台架的控制下模拟路面工况，输出理想路面激励；数据采集系统实时采集加速度传感器数据，传输至dSPACE上位机，继而通过dSPACE调整电磁阀减振器与直线电机的控制电流，输出阻尼力以及主动力。

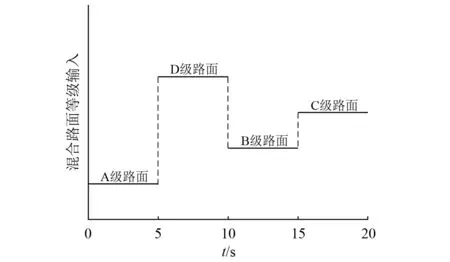
图15 混合路面等级输入Fig.15 Mixed pavement grade input

动力学性能及馈能特性的试验结果经数据处理后，将试验与仿真进行对比，如图16所示。具体分析图16(a)可知，各路面等级下试验与仿真时域簧载质量加速度均方根值相对误差分别为3.73%、15.19%、7.64%、13.55%；分析图16(b)～图16(e)可知，试验与仿真的频域簧载质量加速度峰值相对误差分别为9.04%、15.93%、11.89%、13.7%，时域与频域相对误差均在16%以内，试验结果与仿真结果基本一致。分析图16(f)可知，由于能量回收装置中的元器件消耗等因素的存在，试验与仿真结果的馈能功率均方根的相对误差为21.39%，试验中所回收的能量少于仿真结果，试验与仿真结果均表明悬架系统在A级、B级路面进行馈能，而在C级、D级路面几乎无能量回收。

图16 试验与仿真结果对比Fig.16 Comparison of experimental and simulation results

6 结 论

(1)根据电磁混合式悬架系统工作原理，建立了BAS-BP神经网络模型实现路面等级识别，针对不同路面等级设计了三种性能需求下的目标函数。

(2)为提高悬架系统在各路面等级上的适应性，设计了自适应模糊PID控制器，采用引入主动力反馈的变论域方法提高控制精度，从而输出最优主动力改善悬架系统性能。

(3)对电磁混合式悬架进行仿真分析与台架试验，结果表明，基于自适应模糊PID控制的电磁混合式悬架在A级路面上提高了平顺性，在B级路面上提高了综合性能，在C级和D级路面上提高了操纵稳定性，并回收部分振动能量，验证了自适应模糊PID控制的有效性。