计入箱体轴柔性的主减齿轮系统振动特性研究

周丽杰， 陈 凯， 范永琦， 柴召朋， 王义文

(1. 哈尔滨理工大学 机械动力工程学院，哈尔滨 150080; 2. 哈尔滨东安汽车发动机制造有限公司，哈尔滨 150060)

AT变速器是当前应用最广泛的变速器之一，其噪声、振动与声振粗糙度(noise, vibration and harshness, NVH)性能是评价汽车行驶安全性和驾驶舒适性的重要指标。在高档位AT变速器国产化的历程中，大量研究表明，其内部主减齿轮系统的啮合振动是变速器噪声超标的主要原因之一[1]。高档位AT变速器传动系统的结构形式特殊，主减驱动齿轮直接与轴承连接，轴承靠箱体轴支撑，箱体轴的薄壁结构使输入轴的刚度降低，进而引起额外的动态激励。特别地，主减齿轮系统多设计成大重合度斜齿轮传递，以降低啮合刚度激励程度，但重合度的分配又会进一步影响系统的振动响应。因此，揭示箱体轴柔性以及内外激励对主减齿轮系统动态响应特性的影响规律，对于提高国产变速器NVH性能具有重大意义。

当前，在齿轮传动系统动力学特性研究方面，国内外学者均采用集中参数法或有限元法。根据齿轮传动系统的特点，考虑将时变啮合刚度激励、误差激励、啮合冲击激励等非线性和时变性因素，建立不同类型的系统模型，进而分析系统的动态响应[2-4]。如Omar等[5]通过集中参数法建立了多自由度齿轮系统模型，考虑了系统动能、势能、内、外部激励，得到了不同参数变化时的齿轮系统动态响应。Shiau等[6]结合有限元法与广义多项式展开法，建立了扭转-横向耦合的混合动力学模型，研究了轴承刚度、阻尼、齿轮啮合位置对系统动力学特性的影响。常乐浩等[7]基于有限单元法，提出了一种考虑啮合刚度、齿轮误差和箱体柔性等因素影响的齿轮-轴-轴承-箱体耦合动力学模型。Yang[8]基于Newmark算法建立了多齿轮啮合传动系统模型，在考虑非线性齿侧间隙情况下，研究了传动系统在确定性载荷和随机载荷作用下的振动问题。

关于汽车变速器振动啸叫，主要通过考虑内部激励与外部激励对系统振动特性的影响进行研究。Park等[9]基于Romax软件建立了无级变速箱的整体系统模型，包括非线性啮合刚度、以及齿轮组件载体、壳体的柔性，分析了不同齿面接触形态对系统的影响。符升平等[10]通过集中参数法和有限元法，建立了汽车6AT变速箱齿轮轴与箱体的动力学耦合模型，通过分析齿轮轴系的动态响应测验模型危险区域的振动加速度。梅亚[11]基于Romax软件建立了4AT变速器模型，分析了齿轮与壳体柔性变形对齿轮传递误差、啮合错位量等啮合特性参数的影响。陈龙等[12]基于汽车发动机引起噪声阶次特征的特点，结合阶次追踪法，对汽车变速器加速工况振动信号进行阶次分析。

综上所述，现有文献多关注传统三轴式低档位变速器的动力学建模与振动激励研究。关于目前市场上主流产品——高档位含行星轮系的AT变速器研究很少，因此，研究其振动产生和传递的关键部件并分析其动态响应规律及影响因素具有重要的实际工程意义。本文针对某型号6AT变速器的主减齿轮系统，采用有限单元离散化建模方法，计入箱体轴柔性、静态传递误差激励以及不同重合度下斜齿轮时变啮合刚度的影响，建立了主减齿轮系统的弯-扭-轴-摆全耦合动力学方程。值得注意的是：此处的轴不是实体轴，而是轴向的一个自由度，即轴线方向的移动。分析了主减齿轮系统的固有特性，采用数值解法，获得不同工况和不同重合度下系统的振动响应特性，为变速器的减振降噪设计提供重要的理论支撑。

1 齿轮-轴承-转子系统动力学模型

某型号6AT变速器的动力是由液力变矩器传递给两排行星齿轮，然后由后排齿圈传递给一级主减齿轮系统。由于空间结构的特殊性，该齿轮系统也是引起自动变速器振动及噪声的主要原因之一。图1给出了齿轮系统结构示意图，该系统主要包括输入轴(输入花键和驱动齿轮)、输入轴轴承(角接触球轴承1对)、箱体轴、输出轴(从动齿轮、输出齿轮)、输出轴轴承(圆锥滚子轴承1对)。特别地，图1中黑白网格的零件具有盘状截面，并直接与箱体固接，为了与其他轴区分，将其命名为箱体轴。输入轴外表面固接输入花键和驱动齿轮，内表面与轴承外圈相配合，轴承内圈与箱体轴配合为静止部件，驱动齿轮与从动齿轮啮合后，动力经由输出齿轮传递给下级减速系统。

图1 主减齿轮系统结构示意图Fig.1 Schematic diagram of main reduction gear system

1.1 系统的有限单元法模型

上述齿轮传动系统尽管机械连接方式具有其特殊性，但仍然具有齿轮传动系统多自由度、质量连续分布、弹性单元组成的性质。因此，基于有限单元法，将齿轮传动系统离散为不同种类的单元，根据各单元节点耦合关系对各单元动力学矩阵进行组装，进而可求得各节点的动态响应。

图2为主减齿轮传动系统离散化结构有限单元模型。输入轴n上分为5个轴端节点(n1,n2,n3,n4,n5)，输入花键位于节点n1，驱动齿轮位于节点n3，输入轴n与箱体轴m之间是轴承单元连接。鉴于箱体轴m刚性较差，考虑轴柔性对驱动齿轮动态特性的影响，箱体轴m上分为5个轴端节点(m1,m2,m3,m4,m5)，节点m5与箱体之间是弹性连接。输出轴l上包括6个弹性轴段(l1,l2,l3,l4,l5,l6)，其中2个轴承单元(l2,l5)，从动齿轮节点l3与n3形成齿轮啮合单元。综上，整个输入齿轮传动系统共划分为16个节点，每个节点由空间的3个平动和3个转动自由度组成；考虑齿轮、轴承和转子的耦合关系以及转子的陀螺效应，该系统可由动力学矩阵进行耦合计算。

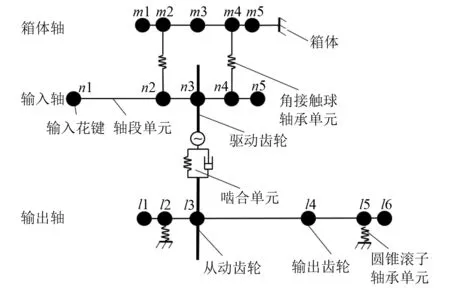
图2 主减齿轮系统有限单元模型Fig.2 Finite element model of main reduction gear system

1.2 轴段单元

1.2.1 箱体轴与输入轴连接处模型

如图2所示，轴端节点n2与m2,n4与m4分别通过角接触球轴承单元构成输入轴-轴承、箱体轴-轴承耦合单元，各节点位移向量可以表示为qsi=[xni,yni,zni,θni,φni,ψni,xmi,ymi,zmi,θmi,φmi,ψmi]T(i=2,4),式中:x,y,z分别为该节点处三个方向的位移；θ,φ分别为该节点x,y方向的转动角度;ψ为该节点z方向的扭转角度。其运动微分方程可以表示为

(1)

(2)

1.2.2 轴段单元模型

考虑轴的弯曲变形与扭转变形对齿轮系统动力学特性的影响，采用Timoshenko梁单元，建立弹性单元轴的12自由度运动微分方程。设第i个轴单元两侧的节点位移列向量qi=[xi,yi,zi,θi,φi,ψi,xi+1,yi+1,zi+1,θi+1,φi+1,ψi+1]T(i=m1,…,m5;n1,…,n5;l1,…,l5)，则轴段单元运动方程可以表示为

(3)

式中，Mi,Ki,Ci分别为第i个轴段单元的质量矩阵，刚度矩阵和阻尼矩阵。采用经典的Rayleigh阻尼来计算Ci，其表达式为

Ci=uMi+wKi

(4)

式中:u为质量比例系数;w为刚度比例系数。

1.3 齿轮啮合单元

1.3.1 啮合单元运动微分方程

针对输入端外啮合斜齿轮副，建立其弯-扭-轴耦合的12自由度动力学模型，齿轮副啮合状态简化为弹性弹簧与阻尼器耦合作用。如图3所示，驱动齿轮和从动齿轮分别表示为p(即为图2中n3)和g(即为图2中l3)，其齿轮半径分别表示为rp和rg;βpg为斜齿轮的螺旋角；φpg为系统y轴正方向与啮合面的夹角。则斜齿轮副的位移列向量可表示为qsp=[xp,yp,zp,θp,φp,ψp,xg,yg,zg,θg,φg,ψg]T。

图3 齿轮啮合模型Fig.3 Gear meshing model

将两齿轮各位移向量沿啮合线方向投影，得出斜齿轮时变相对总变形为

σ(t)=Vqsp-e(t)

(5)

式中:e(t)为齿轮静态传递误差;V为两齿轮的投影矢量，可表示为

V=[cosβpgsinφpg,cosβpgcosφpg，sinβpg，

-rpsinβpgsinφpg,-rpsinβpgcosφpg,rpcosβpg,

-cosβpgsinφpg,-cosβpgcosφpg,-sinβpg,

-rgsinβpgsinφpg,-rgsinβpgcosφpg,rgcosβpg](6)

根据牛顿第二定律，啮合单元的时变运动微分方程为

式中:mp,mg分别为驱、从动齿轮质量；Iψp,Iψg分别为驱、从动齿轮的转动惯量；wp,wg分别为驱、从动齿轮角速度；Tp,Tg分别为驱、从动齿轮转矩(取顺时针方向为正)；k(t)为时变啮合刚度；c(t)为时变啮合阻尼。

则上述微分方程的矩阵表达式为

(8)

式中:Mm,Cm,Km分别为齿轮啮合单元的质量矩阵、阻尼矩阵和刚度矩阵；Gm为陀螺矩阵；Fe为时变冲击力；FT为载荷激励力，且FT可由(9)给出。

FT=[0,-mpg,0,0,0,Tp,0,-mgg,0,0,0,-Tg]T

(9)

1.3.2 时变啮合刚度分析

由于空间螺旋线的存在，斜齿轮的啮合刚度不仅随着齿廓啮合位置的不同存在时变性，而且受端面重合度和轴面重合度的影响。

此处采用的圆柱斜齿轮其总重合度εγ为3.0，根据近似替代理论，当总重合度较大时，斜齿轮的理论啮合刚度可近似表达为总的齿轮副接触线长度和单位面积上轮齿啮合刚度的乘积[13]。

k′(t)=ka·l(t)

(10)

式中:ka为在单位面积上轮齿啮合刚度;l(t)为总的齿轮副接触线长度。

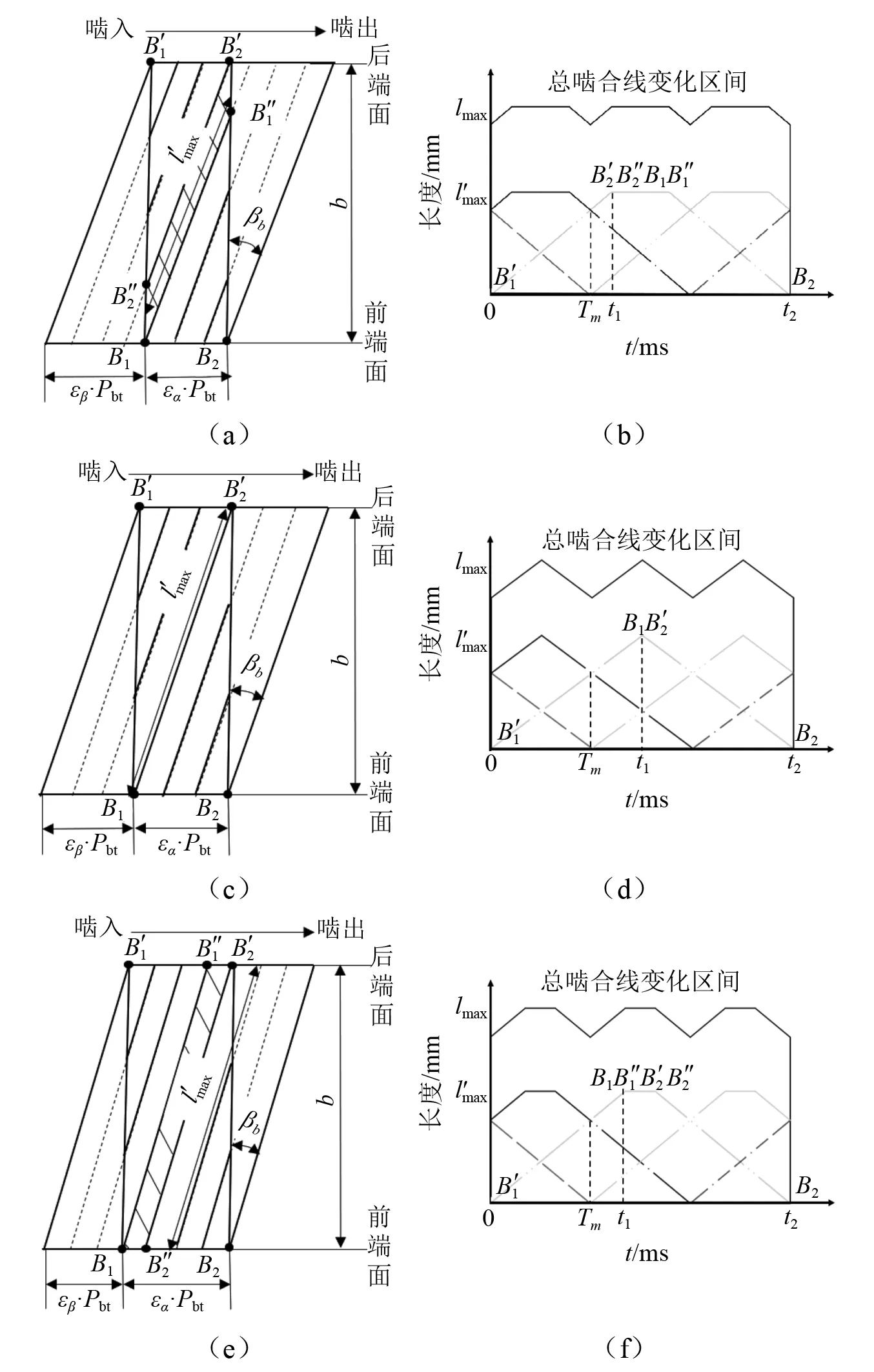
图4 三种齿轮接触模型及啮合区域的接触线分布图Fig.4 Three kinds of gear contact models and contact line distribution diagram of meshing area

以下分三种情况，分别求解l(t)的表达式：

当εα<εβ时，

(11)

当εα=εβ时，

当εα>εβ时，

(13)

上述理论啮合刚度k′(t)的周期性函数可以展开为同周期的傅里叶函数，与其相对应的时变啮合刚度k(t)表示为

(14)

式中，km为平均啮合刚度，由ISO-6336求解。其中,an,bn与理论啮合刚度的关系为

(15)

取傅里叶函数六阶多项式进行对比，得到三种不同重合度组合((a)εα=1.44,εβ=1.56；(b)εα=1.50,εβ=1.50；(c)εα=1.56,εβ=1.44)的时变啮合刚度拟合曲线，结果如图5所示。从图5中可以看出，(b)组合时变啮合刚度的幅值变化区间最大，(a)组合和(c)组合幅值波动的区间较小。

图5 三种时变啮合刚度拟合曲线图Fig.5 Fitting curves of three time-varying meshing stiffness

1.3.3 齿轮静态传递误差分析

齿轮在制造与安装过程都会产生误差，对齿轮动力传递有很大影响。传递误差的大小为实际啮合位置与理论啮合位置在啮合线上的差值，齿轮传递误差可以按啮合频率进行傅里叶级数展开，表示为

(16)

式中，e0为平均传递误差，取值为0。

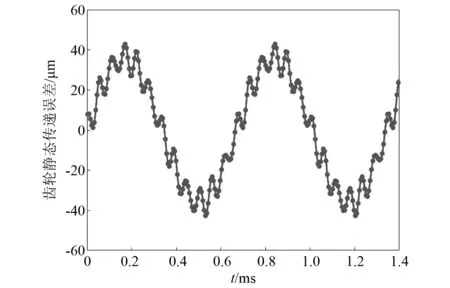
图6 齿轮静态传递误差曲线图Fig.6 Static transmission error curve of gear

1.4 轴承-基础单元

输出轴上的圆锥滚子轴承与箱体直接相连，轴承的刚度和阻尼是系统建模须考虑的重要因素。由于箱体刚性较大，轴承的轴向刚度与径向刚度可视为常数；轴承的相对质量较轻，固不考虑轴承质量对系统动态特性的影响。设轴l与轴承耦合的第j个节点位移列向量为qst=[xlj,ylj,zlj,θlj,φlj,ψlj](j=2,5)。则轴承-基础单元的运动微分方程为

(17)

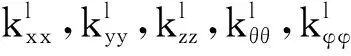
(18)

1.5 齿轮系统动力学模型

根据有限单元法理论，将轴段单元子阵、齿轮啮合子阵与轴承支承子阵，式(1)、式(3)、式(8)、式(17)组装到整体矩阵中，将主减齿轮系统的动力学模型表示为

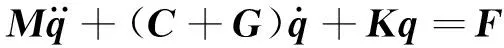
(19)

式中:q为所有节点位移列向量;M,C,G,K分别为组合质量矩阵、阻尼矩阵、陀螺矩阵、刚度矩阵；F为组合激励力。主减齿轮系统划分为16个节点，输入轴与箱体轴通过轴承单元进行耦合，输入轴与输出轴通过齿轮啮合单元进行耦合，依据系统整体节点编号与各单元局部节点编号对应关系将轴段单元、齿轮啮合单元、轴承-基础单元组装到系统中，系统矩阵组装规则如图7所示。

图7 主减齿轮系统矩阵组装规则图Fig.7 Main reduction gear system matrix assembly rule diagram

式(19)中的系数为时变的周期性函数，采用Newmark-β积分算法对其进行求解[15]。此算法对线性加速度算法进行了修正，在t+Δt时刻的位移列向量和速度列向量中引入控制参数γ1，β1，如下式

(20)

(21)

式中，Δt为积分步长，考虑方程稳定性令γ1=0.5，β1=0.25。根据式(20)和式(21)可得：

t+Δt时刻的主减齿轮系统动力学模型方程为

(22)

(23)

2 齿轮传动系统振动特性分析

上述齿轮-轴承-转子耦合系统在传动过程中，斜齿轮啮合刚度和啮合误差动态激励将导致各节点的6自由度振动，其中齿轮节点的扭转振动和相对位移振动尤为突出。在建模中，由于考虑了箱体轴柔性与输入轴的耦合作用，系统的模态响应和动态响应均发生变化；同时齿轮重合度的变化与时变啮合刚度直接相关，影响系统的振动响应幅值。将某型号6AT变速箱主减齿轮系统主要结构参数(表1)代入上述系统非线性耦合模型中，并进行求解。

表1 某型号6AT变速箱主减速齿轮系统结构参数Tab.1 Structural parameters of the main reduction gear system of a 6AT transmission

2.1 固有特性分析

不考虑系统阻尼和外部激励，变速箱传动系统的实际转速范围为500～6 500 r/min，分别计算出未考虑箱体轴的66自由度传动系统和耦合了箱体轴后(考虑了箱体轴各节点30个自由度)的96自由度传动系统前15阶固有频率和模态振型，结果如表2所示。对比结果发现，耦合箱体轴后系统的固有频率在4阶之后呈现明显的减小趋势。这主要是由于将输入轴的轴承连接到箱体轴上，箱体轴的柔性增加了输入轴的柔性，导致系统的部分固有频率降低。对比不同阶次下模型中相近的固有频率，它们的振型比较接近，如未耦合箱体轴的第4阶固有频率与耦合箱体轴的第5阶固有频率，未耦合箱体轴的第7阶固有频率与耦合箱体轴的第9阶固有频率；但耦合箱体后出现了一些新的振型，如第8阶的x,y向移动，第10阶的x,y向弯摆振动。这是由于箱体轴代入的自由度使系统呈现更多的联合共振振型。由此表明，将箱体轴计入系统模型更能反应主减齿轮的振动特性。

表2 固有频率与振型Tab.2 Natural frequency and mode shape

2.2 不同工况下系统振动响应分析

对齿轮传动系统的动态特性进行分析，当输入转速逐渐递增，负载为150 N·m时，分别测量输入轴上n2,n3,n4节点，输出轴上l2,l3,l4节点的振动位移幅值，结果如图8所示。从图8中可以看出，各节点的振动幅值随着转速的增加而增加，且两端轴承与啮合齿轮具有相同的变化趋势。当输入转速为2 910 r/min，3 290 r/min，3 920 r/min，4 910 r/min，5 760 r/min时，节点的振动幅值有凸起。当转速为3 290 r/min和3 920 r/min时，激励频率成分为3/2fm和fm(fm为啮合频率)，与系统的第32阶(4 222.9 Hz)和27阶固有频率(3 461.4 Hz)相接近，从而使系统节点的振动有所凸起。当转速为2 910 r/min和5 760 r/min时，激励频率成分为2fm和fm，与齿轮系统的第36阶固有频率(5 001.9 Hz)接近，激起系统以y向的弯扭振动为主的振动形式，但其能量不大。当转速为4 910 r/min时，驱动齿轮节点、输出齿轮节点和输出轴承节点振动的幅值明显增加，系统出现凸起的共振峰，由于输入轴承节点n2,n4与箱体轴直接相连，箱体轴的柔性弱化了该节点的振动强度，使其幅值降低。

图8 输入轴与输出轴重要节点的速度-位移图Fig.8 Velocity-displacement diagram of important nodes on input and output axes

进一步，保持传动系统工况不变，仍采用升速的形式(间隔为250 r/min)，在不同转速下获取啮合齿轮节点n3和l3在啮合线方向相对振动幅值的频谱，得出齿轮系统的阶次分析图，结果如图9所示。从图9中可以看出，齿轮系统阶次幅值在fm和2fm处幅值高值明显，并在3/2倍频阶次处也出现了较高幅值，但其能量较小；随着转速的增加各阶次的幅值频率随之增加，最高峰值出现在5 000 r/min附近(与图9的4 910 Hz)对应，激励频率fm对应系统的第32阶固有频率(4 222.9 Hz)，2fm对应系统的45阶固有频率，激起系统x,y向弯扭摆振动为主的振动形式，此时系统共振十分明显。

图9 齿轮啮合处位移瀑布图Fig.9 Displacement waterfall diagram of gear meshing

对输出齿轮施加三种不同扭矩载荷80 N·m，150 N·m和220 N·m时，啮合线方向相对振动位移幅值与转速的关系，如图10所示。当输入转速在500～2 200 r/min时，相对位移的幅值波动较小，其大小随着载荷的增加成正比增加。这是由于随着系统外部激励增加，静态传递误差变大，引起时变冲击力与载荷激励力增大，导致振动加剧。当输入转速在2 200～6 500 r/min时，系统在共振点峰值处的相对位移幅值随着载荷的增大而增大，但增幅较小。这主要是由于峰值的激增主要受固有频率下的模态振型影响，系统载荷作为外部激励影响占比相对减弱。综上，对于主减齿轮系统的动态响应，随着外加负载的增加而增强，但在共振点处增量值受共振频率下的振型影响，增幅较小。

图10 三种不同扭矩的速度-位移图Fig.10 Speed-displacement diagram of three different torques

2.3 不同重合度下系统动态响应

进一步，当端面重合度不变时，研究主减齿轮不同轴向重合度对动态特性的影响规律。此处端面重合度(εα)取1.56，轴向重合度(εβ)分别取0.64, 1.04, 1.44，齿轮啮合线方向相对振动位移幅值与转速的关系,如图11所示。随着轴向重合度的增加，系统的相对位移幅值减小；这主要是由于重合度增加，时变啮合刚度的平均值和波动幅值减小，使系统的动态响应减弱。特别地，在共振点4 910 r/min处，系统的振动能量随着轴向重合度的增加明显减弱，相对位移幅值降低幅度最大。

图11 三种不同轴向重合度的速度-位移图，端面重合度1.56Fig.11 Velocity-displacement diagram of three different coaxial coincidence degrees with end face coincidence degrees of 1.56

考虑主减齿轮系统总重合度为3.0，针对图5所示的三种不同的端面重合度和轴向重合度组合，研究系统的动态响应规律，结果如图12所示。当输入转速在500～6 500 r/min时，可以看出三组啮合线方向相对位移幅值变化趋势一致，(b)组合位移幅值最大，(a)组合次之，(c)组合最小。在共振转速处，随着重合度组合的改变其相对位移幅值增幅变大；这主要是由于(b)组合的时变啮合刚度波动幅值较其他两组更大，导致所有振区间的振动均加剧，且共振区间振动更加剧烈；(c)组合的时变啮合刚度波动幅值较小，且其平均啮合刚度较大，所以在各转速下的振动能量相对较弱。

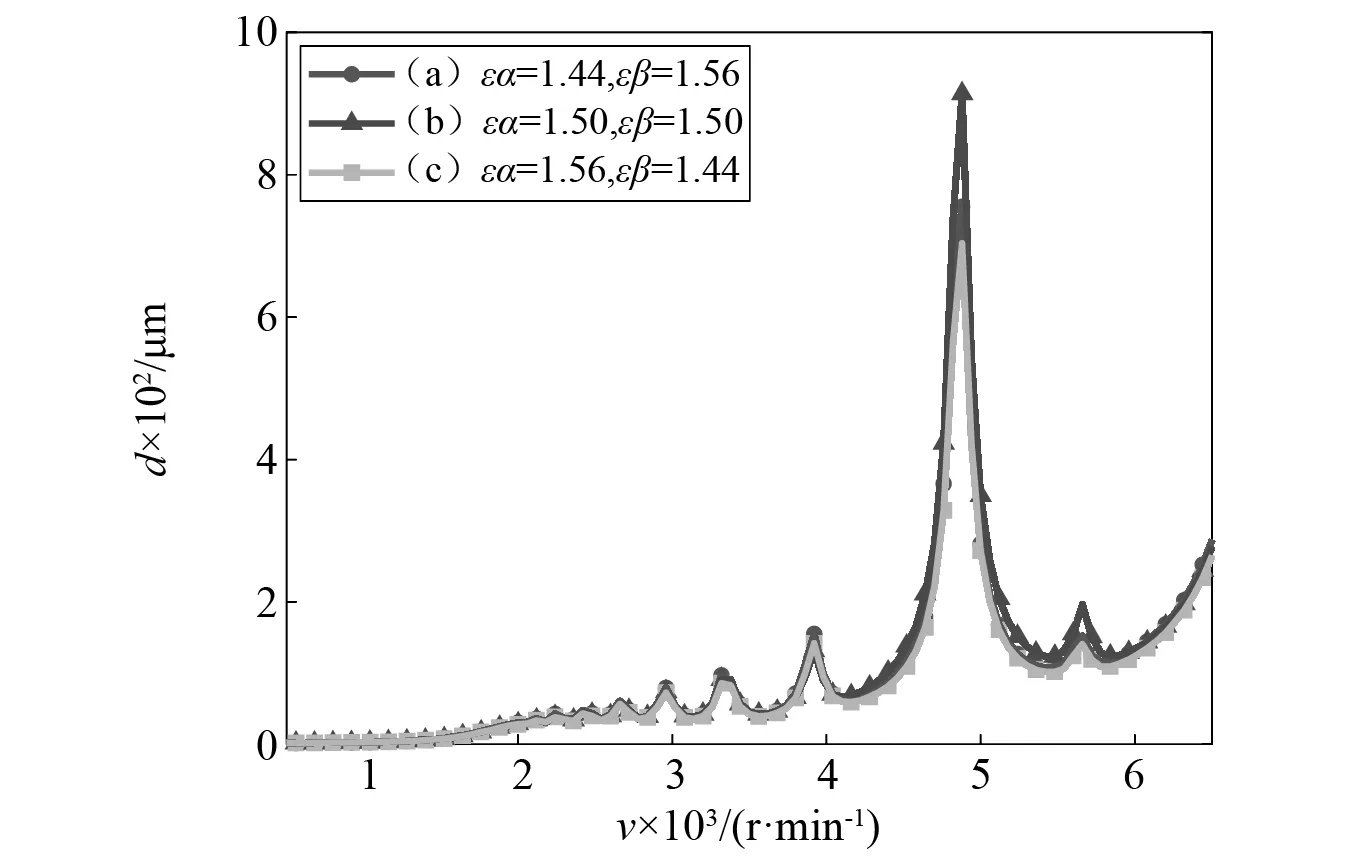
图12 三种不同重合度组合的速度-位移图Fig.12 Velocity-displacement diagram of three combinations with different coincidence degrees

进一步，固定输入转速为2 000 r/min进行频域分析，通过傅里叶变换，将三种不同重合度组合的振动位移时域信号转化为频域信号，结果如图13所示。可以看出，三种不同重合度组合除了在主频处存在振动幅值，还在2倍频、3倍频以及在1/2倍频处(仅(b)组合)存在较大的振动幅值。其中主频和2倍频处的振动幅值能量较大，特别在2倍频处(b)组合振动幅值较(a)和(c)组合凸出明显。(c)组合在1倍频和2倍频处的振动幅值较小，这与图5的时变啮合刚度变化规律相吻合。

图13 三种不同重合度组合的位移频域图Fig.13 Displacement frequency domain diagram of three combinations of different coincidence degrees

3 结 论

本文计入了箱体轴柔性、大重合度下斜齿轮时变啮合刚度影响，采用有限单元离散化建模方法，建立了某型6AT变速器主减齿轮系统的齿轮-轴-轴承全耦合动力学模型，通过数值算法对系统的固有特性与动态特性进行分析，得出以下结论：

(1)计入箱体轴柔性后系统的低阶固有频率略微降低，但系统增加了新的模态与振动形式。

(2)输入转速在500～6 500 r/min内，主减齿轮啮合频率的1倍频和2倍频处出现了明显的阶次幅值，随着倍次的增加，系振动能量变小，但当转速在4 900 r/min附近时系统出现明显的共振；而外界载荷的增大导致系统振动幅值的增加，但在共振点处主要受到固有频率下的模态振型影响。

(3)不同重合度比值影响系统时变啮合刚度的平均值与波动幅值，当端面重合度大于法向重合度时减弱了系统相对振动位移处幅值，在2倍频处体现的效果最为明显。