基于MTF-CNN的轴承故障诊断研究
赵志宏, 李春秀, 窦广鉴, 杨绍普
(1. 石家庄铁道大学 信息科学与技术学院,石家庄 050043; 2. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)
智能生产的发展加强了对早期故障诊断的需要,在机械设备中滚动轴承的运行状态往往直接影响机器能否正常工作。因此,精确的检测和诊断轴承的状态对于机械设备安全运行占有重要地位[1]。
一直以来,研究者提出多种故障诊断算法对轴承故障进行分类。Cai等[2]提出了能够进行诊断的面向对象贝叶斯网络复杂系统。Dong等[3]使用k-最近邻方法来完成轴承的故障诊断。Konar等[4]通过小波去噪对原始信号进行处理并提取特征,然后采用支持向量机进行轴承故障诊断。张钰等[5]从轴承振动信号中提取时域统计指标作为特征向量,然后利用随机森林进行诊断。这些方法不能直接从原始信号中提取特征,因此,研究直接从轴承振动信号中提取特征并自动识别轴承健康状态的诊断方法具有重要的研究价值。
近年来,深度学习(deep learning,DL)方法受到研究者的关注,DL方法克服了无法从大量数据中自动提取故障特征的难题,许多DL模型已被应用于故障诊断并取得良好的效果。曲建岭等[6]提出基于端到端的自适应一维卷积神经网络(convolutional neural network,CNN)模型来实现轴承故障诊断。赵敬娇等[7]提出一种基于双向长短期记忆网络(BiLSTM)的诊断模型,通过BiLSTM自动提取轴承原始振动信号特征,从而实现轴承故障诊断。张西宁等[8]提出一种具有复杂特征提取能力的深度卷积自编码器,以原信号和重构信号差值最小为目标,通过对卷积核优化和样本微调达到良好的故障诊断效果。
一维CNN在检测信号局部相关性存在不足,Wu等[9]通过卷积神经网络中一维信号输入与二维信号输入的分类性能进行对比,得到二维信号有更高的分类精度和鲁棒性。因此,将一维振动信号转换为二维图像进行轴承故障诊断得到研究者的重视。Wen等[10]提出将振动信号转换为二维灰度矩阵然后进行故障诊断。李恒等[11]将振动信号进行短时傅里叶变换得到时频谱,然后输入卷积神经网络进行故障诊断。袁建虎等[12]利用复Morlet小波将轴承振动信号转换为二维时频图像后进行故障诊断。上述方法忽略了振动信号不同时间间隔内信息的相关性,不能很好地体现信号之间的长期依赖关系。
马尔可夫变迁场(Markov transition field,MTF)利用马尔可夫转移概率来保留时域之间的信息关系[13]。首先,通过对振动信号的值域进行划分,并计算划分后值域之间的转移概率;然后,按照振动信号采样点的顺序,通过当前采样点所在值域和下一采样点所在值域之间的转移概率得到MTF矩阵,从而保留了振动信号的时间依赖关系和频率特征。基于此,本文提出一种基于MTF-CNN的轴承故障诊断方法,利用MTF对轴承振动信号进行编码生成二维图像,之后将其输入到CNN实现故障特征的提取,进而实现故障诊断,通过与其他几种关于振动信号编码方式的对比,本文模型可以更有效的提取轴承故障特征,得到更好的故障诊断效果。
1 MTF图像编码
MTF可将振动信号转换成二维图像,主要通过构造MTF矩阵来保留信号时域中的信息。其编码过程如下:
步骤1将轴承振动信号以N个采样点为一组进行划分;
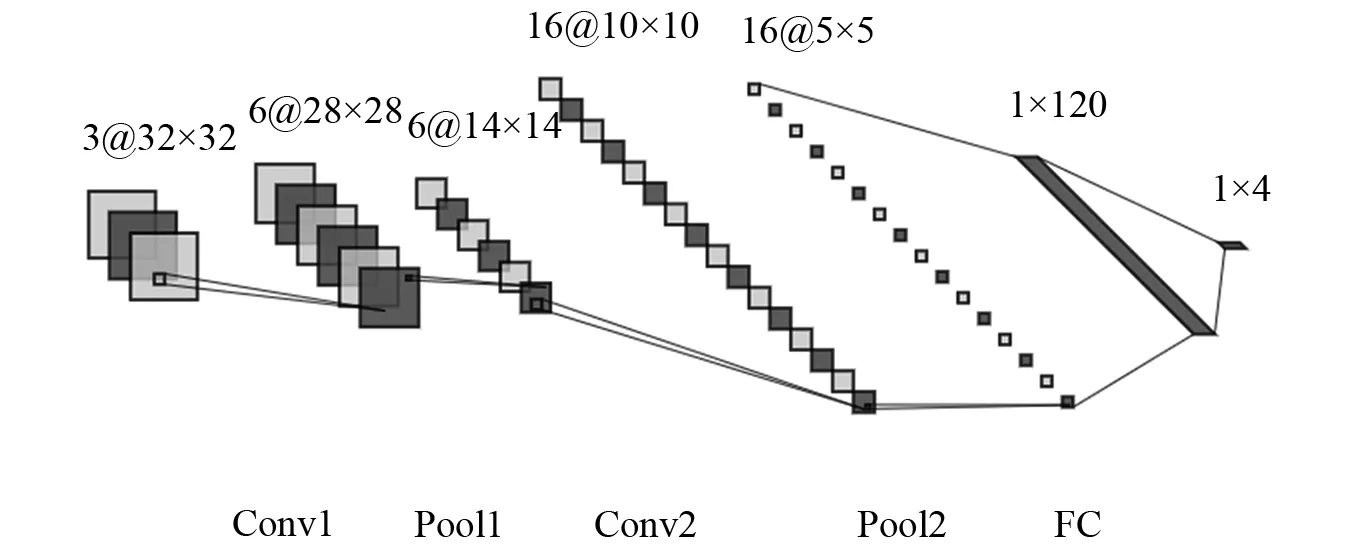
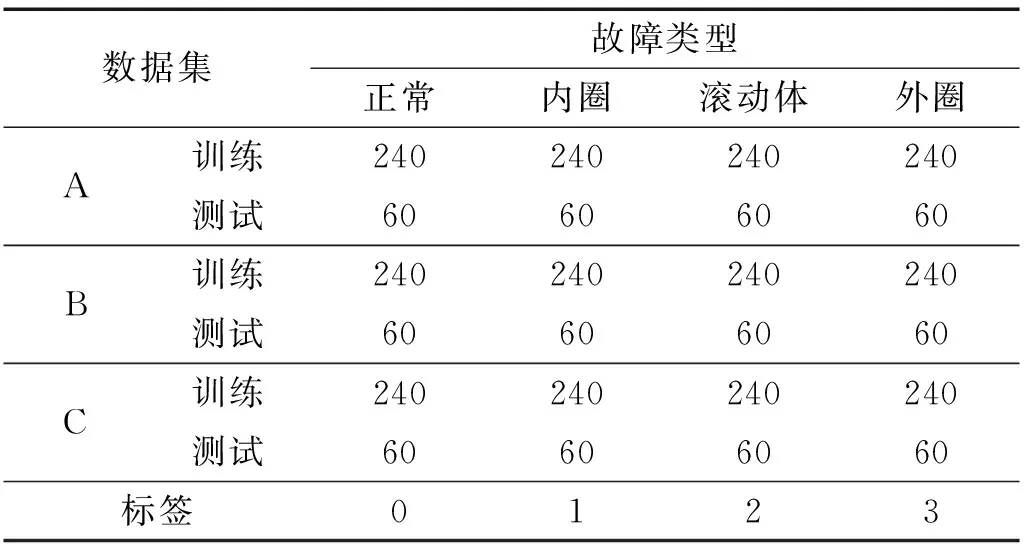
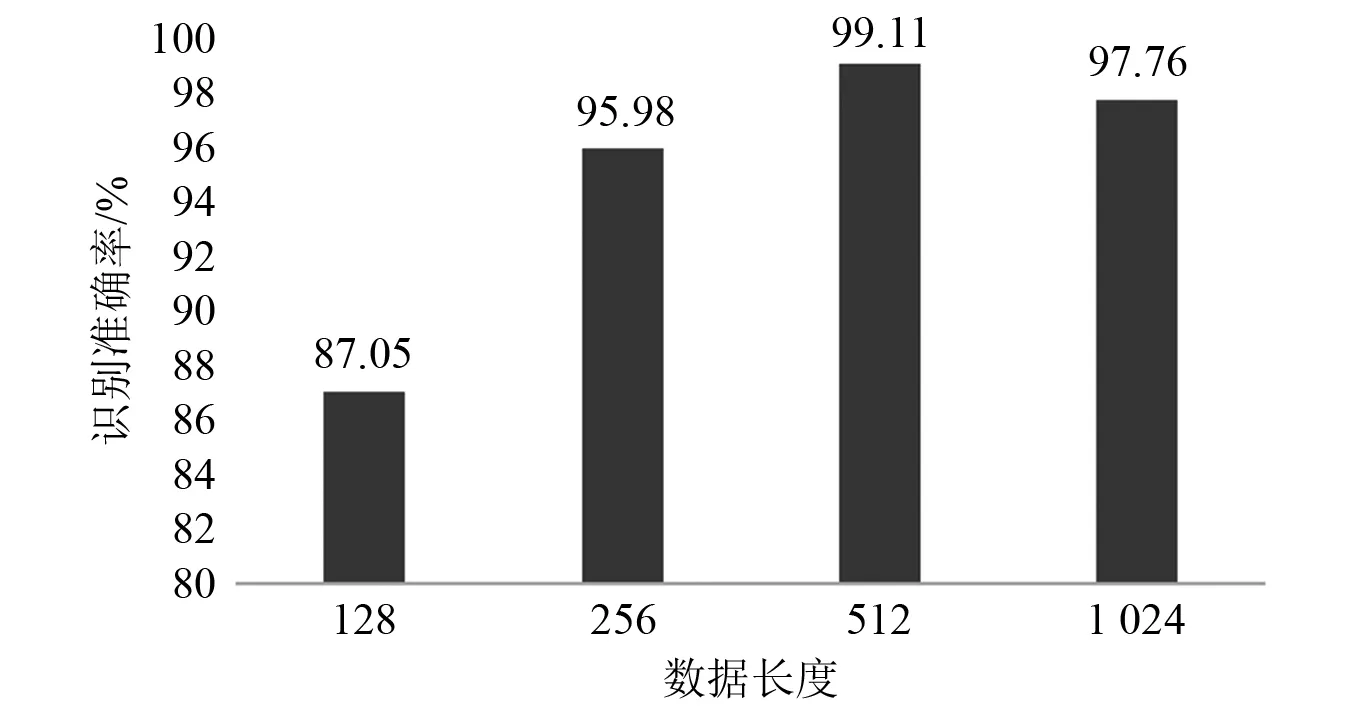
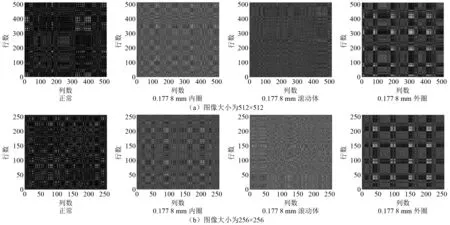
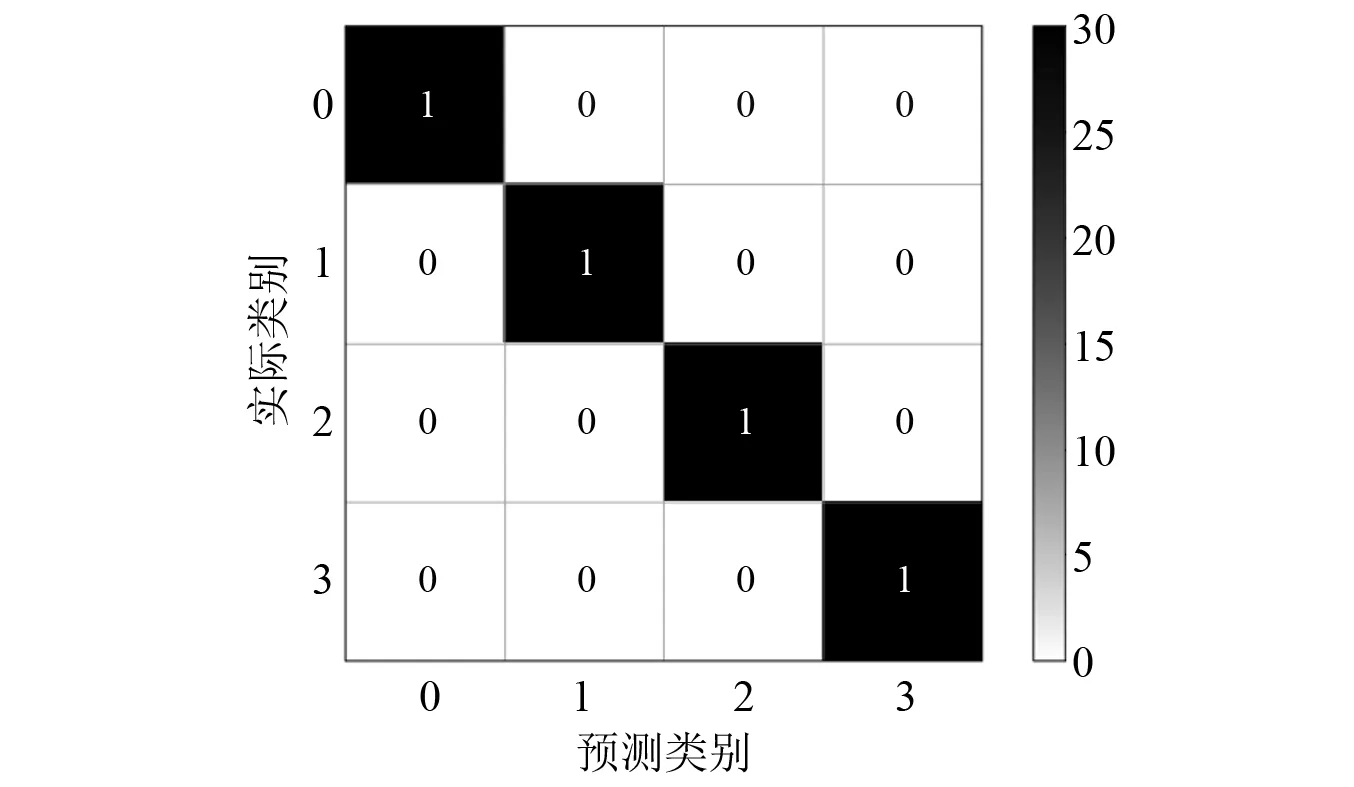
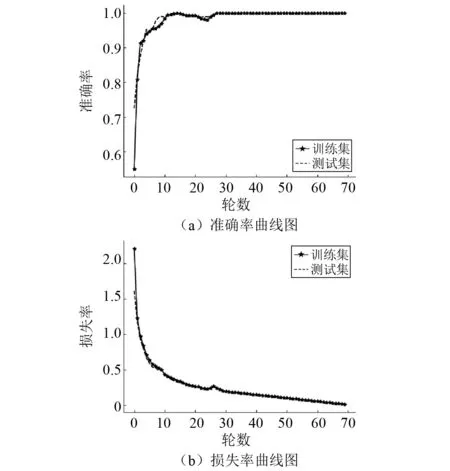
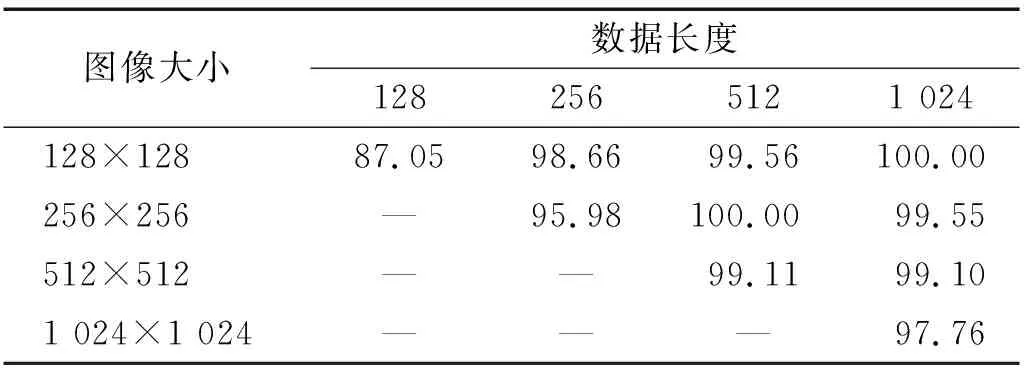
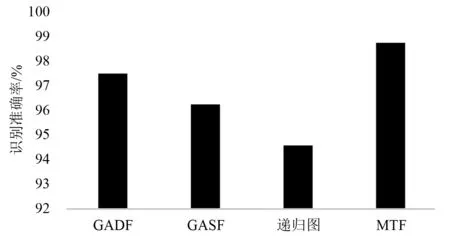
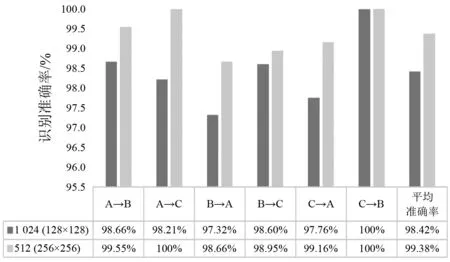
步骤2对划分的采样点进行序列标注,序列记为Xi(0 步骤3根据马尔可夫链原理[14]计算振动点所在的值域qj之间的转移概率,以此构造一个Q×Q加权邻接矩阵W,其元素Wij的值由值域qi中的所有振动点转移到值域qj中的概率给出 (1) 步骤4为了很好地显示时间序列特征,按照振动点的顺序来构建一个N×N的MTF矩阵,MTF中的mij表示xi所在的值域qi到xj所在的值域qj的转移概率。 (2) 为了使MTF编码图像更好地突出信息特征,采用像素平均法来改变图像的大小。将长度为64的轴承振动信号编码为不同图像大小的过程,如图1所示。由图1可知,采用像素平均法对图像进行压缩可以略去微小的信息差异,更好地突出数据之间的规律性。 图1 MTF编码图Fig.1 MTF coding diagram 卷积神经网络是DL的一个重要分支,CNN由具有可学习的权重和偏置常量的神经元组成,是一种前馈神经网络,它主要由卷积层、池化层和全连接层组成。Zhao等[15]提出了由一个卷积层和一个池化层组成局部特征学习块来收集输入数据的局部相关性。通过卷积层和池化层的叠加来提取输入数据特征并减少网络参数,提高网络性能。其中:卷积层通过卷积核按照指定的步长对输入的数据进行局部特征的提取;通过池化层对输入数据进行降维,减少网络参数量并降低复杂度,减少冗余特征[16]。 为了更好地比较MTF的性能 ,本文采用基本的CNN模型结构。具体的模型结构如图2所示,图2由Conv1、Pool1、Conv2、Pool2、FC1、FC2组成,利用全连接层进行分类,输入图像的大小为32×32,通道数为3,激活函数使用softmax函数[17],并使用交叉熵损失函数计算故障预测概率分布和真实故障概率分布之间的距离,具体的网络参数如表1所示。 图2 模型结构图Fig.2 Model structure diagram 表1 网络参数Tab.1 Network parameters 基于MTF编码方式和CNN网络的轴承故障诊断模型可直接从原始振动信号中提取特征。首先,进行振动信号MTF编码生成二维图像;然后,建立CNN模型,通过输入图像进行训练。基于MTF-CNN的轴承故障诊断方法的具体步骤为: 步骤1按照一定的数据长度对轴承振动信号进行划分,并划分训练数据集和测试数据集; 步骤2将划分好的数据按照MTF编码方式编码为二维图像; 步骤3将转换的图像作为特征图输入构建好的卷积网络模型中并对参数调优,使其能够提取故障特征信息; 步骤4通过Softmax分类器将其与故障类型建立映射关系实现故障诊断。 试验采用凯斯西储大学轴承数据集[18]对MTF-CNN模型进行验证,选取6205-2RS JEM SKF型号的DE驱动端轴承数据,采样频率是12 kHz,故障直径为0.177 8 mm,故障类型包括内圈故障、滚动体故障以及外圈故障,试验数据样本构造如表2所示,其中数据集A是转速为1 797 r/min的4类轴承数据,数据集B是转速为1 772 r/min的4类轴承数据,数据集C是转速为1 750 r/min的4类轴承数据。 表2 轴承数据集Tab.2 Bearing dataset 对数据进行MTF编码前需要将振动信号按一定的长度进行划分,MTF编码图的矩阵行数和列数的选择依据是:一方面可以充分提取振动信号中的特征信息;另一方面便于后续处理,MTF编码过程中使用步长为2的像素平均法,因此行数和列数选取2的幂次大小。综合考虑之后,本文矩阵行数和列数的大小设置为512。在试验中,每一类故障构造300个样本,按照8∶2的比例进行训练集和测试集划分,划分后分别为不同轴承故障类型标签进行One-hot 编码[19]。 根据MTF编码原理可知,数据长度的选取对编码图像有一定的影响,这里研究不同数据长度对故障识别率的影响。试验数据采用表2的数据集A,按照128,256,512和1 024不同的长度对轴承信号进行MTF编码,然后采用CNN进行故障诊断。设置学习率为0.001,试验结果如图3所示。由图3可知:当数据长度为128时,故障诊断准确率较低,这是因为振动信号采样点太少,不能很好地反映故障特征;随着数据长度的增加,模型的诊断准确率上升,当数据长度为512时,故障诊断准确率最高,达到99.11%;当数据长度增加到1 024时,模型的准确率又有所降低,这是因为MTF编码是以振动信号数值划分的值域之间的转移概率来进行编码。所以当数据长度过大时,转移概率值的相似度会越来越高,降低了不同特征数据之间的区分性。试验结果表明,在不采用像素平均法改变MTF矩阵大小的前提下,数据长度为512的MTF编码效果最好。 图3 不同数据长度对故障识别率的影响Fig.3 Influence of different data length on fault recognition rate 当数据长度为512时,生成的MTF图像大小为512×512,使用像素平均法将图像缩小为256×256,2种不同大小的图像如图4所示,以故障直径为0.177 8 mm的3种故障类型和正常信号为例,图4(a)所示图像大小为512×512,图4(b)所示图像大小为256×256,从 图4中可知,两组图像的4种特征都比较明显,但是图4(b)中4种类型之间的差异性更大,更容易进行轴承类别区分。对比图4(a)与图4(b)可以看出,经过像素平均值改变图像大小后,其故障特征规律性更明显。 图4 数据长度512的MTF轴承编码图Fig.4 MTF bearing coding diagram with data length 512 对图像大小为256×256的数据集进行故障诊断试验,得到的分类混淆矩阵如图5所示。图5中:0~3分别表示轴承的4种类别;对角线上深色区域数值是每类故障的准确率;其余部分的数值为误分类率。从图5可知,每一类故障识别准确率都达到100%。 图5 分类混淆矩阵Fig.5 Classification confusion matrix 进一步分析卷积神经网络对MTF编码图的特征提取与故障识别能力,模型训练过程中的准确率和损失率曲线,如图6所示。从图6中可知,收敛速度很快,30代之后便趋于稳定状态。训练集和测试集的准确率都达到100%,损失率呈下降趋势直至趋于0,模型学习效果比较好。 图6 数据长度为512模型准确率及损失率曲线Fig.6 Accuracy and loss rate curve with data length of 512 进一步研究图像大小对模型准确率的影响,对128,256,512和1 024等4种不同的数据长度进行试验研究,试验结果如表3所示。由表3可知,采用像素平均法压缩图像的大小后,模型的诊断准确率均得到提升。当数据长度为1 024时,生成的MTF图像大小为1 024×1 024,模型的准确率为97.76%;采用像素平均后,图像大小为512×512,模型的准确率提高到99.1%;再次采用像素平均进行图像压缩,图像大小为256×256,模型准确率得到99.55%;进一步像素平均后,图像大小为128×128,此时模型的诊断准确率为100%。试验结果表明,MTF编码图经过像素平均压缩图像大小后可以得到更好的故障诊断效果。其中数据长度为512,图像大小为256×256和数据长度为1 024,图像大小为128×128得到的故障诊断正确率最好。 表3 不同图像大小的模型准确率Tab.3 Model accuracy of different image sizes 单位:% 为了进一步验证轴承振动信号MTF编码的模型诊断效果,与其他振动信号图像编码方式进行比较试验。轴承振动信号编码为二维图像的方式主要有格拉姆角场(GAF)和递归图,其中格拉姆角场包括格拉姆角和场(GASF)和格拉姆角差场(GADF)2种。文献[20]的研究结果表明,数据长度为300的GADF编码效果最好。为了便于比较,同样设置长度为300对轴承数据进行划分,之后将不同方式编码后的图像作为特征图输入卷积神经网络进行特征提取与分类,得到的试验结果如图7所示。由图7可知,MTF编码的故障识别效果最好,GADF编码方式也得到较高的故障诊断率,递归图效果相对较差。试验结果表明,与其他编码方式相比MTF具有更好的轴承故障特征提取能力。 图7 不同图像编码方式对比Fig.7 Comparison of different image coding methods 为了验证该模型在不同载荷条件下的诊断效果,将表1中不同的数据集分别作训练集和测试集来对模型的泛化能力进行验证,试验A→B代表在A数据集上进行训练,B数据集上进行测试。分别对数据长度1 024图像大小为128和数据长度512图像大小为256这两组图像数据进行泛化试验,试验结果如图8所示。由图8可知,两组试验都取得了较高的准确率,诊断识别率都达到了98%以上,表明本文模型有较好的泛化能力。 图8 载荷改变时故障识别率Fig.8 Fault recognition accuracy when the load changes 本文提出一种基于MTF-CNN的轴承故障诊断方法并进行了试验研究,从中可以得到以下结论: (1) 正常轴承、内圈故障、外圈故障、滚动体故障的MTF编码有明显不同,从轴承振动信号的MTF编码图像中可以有效提取故障特征信息。 (2) MTF编码图的数据长度和图像大小对轴承故障诊断效果影响比较大,需要根据应用的不同场合确定合适的数据长度和图像大小。 (3) 通过与其他编码方式进行比较试验,结果表明,MTF编码方式在轴承故障诊断中的准确率高于GAF和递归图编码方式。 (4) 为了验证模型的泛化性能,选用不同载荷的数据作为训练集和测试集进行试验。结果表明,该模型在载荷发生改变时,依旧取得了较高的试验准确率,具有较好的泛化能力。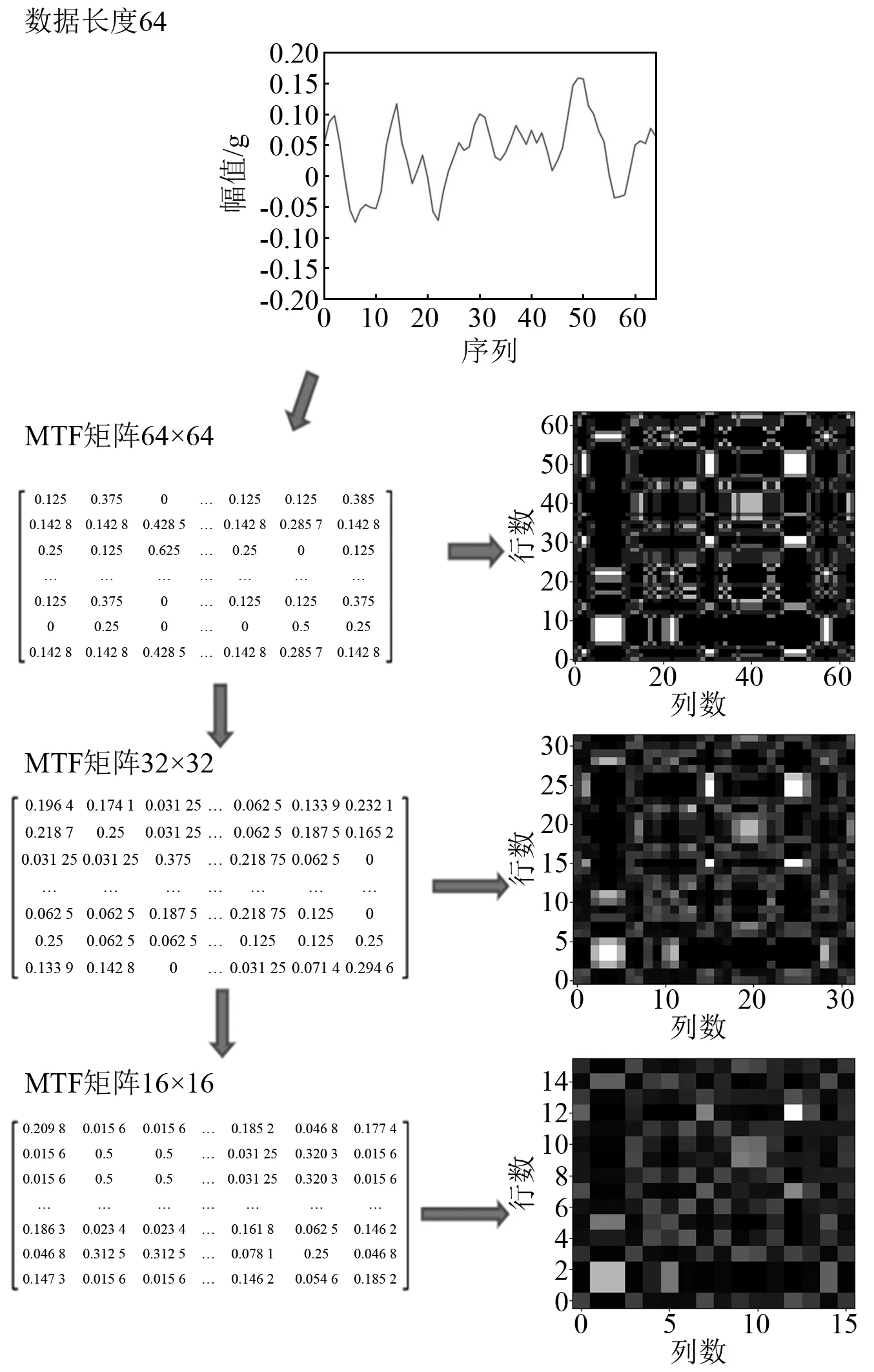
2 模型结构

3 MTF-CNN滚动轴承故障诊断方法
4 试验研究与分析
4.1 试验数据
4.2 试验结果与分析
4.3 不同图像编码方法比较
4.4 泛化试验
5 结 论

