包装件在非高斯随机载荷下响应特征分析方法研究

朱大鹏， 王浩然， 曹兴潇

(1. 兰州交通大学 交通运输学院，兰州 730070； 2. 兰州交通大学 机电工程学院，兰州 730070)

包装件在流通过程中，在车辆运输环节，长时间受到随机振动载荷作用。包装件在随机振动载荷激励下，内装的产品或产品的关键部件可能会发生首次穿越破坏或者疲劳损伤。为提高包装件在随机振动载荷条件下的可靠性，近年来，国内外研究者围绕随机振动环境模拟、包装件响应分析等，开展了大量研究工作。Lepine等[1]介绍了目前公路运输中车辆随机振动载荷的模拟和包装件振动测试方法，包括非高斯和非平稳随机振动模拟方法。曾昕等[2]基于运行测试方法，提出一种非平稳指数的表征方法，基于峭度和功率谱密度函数等约束条件，利用贝塔分布随机数模拟生成非平稳非高斯随机振动。Lamb等[3]根据采集的公路运输条件下车辆内的振动数据，分析了道路类型、车辆悬挂参数等对车辆随机振动的影响。Hosoyama等[4]考虑了随机振动的非高斯特性，将包装件建模为单自由度振动系统，研究包装件动态特性对响应峭度的影响，为优化包装设计提供了理论依据。Wang等[5]考虑到包装件的复杂性，基于包装件中元件线性振动假设，提出了运输包装件加速振动测试方法。王志伟等[6]研究了不同包装件约束、不同振动等级条件下，不同谱型的随机振动激励对包装件加速度响应和动压力的影响。文献[7]分析了随机振动载荷下，无约束包装件的跳动对包装件加速度响应非高斯特性的影响。于水源等[8]采用数值模拟方法对包装件疲劳特性进行了分析。

将包装件建模为振动系统，分析包装件在随机振动条件下的响应特征是分析包装件振动可靠性或疲劳特性的重要基础，也是对包装件进行优化的重要前提。如果随机振动激励是平稳高斯的，对于线性包装件，可采用分析法得到包装件的响应。对于非线性包装件，目前可采用FPK(fokker-planck-kolmogorov)法、摄动法、随机平均法、等效线性化法等分析其随机响应。由于道路不平[9]、包装件在运输过程发生跳动、车辆悬挂特性具有时变性[10]等原因，包装件在运输过程中经常受到非高斯随机振动激励。近年来，非高斯随机振动的模拟及非高斯随机振动条件下包装件的响应分析已成为运输包装领域的研究热点。蒋瑜等[11-12]基于非高斯随机振动的PSD，提出了一种新的基于幅值调制和相位重构的算法，生成不同偏斜度和峭度的非高斯随机振动。Grigoriu[13-14]采用非线性零记忆变换的方法，对高斯分布的随机振动进行单调变换，实现非高斯随机振动的模拟。杨喆等[15]结合多项式混沌展开方法和Karhunen-Loeve展开，用标准正态随机过程的非线性函数表达非高斯随机过程。

在非高斯随机振动载荷激励下，包装件的响应分析较为困难，即使对于线性振动系统，分析其响应的计算量也较大[16]。对于非线性包装件，很难采用分析法直接获得其响应的统计特征参数，目前主要通过蒙特卡洛模拟法分析包装件的响应统计参数，根据这些统计参数再现包装件的随机响应。由于传统蒙特卡洛法计算量很大，可采用拟蒙特卡洛分析法[17]，通过合理的随机变量采样策略，提高传统蒙特卡洛法的分析效率，提高响应统计参数的收敛速度。虽然采用拟蒙特卡洛法可改进蒙特卡洛分析的效率，但该方法与分析法相比还存在着计算量大、分析效率低的缺点。

本文提出非高斯随机振动载荷条件下，非线性包装件的加速度响应统计特征分析方法。首先，本文采用非高斯Karhunen-Loeve展开法[18-20]模拟非高斯随机振动载荷，将非高斯随机振动载荷表达为非高斯随机变量的线性组合。对非线性包装件的响应进行一阶泰勒展开，根据该展开式，分析响应的各阶矩统计参数和自相关函数，采用鞍点估计法分析包装件加速度响应的概率密度函数(probability density function,PDF)和累积分布函数(cumulative distribution function,CDF)，从而可分析包装件的振动可靠性、疲劳特性等。由于本文方法中，非高斯随机振动表示为非高斯随机变量的线性组合，以该非高斯随机振动的模拟方法为基础，对非线性包装件的响应进行的线性化处理(一阶泰勒展开)具有误差小的特点，这与文献[21]提出的非线性包装件等效线性化处理方法在本质上是一致的。因此，本文的方法与传统的基于蒙特卡洛模拟方法相比，具有分析效率高、精度好的优点。

1 非高斯随机振动的模拟算法

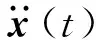
(1)

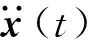
(2)

向量ξi满足

E[ξi]=0

(3a)

E[ξiξj]=δij

(3b)

式中，δij为Kronecker-Delta函数。

实际应用中，通常在式(1)中采用有限项表示随机过程，式(1)可简化为[22]

(4)

对于呈高斯分布的随机振动，采用Karhunen-Loeve展开表示该随机振动时，在式(4)中，ξi为标准正态随机变量，且满足式(3a)和式(3b)。对于非高斯随机振动，则需要对式(4)中的ξi分析，通过合理选择随机变量ξi的概率密度函数，实现非高斯随机振动的数值模拟。确定ξi的算法如下：

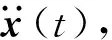
(5)

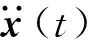
(6)

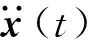
步骤2根据累积分布函数F，生成M组随机向量ξi(θm),i=1,2,…,M,m=1,…,N，对其进行标准化处理，使其均值和方差分别为0和1，且满足式(3a)和式(3b)，将这N组随机向量ξi(θm)代入式(4)中生成N个非高斯随机振动样本

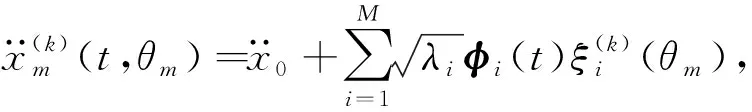
(7)

式中：k为迭代次数；m为模拟的非高斯随机振动样本编号

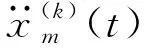
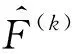
(8)

步骤5用式(9)对ξi进行更新迭代

(9)

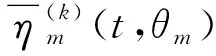
步骤6重复步骤2～步骤5，直至模拟的非高斯随机振动累积分布函数与目标累积分布函数误差小于给定的阈值，或相邻迭代步骤中误差变化很小。

在以上算法步骤中，不仅需要保证模拟的非高斯随机振动累积分布函数和目标累积分布函数一致，还需要保证在迭代过程中，模拟的非高斯随机振动的自相关函数与目标自相关函数C(τ)一致。为达到该目标，在每次迭代中，计算出的Karhunen-Loeve展开式中的随机变量ξi(θm)(i=1,2,…,M,m=1,…,N)应满足式(3a)和式(3b)，以确保在迭代过程中模拟的非高斯随机振动的自相关函数C(τ)保持不变。本文采用优化拉丁超立方采样法[24]，在不改变随机变量ξi(θm)(i=1,2,…,M,m=1,…,N)的累积分布的基础上，调整随机变量ξi的分布位置，减小随机变量之间相关性，使其满足式(3a)和式(3b)。首先建立一个N×M矩阵X，在该矩阵中放置生成N个非高斯随机振动随机变量ξi(θm)，该矩阵的每列随机变量符合累积分布函数F，对每列随机变量，根据其大小排序编号，与矩阵X对应，我们构建一个N×M矩阵R，该矩阵中各元素为矩阵X中各元素的排序编号，即矩阵R各列为1～N的正整数。矩阵R第i列和第j列之间的相关性可由M×M矩阵T定义，该矩阵中的元素Tij为Spearman排序相关系数，由式(10)定义[25]

(10)

由于T是一个正定矩阵，对T进行Cholesky分解运算

T=Q′Q

(11)

式中，Q′为矩阵Q的转置。对初始的包含随机变量排列位置的矩阵R进行变换

R′=RQ-1

(12)

根据矩阵R′每列中包含的随机变量排列位置，调整随机变量ξi的位置，可大大降低随机变量ξi之间的相关性。

对随机变量ξi位置调整后，还需对其标准化，代入Karhunen-Loeve展开式中，式(7)改写为

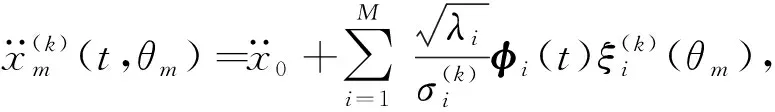
(13)

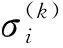
以上方法在随机变量ξi的分布不变的条件下，调整了其位置，并对其标准化处理，其目的在于令随机变量ξi满足式(3a)和式(3b)。根据Phoon等的推导，满足式(3a)和式(3b)的随机变量ξi代入式(7)中，模拟的非高斯随机振动信号的自相关函数与目标自相关函数保持一致。因此，在每次迭代中，模拟的随机振动的自相关函数保持不变，且与目标自相关函数保持一致，确保了模拟的振动信号频域特性准确性。

2 包装件振动响应模拟

将包装件中的产品看作是一个刚性质量块，将包装件建模为支座激励单自由度振动系统，如图1所示，其运动方程式为

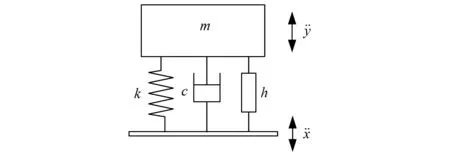
图1 单自由度包装件模型Fig.1 Single degree of freedom package model

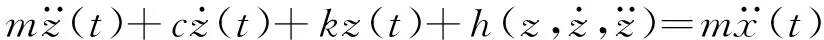
(14)

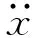
(15)

式中，μξi为ξi的均值。为计算式(14)中的偏微分项，对式(14)中的各项对随机变量ξi求偏微分

(16)

式中，缓冲材料非线性项对随机变量ξi的偏微分为

(17)

结合式(16)和式(17)，得

(18)

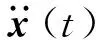
(19)

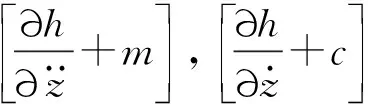
(20)

根据式(15)，包装件加速度响应的均值为

(21)

式中， E[·]为期望值运算，由于在式(21)中

故包装件响应的均值为

(22)

式中：μξ=[μξ1,μξ2,…,μξM]；μξi为ξi的均值，根据式(15)和式(22)，有

(23)

对式(23)的平方求期望值，可得

(24)

由于随机变量ξi,(i=1,…,M)的方差为1，且各随机变量之间不相关，故式(24)中，E[(ξi-μξi)2]=1，且当i≠j时，E[(ξi-μξi)(ξj-μξj)]=0，故根据式(24)可得包装件响应的方差表达式

(25)

同理，可得包装件加速度响应的三阶统计矩和四阶统计矩的表达式

(26)

(27)

包装件加速度响应的自相关函数为

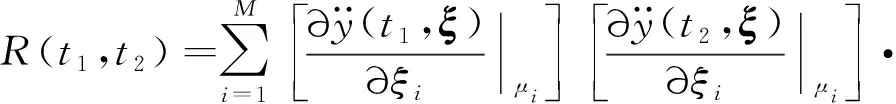
(28)

对于平稳非高斯随机振动，式(28)可简化为单参数函数

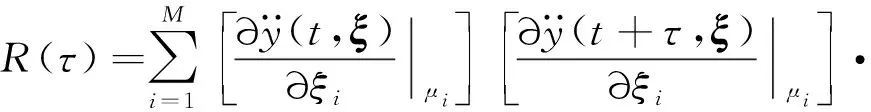
(29)

式中，τ=t2-t1。

3 振动响应统计特征分析

根据式(22)、式(25)～式(27)可得包装系统加速度响应的统计特征值，2020年朱大鹏根据这些统计特征值，结合多项式混沌展开和Karhunen-Loeve展开，模拟加速度响应的时域信号，采用拟蒙特卡洛法分析系统的振动可靠性。该方法虽然可以准确分析出系统可靠性，但计算量大，不适用于复杂系统的可靠性分析，不适用于需要多次分析可靠性的系统优化场合。鞍点估计法[26-27]是分析振动系统可靠性的一种高效准确分析法，在已知式(15)中随机变量ξi的PDF条件下，鞍点估计可准确估计出包装系统加速度响应的CDF，从而提供了一种分析响应可靠性的高效方法。但该方法需分析ξi的累积母函数，在式(15)中，ξi经过多次迭代优化后其PDF无法用分析式准确表达，或ξi的累积母函数非常复杂，导致鞍点估计计算量很大，这些因素都限制了鞍点估计法的应用。本文采用基于四阶统计矩参数的鞍点估计法[28-29]分析包装系统的可靠性，避免了分析ξi的累积母函数，具有良好的分析效率和通用性。

(30)

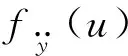
(31)

根据式(30)的定义，可得

(32)

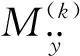
(33a)

(33b)

(33c)

(33d)

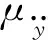
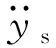
(34)

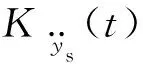
(35)

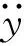
(36)

(37)

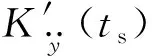
(38)

式中：Φ和φ分别为标准正态分布的累积分布函数和概率密度函数；参数w和v由式(39a)和式(39b)确定

(39a)

(39b)

式中，sgn(ts)=1,0,-1，对应的ts分别大于、等于、小于0。

根据式(36)和式(38)，可得包装件响应的PDF和CDF，可高效确定包装件响应的统计特征，包装件的振动可靠性可由响应的CDF确定。

4 实例分析

本部分采用实例介绍非高斯随机振动模拟、非线性包装件振动响应分析方法、振动可靠性分析方法。

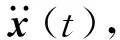
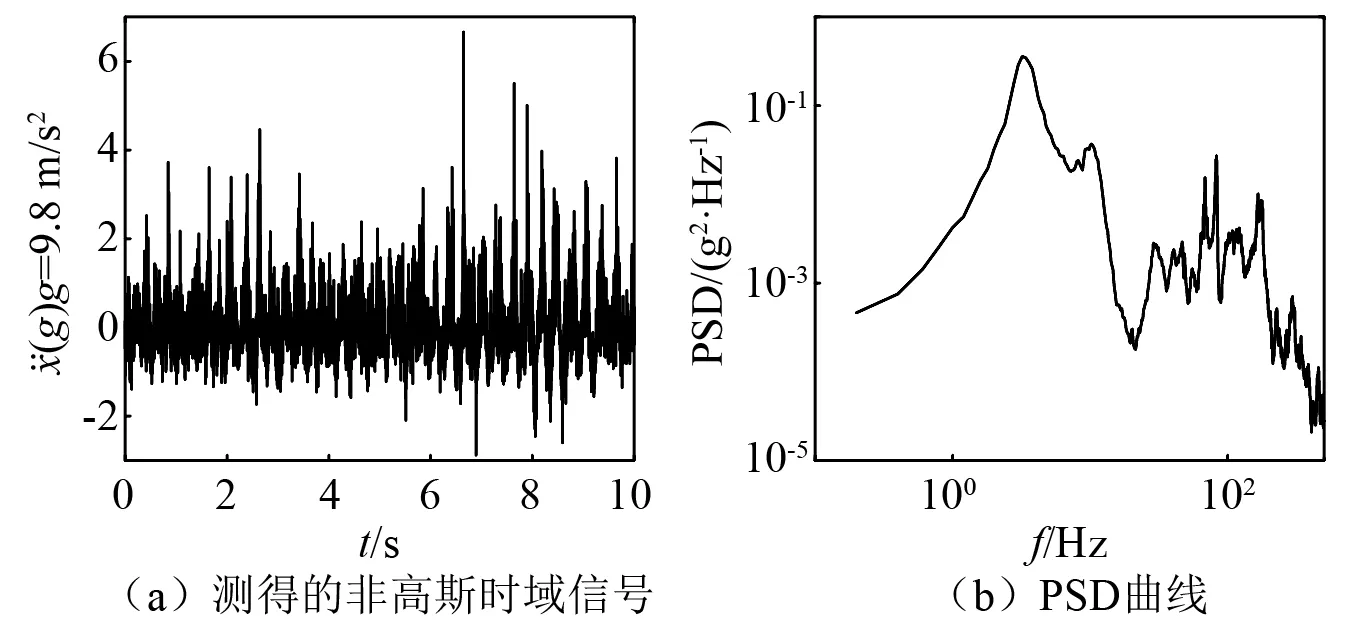
图2 试验记录的非高斯振动的时域信号和PSD曲线Fig.2 Recorded field non-Gaussian vibration time domain data and PSD curve

(40)

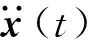
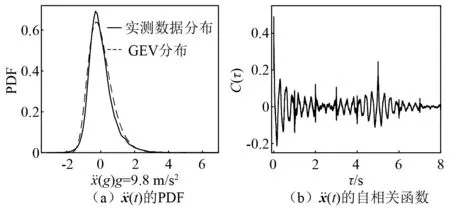
图3 的PDF和自相关函数Fig.3 PDF and autocorrelation function of

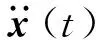
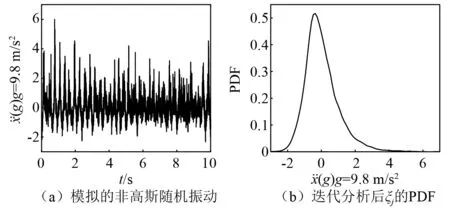
图4 模拟的非高斯随机振动的时域信号和迭代后ξi的PDFFig.4 Simulated time domain non-Gaussian random vibration and PDF of ξi after iterations

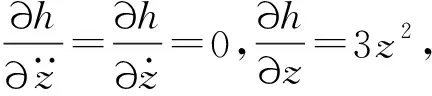
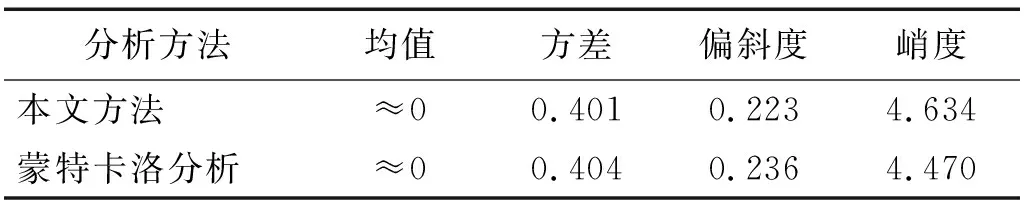
表1 包装件加速度响应统计参数Tab.1 Statistical parameters of package acceleration response

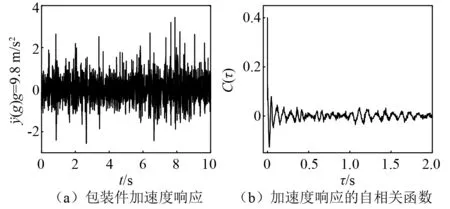
图5 包装件加速度响应的时域信号和自相关函数Fig.5 Time domain package acceleration response and the autocorrelation function

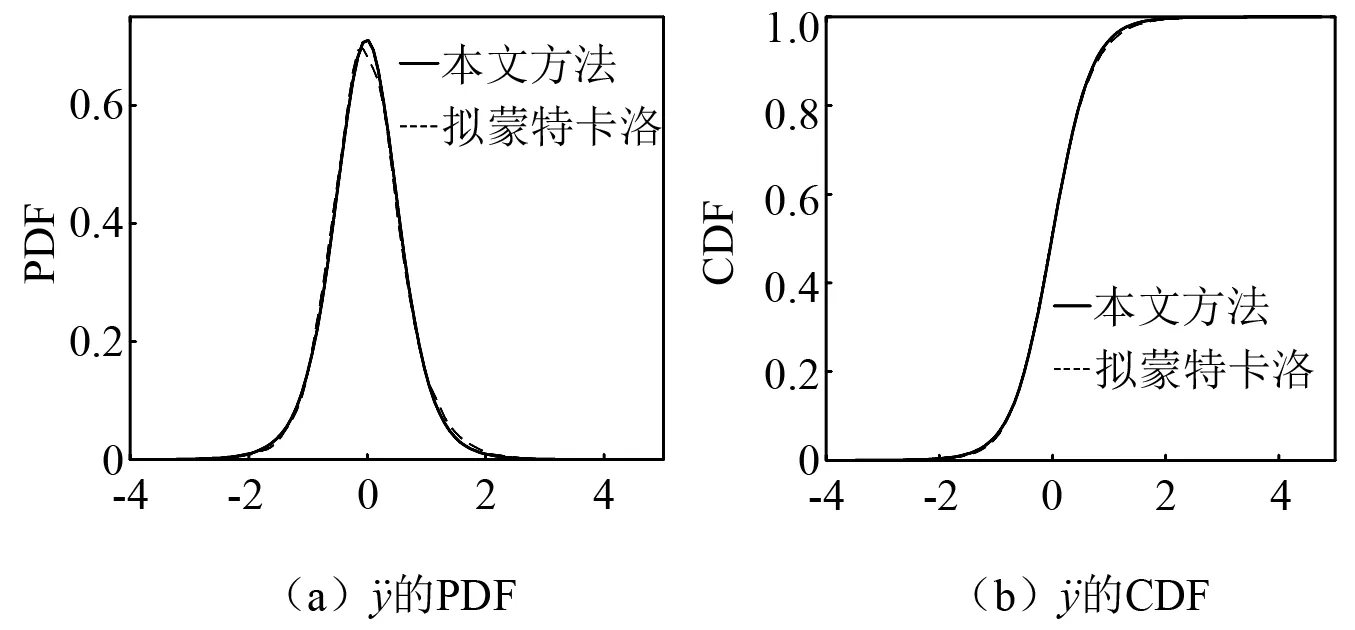
图6 的PDF和CDFFig.6 Analytical PDF and CDF of

5 结 论

本文提出一种平稳非高斯随机振动载荷下包装件加速度响应统计特征的高效分析方法，与传统的基于蒙特卡洛和拟蒙特卡洛分析法相比，本文的方法具有计算效率高、精度好的优点，特别适用于需要进行重复的包装件加速度响应统计特征分析和可靠性分析的包装系统优化、包装件参数优化的场合。论文主要成果如下：

(1) 为确保分析精度，本文将非高斯随机振动激励表示为非高斯随机变量的线性组合，在随机变量均值处对包装件加速度响应进行一阶泰勒展开估计，由于未对随机变量进行非线性变换，故采用一阶泰勒展开估计的误差较小，可确保本文方法的准确性。

(2) 本文提出了确定包装件加速度响应统计特征的分析方法，与蒙特卡洛和拟蒙特卡洛方法相比，具有快速高效的优点。

(3) 确定包装件响应加速度统计特征需要大量的加速度响应时域样本，因此需要大量的蒙特卡洛或拟蒙特卡洛分析，造成模拟计算量大、计算效率低，本文依据包装件加速度响应的前四阶统计矩，采用鞍点估计法，可高效准确得到包装件加速度响应的PDF和CDF，避免了蒙特卡洛或拟蒙特卡洛分析。

(4) 本文将复杂包装件简化为单自由度振动系统进行分析，本文基于该简化模型提出了包装件振动响应统计特征分析方法，包装件的简化模型的准确性对于分析包装件在运输过程中的响应、评价包装件可靠性、对包装件进行优化设计等至关重要。因此，需建立包装件等效简化模型分析方法，根据包装件振动实验数据识别包装件简化模型弹性特性和阻尼特性的类型，并识别具体的模型参数。该工作是今后本领域的一个重要研究方向。