加速环境下基于终身保修的最优预烧时间

王洪庆，王亚男，宋云涛

(中国消防救援学院，北京 102202)

众所周知，在当今竞争日益激烈的市场中，产品的保修政策对于产品的销售起着至关重要的作用。为了保护消费者的权益，以及引起他们购买产品的兴趣，耐用的产品在销售的时候都会采用一定的保修政策。从消费者的角度来讲，当然希望产品有较长的保修期。但是对于生产商来说，更长的保修期通常会伴随着更大的保修费用的支出，这样保修的费用在产品的完整生产、销售过程成本中占有相当大的比重，所以如果产品在整个生命周期的早期具有较高的产品可靠度将会显著的减少生产商的保修支出。

随着产品市场的不断发展，生产商已经开始提供长期的保修政策，并且保修期越来越长，具体的例子可以参考文献[1-3]。事实上，在现在的商品市场中，许多生产商已经开始提供终身保修政策。例如，安装在汽车电路系统上的继电器的保修期，抽油烟机的过滤网的保修期等都是终身保修的，此处的“终身”指的就是汽车和抽油烟机的寿命，容易看出这个保修期是一个随机变量。

G.Chattopadhyay和A.Rahman[1]定义了终身保修，生产商承诺如果售出的产品在使用期间由于设计缺陷或者制造缺陷等原因产生故障，那么生产商将提供免费或者分摊费用的维修或者更换服务。

1 保修策略

在本文中，我们研究与G.Chattopadhyay和A.Rahman[1]中不同的两种典型终身保修策略。

保修策略①(终身免费保修)在此策略下，对于所有因为生产控制或者设计等原因造成的产品缺陷以及故障，生产商要承担完全责任。如果可以修理就进行修理，不能修理直接更换。

保修策略②(单次保修费用有上限的终身保修)在此策略下，如果每次保修的花费不超过约定的费用上限，那么费用由生产商全部承担；如果超过约定的费用上限，则由生产商承担费用上限，超出的部分由消费者承担。

以上两种策略中的保修期与通常的保修期不同，终身保修的保修期是一个不确定的随机变量。这两种保修策略是非常有代表性的，在工业设备以及各种家用电器的生产销售中有着广泛的应用。

由于产品越早失效将会导致越高的保修费用，所以经常采用预烧的办法来避免产品在实际应用阶段初期失效。也就是说，产品在生产出来之后，销售之前在与现实工作近似相同的条件下模拟工作一段时间，在这段时间内失效的产品将不会被出售。预烧测试起源1940年代晶体管被发明出来，关于预烧知识的介绍可参见文献[4-8]，Cha[8]和Finkelstein[9]分别给出了新的预烧策略。由于预烧时间过长会对产品产生损害，过短起不到应有的作用，因此需要确定预烧测试所应持续的时间，即最佳预烧时间。Nguyen和Murthy[10]在20世纪80年代首先提出运用模型来确定带有保修期的产品的最佳预烧时间，Mi[7]和Chou、Tang[11]在此模型基础上进行了进一步的研究。

现在，由于科技进步和生产水平的提高，许多产品都具有较高的可靠度，其潜在的缺陷需要较长的时间来进行探测。为了节省预烧时间，Block和Savits[4]提出了在加速环境下进行预烧的方法。Cha[12]在加速环境下提出了一个新的失效率模型。

Block、Savits和Singh[13]指出，大量的实验数据表明许多产品，特别是电子产品的失效率函数具有浴盆形状。即失效率函数最初递减，随后的一段时间里保持不变，后期由于老化、磨损等原因而递增。

定义1[13]一个失效率函数r(t)称为浴盆形失效率函数，如果存在着0≤t1≤t2≤∞， 使得

此处t1，t2称为r(t)的变点。区间[0,t1)称为早期失效期；区间[t1,t2]称为正常工作期，在此区间内r(t)达到最小值而且保持不变，所以也称为平稳失效期；区间(t2,∞]称为耗损失效期。

浴盆形失效率函数的图像参看图1。

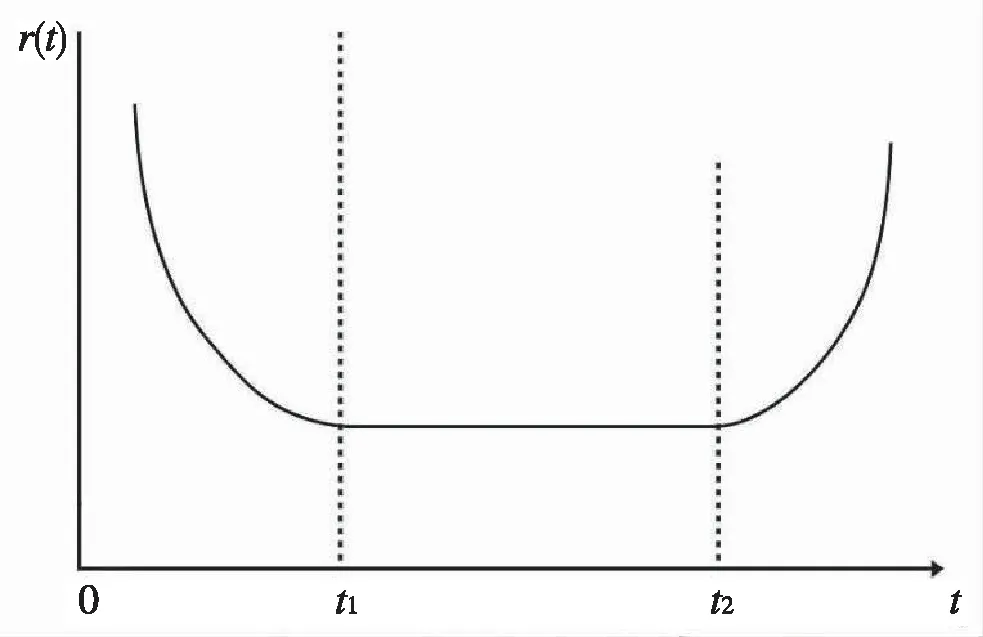
图1 浴盆型失效率函数

本文第2节介绍了所要使用的一些记号以及相关的假设,第3节描述了加速环境下的失效率模型,第4节通过4个定理给出了本文的重要结果,最后在第5节进行了简要的总结。

2 记号及假设

2.1 记号

X，XA—非负、连续的随机变量，分别用来表示产品在正常工作环境、加速工作环境下的寿命；

F(t)，FA(t)—X，XA的累积分布函数；

f(t)—X的密度函数；

r(t)，rA(t)—X，XA的失效率函数；

T—保修策略1及保修策略2中的“寿命”；

b—预烧时间；

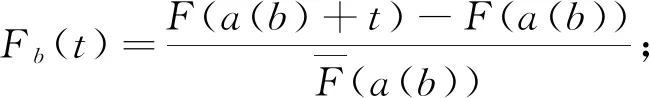
Di—可修产品在保修期内发生第i次失效时的随机维修费用；

H(t)—Di的累积分布函数；

c0—每个产品的生产成本(没有经过预烧测试)；

c1—每个产品在加速环境下预烧单位时间的费用；

c2—不可修产品每次失效所需的替换费用；

c3—可修产品在预烧期间每次失效所需的维修费用；

c4—保修期间产品每次失效的维修或者替换所需的附加费用；

cI—保修策略2中约定的费用上限；

h1(b)—成功预烧一个不可修产品的随机费用；

v1(b)=Eh1(b)；

W1(b)—不可修产品在保修期间的随机费用；

C1(b)—预烧及保修一个不可修产品的总费用；

N1(T)—不可修产品在保修期间的失效次数；

h2(b),v2(b),W2(b),C2(b)，N2(T)分别是可修产品的相关记号；

2.2 假设

本文有如下合理假设

产品具有浴盆型失效率函数；

T与X独立；

c1>c5；

Di(i=1,2,…，)具有相同的分布函数。

本文中的维修指的是最小维修，当维修结束时，经过最小维修的产品的失效率与产品失效前的瞬时失效率相同。

3 加速环境下的失效率模型

在实际中，加速寿命测试(ALT)经常用来在可接受的时间内获得可靠度较高的产品的寿命与时间之间的关系。在此测试过程中，被测试的产品的使用频度要比实际工作环境更高，或者进行测试的环境比实际工作环境更恶劣。进而可以用在这种更强的工作环境下得到的产品的寿命信息预测产品在正常的工作环境下的寿命信息。Nelson[14]提供了加速测试的广泛的背景材料、实践方法、基本理论以及若干例子。Meeker和Escobar[15]对有关ALT的研究状况进行了综述。

加速失效时间(AFT)回归模型是使用最广泛的参数化失效时间回归模型，这种模型可表达为

FA(t)=F(ρ·t)，∀t≥0

(1)

其中ρ是依赖于加速环境的常数。Meeker和Escobar[15]给出了一个更加一般的模型

FA(t)=F(ρ(t))，∀t≥0

(2)

此处ρ(t)依赖于加速环境。由于加速环境与产品的正常工作环境相比，工作压力更大。因此假设在模型(1)中ρ≥1，在模型(2)里对所有的t，ρ(t)≥t，ρ(0)=0。 进一步假设ρ(t)是严格递增，连续且可微的。对于模型(2)，产品在加速环境下的失效率为

对于一个在加速环境下预烧了一个固定的时间b的新产品，如果把它的寿命转化为在一般的预烧环境下的寿命应该不小于b。因此，Cha[12]假设产品在加速环境下预烧了时间b之后，在正常的工作环境下继续工作时寿命的生存函数为

(3)

这里a(b)≥b，∀b≥0，a(0)=0，且a(b)是严格递增、可微的函数。(3)式说明一个产品在加速环境下工作了时间b就相当于在正常的工作环境下工作了时间a(b)。由(3)容易得到加速环境下预烧了时间b之后，在正常的工作环境下继续工作时产品的失效率为

r(a(b)+u)，∀u≥0

联合加速预烧阶段和实际工作阶段，产品在加速预烧时间为b的情形下的失效率函数rb(t)可以表达为

(4)

注意到，在一般的预烧环境下(即ρ(t)=t，∀t≥0；a(b)=b，∀b≥0)。有rb(t)=r(t)对所有的t成立，因此此处考虑的加速预烧模型是一般预烧模型的推广。

4 主要结论

本节，我们首先推导出在加速环境下预烧以及终身免费保修和单次保修费用有上限的终身保修策略下的费用模型。总的费用包括预烧及保修一个产品的总费用。假设预烧时间为b，η-1是直到每次预烧成功一个产品之前，失效的产品个(次)数,{XAi,i≥1}是一列独立同分布的随机变量，分布为FA。

4.1 不可修产品

成功预烧一个不可修产品的随机费用h1(b)为

(5)

h1(b)的均值

(6)

这样就得到了预烧一个不可修产品的费用，接下来在前述两种保修策略下分别得到总费用并得到最佳预烧时间的上界。

4.1.1 终身免费保修

首先来讨论在终身免费保修策略下的总费用的均值最小的最佳预烧时间。不可修产品在终身免费保修策略下的保修费用为

W1(b)=N1(T)·[v1(b)+c4]

则总费用C1(b)=h1(b)+W1(b)=h1(b)+N1(T)·[v1(b)+c4]

这样可以推导出平均总费用为

E[C1(b)]=v1(b)+E[N1(T)]·[v1(b)+c4]

(7)

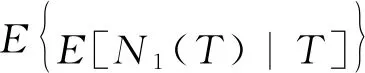
(8)

的最佳预烧时间。

定理1不可修产品在终身免费保修策略下的平均费用为

(9)

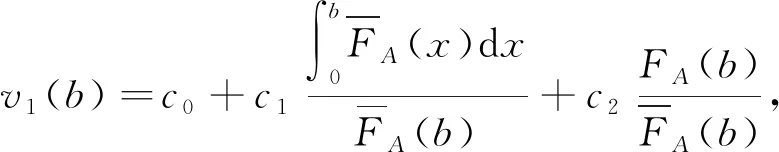
证明通过以上讨论，(9)式显然成立。如果预烧的时间为a-1(t1)， 则平均预烧费用为

分别用rb(t)和ra-1(t1)(t)来表示Fb(t)和Fa-1(t1)(t)的失效率函数，易见rb(t)=r(a(b)+t)，ra-1(t1)(t)=r(t1+t)。因此，可以得到

以及

因此

同时v1(b)当b≥0时是递增函数，所以对于所有的b>a-1(t1)

E[C1(b)]≥E[C1(a-1(t1))]

4.1.2 单次保修费用有上限的的终身保修

接下来研究在单次保修费用有上限的的终身保修策略下的最佳预烧时间。根据保修策略以及第2节中的相关假设，可以得到以下结论。

定理2不可修产品在单次保修费用有上限的的终身保修策略下的平均费用为

(10)

证明令I(b)=min[v1(b)+c4,c1]，则I(b)即为产品在保修期内每次失效所产生的保修费用，则不可修产品在单次保修费用有上限的的终身保修策略下的保修费用为

W1(b)=I(b)N1(T)

4.2 可修产品

成功预烧一个可修产品的随机费用为

h2(b)=c0+c1b+c3(η-1)

(11)

(12)

本小节，同样在两种保修策略下分别得到总费用并得到最佳预烧时间的上界。

4.2.1 终身免费保修

在保修期间产品第i次失效产生的保修费用包括两部分，一部分是固定的附加费用c4，另一部分是随机的维修费用Di，分布函数为H(t)，i=1,2,…。则

W2(b)=(c4+ED1)N2(T)。

定理3可修产品在终身免费保修策略下的平均费用为

(13)

证明产品在实际工作阶段的失效率为rb(t)=r(a(b)+t)，则保修期间的平均保修费用为

E[W2(b)]=(c4+ED1)E[N2(T)]

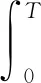
这样就得到了(13)式。

由ρ(t)≥t并且ρ(t)是严格递增的可知，v2(b)关于b是递增的， 又因为r(t)是浴盆型的并且a(b)是严格递增的， 所以当b>a-1(t1)时，

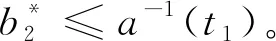
4.2.2 单次保修费用有上限的的终身保修

定理4可修产品在终身免费保修策略下的平均费用为

(14)

E[W2(b)]=E[N2(T)]·E[min(c4+Di,cI)]

这样就证明了(14)式。

注意到v2(b)当b>0时严格递增， 并且E[W2(b)]在区间(a-1(t1),+∞)内是递增的， 所以最佳预烧时间b*≤a-1(t1)。

5 结 论

许多产品在早期具有较高的失效率，因此为了避免产品在实际应用阶段初期失效，我们常采取预烧测试的办法提高产品质量，同时为了减少预烧的花费，预烧过程通常在加速环境下进行。终身保修是一个非常重要的保修策略，在现实生活中的应用会越来越广泛。本文选择了两种典型的终身保修策略，结合加速预烧测试分别对可修产品和不可修产品的平均费用进行了研究，发现最佳预烧时间总是不超过a-1(t1)。

对于结合预烧测试以及终身保修策略研究最佳预烧时间还有很多值得思考的问题，比如把产品的失效进一步分类为最小失效和灾难(毁灭)性失效以及其他的更加合理的终身保修策略等。