三种广义互补蒸发估算公式在华北平原两熟制农田的验证

赵玉杰，韩松俊，张宝忠，张晓龙，赵风华

（1．流域水循环模拟与调控国家重点实验室 中国水利水电科学研究院，北京 100038；2．中国科学院遗传与发育生物学研究所农业资源研究中心 中国科学院农业水资源重点实验室河北省节水农业重点实验室，河北 石家庄 050022；3．中国科学院地理科学与资源研究所 生态系统网络观测与模拟重点实验室，北京 100101）

1 研究背景

华北平原（112°48′E—122°45′E，32°00′N—40°24′N）是我国最大的农业生产区，冬小麦-夏玉米一年两熟的种植模式约占华北平原农田总面积的36%[1]，其对灌溉的依赖加剧了水资源紧缺状况，确定其水分的蒸发消耗对灌溉用水管理至关重要。华北平原冬小麦在每年十月的中、下旬播种，次年六月初收获，夏玉米在每年六月中、下旬播种，同年九月底至十月初收获[2]，在作物收割后至下一种作物出苗前的一段时期（即间作期），地表覆盖接近为裸地[3]。陆面特性的季节变化同时对大气状况造成影响，特别是间作期植被的减少抑制蒸发，引起温度增加、湿度减小[4-5]，甚至引起区域降雨和环流的异常[6]。华北平原两熟制农田的陆面和大气特性的显著季节变化为利用Penman-Monteith公式等侧重陆面过程的方法进行蒸发估算带来了很多困难[7-8]，如无法反映陆面特性变化对区域气候的反馈作用，需要较多陆面信息确定参数等[9]。相比之下，蒸发互补关系通过大气蒸发能力间接反映陆面状况的变化，相应的蒸发估算公式不需要详细的陆面信息[10]，在华北平原两熟制农田蒸发估算中具有一定优势。

互补关系最早由Bouchet[11]在1963年提出，现已从对称的线性关系发展为描述陆面蒸发与大气蒸发能力之间非线性相互作用规律的一种本构关系[12-13]，目前主要存在三种方法：韩松俊等[14-15]的 S型公式，Brutsaert[16]的多项式公式以及Crago和Szilagyi等[17-18]在多项式公式基础上提出的对自变量进行动态标度的方法。前两种方法通过参数考虑植被、土壤水分等陆面特性的影响[19-20]，而在基于动态标度的互补关系公式中，标度系数被认为间接反映了陆面干湿状况的影响[21]。虽然Brutsaert的多项式公式及在其基础上的动态标度方法在不同生态系统取得了良好的效果，但在华北平原两熟制农田，间作期陆面特性变化剧烈，并不确定相关公式是否能够仅利用常规气象数据探知陆面特性变化对蒸散发的影响，因此本文利用四个通量站数据对此进行验证分析。

2 研究数据和方法

2．1 研究站点和数据本研究收集了位于华北平原两熟制农田的四个通量站（禹城、栾城、馆陶和位山）（表1）日或者半小时尺度的气象数据（包括净辐射、土壤热通量、温度、风速、水汽压/相对湿度、大气压强）和通量数据（潜热通量和感热通量）。禹城站和栾城站的数据来自中国通量观测研究联盟（http：//chinaflux．org/），馆陶站的数据来自国家青藏高原科学数据中心（http：//data．tpdc．ac．cn），位山站的数据来自于清华大学位山生态水文观测站。

表1 研究中使用的农田通量站点基本信息

2．2 广义互补公式与韩松俊等[14-15]的无量纲形式的非线性互补公式类似，Brutsaert[22]将传统线性互补关系拓展到无量纲形式：

式中：E为实际蒸发量；Epo和Epa分别为潜在蒸发量和表观潜在蒸发量。式（1）的函数形式为具有一个参数的四次多项式，但一般采用三次多项式（被称为基本式）：

式中：x＝Epo/Epa，y＝E/Epa。Epo/Epa被认为在 0和 1之间，但分别利用 Priestley-Taylor（P-T）[23]公式和Penman[24]公式确定Epo和Epa时，在Epo一定的情况下，即使极端干旱Epa并不一定趋于无穷大，Epo/Epa并不能趋于0。为了满足式（2）的边界条件要求，Crago和 Szilagyi[17-18]先后对自变量 Epo/Epa乘以一个系数，强迫其在极端干旱的情况下趋近于0，得到动态标度的自变量：

式中表观潜在蒸发Epa通过Penman公式计算：

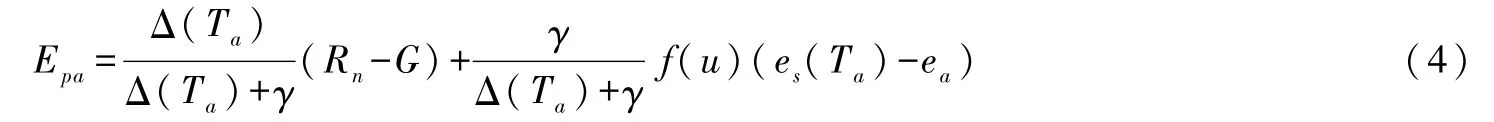
式中：Ta为气温；Δ为对应的饱和水汽压-空气温度斜率；γ为湿度计常数；Rn为净辐射；G为土壤热通量；es（Ta）和 ea分别为Ta下的饱和水气压和实际水汽压；f（u）为风速函数。为Epa的最大值，可通过假设参考高度水汽压为0时的Penman公式计算[18]，即：

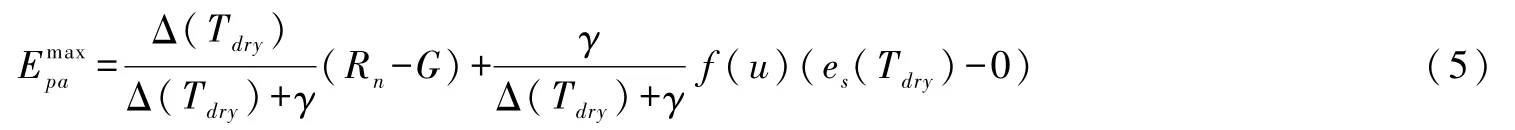
式中：Tdry为假设的区域蒸发为0时的干旱环境的气温，可根据实际气温与水汽压确定[25]。在动态标度方法中，潜在蒸发Epo通过温度修正的P-T公式计算：

式中：Δ（Tw）为假设的湿润环境气温Tw（可通过根据波文比确定的完全湿润环境下的表面温度近似确定[26]）对应的饱和水汽压-温度曲线斜率；α为来自P-T系数的参数，最初采用1．26的默认值，目前被认为是反映陆面干湿状态、植被等因素综合影响的参数。

基于动态标度的广义互补公式在实践中存在两种不同的处理。Szilagyi等[18]直接将标度后的自变量 X带入 Brutsaert[22]的多项式公式：

Szilagyi等[18]提出了利用气象数据提前确定参数 α（约为1．15）的方法，得到了免参数校正的广义互补蒸发估算方法[21-27]。

Crago和Qualls[17]则通过对多个通量站数据的分析认为线性函数更合理：

对于Epo、Crago和Qualls[17]认为不同站点的参数α具有差异，需要通过率定取得。

对于 Epa和中的风速函数也存在两种计算方法，Szilagyi[18]在研究中采用 Penman[24]在 1948年提出的风速函数：

式中u2为地面上2 m高处的平均风速。而Crago和Qualls[17]采用基于 Monin-Obukhov（M-O）相似理论的风速函数：

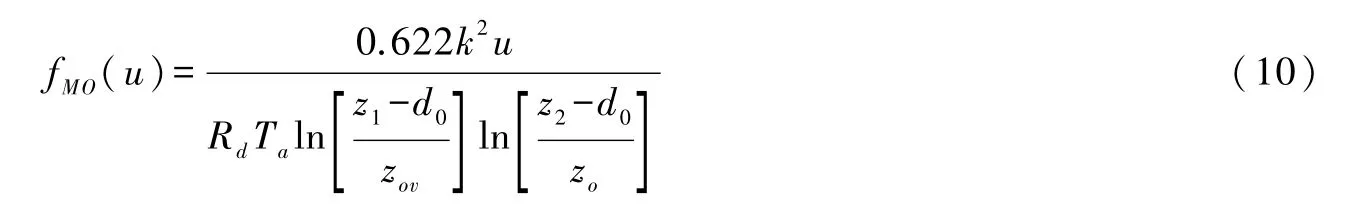
式中：k＝0．41是 Karman常数；Rd＝0．287（KJ/（kg·k））为空气的摩尔气体常量；u为高度 z1处的风速，m/s；z1为风速的测量高度，m；z2为温度和湿度的测量高度，m；d0为零平面位移高度，m；zov为控制动量传输的粗糙长度，m；zo为控制水热传输的糙率长度，m；d0＝0．67hc，zov＝0．123hc，zo＝0．1zov，hc为植被冠层高度。需要指出的是，实际的风速函数随着粗糙度和近地面空气动力学状况的变化具有动态变化，但互补关系的Epa中的风速函数可视为一种参考风速函数[28]，可采用固定的hc确定，在本研究中hc取植被的平均高度1．5 m。

本研究分析对比Brutsaert的多项式公式的基本式、标度后的多项式和标度后的线性公式在华北平原两熟制农田的适用性，并分析两种风速函数对估算效果的影响。在计算中采用半月的时间步长，根据华北平原两熟制农田特点，将一年分为三个阶段进行分析：从十月下半月到次年五月结束的小麦季，从七月下半月到九月结束的玉米季，包括六月、七月上半月和十月上半月的间作期。在数据的质量控制中，我们剔除了明显不合理的数据，包括可用能量（Rn-G）和实际蒸发E小于0的数据、E/Epen大于1．2的数据。研究中使用绝对偏差MAE、均方根误差RSME和纳什效率系数NSE作为评价互补函数公式对实际蒸发量模拟效果的指标，其中纳什效率系数NSE可表示为：

3 结果与讨论

3．1 采用Penman风速函数的不同公式模拟效果图1中给出了采用Penman风速函数并设定参数α为1．26时各站点蒸发比E/Epen与标度前后自变量的散点图。散点分布于式（2）的多项式曲线和式（8）的直线左右，具有一定季节特性，其中小麦季的散点分布偏左，而玉米季和间作期的数据点大部分位于线的右侧，且玉米季散点多位于右上部。散点的季节性分布反映了四个两熟制站点的大气环境受陆面特性变化的影响。三种方法都能较好的模拟实际蒸发量（表2），其中Brutsaert的基本式模拟效果最好，MAE介于 0．25～0．60 mm/d之间，均值为 0．42 mm/d，NSE在 0．73～0．92之间，均值为 0．84；标度后的线性公式模拟效果略差于基本式，MAE在0．25～0．63 mm/d之间，均值为 0．44 mm/d，NSE在 0．68～0．92之间，均值为0．82；而标度后的多项式公式模拟效果最差，MAE在0．37～0．75 mm/d之间，均值为0．54 mm/d，NSE在 0．57～0．84之间，均值为 0．74。

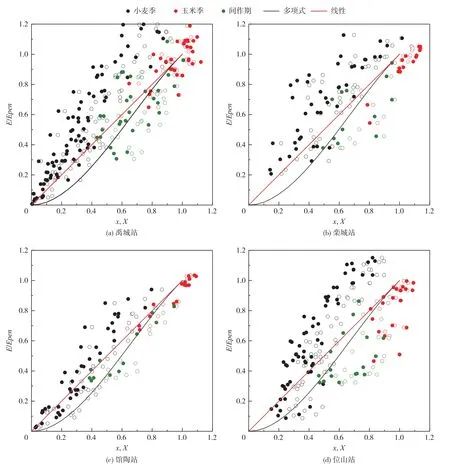
图1 采用Penman风速函数并设定α＝1．26时四个站点标度前后的广义互补关系散点图

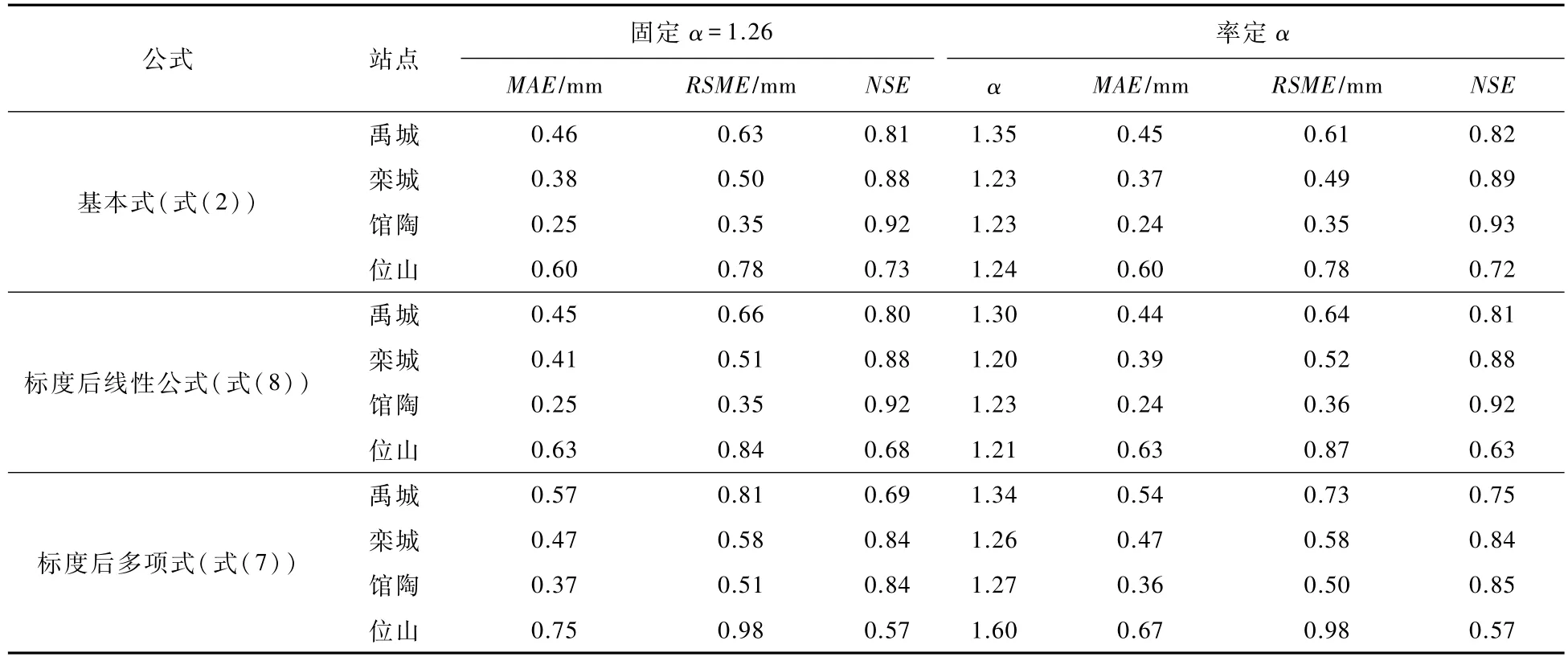
表2 采用Penman风速函数（式（9））并分别固定α和率定参数α时三种公式对实际蒸发的模拟效果

通过最小化MAE对参数α进行率定（表2），基本式的参数α在禹城站为1．35，其他站点在1．23～1．24之间，标度后的线性公式的参数α在1．20～1．30之间，小于基本式的率定值，而标度后的多项式公式参数 α介于1．26～1．60之间，在位山站率定值1．60明显大于另外两种公式的率定值。除部分站点，三种方法率定参数α都在1．26附近，表明α＝1．26在华北平原两熟制农田具有较强的适用性。

3．2 采用M-O风速函数的不同公式模拟效果图2显示，固定参数 α＝1．26并采用 M-O风速函数时，各站点散点分布仍具有季节性特征，但三个公式的模拟效果都差于使用Penman风速函数（表3）。基本式的 MAE增加至 0．35～1．34 mm/d，均值增加了 0．34 mm/d，NSE减小至-0．18～0．84，均值减小了0．37；标度后的线性公式 MAE增加至 0．25～0．78 mm/d，均值增加了 0．10 mm/d，NSE减小到 0．53～0．91，均值减小了 0．10；标度后的多项式公式的 MAE增加至 0．55～1．50 mm/d，均值增加 0．41 mm/d，NSE减小至-0．41～0．61，均值减小0．53。采用M-O风速函数时，基本式在禹城站的模拟效果、标度后多项式公式在禹城站和位山站的模拟效果大幅降低，而标度后的线性公式的模拟效果较好。对参数α进行率定后，采用M-O风速函数的不同公式的模拟效果有一定提高（表3），但基本式在禹城站、标度后的多项式在禹城站和位山站的模拟效果仍然较低。图3显示，固定参数α＝1．26与整体率定α估算的实际蒸发都不能抓住五月的实际蒸发峰值。禹城站率定的α＝1．49（估算的平均日蒸发量为1．94 mm/d），固定参数 α＝1．26（估算的平均日蒸发量为 1．61 mm/d）低估 30．34%。当采用α＝1．26时，基本式和标度后多项式公式分别低估了54．15%和64．61%的实际蒸发。在栾城、馆陶和位山站，整体率定的α值与1．26非常接近，而分阶段率定的 a值在小麦季远大于 1．26（分别为 1．70、1．65和1．86），而在间作期小于 1．26（分别为 1．09、1．19和 1．00）。固定参数 α＝1．26引起对实际蒸发的估算在小麦季低估 29．28%～38．97%，在间作期高估6．29%～24．26%，无法准确反映蒸发量的季节变化。相比之下，采用阶段性参数时，公式能够准确反映实际蒸发量在小麦快速生长季的峰值以及间作期的谷值。

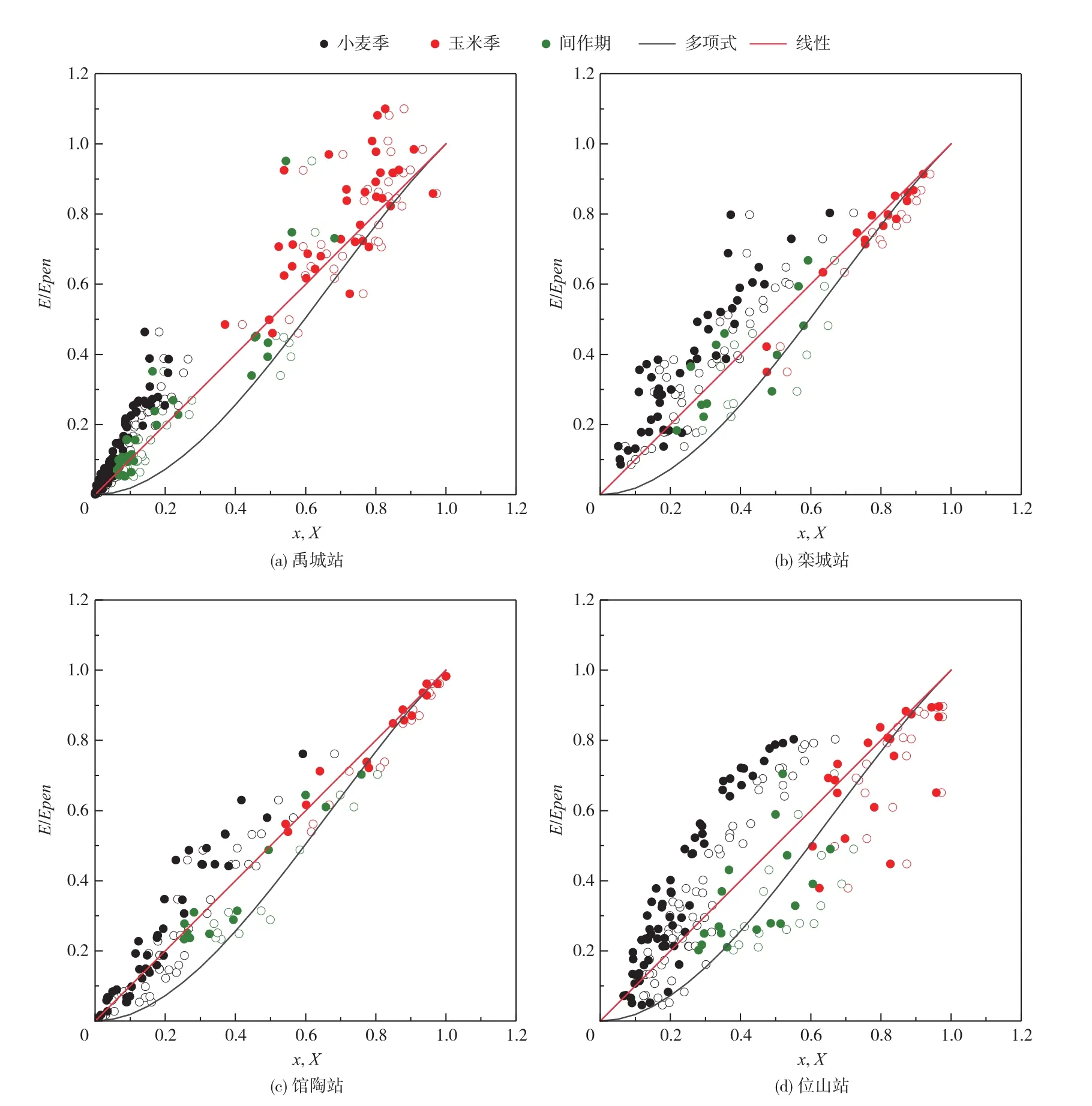
图2 采用M-O风速函数并设定α＝1．26时四个站点标度前后的广义互补关系散点图

表3 采用M-O风速函数（式（10））并分别固定α和率定参数α时三种公式对实际蒸发的模拟效果

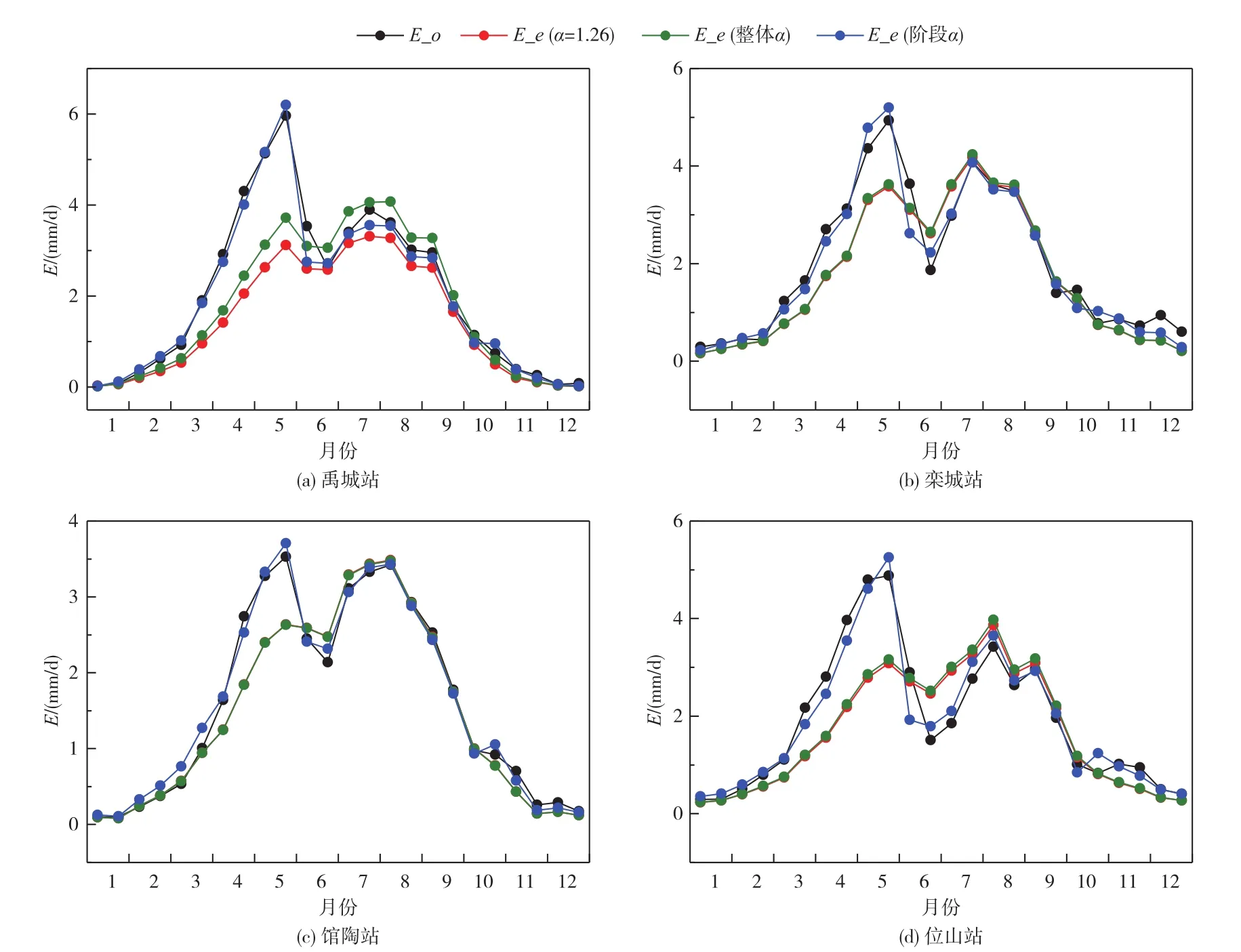
图3 采用不同参数时标度后线性公式估算的实际蒸发与观测值的对比

Penman公式（式（4））是对表观潜在蒸发的近似估算，对风速函数的使用没有确定的结论。M-O风速函数需要通过冠层高度确定动量粗糙度、零平面位移高度和标量粗糙度，这些参数具有季节性变化特征，在研究中我们采用年均冠层高度，未考虑冠层高度的季节性变化，这可能是引起公式在禹城和位山站估算效果较差的原因。Penman风速函数适用于小到中等尺度粗糙度的表面，不需要冠层高度作为参数。对于缺乏表面粗糙度详细信息的情况下，采用Penman风速函数能够合理的估算实际蒸发，但是存在E＞Epen的不合理的现象。

3．3 参数α的季节变化年内使用相同参数时三个阶段数据散点的分布表明广义互补函数公式需要使用不同参数来捕捉季节的变化。在研究中分别率定小麦季、玉米季和间作期不同阶段的参数α，无论采用Penman初始风速函数还是M-O风速函数，线性公式 y＝X和多项式公式y＝（2-x）x2对散点的拟合都更好（见图4和图5），但与图5相比，采用Penman风速函数存在更多自变量和因变量大于1的不合理情况，因此，后续分阶段率定参数时采用M-O风速函数。

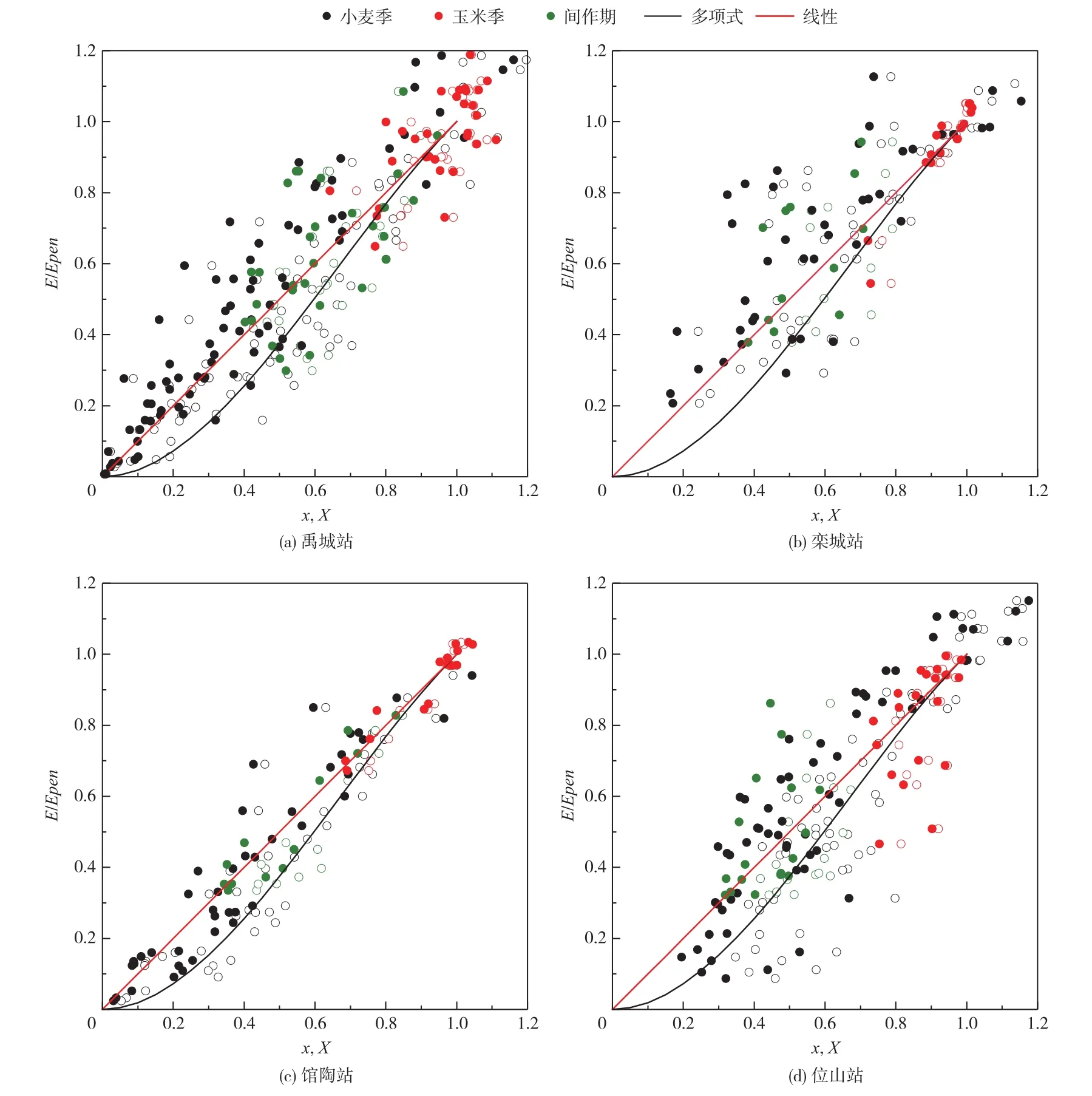
图4 四个通量站采用Penman风速函数分阶段率定参数α的广义互补关系散点图

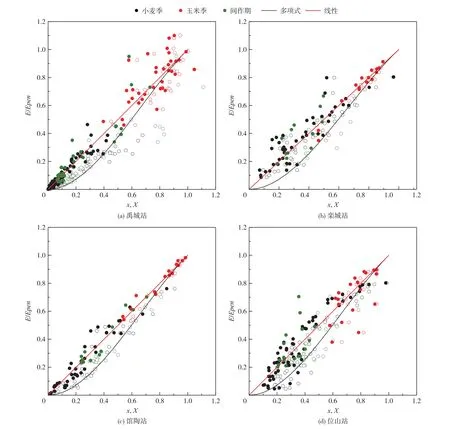
图5 四个通量站采用M-O风速函数分阶段率定参数α的广义互补关系散点图

采用M-O风速函数分阶段拟合参数α后，三种公式都能较好的估算所有站点的实际蒸发，对全年实际蒸发的模拟效果均有较大提高（表4），除禹城站外各公式的MAE减小至0．15～0．50 mm/d，0．10～0．46 mm/d，NSE增加至 0．80～0．97之间，增加了 0．06～0．54。图6显示，采用阶段性参数时，公式能够抓住实际蒸发在小麦快速生长季的峰值以及间作期的谷值。

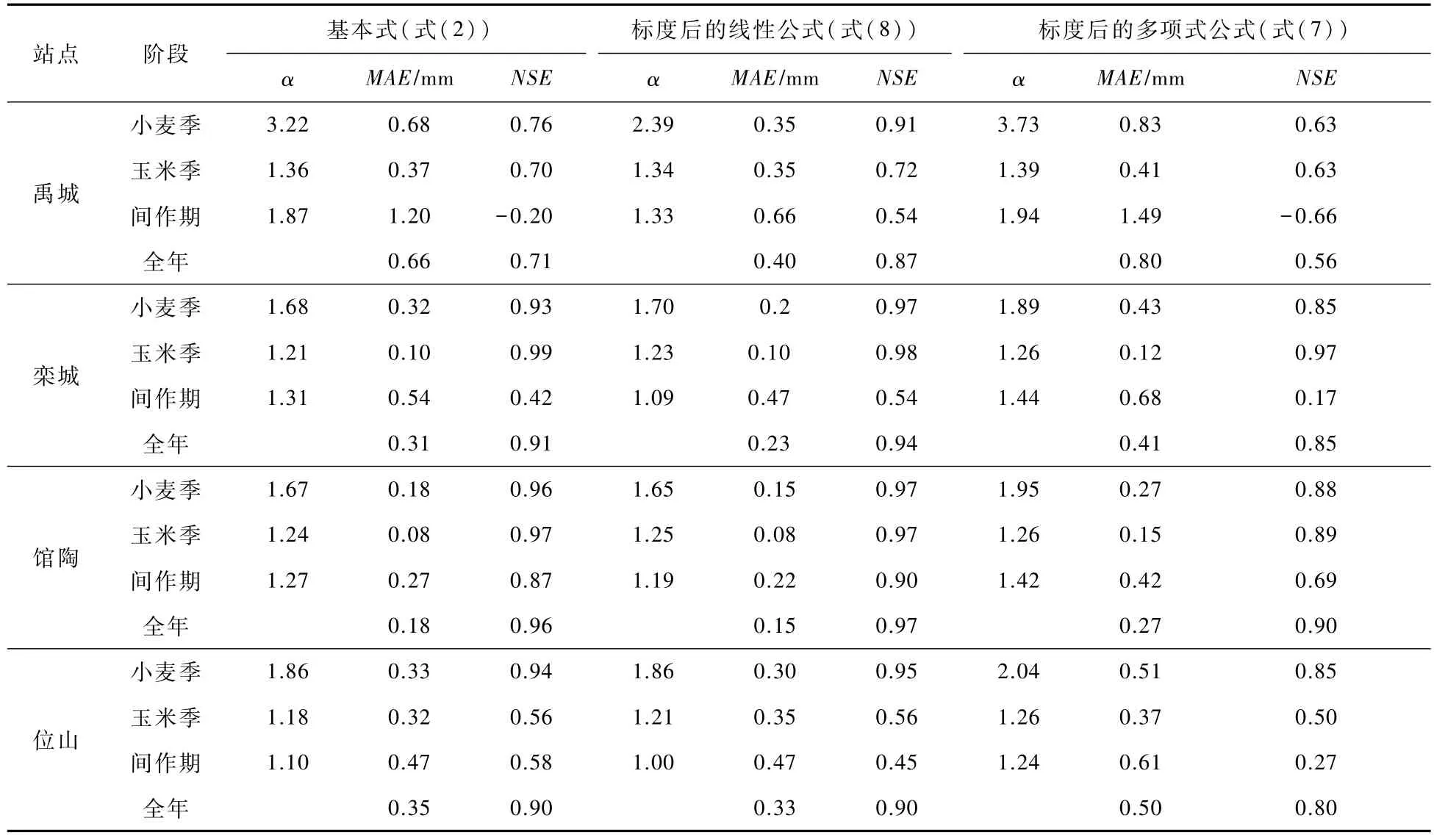
表4 采用M-O风速函数（式（10））时各公式分阶段率定的参数值及其模拟效果

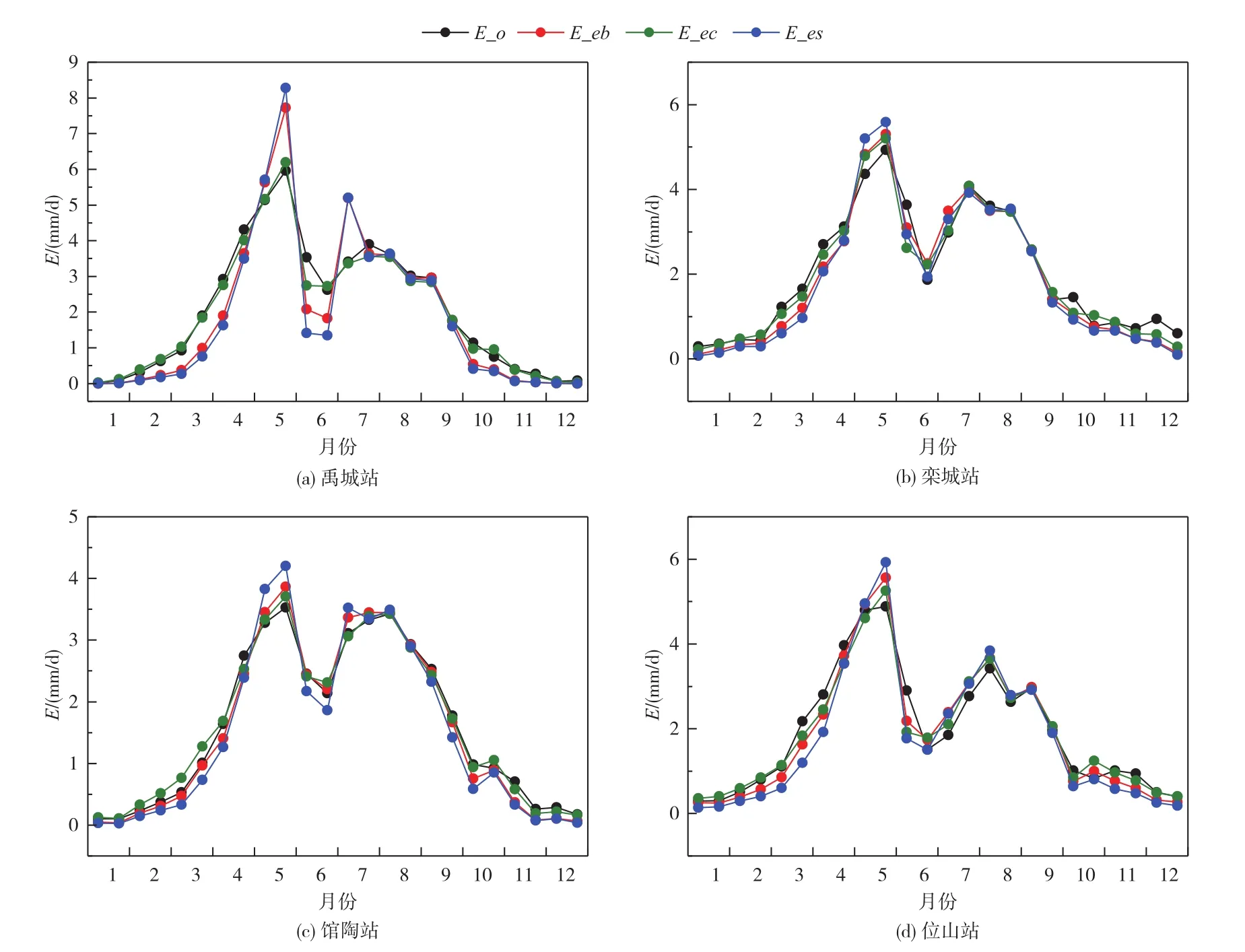
图6 分阶段率定参数对三种公式估算的实际蒸发与观测值的对比

三种公式中，标度后线性公式的模拟效果最优。基本式和标度后线性公式在蒸发比较小时低估，在蒸发比较大时高估。在禹城站，当实际蒸发较小时（十月至次年四月、六月），基本式和标度后多项式公式对实际蒸发的低估量分别为30%和38%，当实际蒸发较大时，两种公式对实际蒸发分别高估33%和36%。标度后线性公式（8）能够较好反映实际蒸发的季节变化，估算效果优于基本式和标度后多项式公式，MAE分别降低 0．02～0．26 mm/d和 0．12～0．40 mm/d，而 NSE分别增加了 0～0．16和 0．07～0．31。

互补原理最初期望利用常规气象数据能够准确及时地捕捉到陆面状况的变化[29]，这样可以采用固定的α值。但仅大气状况的变化可能并不能完全反映陆面状况对蒸散发过程的影响[13]，且受到大尺度气候条件变化的影响，造成参数α并不固定，受陆面水分条件和植被状况等因素的影响而发生变化[30]。杨汉波等[31]的研究也表明互补关系中的参数α具有显著的季节性。在华北平原两熟制农田，小麦季、玉米季和间作期的水分条件和植被状况具有显著差异，因此参数α明显不同，而分阶段率定效果更好，这也表明三种公式都可通过参数的变化来适应环境的变化。

4 结论

本文以华北平原四个冬小麦-夏玉米两熟制农田通量站为研究对象，分析了Brutsaert的广义互补多项式公式的基本式以及基于动态标度的线性和多项式公式的适用性。主要得出了以下结论：

（1）采用Penman风速函数时，三种公式都能有效地模拟华北平原两熟制农田的实际蒸发量，公式中的参数可设定为α＝1．26，Brutsaert的基本式对实际蒸发的估算效果最好。

（2）标度后的线性公式受风速函数影响最小，且适用于所有两熟制农田站点，而基本式和标度后多项式公式在采用M-O风速函数不能有效的反映实际蒸发的季节变化。

（3）分小麦季、玉米季和间作期分别拟合参数α不仅能够显著提高三种广义互补公式对实际蒸发量的估算精度，同时可以缩小不同公式对实际蒸发量模拟的差距。