一种基于水滴收集量代理模型的结冰试飞空域确定方法

牛俊杰，桑为民，2，*，李栋，郝莲，王泽林

1．西北工业大学 航空学院，西安 710072

2．中国空气动力研究与发展中心 结冰与防除冰重点实验室，绵阳 621000

3．中国商用飞机有限责任公司 上海飞机设计研究院，上海 201210

4．中国飞行试验研究院，西安 710089

飞机在含有过冷水滴的云层中飞行时，会在其表面产生结冰。飞机结冰会严重威胁飞行安全［1-2］。据 统 计，仅2003—2008年 间 就有380余起与结冰相关的飞行事故［3］。中国自2006年6·3空难以来，飞机结冰以及由此引起的飞行事故越来越受到关注，特别是大飞机项目的启动，使得与飞机结冰相关的研究成为研究热点［4］。适航规章规定飞机必须经过结冰适航审定才能够容许在结冰环境下飞行［5-6］。飞行试验验证的目的是验证飞机在结冰条件下飞机的飞行性能、飞行品质能够满足适航审定要求，防除冰系统能够履行其功能。与美国、欧洲等航空事业较发达的国家相比，中国飞机结冰适航验证工作起步较晚。中国虽然完成了Y12-II、Y7-200A、ARJ21-700等飞机结冰适航验证，但在适航验证方法和许多关键技术方面与国外差距较大，尚未形成系统的飞机结冰适航验证和试飞技术［7］。通常飞行试验验证分为干空气飞行试验、带模拟冰型的飞行试验和自然结冰飞行试验3类。自然结冰试飞试验是在自然结冰状态下，验证飞机在暴露于适航条例规定的连续和间断最大结冰状态下能够安全运行，其系统能够达到预定的功能和性能。自然结冰试飞试验的关键是寻找适合的结冰气象条件，在一定的结冰气象条件下进行试飞试验，验证飞机的各项功能满足适航要求。中国基于自然科学研究的结冰探测试验过程“屈指可数”，完整的结冰探测试验过程的具体数量尚没有权威的统计，主要有：1986—1987年Y-12II在新疆完成了5次结冰试飞［7］；1997年Y7-200A飞机自然结冰飞行试验选择新疆天山地区为试验区，在满足飞机自然结冰条件时进行了2次自然结冰试飞工作［8］；2018年中国生产的某型直升机在新疆五家渠自然结冰试飞［9］以及从2011年开始ARJ21结冰试飞［10］。ARJ21首先在新疆进行结冰试飞，最终在加拿大完成结冰试飞全部科目［10］。从中可以发现中国之前的结冰试飞主要在新疆以及加拿大完成。ARJ21前期连续3年在新疆找结冰环境，真正飞成功的架次较少，之后去了北美五大湖1.5个月完成结冰试飞所有科目。从实际业务发展需求角度出发，自然结冰试飞气象预测已成为严重制约国产大飞机的研制和交付使用的一个重要方面［10］。

在自然结冰试飞过程中，常常使用结冰指数来表征可能结冰的区域以及结冰强度，如：基于Schultz和Politovich研 究 成 果 的Icing Indices［11］，该指数基于温度和相对湿度对结冰概率进行预测，结冰概率为温度与湿度的函数；由Belo-Pereira提出一种新的结冰指数SFIP（Simplified Forecast Icing Potential），该指数基于数值气象预测的结果，认为结冰指数是温度、相对湿度以及液态 水 含 量（Liquid Water Content， LWC）的 函数［12］；Politovich和Sand提出的一种结冰严重指数［13］，该指数考虑影响结冰的3个主要参数：大气环境温度、云中过冷水含量及云滴的中位数体积直径；Thompson等提出结冰方案，该方案根据每个探空层上的温度（T）、露点（Td）以及在本层与上层之间的温度递减率，确定该层的结冰强度和类型，结冰强度划分为8个等级［14］；Thompson等提出的RAP（Research Applications Program）算法根据温度、相对湿度定义了4种结冰类型：层状、冻雨、不稳定、普通［15］；NCAR （National Center for Atmospheric Research）提出模糊逻辑预报方法，该方法是将和结冰有关的温度、湿度、云量、云水等与结冰的可能性相联系，做成曲线，找出各种情况下的结冰可能性和结冰强度，该方法又被称为当前结冰潜势分析（Current Icing Potential，CIP）［16］。李佰平等［10］对自然结冰潜势算法进行了改进，该算法直接基于大气温湿层结给出结冰潜势。

然而使用结冰指数大多只能给出结冰的可能性或者对结冰强度进行预测。飞机结冰受到多种因素的影响，包括结冰气象因素（如温度、液态水含量、水滴中值体积直径以及高度等）和飞行状态因素（如速度、前缘直径、攻角以及结冰时间等）。一般而言，温度主要影响冰的形态，液态水含量以及速度影响结冰量，水滴中值体积直径影响水滴的撞击极限位置，高度影响温度。然而，温度会对液态水含量产生影响，温度越低，空气中的液态水含量越低。这是由于空气中的过冷液态水会随着温度的降低逐渐向冰晶转化，进而导致液态水含量的降低。当温度低于−40 ℃时，被认为很少有过冷液态水存在［5］。结冰气象因素属于不可控因素，需要特定的天气条件，而飞行状态因素中速度和时间是可控因素。因此在一定的结冰气象条件下，可以通过调节飞行速度或者时间达到使结冰气象条件达到满足结冰试飞的条件。

因此，提出一种基于水滴收集量代理模型结合WRF（Weather Research and Forecasting Model）气象预测的结冰试飞空域确定方法。首先对美国联邦航空条例（FAR）25部附录C进行采样，对采样点进行空气流场和水滴流场数值模拟，获得不同采样点下翼型的水滴收集量，利用本征正交分解（Proper Orthogonal Decomposition，POD）方法及Kriging插值建立气象因素（温度、高度、液态水含量、水滴中值体积直径）、飞行状态（速度、高度）与水滴收集量之间的代理模型。基于WRF获得的气象条件，结合水滴收集量代理模型，则可以获得目标区域内水滴收集量的空间分布及随时间的变化，以中度结冰强度对目标区域的水滴收集量进行划分，进而获得可用于结冰试飞的空域并且对结冰强度进行预测。

1 计算方法及控制方程

基于水滴收集量代理模型及WRF气象预测的结冰试飞空域确定包括2部分内容：一部分为水滴收集量代理模型构建，另一部分为WRF气象条件预测。在水滴收集量代理模型构建中，采用优化拉丁超立方采样对附录C进行采样，获得连续最大结冰状态下的40个采样点，对采样点进行空气流场和水滴撞击特性计算，获得不同采样点工况下的水滴收集量。采用POD方法和Krig⁃ing插值构建水滴收集量的代理模型。采用WRF进行气象预测，获得目标区域内的气象参数，然后基于气象参数和水滴收集量代理模型，对目标区域进行水滴收集量快速预测，获得目标区域内水滴收集量的空间分布及随时间的变化，以中度结冰强度对目标区域的水滴收集量进行划分，进而获得可用于结冰试飞的空域并且对结冰强度进行预测。结冰试飞区域确定流程如图1所示。在本节中对水滴收集量的代理模型构建进行说明，WRF气象预测的说明见2.2节。

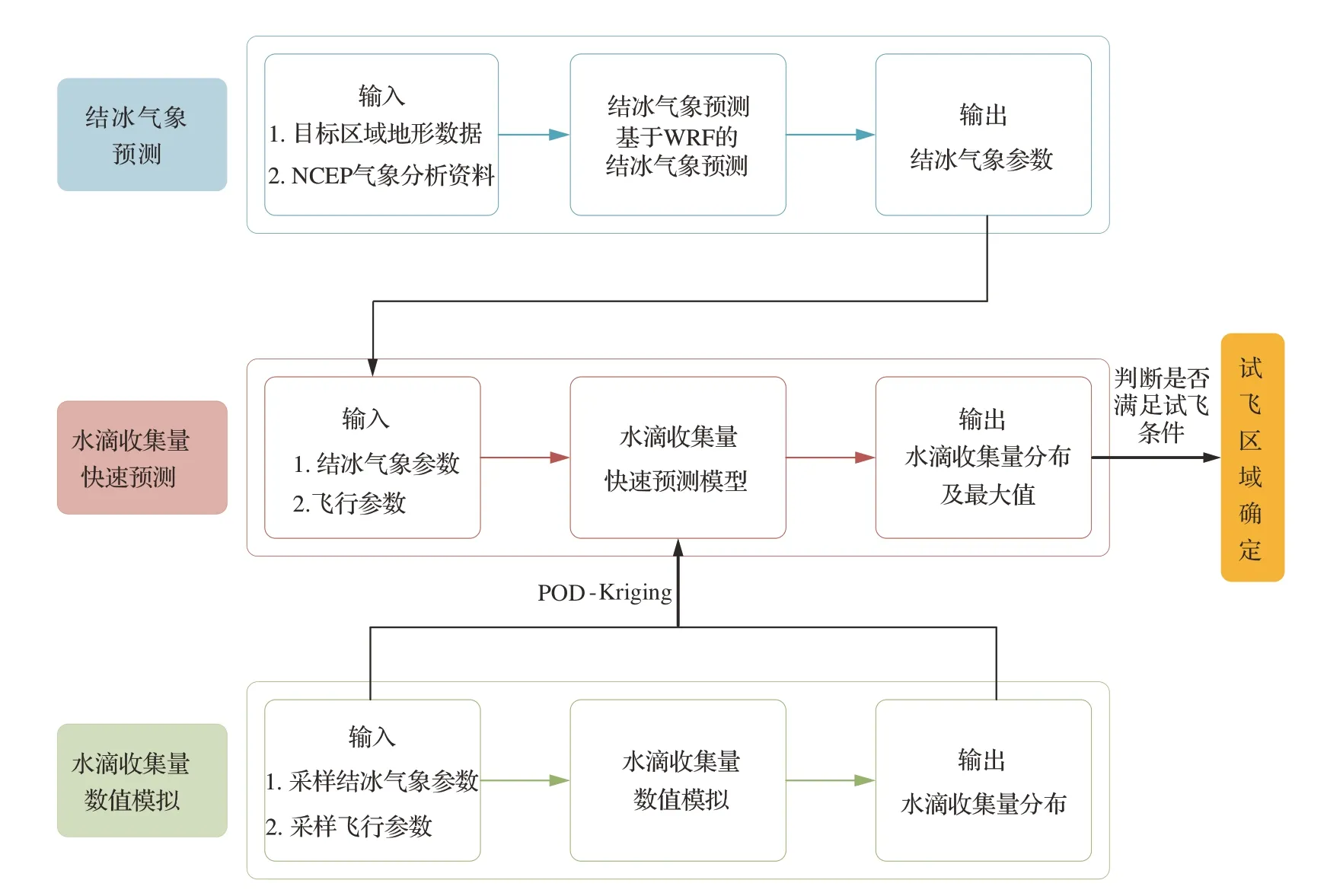
图1 结冰试飞区域确定流程Fig. 1 Flow chart of icing test flight area determination

1.1 水滴撞击特性求解

结冰数值模拟过程通常包括空气流场求解、水滴撞击特性求解以及结冰传热传质模拟3部分内容。本文旨在求解壁面处水滴收集量分布，因此只针对上述计算过程中前2个步骤进行数值模拟，即空气流场的求解和水滴撞击特性求解。在空气流场求解的基础上，采用拉格朗日方法建立过冷水滴运动方程，并进行求解，获得过冷水滴的撞击特性及壁面水滴收集量分布。

空气流场通过求解Navier-Stokes方程组获得，方程组的张量形式为

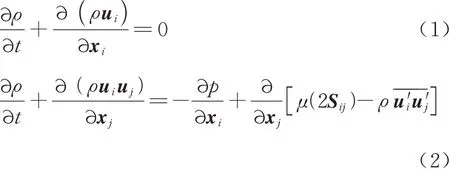
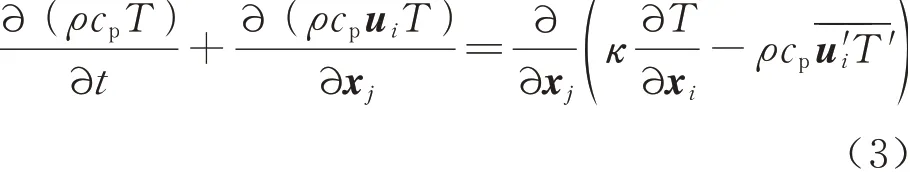
式中：ρ为空气密度；t为时间；u为空气速度，下标i、j为张量指标；x表示方向；p为压力；Sij为应力张量；μ为空气动力黏性系数；cp为空气定压比热容；T为温度；κ为空气导热系数分别为湍流应力张量和湍流热流通量。湍流模型采 用SST（Shear Stress Transport）k-ω湍 流 模型［17］，空气流场求解使用SIMPLE算法，压力、动量、湍流动能和能量项以二阶方式离散。压力和动量松弛因子为0.4，收敛精度设定为10−6。在获得空气流场分布基础上，采用拉格朗日法获得过冷水滴的运动轨迹。拉格朗日法对水滴轨迹进行求解时，对每个水滴进行跟踪，其中假设［18-19］：水滴在运动过程中既不相互碰撞也不分解，水滴的密度、温度等在运动中保持不变；水滴的初速度与自由来流相同，水滴流场不会对空气流场产生影响。水滴的运动轨迹及撞击位置如图2所示。

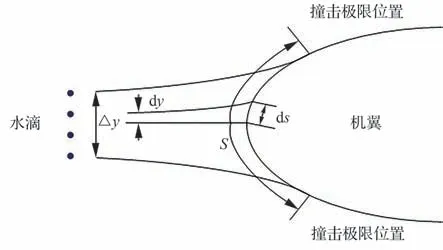
图2 水滴轨迹示意图Fig. 2 Schematic diagram of water droplet trajectory

水滴的运动过程可以表示为

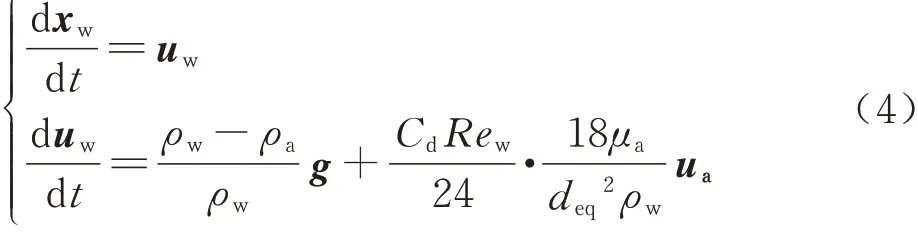
式中：uw为水滴速度；ua为空气速度；ρa为空气密度；ρw为水滴密度；g为重力加速度；Cd为水滴曳力系数；deq为水滴直径；μa为空气黏性系数；Rew为相对雷诺数，定义为

在计算得到空气流场的结果后，采用四阶龙格-库塔法对式（4）进行求解，获得了水滴的运动轨迹及撞击位置。由水滴的初始位置和碰撞位置，得到局部水滴收集系数β：

式中：dy为初始位置时相邻水滴的距离；ds为相邻水滴翼面碰撞位置的距离，水滴位置如图2所示。壁面水滴收集量为

其中：LWC为液态水含量；V∞为远场速度；β为水滴收集系数。

1.2 POD方法

本征正交分解（Proper Orthogonal Decom⁃position，POD）是一种数值方法，可以降低计算流体力学和结构分析等计算模拟的复杂性。通常在流体动力学和湍流分析中，其用更简单的模型来代替Navier-Stokes方程［20-21］。假设存在这样的物理场y=y（x， tn），该物理场可以表示为无穷级数的形式：

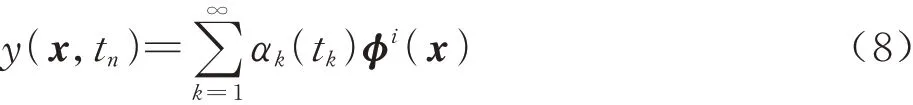
式中：ϕi(x)为特征基函数；αk(tk)为经验系数；tn为参数变量。利用相关的数学理论可将式（8）转换为求解特征值的问题：

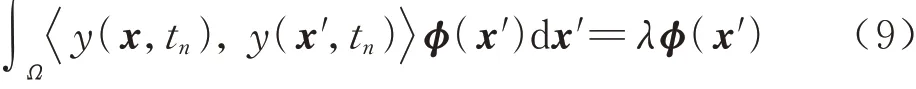
其中： 为内积符号；λ为特征值。在实际使用中，可应用快照方法将式（9）转换为一个与快照个数N相等的特征值问题。若一个样本包含M个数据，则取N个样本组成一个样本集U={U1，U2，…，UN}，特征基函数可以由快照的线性组合构成，即

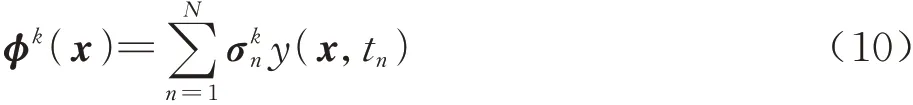
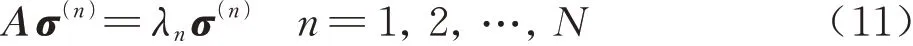
式中：λn为特征值。A中各元素为

其中：矩阵A的特征值大小代表该正交基函数在整个样本空间中所占能量的比重。因此进行物理场重建时便可以根据能量的大小对基函数进行筛选，而并不需要选择所有的基函数。假设选用了M个正交基函数，则有M≤N。在进行矩阵分解得到最佳正交基后，对选取的正交基与样本进行内积即可得到对应的系数：

因此，重构的物理场可以使用正交基的线性叠加表示为

1.3 Kriging插值

Kriging插值方法是20世纪50年代由南非工程师Krige所提出的［22］，已广泛应用于各个领域。在飞机结冰和防/除冰领域，Pellissier等［23］基于POD、Kriging方法以及遗传算法，以喷射角、喷射间距及前缘距离为控制变量对防冰腔布局进行了优化设计；刘藤等［24］建立了基于POD方法和Kriging模型的冰形快速预测方法，从而实现了多参数的冰形快速预测。

假定N个快照的系数α定义了Rk中N个超平面α（x），其中k为自由参数的数目，x为设计变量，x=[x1，xx，…，xk]T，寻找α（x）的问题也就转变为超平面中的多维插值问题。Kriging插值具体原理为

Kriging插值将未知函数视为一个高斯随机过程，该随机过程可以表示为

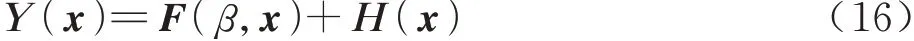
式中：F(β，x)为全局趋势模型；H(x)为随机分布的误差；x为参数变量。

使用协方差来表示不同相关点处随机变量的相关性，即

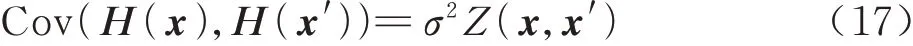
式中：σ2为方差；Z(x，x')为相关函数，只与空间距离有关。Kriging模型寻找最优加权系数ω，可使得均方差最小，并且满足无偏差条件。通常使用式（18）获得Kriging模型的预估值：

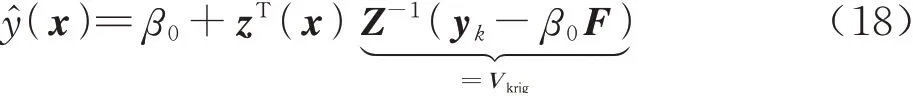
其 中 ：Vkrig只 与 样 本 点 有 关 ；β0=(FTZ−1F)−1FTZ−1yk，yk为样本数据，F为一维单位向量，Z和z分别为前述相关函数矩阵及其中的相关向量，因此可以利用样本数据得到模型的估计值。关于POD和Kriging的详细介绍可以参考文献［24］。

2 数值模拟验证

对NACA0012翼型进行数值模拟，获得壁面水滴收集系数分布，与文献［25］中结果进行对比，以验证水滴撞击特性数值模拟的准确性。NACA 0012水滴撞击特性验证工况如表1所示。

表1 水滴撞击特性验证算例工况Table 1 Conditions of water droplets impingement characteristics validation cases

2.1 NACA0012水滴撞击特性验证

图3和图4分别为NACA0012翼型周围网格示意图和水滴轨迹示意图。图5为NACA0012翼型表面水滴收集系数分布对比，其中实线为本文模拟结果，三角和黑色点划线为文献［25］中结果。横坐标（S−Ssp）/C表示壁面点与滞止点之间的距离与弦长的比值。图中可以看出本文模拟结果与文献结果符合良好。由于来流攻角为4°，水滴碰撞到上翼面范围较小、下翼面范围较大，相应的水滴收集系数在驻点附近达到最大值，下翼面处水滴收集系数变化相较于上翼面更为缓慢，水滴撞击极限也相对较大。

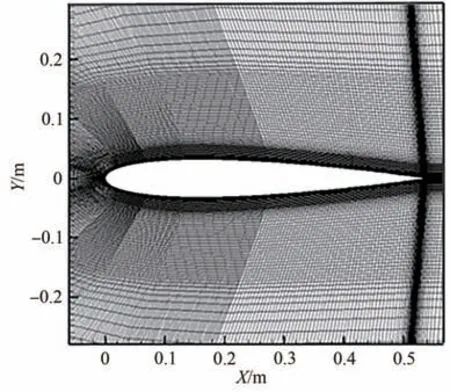
图3 NACA0012网格示意图Fig. 3 Schematic diagram of NACA0012 mesh

图4 NACA0012水滴轨迹示意图Fig. 4 Schematic diagram of droplet trajectory around NACA0012

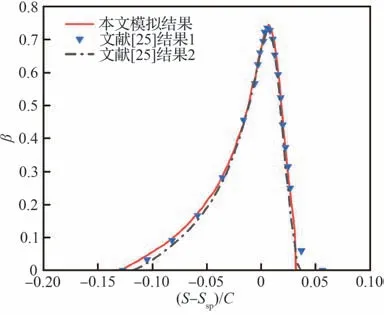
图5 NACA0012表面水滴收集系数分布Fig. 5 Distribution of droplet collection coefficient on NACA0012 surface

2.2 WRF气象模拟验证

WRF是中尺度数值天气预报系统，适用于高分辨率大气模拟。WRF模型由许多不同的物理方案组成，包括对微物理、积云参数化、表面物理、行星边界层以及大气辐射的不同描述。各种物理方案的介绍可以参考文献［26］。在本文研究中微物理方案采用Morrison等［27］方案，该方案适用于液滴、云冰、雨、雪的数值模拟。积云参数化 方 案 采 用Kain-Fritsch方 案［28］。行 星 边 界 层（Planet Boundary Layer， PBL）方案采用延世大学（YSU）PBL方案［29］。气象预测的初始边界条件采用美国国家环境预测中心（National Centers for Environmental Prediction， NCEP）的FNL再分析数据（数据精度为1°×1°）。

WRF可以获得诸如温度、压力、液态水含量等参数。在WRF中可以直接输出温度、压力以及云水混合比等参数，液态水含量可以通过云水混合比（Qcloud）获得，具体方式为

在本文中，假设当温度低于273.15 K时，则认为液态水为过冷态，并且液态水温度与空气温度一致。云层中的液滴在与空气进行长时间的热量交换后，可以认为液滴与空气处于平衡态，液滴温度与空气温度一致。Cober等［30］指出，CASP （Canadian Atlantic Storms Program） II曾开展了31架次共119 h的结冰飞行试验，对冷锋、暖锋、低压区域以及低空层云中的中值体积直径MVD （Median Volume Diameter） 进 行 统 计，发现冷锋、暖锋、低压区域云中的MVD平均值为20 μm，低空层云中的MVD平均值为16 μm。因此在本文中MVD则统一假定为较大值20 μm。

由于结冰试飞气象条件比较苛刻且文献中可用的数据较少，因此本文选用2013年4月1日华盛顿山（44.267N，71.3W，海拔1 917 m）的结冰事件进行数值模拟，获得的温度和液态水含量LWC的结果与实际观测数据和文献［31］中的结果进行比较。采用3层区域嵌套，内外层网格分辨率分别为9、3、1 km，最内层区域内采用225×225×26个网格点进行数值模拟。图6为嵌套区域的示意图。

图7为华盛顿山温度随时间的变化与文献［31］结果的对比。其中黑色原点为观察值，实线为本文模拟结果，虚线为文献［31］中的模拟结果。

图8为华盛顿山LWC随时间变化与文献［31］结果的对比。与图7类似，黑色原点为观察值，实线是本文模拟结果，虚线是文献［31］中的模拟结果。

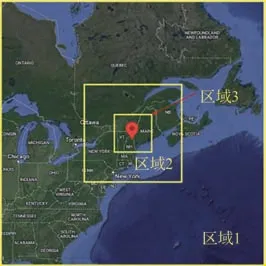
图6 嵌套区域示意图Fig. 6 Schematic diagram of nested domains

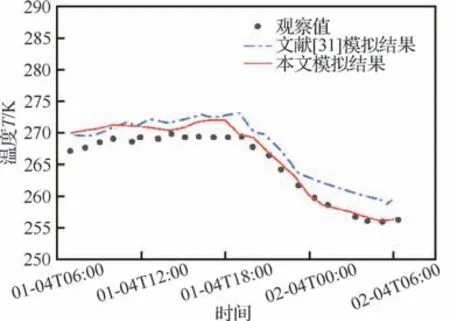
图7 温度随时间变化对比Fig. 7 Comparison of temperature variation with time

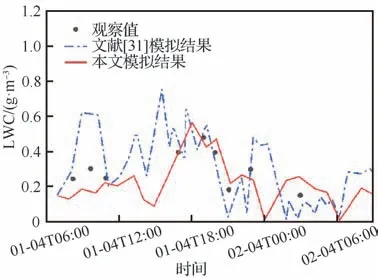
图8 LWC随时间变化对比Fig. 8 Comparison of LWC variation with time

分别以平均绝对误差（Mean Absolute Er⁃ror， MAE）、均 方 根 误 差（Root Mean Squared Error， RMSE）、平均绝对百分比误差（Mean Ab⁃solute Percentage Error， MAPE）对预测结果与试验结果以及文献［31］中的结果进行比较，其具体定义见式（20）~式（22）。

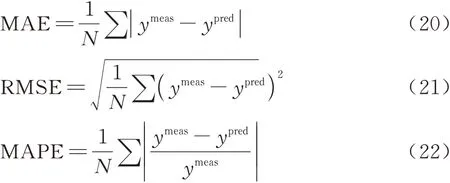
式中：ymeas和ypred分别为结冰气象参数观测值与模拟结果。

表2为结冰气象参数温度、液态水含量预测结果与观测结果以及文献［31］预测结果与观测结果的误差对比。可以发现无论温度还是液态水含量，本文预测结果均要好于文献中结果，平均绝对误差、均方根以及平均绝对百分比误差均较小。温度T的平均绝对误差为1.45 K，平均绝对百分比误差为0.5%；液态水含量的平均绝对误差为0.07 g/m3，平均绝对百分比误差为25.6%，好于文献［31］中的结果28.7%。

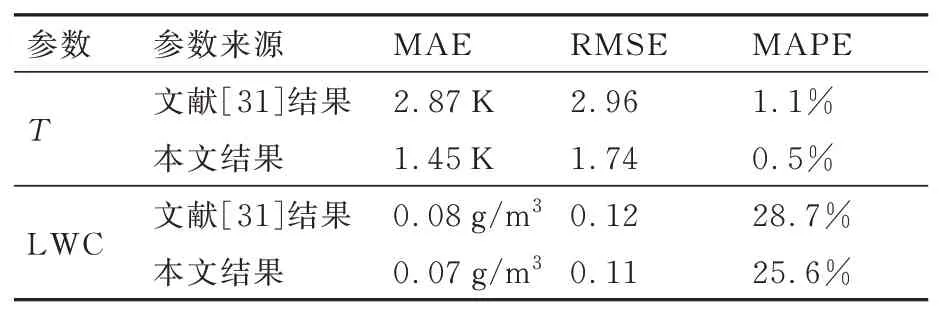
表2 结冰气象预测误差分析Table 2 Error analysis of icing weather prediction

3 结果与讨论

3.1 水滴收集量代理模型

通过对FAR 25部附录C中连续最大结冰条件进行优化拉丁超立方采样，获得40个工况点，采样点分布如图9所示。以NACA0012翼型为模型，分别对40个采样点进行数值模拟，获得不同工况下的水滴收集量分布，其中部分采样点工况如表3所示。NACA0012网格如图3所示。

图10为表3中工况下水滴收集量分布云图。图11为表3中采样点水滴收集量在翼面分布的对比。其中横坐标Y/C表示翼面位置Y坐标与弦长C的比值，其中正值表示上翼面，负值表示下翼面。NACA0012位置示意图可参考图3。从图10和图11可以看出，在翼型前缘处水滴收集量最大：受攻角的影响，水滴收集量的最大值出现在翼型前缘下沿；而在前缘点之后沿着翼型表面水滴收集量逐渐减小，下翼面水滴收集量变化相较于上翼面更为缓慢，水滴撞击极限也相对更大。与此同时，水滴收集量极值以及撞击极限受LWC、MVD、温度、高度、来流速度等因素共同影响。水滴收集系数极值受LWC和来流速度的影响较大，如Case 1与Case 4。而由于直径（或质量）较大、速度较大的液滴具有较大的惯性，在撞击机翼表面时液滴轨迹不易发生改变，因此水滴撞击极限范围通常随MVD和来流速度增大而增加，如Case 4与Case 5。

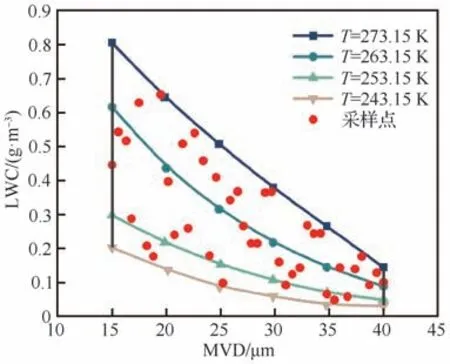
图9 采样点分布Fig. 9 Distribution of samples

图12为水滴的撞击范围，横坐标表示翼面位置X轴坐标与弦长C的比值，NACA0012位置示意图可参考图3。撞击范围内一共139个点，40组工况则可以构成139×40的矩阵，对该矩阵进行POD降阶，获得对应的特征向量及系数。

图13给出了壁面处水滴收集量最大误差随积累特征值的变化。图中可以看出随着积累特征值的增加，最大误差迅速减小，当积累特征值达到20时，水滴收集量最大误差减小至接近于0。说明采用POD方法可利用少量特征基函数对原物理场进行重构。因此在本文中使用前20个特征基函数即可满足精度要求。对于非采样点（即预测点）处的系数，需要通过Kriging多维插值获得。即针对非样本点，需要对前20个系数分别进行Kriging多维插值，获得20个对应的系数。本文的Kriging插值使用MATLAB的OODACE工具箱完成。最终，壁面的水滴收集量分布可以由20个特征基函数及对应的系数相乘后获得。

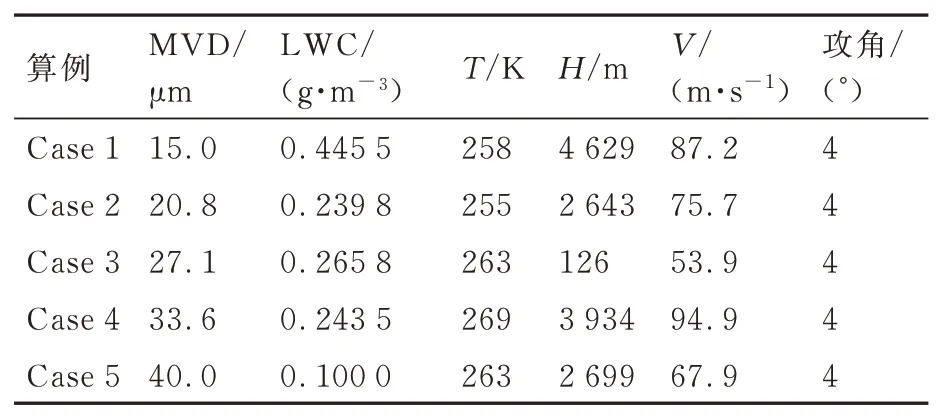
表3 部分采样点工况Table 3 Conditions of part samples

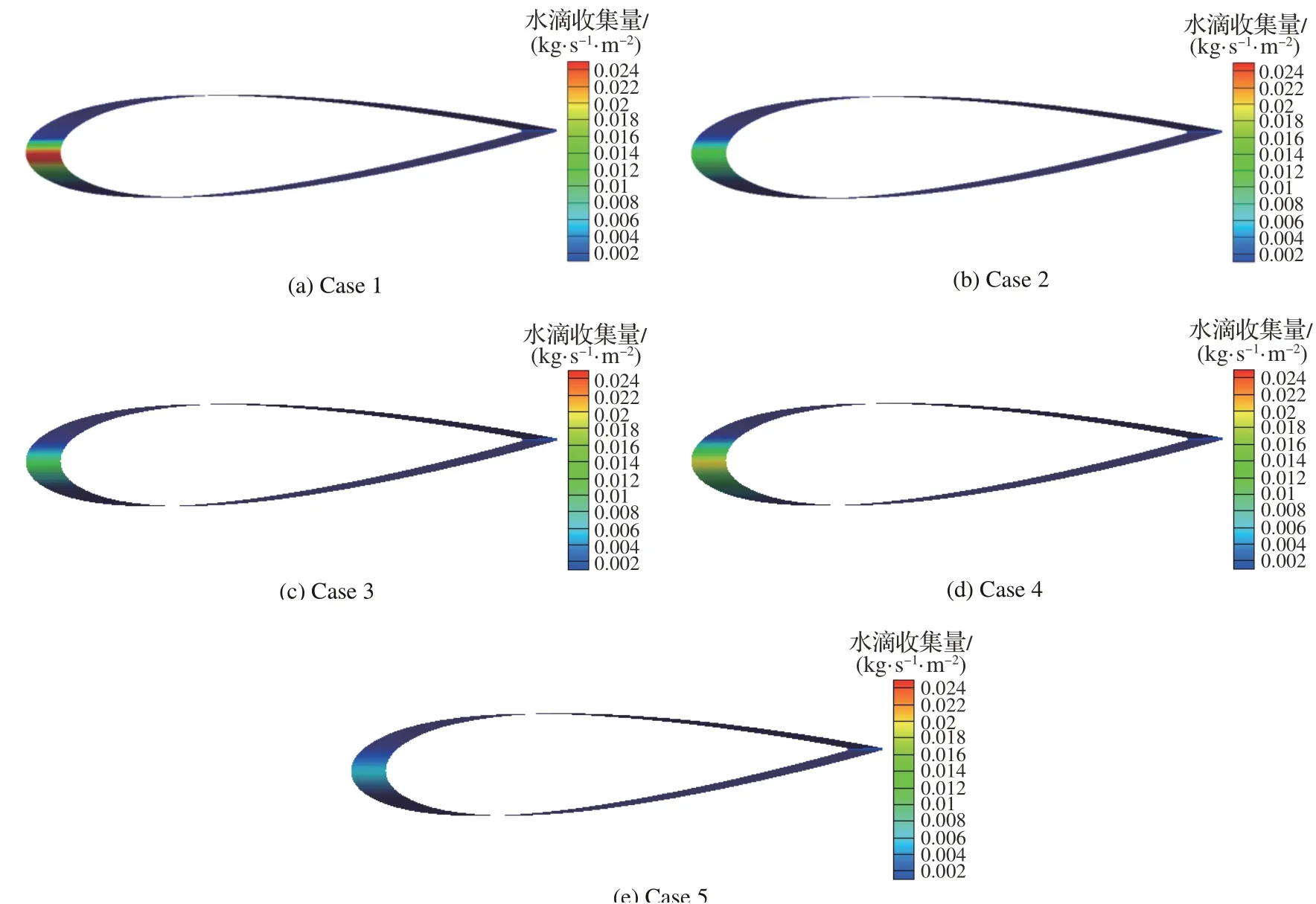
图10 Case 1~Case 5水滴收集量云图Fig. 10 Water droplet collection amount contours of Case 1-Case 5

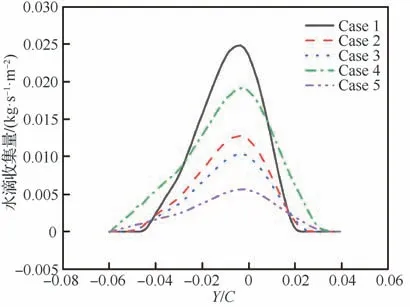
图11 Case 1~Case 5水滴收集量分布Fig. 11 Water droplet collection amount distributions of Case 1-Case 5

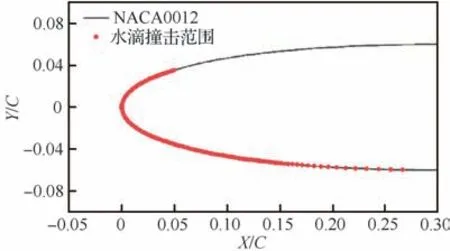
图12 水滴撞击范围示意图Fig. 12 Schematic diagram of water droplet impinge⁃ment extent

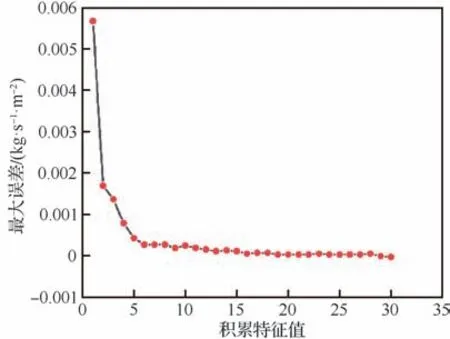
图13 水滴收集量最大误差随积累特征值变化Fig. 13 Maximum error variation of water droplet col⁃lection amount with cumulative eigenvalues

选用9组工况进行验证，具体验证算例工况如表4所示。图14为数值模拟与代理模型水滴收集量对比。图中可以看出无论是水滴收集量的极值还是水滴收集量的分布范围，快速预测结果均与数值模拟结果符合良好，9组算例水滴收集量最大值的平均绝对误差MAE为0.002、均方根误差RMSE为0.003，平均绝对百分比误差MAPE为6.2%，说明所构建的代理模型可以准确地预测翼型表面的水滴收集量。

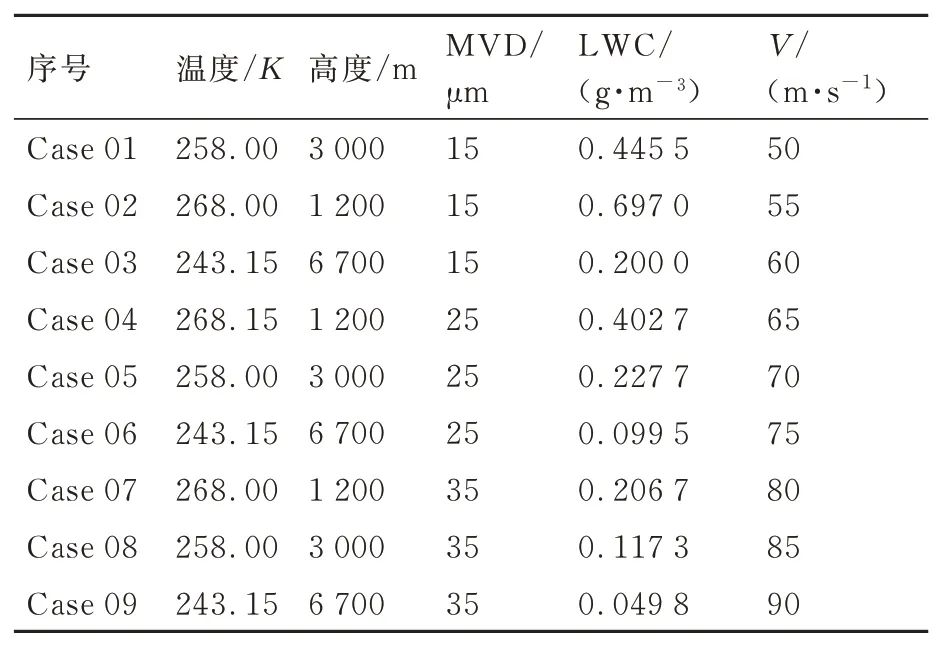
表4 验证工况Table 4 Validation conditions

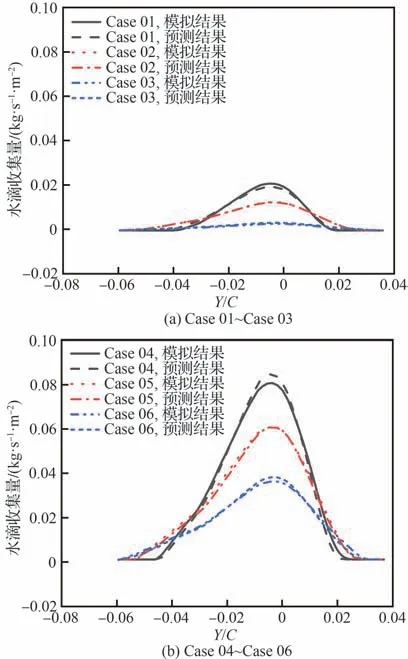
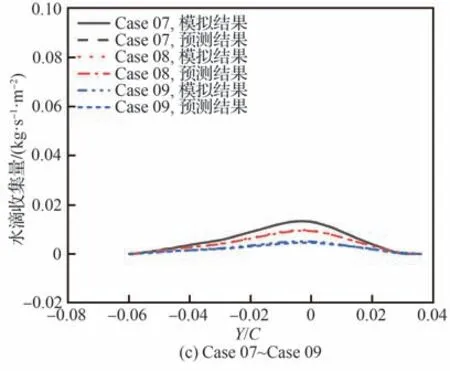
图14 数值模拟与代理模型水滴收集量对比Fig. 14 Comparison of water droplet collection amount between simulations and surrogated models

3.2 结冰气象预测

用WRF模拟了华盛顿山（44.267N，71.3W，海拔1 917 m）2013年4月1日结冰过程。WRF的详细信息可参考2.2节。图7和图8显示了中心点的温度和LWC的比较，结果显示模拟获得的温度与LWC与观测值良好符合。图15为模拟区域和不同高度层的示意图。图16和图17为4月1日6：00时高度层eta=2，4，6的LWC和温度云图。可以看出，LWC和温度在不同层的变化很大。图18和图19分别为6：00、12：00、18：00和24：00时eta=6的LWC云图和温度云图。图中显示LWC和温度在1 d中均发生了很大变化。

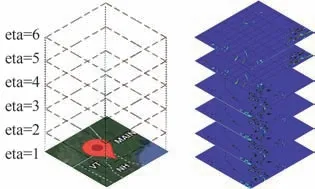
图15 模拟区域及高度层示意图Fig. 15 Schematic diagram of simulated area and height layers

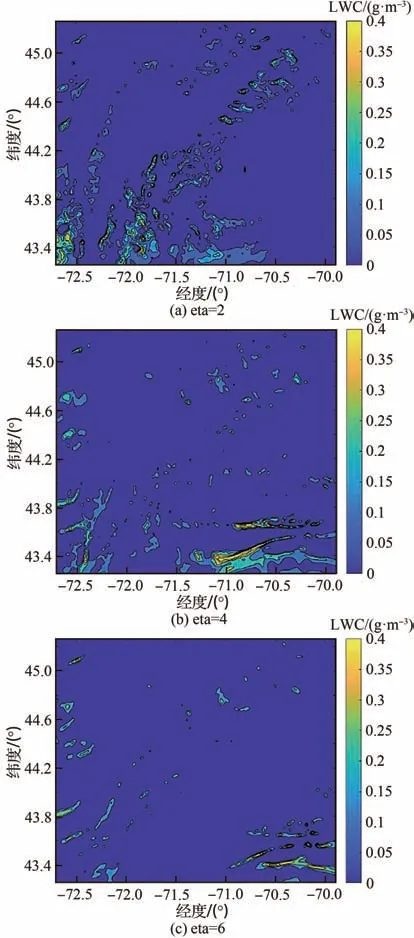
图16 6：00时高度层eta=2，4，6的LWC云图Fig. 16 LWC contours of layers eta=2，4，6 at 6：00

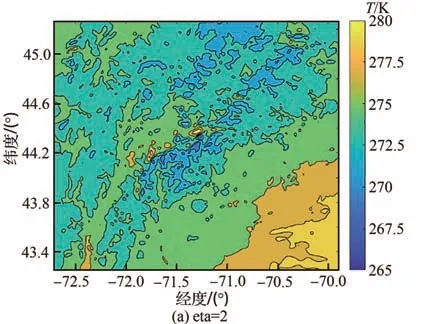
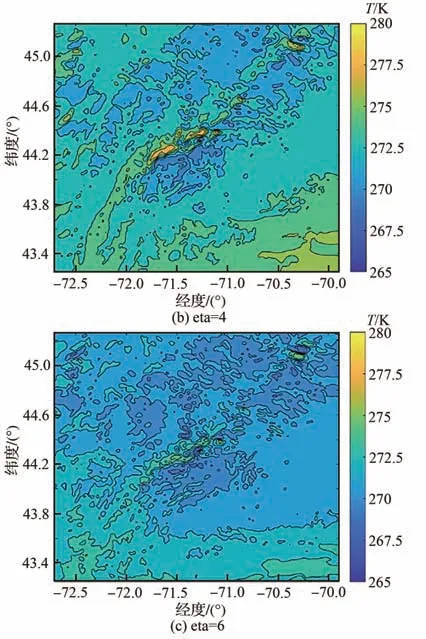
图17 6：00时各高度层eta=2，4，6的温度云图Fig. 17 Temperature contours of layers eta=2，4，6 at 6：00

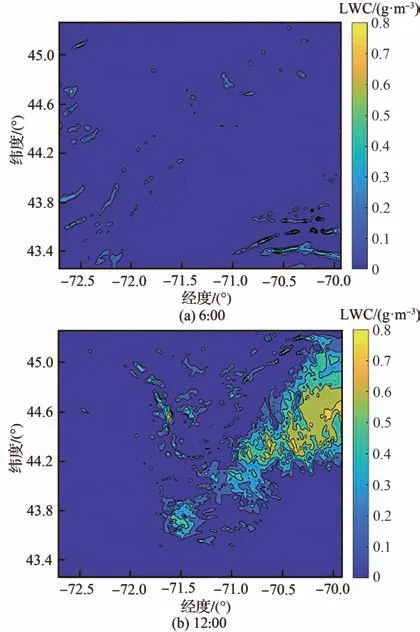
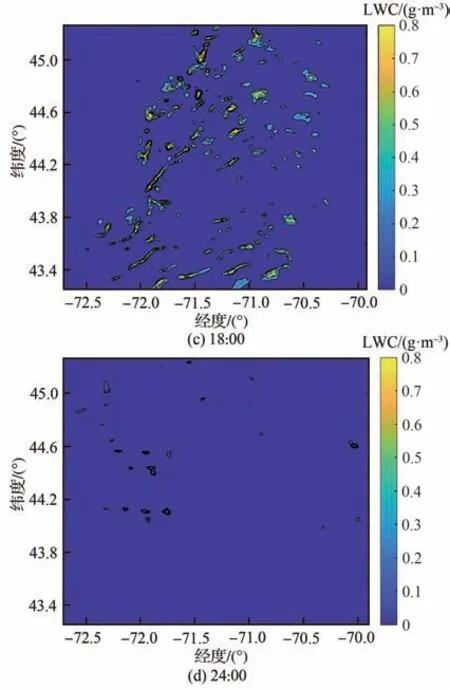
图18 不同时刻下高度层eta=6时LWC云图Fig. 18 LWC contours of layer eta=6 at different time

3.3 结冰试飞空域确定

3.3.1 结冰试飞空域

以WRF气象模拟获得的华盛顿山此次结冰事件中4月1日0：00—24：00时的气象数据为基础，假定飞行速度为50 m/s，利用水滴收集量代理模型对目标区域内的水滴收集量进行快速预测，获得了目标区域内在6：00、12：00、18：00以及24：00时刻下水滴收集量分布。以中度结冰强度对应的水滴收集量为阈值对各个时刻下的空间点进行识别。结冰强度指单位时间内机体表面所形成的冰层的厚度，美国联邦航空条例和航空信息手册将结冰强度划分为4个等级，用以说明结冰情况的严重性。将水滴收集量除以冰的密度即可获得可能的最大增长速率。由于本文主要集中于自然结冰试飞空域的确定，并未考虑结冰过程以及结冰后的形态，在后续的研究中将加入温度对冰增长速率的影响。在本文的研究中，冰的密度取917 kg/m³，且认为冰的密度不变。结冰强度等级见表5［4］。

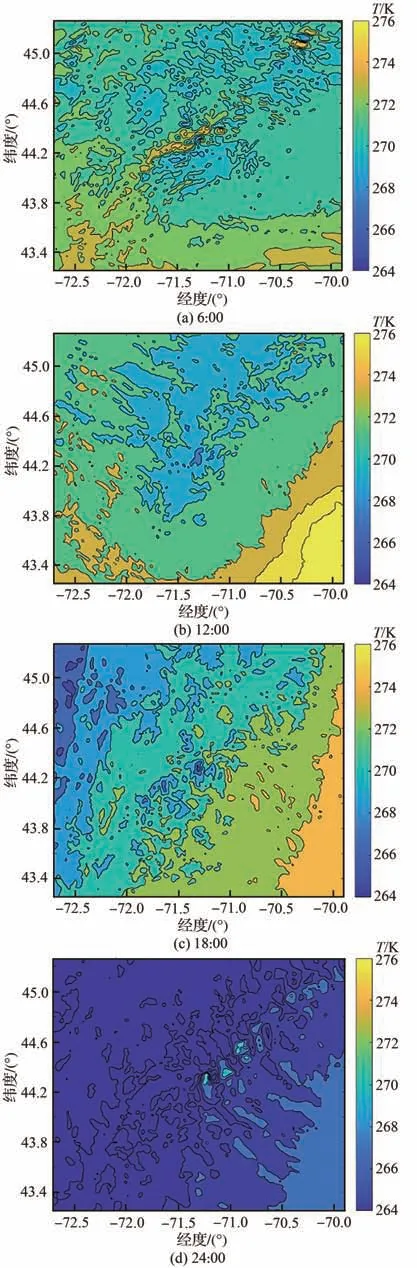
图19 不同时刻下高度层eta=6时温度云图Fig. 19 Temperature contours of layer eta=6 at differ⁃ent time

表5 结冰强度等级［4］Table 5 Icing intensity rating［4］

取中度结冰时水滴收集量0.016 8 kg/（s·m2）作为划分结冰试飞空域的判定标准，认为最大水滴收集量超过该值时，该空域具有结冰试飞气象条件，低于该值时则认为不具有结冰试飞气象条件。对目标区域内的空间点进行筛选，获得不同高度层在6：00、12：00、18：00以及24：00满足条件的点的总数与高度层的曲线图，如图20所示。图中可以看出在6：00、12：00和18：00时刻下均存在结冰试飞气象条件，而在24：00时没有结冰试飞气象条件存在，曲线呈一条直线；不同时刻下满足结冰试飞气象条件的空间点的数量也不相同，满足条件的点数随着高度的增加先增加后减少，在大约高度为2~3 km的范围内达到峰值。图中指出在12：00时刻下eta为5~7时满足结冰试飞气象条件的点数较高。图21和图22为12：00时刻下eta为5~7时的水滴收集量云图和结冰强度云图。图中显示在eta为5~7时存在一个水滴收集量较大的核心区域，如黑色线框所示。在核心区域外，水滴收集量或者结冰强度较低。不同高度的核心区坐标平均高度及平均结冰强度见表6。

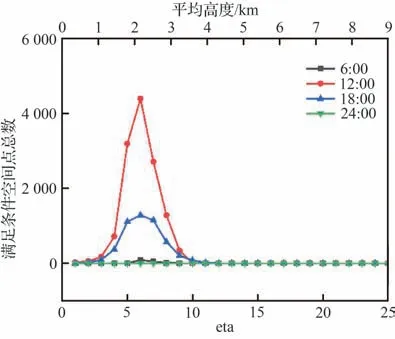
图20 在6：00、12：00、18：00和24：00时满足自然结冰试飞条件的空间点总数随高度层的变化Fig. 20 Variation of total number of points meeting natural icing flight test conditions with height layers at 6：00、12：00、18：00 and 24：00

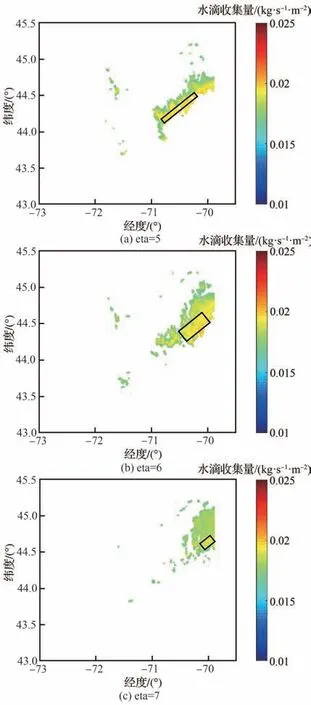
图21 12：00时满足结冰试飞条件的高度层水滴收集量云图Fig. 21 Water droplet collection amount contours of lay⁃ers meeting conditions of icing flight test at 12：00

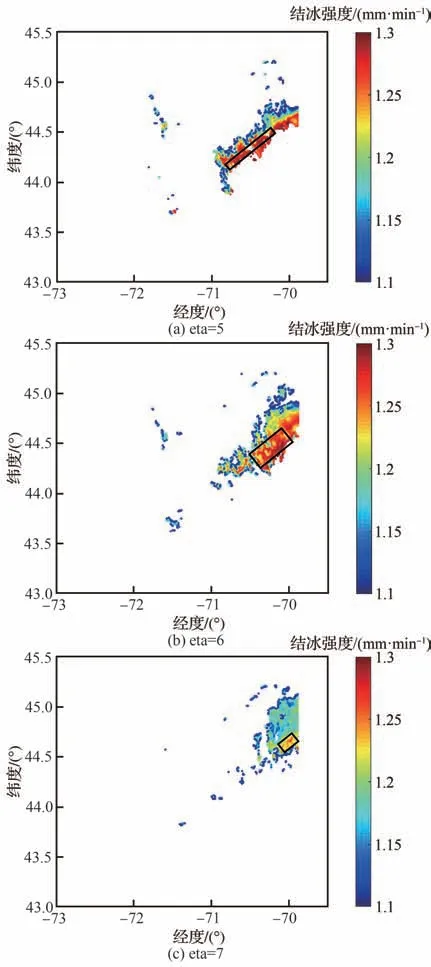
图22 12：00时满足结冰试飞条件的高度层结冰强度云图Fig. 22 Icing intensity contours of layers meeting con⁃ditions of icing flight test at 12：00

3.3.2 飞行速度对自然结冰试飞空域的影响

飞机的结冰受到多种因素的影响，包括气象因素和飞行条件。气象因素中温度、液态水含量以及水滴中值体积直径是不可控因素，而飞行条件中的飞行速度和飞行时间是可以根据需要进行调节的。本文通过对华盛顿山4月1日6：00~24：00时飞行速度为50 m/s和80 m/s时的水滴收集量的变化探究飞行速度对结冰试飞空域选择的影响。

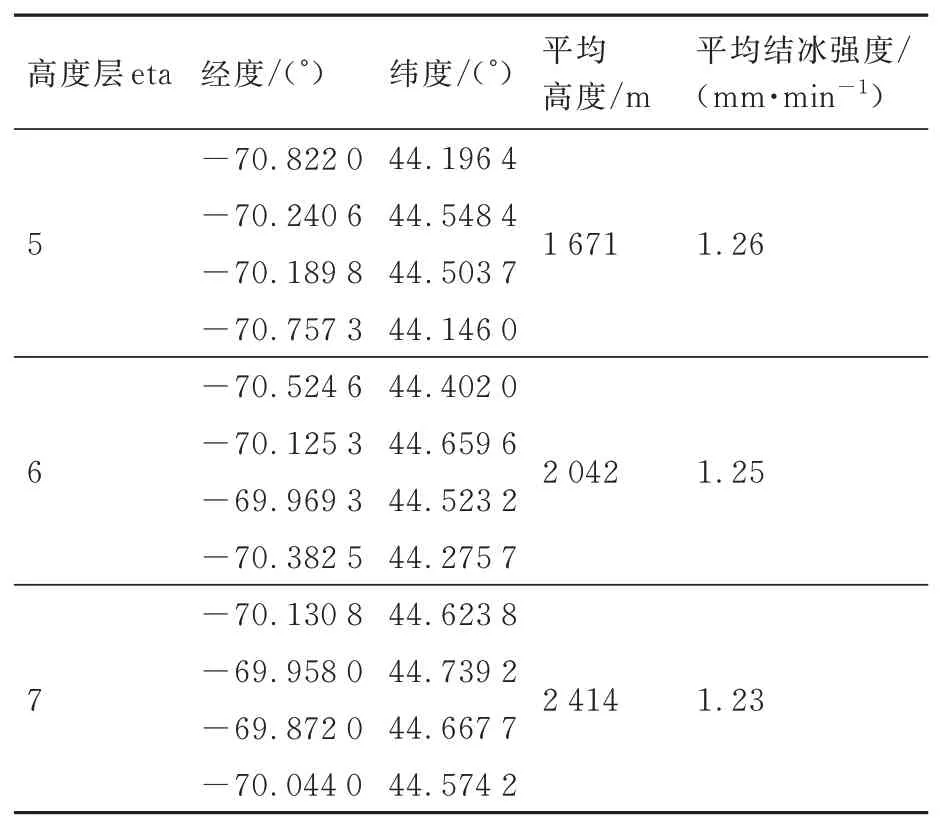
表6 核心区坐标及平均结冰强度Table 6 Core area coordinates and average icing intensity

图23为4月1日6：00、12：00、18：00以及24：00时刻不同高度层满足结冰气象条件的空间点总数对比。图中可以看出对于6：00、12：00、18：00飞行速度为80 m/s时满足结冰气象条件的空间点数相比飞行速度为50 m/s时均有所增加；而在24：00时刻时满足结冰气象条件的空间点数在各个高度层上仍然均为0，说明在24：00时刻时目标区域不具有满足结冰试飞的气象条件。图中也可以看出，在6：00、12：00、18：00时刻下在eta为6时满足结冰试飞气象条件的空间点总数均达到最大值。

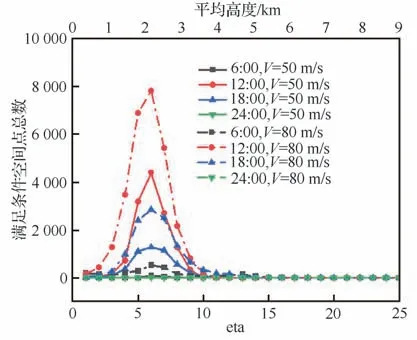
图23 不同速度下满足自然结冰试飞条件的点总数对比Fig. 23 Comparison of total number of points meeting natu⁃ral icing flight test conditions at different speeds

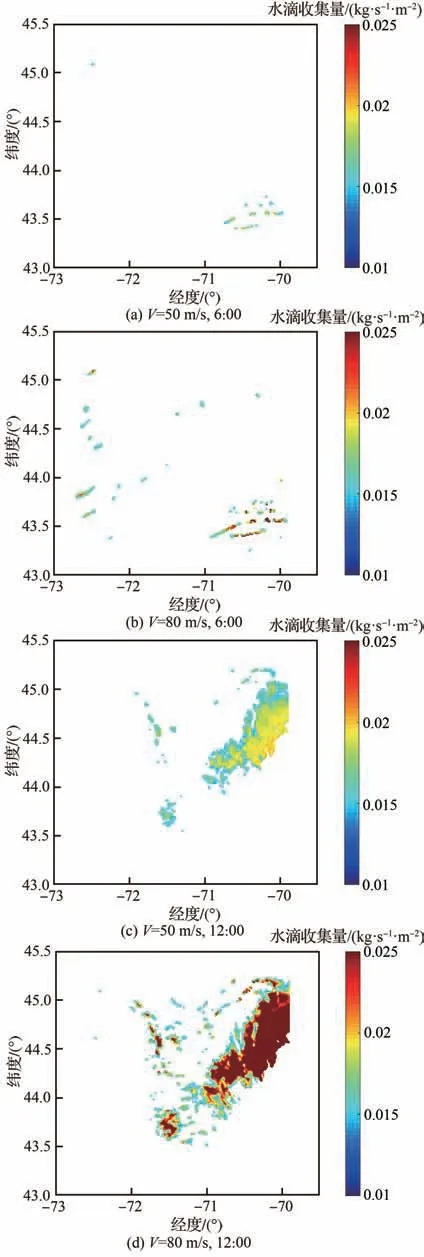
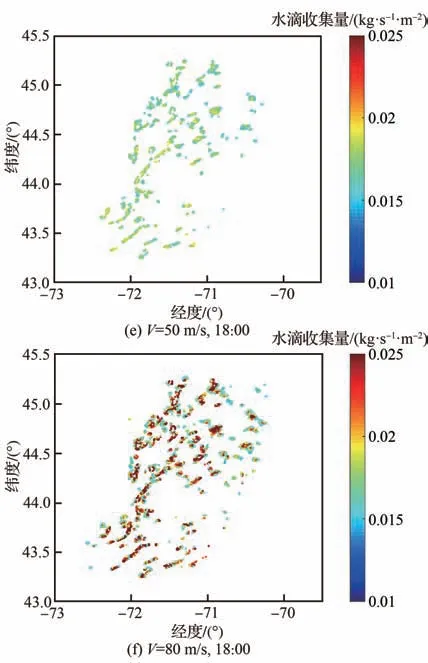
图24 不同速度下高度层eta=6时水滴收集量云图对比Fig. 24 Comparison of water droplet collection amount contours at different speeds of layer eta=6

图24为eta为6时6：00、12：00、18：00下速度为50 m/s和80 m/s时满足结冰试飞气象条件的空间点分布。图中可以看出由于速度的增加，目标区域中满足结冰试飞气象条件的空间点均有所增加，在速度为50 m/s情况下目标区域不具有结冰气象条件的点，在速度为80 m/s的情况下出现了满足结冰试飞气象条件的点，如图24（b）所示。此外，由于速度的增加，导致水滴收集量在一些区域内过大，如图24（b）、图24（d）以及图24（f）中的深色区域，这些区域内的结冰强度可能达到严重结冰，若在这些区域内进行结冰试飞，可能导致事故发生。

4 结 论

1） 通过POD降阶模型和Kriging插值方法构建了水滴收集量的代理模型，代理模型可以快速预测结冰气象参数（温度、LWC、MVD）和飞行参数（速度、高度）对水滴收集量分布的影响；将水滴收集量等效转换为结冰强度，作为试飞空域确定的划分依据。

2） 通过WRF模式对2013年4月1日华盛顿山处一次结冰事件的气象预测，获得目标区域内结冰气象条件；基于水滴收集量的代理模型快速获得目标区域内水滴收集量分布，利用试飞空域划分依据获得了适合结冰试飞的空域、时间以及结冰强度。

3） 对速度对自然结冰试飞区域的影响进行研究，发现速度的增加使得水滴收集量增加，进而使得原本没有结冰试飞气象条件的位置出现了满足结冰试飞的条件，也可能导致原本满足结冰试飞条件的位置水滴收集量过大从而威胁飞行安全。