基于材料基因工程方法的固态锂离子导体材料快速搜索研究
税 烺 ,付建辉
(1.成都先进金属材料产业技术研究院股份有限公司特钢技术研究所,四川 成都 610303;2.海洋装备用金属材料及其应用国家重点实验室,辽宁 鞍山 114009)
0 引言
材料是人类社会发展的重要物质基础,新材料技术是体现一个国家科技发展水平的重要指标之一。近年来,传统材料科学研究中依赖科学直觉与重复试错的研究方法已逐渐跟不上技术快速发展的需求,成为限制材料科学发展的瓶颈。2011 年6 月,美国政府提出了“材料基因组计划”(Material Genome Initiative),其目的是利用材料模拟计算、高通量实验和数据挖掘等技术将材料从发现到应用的速度至少提高一倍,成本至少降低一半[1]。材料大数据挖掘技术是材料基因组计划的一个重要组成部分,其包括聚类分析、预测模型、关联分析、异常检测等方法,对海量材料数据进行挖掘,快速寻找材料“工艺-成分-结构-性能”之间的内在规律,从而建立起数据驱动的材料计算模型,以期最终实现材料的“按需设计”。
锂离子电池(LIBs)多年来在各类型电子器件中得到了广泛的应用,其中特别是在移动电话和电动汽车领域[2]。目前常见的锂离子电池基本都使用液态的电解质,这类电解质通常是溶解有锂盐的有机溶剂。因为具有低成本和高锂离子电导率的优点,使用这类电解质的锂离子电池通常具有较高的输出功率。但是,有机溶剂非常容易产生安全性和稳定性的问题,例如,当电池遭受机械损伤或短路时,有机溶剂容易起火燃烧,电解质与电极反应导致电池总体输出功率衰减,以及外部热源易使有机溶剂蒸发导致电池内压增大最终产生爆炸等[3]。相反的,固态锂离子电池使用固态的电解质代替有机溶剂电解质,因而在可提高阴极电压的同时抑制电极反应发生,减轻电池起火和爆炸的风险,并且可以防止电极上的枝晶生长。由于其安全性、稳定性和高能量密度的特点,固态电解质锂离子电池在未来有望代替液态电解质锂离子电池[4−5]。尽管如此,当前固态电解质面临的主要问题是其离子电导率相较于液态电解质低多个数量级[6]。材料研究学者在多年以前已经开始高离子电导率的固态材料的搜寻工作,到目前为止,文献中已报道了数种在室温下离子导电性接近于液态电解质的材料[7−8]。除此之外,一种可以作为商用固态电解质使用的材料还需要具备化学稳定性、低电子电导率、低成本等特点,因此,对于可广泛使用的高离子电导率固态电解质的搜寻条件变得更加苛刻。
传统的搜索方法是“试错法”,研究人员试图逐一合成可能的高离子电导率化合物[9]。然而,由于已知的含锂固体化合物有数万种,这种方法的效率相对较低。近年来,“高通量计算”的概念得到推广,通过高通量计算筛选候选化合物已成为寻找理想固体电解质的一种新方法[10]。2014 年,Gao 建立了基于键价模型的筛选模型,并用该模型筛选了ICDD 2004 材料数据库。该研究者首先设置了排除稀有或环境污染元素和变价元素化合物的前置条件,将候选化合物的数量从 109 846 减少到 1 380。然后,该研究者构建了键价模型,筛选出 1 380 个候选物来预测每一种材料的锂离子电导率[11]。Sendek 遵循类似的筛选程序从 Material Project 数据库筛选化合物数据。Sendek 首先设置了筛选前置条件,将可能的候选材料从12 000 多个减少到300 个左右,前置条件包括电子电导率、结构稳定性、成本、地球丰度等。后来,该作者使用了 40 种晶体结构和在文献中已报道的实验测量的离子电导率值来建立逻辑回归模型,然后使用训练好的机器学习模型筛选选定的 300 种化合物,以期找到有应用前景的高离子电导率化合物[12]。该模型基于实验获得的数据不涉及传统的 DFT 计算,因此是真正的“数据驱动”计算。2018 年,Zhai 在搜索高居里温度钙钛矿材料时应用了类似的“数据驱动”方法。该作者从参考文献中收集了 47 个数据并建立了机器学习模型,然后将其用于预测候选材料的居里温度[13]。
笔者以相关材料数据较多的固态锂离子导体材料为研究对象,建立起数据驱动的筛选模型,并评估其模型复杂度、预测精确度、材料筛选结果以及模型误差来源。该研究方法属于材料基因工程的典型研究方法,对其它类型的新材料的设计、筛选和优化也具有指导意义。
1 模型建立
在本研究中,我们使用包含 20 个从晶格参数计算并与离子电导率相关的特征空间来构建机器学习模型[11]。训练数据集包含 46 种含锂化合物,其中包括从文献和Material Project 数据库中收集的晶格参数和电导率。首先,我们将 Sendek 提出的筛选前置条件应用于 Material Project 数据库中的所有含锂化合物,将候选化合物从 10 000 多个减少到 343 个。前置条件基于电子电导率、结构稳定性、稳定性阴极氧化,锂金属阳极还原稳定性,排除了不适合商业应用的电解质化合物。之后,使用机器学习算法建立筛选模型,然后使用经过良好训练和验证的模型筛选上述选出的 343 种候选材料,判断其是否为超离子导体材料。
包含 46 种材料和 20 个特征值的训练数据集展示在附件表 S1(详见OSID 码内增强出版内容) 所示。其中,这20 个材料特征是依据Sendek 所提出的与锂离子电导率密切相关的特征,是由材料晶格参数计算而来[11]。表的最后一列是每个样本的分类标签,它是一个布尔变量,表示化合物是否为超离子导体化合物。由于不同化合物的电导率通常在很大的范围内变化,为了减少模型的拟合误差,通常使用布尔变量来限制变化范围,因此模型构建时不使用真实的电导率数值。在本模型中,将离子电导率σ ≥ 10−4S/cm 的材料视为超离子导体,而 σ <10−4S/cm 的材料视为非超离子导体材料,分别对应于=1 和 0。
1.1 决策树和随机森林模型
根据含锂化合物的许多物理特征来判断其是否为超离子材料是一个典型的二元分类问题,决策树是一个适合解决该问题的算法。一个训练好的决策树在每一步中通过一个选定的特征将数据集分类为多个子数据集并迭代该过程,因此子数据集被不断分类为下一级的子数据集,直到每个子数据集中的数据是相同的标签或满足其他预设条件。决策树算法的数学基础是将特征空间划分为样本标签相同的单元或区域。图1 显示了特征空间划分的示例。图1 中的特征空间由两个特征组成,这使得特征空间成为一个平面。将平面分成两个区域的线将正样本和负样本分开,所以这四条线代表了一个分类模型,对应于一个训练好的决策树。包含m个特征的问题即是在m维的特征空间中寻找到这样的分类模型[14]。

图1 二维特征空间划分示意Fig.1 Schematic diagram of a 2D feature space division
在本研究中,含锂材料的特征空间是 [AAV,SDLC,SDLI ...RNC],是一个 20 维的空间,如附件表S1 所示。基于已知数据的分类方案应该建立在这个 20 维的特征空间上。根据决策树算法,需要逐步决定选择20 个特征中的哪个特征作为分类节点,并确定其值是多少。文献中常用的有ID3、C4.5 和CART 三种树生成算法。这三者中,ID3 算法对训练数据集采用“信息增益”来确定选择哪个特征及其分类值,而 C4.5 算法采用“信息增益比”,CART采用 Gini 系数[15]。在本研究的问题中,分类模型的预期输出是一个布尔变量(0 或1),即一个二元分类问题。因此,采用计算成本较低的输出为二叉分类树的CART 算法进行模型构建。
1.1.1 Gini 系数
在 CART 算法中,Gini 系数表示从数据集D中随机抽取的两个样本其标签不同的概率。因此,较小的 Gini(D)表示数据集D的纯度较高。集合D上的 Gini 系数定义如下:

其中D表示数据集;pk表示D中第k个标签的样本所占的概率;k表示样本标签的序列号;|y|表示标签类别的总数。在划分数据集时,选择划分数据集的最佳特征应该使所有子集的加权基尼指数之和最小,因为Gini 系数最小表示集合纯度最高。因此,集合D上某个特征A的 Gini 系数定义为
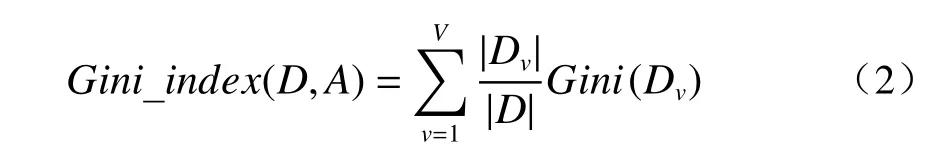
其中V表示使用特征A划分集合D生成的子集的总数;Dv表示第v个子集;|Dv|和|D|分别表示子集Dv和集合D中的样本数。在二分类的情况下,样本只有两个标签,所以|y|等于2,故D中标签k和k'的概率简化为

因此式(1)可以简化为

因此,每次划分只生成两个子集,所以有V=2,式(2)简化为
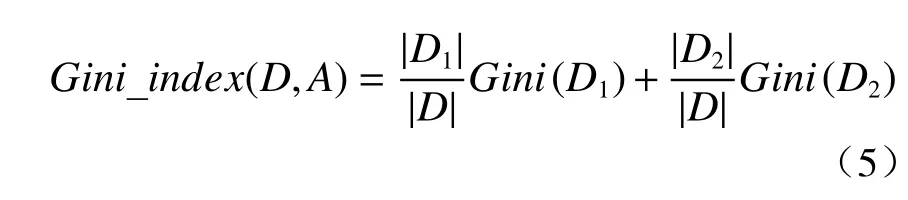
通过计算每个特征的Gini 系数,可以寻找到最小的Gini 系数,其对应的特征是当前步骤划分数据集的最佳特征。
1.1.2 连续数值的划分
如附件中表 S1 所示,每个特征的值是一个连续的数字,而不是离散的。为了处理这些连续的特征值,首先将每个特征的所有可能值从小到大排序,形成一个集合[a1,a2,a3…at],其中aj(1≤j≤t) 表示任何可能的某个特征的取值,并且a1≤a2≤a3≤···≤at。其次,相邻两个值的中间值dj可以表示为

然后将dj用作分割值。因此,通过式(6),对于具有t个可能值的某个特征,有t−1 个划分值[d1,d2,d3···dt−1] 将数据集D划分为左集和右集。左集由对应特征值小于或等于分割值的样本组成,而右集则由大于该分割值的样本组成。因此,对于每个具有t个可能值的特征,都有t−1 种划分方式。对于每一种划分方式,都有一个对应的基尼指数。某个特征的最佳划分值是使相应的基尼指数最小的那个。
1.1.3 简单决策树模型
根据式(5)和式(6),计算出每个特征的最佳划分值和对应的Gini 系数,选择20 个特征中Gini 系数最小的特征作为划分数据集的最佳划分特征。通过迭代这个过程,对前一次划分产生的子集进行逐次划分,最终在附件表S1 的数据集上生成一棵二分类树,如图2 所示。该树的每个节点的特征代表它是当前步用于分割的特征,该值表示该特征的最佳分割值,其中节点下的左分支表示值小于或等于分割值的样本,右分支表示大于该分割值的样本。每个特征都可以重复用于划分子集。树的叶节点表示该子集内样本的标签是相同的,其中 1 表示超离子导体,0 表示非超离子导体。由于数据集仅包含46 个样本,因此很难分为训练集和测试集。因此,此简单决策树模型使用整个数据集训练决策树,并通过留一法(LOO)方法估计预测的泛化精度,可以使用以下公式计算准确率:
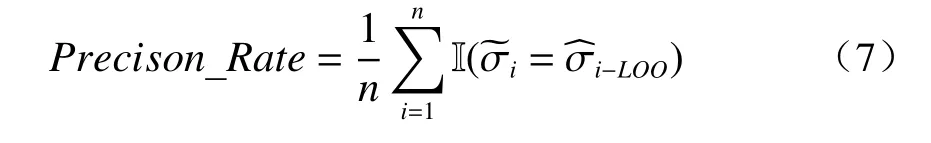
其中n表示样本总数;表示表S1 中每种材料的标签,1 和0 分别表示超离子和非超离子导体,表示由当前模型使用 Leave-One-Out 方法预测的每种材料的标签,I (X)表示一个指示函数,如果X为真则返回 1,如果X为假则返回 0。训练好的决策树如图2 所示。这棵树在训练集上的准确率为 1.0,通过 Leave-One-Out 方法计算得到的泛化准确率为0.804 3。通常,训练集上的准确率接近 1.0 表明模型过拟合,泛化能力通常有限。因此,应该对该简单决策树模型进行修剪以提高其泛化能力。

图2 决策树1:采用整个数据集训练,未剪枝Fig.2 Decision tree 1:trained by the entire data set with no pruning
1.1.4 剪枝后的决策树
图2 中的决策树是基于整个数据集训练而得到,没有其他预设条件,因此其在训练集上计算达到了最优化的结果,使训练集的准确率达到 1.0。为了避免这种过度拟合,应该简化树并降低训练集的准确率,同时提高其泛化的准确率。本研究提出一个剪枝方案:
1) 将数据集拆分为训练集和验证集,并保证两组中正样本的比例几乎等于整个数据集,其中验证集的样本数设置为9,约为样本的1/5 整个数据集。
2)使用训练集中的样本训练一棵树。
3)用叶节点替换训练树中最低的非叶节点,并将叶节点的标签指定为与该节点对应的训练样本中出现最多的标签。
4) 计算替换树的准确率,如果替换树的准确率不低于原树,则执行节点替换。
5) 迭代第3 步和第4 步,直到没有最低的非叶节点满足第4 步的剪枝条件,输出剪枝后的树。
6) 剪枝树的泛化准确率在训练集上采用 Leave-One-Out 法计算,代表了上述剪枝策略的泛化能力。
上述剪枝方案生成图3 中的决策树,其中Leave-One-Out 方法的泛化准确率为0.810 8。如图3 所示,即使对树进行了剪枝,仍然有一些特征被重复选择为划分节点,例如 PF 和 SPF,而其他特征没有在Gini 指数比较中被选择用于划分。由于数据集的大小有限,某个特征如PF 和 SPF 的重要性被放大,表明剪枝后的决策树模型存在局部最优的迹象。因此,需要一种提供更好泛化能力的方案。

图3 决策树2:使用训练集数据训练并使用验证集数据剪枝Fig.3 Decision tree 2: trained by samples in train set and pruned by samples in validation set
1.1.5 随机森林
随机森林是一种基于决策树的集成算法。通常,在分类问题中,随机森林生成一组决策树,并输出所有树输出的简单多数票结果,工作流程如图4 所示。由于引入了几种随机操作,随机森林通常具有更好的避免局部最优的能力[16−17]。这里我们设计模型构建的方案如下:

图4 一个包含M 棵决策树的随机森林模型工作过程示意Fig.4 Schematic working flow of a random forest with M trees
1)通过从原始数据集中随机抽取样本来创建原始数据集相同大小的bootstrap 集,其中原数据集中的一些样本可能被多次抽取而一些未被抽取。
2)使用bootstrap 集来训练决策树,方案如下:在树的每个节点,从所有20 个特征中随机抽取一个特征子集;这里子集的大小预设为 log220 ≈ 4;然后通过对子集中特征的基尼指数比较而不是在所有20 个特征中选择当前节点处的最佳分割特征。
3) 重复步骤 1 和 2,直到树的数量达到预设的最大值。
4)随机森林的泛化准确率通过Out-Of-Bag 精度计算:将数据集中的每个样本都带入训练好的森林中测试输出,其中只使用森林中那些bootstrap 集不包含该样本的树进行简单多数投票。
如图5 所示,随机森林的准确率随着森林大小的增加而增加,最终达到 0.782 6 的稳定水平。为了平衡精度和计算成本,200 棵树的数量对于当前数据集来说是足够的森林大小。由于随机森林集合了许多决策树,它的输出在很大程度上降低了陷入局部最优的概率。因此,在这种情况下,随机森林模型比上述两种决策树模型具有更好的泛化能力。
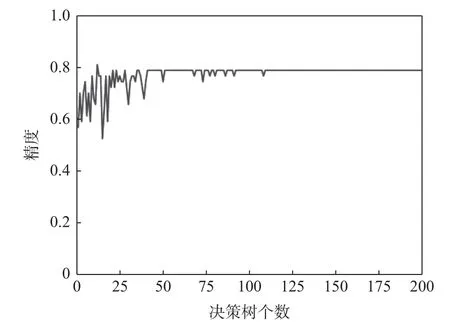
图5 随机森林的预测精度随决策树的个数的变化过程Fig.5 Precision rate of random forest vs.number of trees in the forest
1.2 逻辑回归模型
为了与上述模型进行比较,还构建了一个文献较常使用的逻辑回归模型,使用相同的数据集进行对比。逻辑回归是一种二元分类模型,基本表达式如下:

其中yi表示样本被分类为正样本的概率。具体来说,这里它表示化合物被归类为超离子导体的概率。xi是给定样本i的特征矩阵。

ωi是当前样本i的线性回归的参数矩阵,其中每一项θi依次对应特征矩阵中的一个特征。b代表线性回归中的常数。

逻辑回归模型的输出是给定材料是超离子导体的概率。为简单起见,将y>0.5 的材料视为超离子材料。
由于我们不知道这 20 个特征中有多少与材料的离子电导率密切相关,因此将在数据集上测试 20个特征的所有可能组合,可能组合的总数为。同时将计算数据集上的误分类率来评估每个组合,并选择误分类率最小的组合作为最终模型。为了测试每个组合,需要穷举搜索过程。图6 显示了误分类率随所选特征数数量的变化。结果表明,当特征数数量为 5、6、7、8、9 和 10 时,误分类率达到最低点。考虑到最简单的模型,具有5 个特征数的模型是最佳选择。在这种情况下,五特征模型的线性回归部分为:

图6 误分类率随特征数的变化Fig.6 Miss classification rate vs.number of features
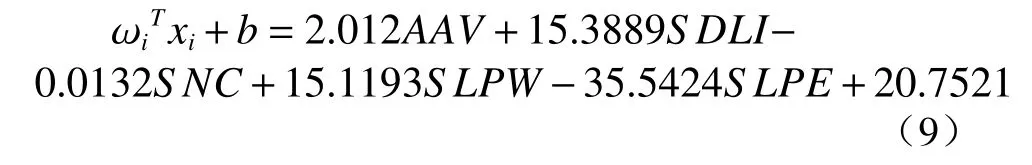
其中误分类率为0.043 5。
2 结果与讨论
2.1 算法复杂度
随机森林的复杂度为 O(M(nlog2(m+n)),其中M表示森林中的树数,n表示用于训练的样本数,m表示特征数。这样的复杂度是相对节省时间的,特别是当树数M没有达到太大的值时。因此,随机森林是一种适用于材料筛选中预测模型构建的算法,尽管它的时间成本比简单的决策树模型要大。相比之下,Logistic 回归模型需要特征选择,因为每个特征与离子电导率的相关性不明确,因此必须进行穷举搜索,因为要检查特征组合的每个组合。因此,特征组合穷举搜索的逻辑回归复杂度为其中n表示用于训练的样本数,m表示特征数。在本研究中,当m=20 时,结果为,即1 048 575。本研究中的实际计算时间成本尚可接受。然而,随着相关研究的继续,特征和训练样本的数量可能会显著增加,从而导致计算时间成本的明显上升。因此,在未来的研究中,采用穷举搜索来处理特征选择的方法可能会受到限制。
2.2 筛选结果
随机森林和逻辑回归的筛选结果如表1 所示。两种模型预测的正样本材料总数均为42 个,占343个候选材料的12.24%。此外,图2 和图3 两种决策树模型的筛选结果见附件表 S2。由于随机森林模型基于决策树的多个基学习器,因此其预测更加稳定可靠。在随机森林的筛选结果中,值得注意的是Li2GePbS4被标记为超离子材料[4]。它是文献中报道的基于阴离子包筛选得到的典型硫化物,并且在Sendek 的逻辑回归筛选中也被预测为超离子导体候选材料,这是对当前模型预测的一个验证。另一种值得注意的超离子材料是 Li9Er3Cl18,它与 Li3In-Br6-xClx(0 表1 随机森林模型与逻辑回归模筛选结果对比Table 1 Screening results comparison of the random forest model and logistic regression model 当前随机森林模型、逻辑回归模型的筛选结果共有13 个共同材料。两个模型均预测了共42 种超离子材料,共同率为30.95%。目前的随机森林模型和逻辑回归模型都是用同一个小数据集训练的,因此不同的机器学习模型可以从中学习到很多共同的但无法进行泛化的分类规则。因此,当这些训练好的模型用于筛选未知样本时,很难判断一个被预测为正样本的材料是由于模型训练集小还是由于该材料内在属性所导致的。因此,有限数量的训练样本可能导致模型泛化能力低,这是误差的主要来源。其次,筛选结果中的许多材料是多阴离子的。多阴离子材料的预测置信度可能会受到计算特征 AFC和 LASD 对阴离子定义不明确的影响,因为这两个值取决于晶格中阴离子的定义方式。通常,我们使用电负性最大的原子进行计算而忽略其他阴离子,这可能会导致特征 AFC 和 LASD 的值不准确。更精确的 AFC 和 LASD 计算策略或构建优化的特征空间,例如增加或减少特征数量或直接使用原子参数作为特征,可能是在未来研究中改进模型构建的适用方法。 在本研究中,我们使用从已发表论文搜集的数据和从原子参数计算的 20 个特征组成的数据集来构建决策树和随机森林模型以及逻辑回归模型进行比较。简单的决策树模型训练准确率很高,但交叉验证准确率相对较低,说明模型过拟合,泛化能力低。修剪后的决策树模型具有更好的泛化能力,但由于训练集的大小较小,某个特征的重要性被放大,表明模型处于局部最优状态。随机森林模型是一种基于决策树的集成机器学习模型。模型构建过程采用随机抽样创建bootstrap 集和随机特征选择策略,避免陷入局部最优,模型表现出较好的泛化能力。随机森林的复杂度为O(M(nlog2(m+n)),适用于更高维度的特征空间和更大的训练集。相比之下,特征组合穷举搜索的逻辑回归模型复杂度为其对于当前数据集和特征空间的大小是可以接受的,但可以预见的是,对于未来更大的数据集和特征空间其计算过程复杂度太高。 本研究构建的随机森林模型的筛选结果将超离子导体候选材料的数量从343 个减少到42 个,排除了87.76%的材料,这在很大程度上缩小了搜索范围。随机森林模型的结果与文献中报道的筛选结果有部分共同材料。一般来说,Li2GePbS4是一种已证明的超离子导体化合物,而 Li9Er3Cl18具有与报道的快速离子导体 Li3InBr6-xClx(0 现有模型的主要误差来源是训练数据集规模小,机器学习模型可能从中学习到一些仅适用于当前数据集且不可泛化的分类规则,最终预测未知数据的精度受到影响。另一个错误来源是特征的定义及其计算过程,因为在计算某些特征值时进行了一些简化。为了考虑误差源,构建优化的特征空间,例如增加或减少特征数量或直接使用原子参数作为特征,可能是一种适用的方法。 附:数据可用性 重现本文中的模型所需的数据可以在本文的补充文件中找到,详见OSID 码内增强出版内容。
2.3 模型分析及误差来源
3 结论

