基于人工免疫的渐消容积粒子滤波目标跟踪算法

张铠翔 姜文刚

(江苏科技大学电子信息学院 江苏 镇江 212000)

0 引 言

目标跟踪技术作为环境感知的核心技术之一，在军事勘察、精确制导、安防监控等领域都有着巨大的应用前景。由于目标跟踪的整个过程存在各种噪声，所以几乎都是对非线性的状态估计。针对非线性或者非高斯系统的状态估计问题，目前的解决方法有扩展卡尔曼滤波[1](Extended Kalman Fifilter,EKF)、无迹卡尔曼滤波[2](Unstend Kalman Fifilter，UKF)、容积卡尔曼滤波[3](CubatureKalman Fifilter，CKF)、粒子滤波[4](Particle Fifilter，PF)等经典非线性算法。

其中粒子滤波算法是贝叶斯估计理论的一种非线性算法，且相对于其他算法在目标跟踪领域更具有优势。然而传统的粒子滤波并没有考虑最新观测，这便导致重要性采样过程得出的样本与真实分布存在较大的偏差，以及重采样阶段也会随着不断的迭代过程导致粒子匮乏，丢失了粒子的多样性，进而使状态的估计精度下降[5]。针对粒子滤波存在的退化问题，近年来不断有学者提出解决方法。文献[6]通过迭代扩展卡尔曼和粒子滤波进行融合改进粒子滤波的重要性密度函数。文献[7]为了缓解粒子退化和提高系统预测精度，提出基于强跟踪无迹卡尔曼滤波算法，其中将强跟踪无迹卡尔曼预测的状态分布作为重要性密度函数。文献[8]则使用差分演化算法与容积粒子滤波融合，由容积卡尔曼滤波产生重要性密度函数，可以进一步优化粒子，提高滤波的预测精度。这三种算法都充分考虑了当前的观测值，进一步优化了重要性密度函数，但对于重采样过程中粒子多样性丢失的问题并没有很好地解决。

本文基于容积粒子滤波(Cubature Particle Fifilter,CPF)在提议分布和重采样这两点上进行改进：(1) 引入文献[9]中的渐消滤波与容积粒子滤波相融合产生自适应提议分布函数，使得融合的提议分布更加逼近真实状态，进而缓解粒子退化；(2) 在重采样过程中引入基于人工免疫[10]的重采样并进行自适应部分重采样。通过这两点可以有效地提高粒子的滤波能力，可以有效地缓解粒子的样本退化和贫化。

1 容积粒子滤波算法(CPF)

1.1 容积卡尔曼滤波(CKF)

假定非线性系统模型离散系统：

xk+1=f(xk)+w(xk)

(1)

zk+1=h(xk)+v(xk)

(2)

式中：xk、zk分别为状态值和观测量；w、v分别是过程噪声和测量噪声；f与h分别为非线性系统的状态转移函数和量测函数。

CKF算法主要是利用球面径向原则来进行高阶积分。容积的原则主要是通过点集进行非线性传递，然后通过加权求和来近似于非线性函数的后验均值和方差。

进行容积规则与高斯分布结合：

(3)

式中：N为高斯概率密度；I为协方差。

容积点个数为：

m=2n

(4)

式中：n是状态维数。

权重大小为：

(5)

容积点为：

(6)

式中：[1]为完全对称的点集。

在高维度中CKF相比于UKF、EKF具有更好的收敛性和滤波精度。

1.2 基于自适应渐消容积粒子滤波(CPF)

CPF是通过CKF来改进粒子滤波算法的。主要是在粒子滤波的重要性采样的过程中通过CKF来计算每个粒子的均值和协方差，然后就是通过得到的均值与协方差来进行提议采样。由于在使用CKF计算均值和方差可以更好地来逼近后验概率密度函数，也就是融合了最新的观测值Zk。

容积粒子滤波算法具体过程如下：

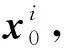
(7)

(2) 重要性采样阶段。当k=2,3,…，通过CKF进行计算每个粒子的下一时刻的均值和协方差，分别进行时间更新和量测更新。

时间更新：

第一步：对容积点进行计算：

(8)

(9)

第二步：传播容积点：

(10)

第三步：下一步的状态预测值和协方差预测值：

(11)

式中：R为过程噪声。

量测更新：

第四步：对下一步的状态预测值求解容积点：

(12)

(13)

第五步：容积点传播：

(14)

第六步：进行测量预测值的计算：

(15)

第七步：进行测量误差的协方差和测量误差与状态误差的互方差计算：

(16)

第八步：增益更新:

(17)

第九步：融入当前观测值的预测状态值和测量协方差：

(18)

(19)

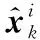
(20)

(3) 计算粒子权重并归一化处理：

(21)

归一化权重：

(22)

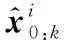
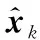
(23)

(24)

2 自适应渐消容积粒子滤波(AFCPF)

由于CPF是通过CKF来进行重要性采样的，在这个过程中由于CKF是通过确定点进行采样的，在实际运用的过程中会出现系统初始化建模不准确的问题[11]。UPF也存在类似问题，文献[12]将渐消滤波与UPF结合来应对系统模型匹配不准确时，可以通过渐消因子进行在线调整变益矩阵，从而使建议分布更加逼近真实分布。为了解决CPF出现这类情况，本文将渐消因子与CPF进行结合。结合过程如下。

(25)

α0,k=tr(Nk)tr(Mk)-1

(26)

式中：tr()为求迹公式。Nk、Mk在CPF中的公式如下：

(27)

(28)

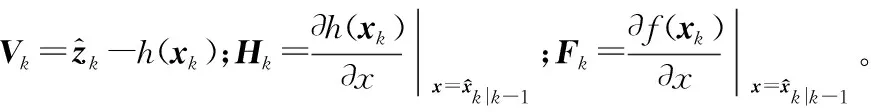
则将渐消因子融入式(19)后新的测量协方差计算公式为:

(29)

通过渐消因子αt对增益矩阵进行在线调节从而使得每个粒子的协方差可以自适应地调节，进一步地获得更加可靠的观测信息，对干扰状态模型和观测模型的不利因子进行抑制，这样可以有效地使提议分布更加逼近真实的状态分布。

3 自适应部分人工免疫重采样

3.1 人工免疫(AAI)重采样

人工免疫算法[13]主要构架思想是起源于生物免疫系统，通过人为的形式来对模仿生物进化选择机理，其实是优胜劣汰的一种思想。利用细胞智能群体进行寻优，实现系统的全局最优解的迭代过程[14]。研究证明人工免疫群算法是通过对抗体的克隆和变异产生新的抗体，可以很好保证了样本的多样性，以及产生满足要求的最优解的时间较短，相比于其他群智能算法具有更高的收敛速度。

本文基于人工免疫重采样的AFCPF具体步骤如下：

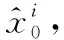
2) 重要性采样。得到具有不同权重的抗体集合。并进行归一化处理，将N个新的抗体存入抗体记忆序列。

3) 设定重采样阈值。

(30)

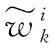
4) 计算抗体亲和力。抗体的亲和力表示抗体与抗原之间的匹配度。抗体的亲和力越高，说明抗体与抗原匹配度越低。也就是亲和力度与匹配度成反比。

则设定抗体i在k时刻的亲和力计算公式如下：

(31)

5) 抗体间互斥力计算。粒子间的距离作为衡量粒子间互斥力的大小。取任意第i个抗体与第j个抗体在k时刻的互斥力。

(32)

6) 进行抗体克隆。抗体的克隆数目以抗体抗原之间的亲和力为计算标准。抗体按照亲和力的大小进行升序排序。取「μN个抗体作为克隆对象，对第i个粒子进行克隆。

(33)

7) 抗体变异。为了保证粒子的多样性，进行抑制与抗原亲和力抗体变异，并结合抗体间的互斥力关系repk(i,j)，抑制抗体克隆。避免传统粒子滤波的贫化。若repk(i,j)≤Δ，Δ取[0，0.000 1]，设在k时刻第i个抗体进行克隆，并对第j个抗体进行变异。

(34)

式中：randn为(0，1)内的正态分布的随机数；e-repk(i,j)为非线性自适应衰减函数，其引入到变异公式里，是为了提高变异效率，提高粒子多样性，进而加快全局最优搜索。

8) 新抗体群选择。经过抗体克隆与抗体变异得到新的一组抗体，再次进行亲和力计算，并按照亲和力进行排序，并选取N个抗体作为下一时刻的粒子状态集合。人工免疫重采样结束。

3.2 部分人工免疫重采样

为了节省计算量，将对部分粒子进行人工免疫重采样。其具体步骤如下：

(1) 对重要性采样后的粒子进升序排列。

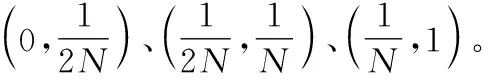
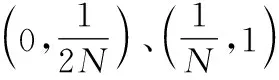
4 算法验证与实验分析

4.1 算法性能仿真实验

为了验证本文提出的基于自适应渐消容积和人工免疫重采样的粒子滤波(AI-AFCPF)的可行性，在非线性与非高斯的系统模型中，采用MATLAB 2018b仿真软件，将本文算法与PF、UPF和CPF进行对比实验，作预测精度和运行效率比较分析。状态模型与观测模型如下：

x(k)=1+0.8cos(0.04πk)+0.6x(k-1)+w(k)

(35)

(36)

式中：w为符合伽玛分布的过程噪声；v为符合高斯分布的观测噪声。

设定粒子数为50个，迭代次数为20次，分别对4种方法进行实验。实验数据表明本文算法在预测精度上明显要高于另外三种算法，四种算法性能比较曲线如图1-图3所示。

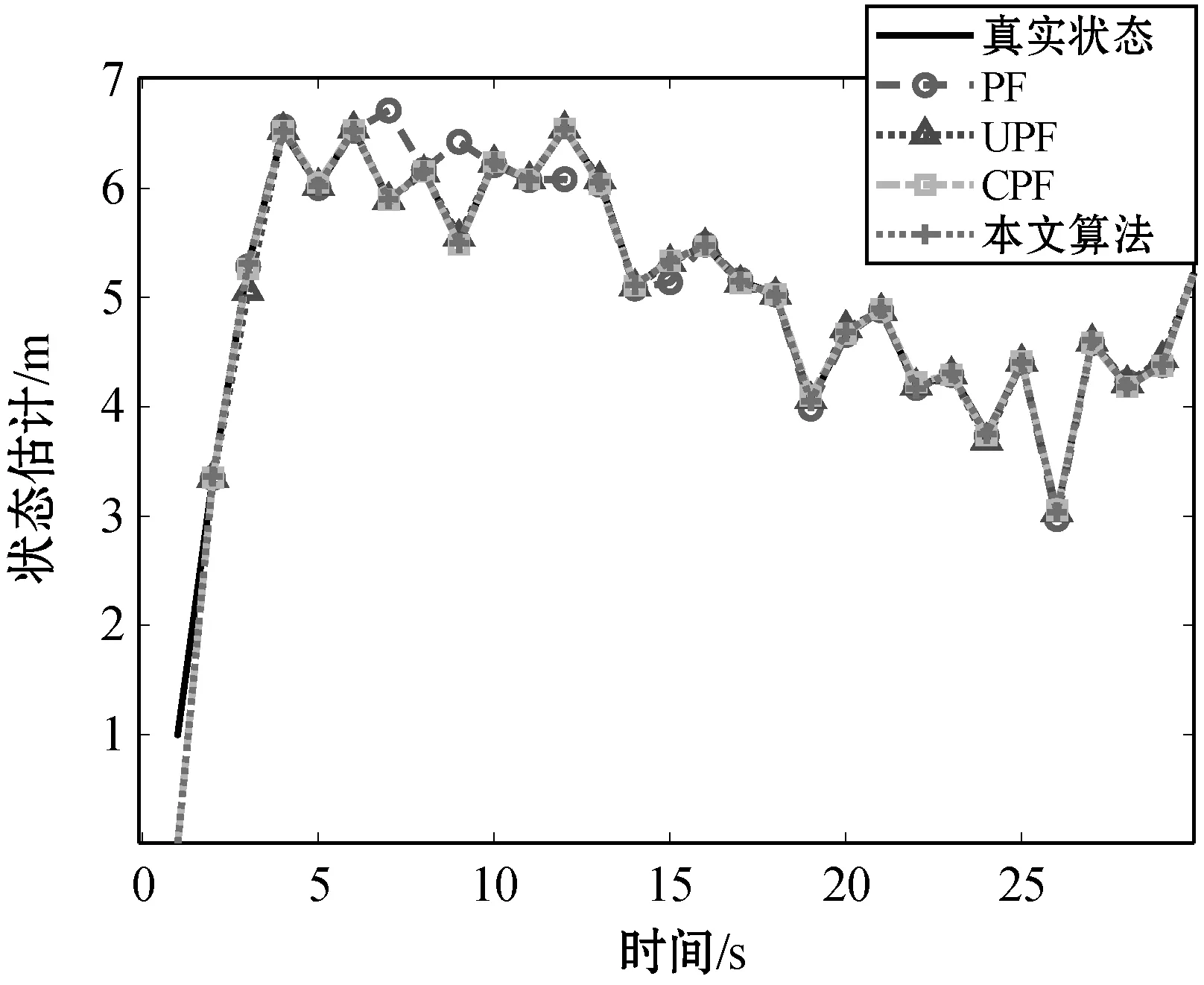
图1 状态估计

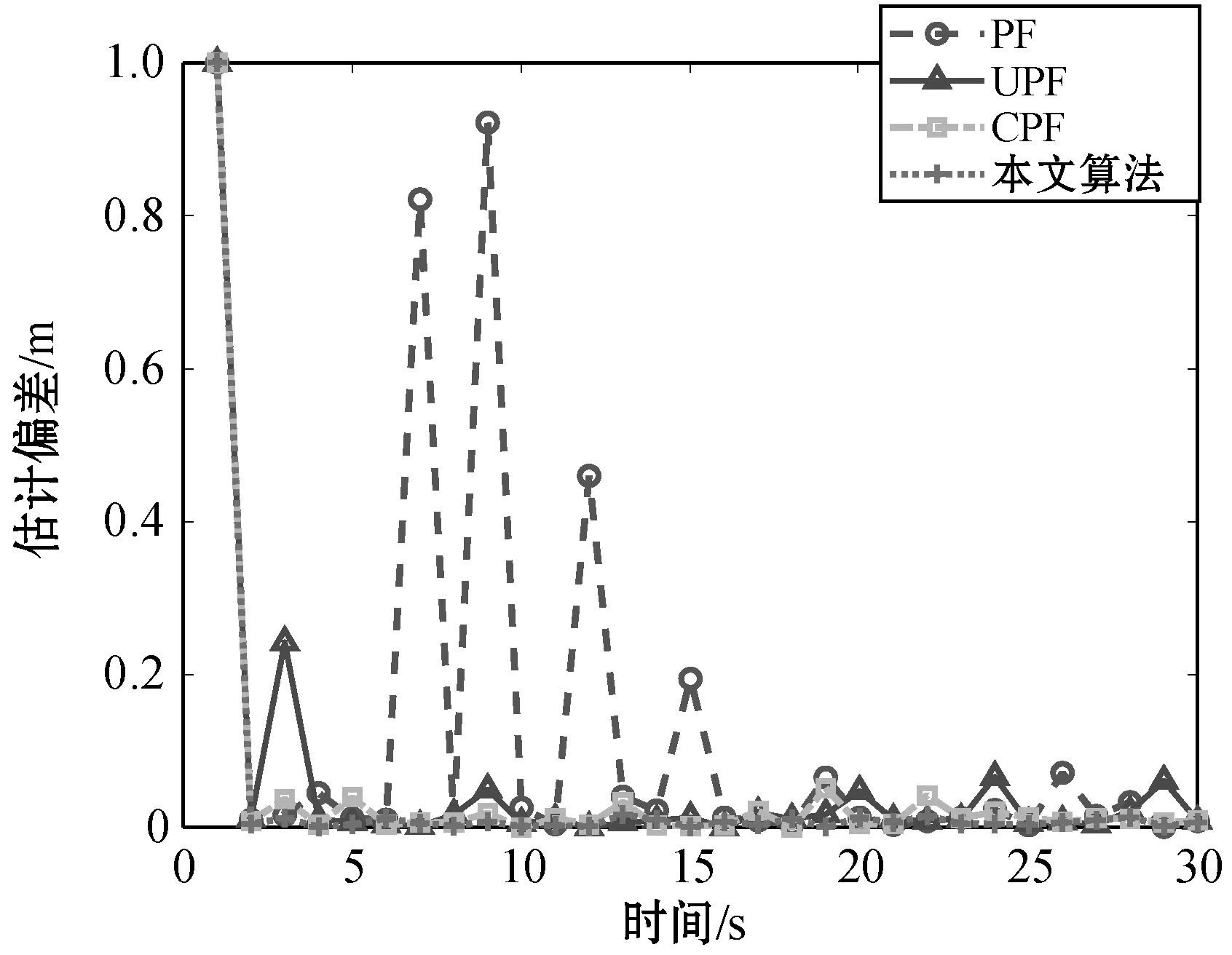
图2 估计偏差

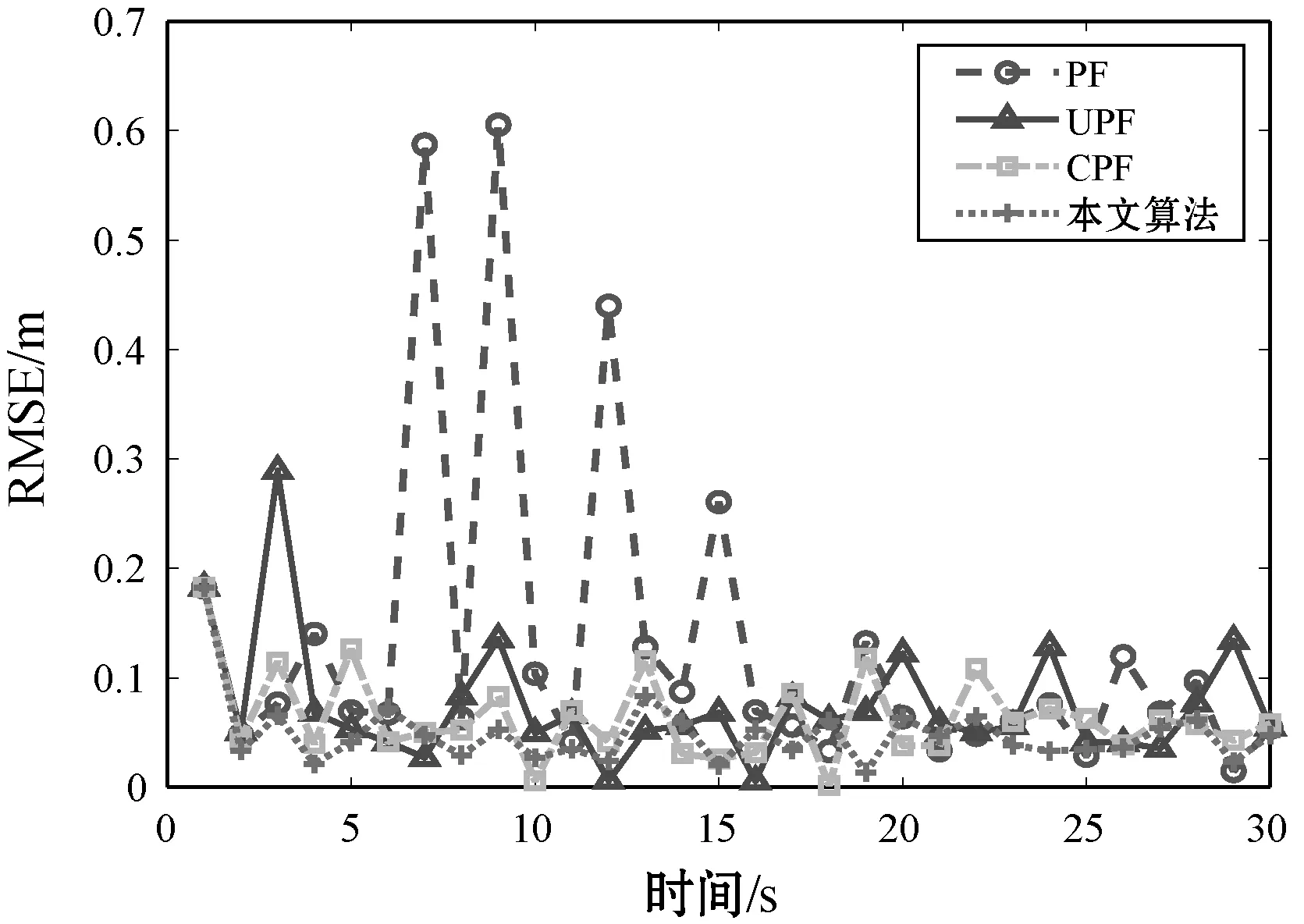
图3 RMSE

为了让算法的性能更加明显，采用均方根误差(RMSE)作为四种算法的状态估计精度衡量标准。四种算法的RMSE的均值和方差如表1所示。根据表1中均方根的均值表明本文算法状态估计误差要低于另外三种算法，均方根的方差表明本文算法在稳定性上要高于另外三种算法，可见本文算法具有更高的预测精度与稳定性。在系统运行上，可以表明本文算法虽然比传统的PF计算量要大，但相比UPF和CPF这两种融合了其他算法的传统粒子滤波要低，所以本文算法具有一定的可行性。

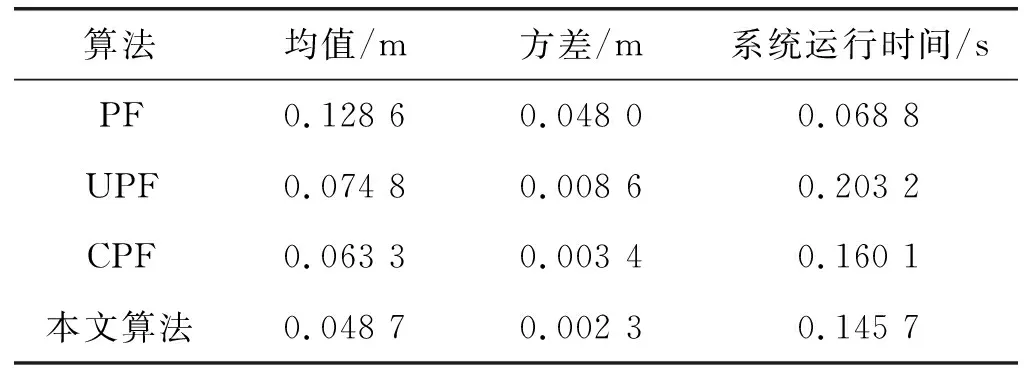
表1 RMSE的均值和方差

4.2 不同粒子数下的算法性能比较

为了分析粒子数对算法的影响，通过在50、70、100粒子情况下进行四种算法的比较实验，并进行10次实验来计算对应算法的RMSE的均值和方差，如图4、图5所示。

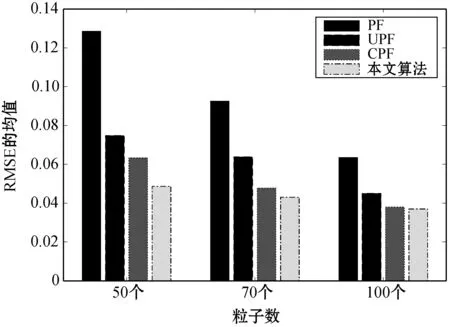
图4 不同粒子RMSE均值对比

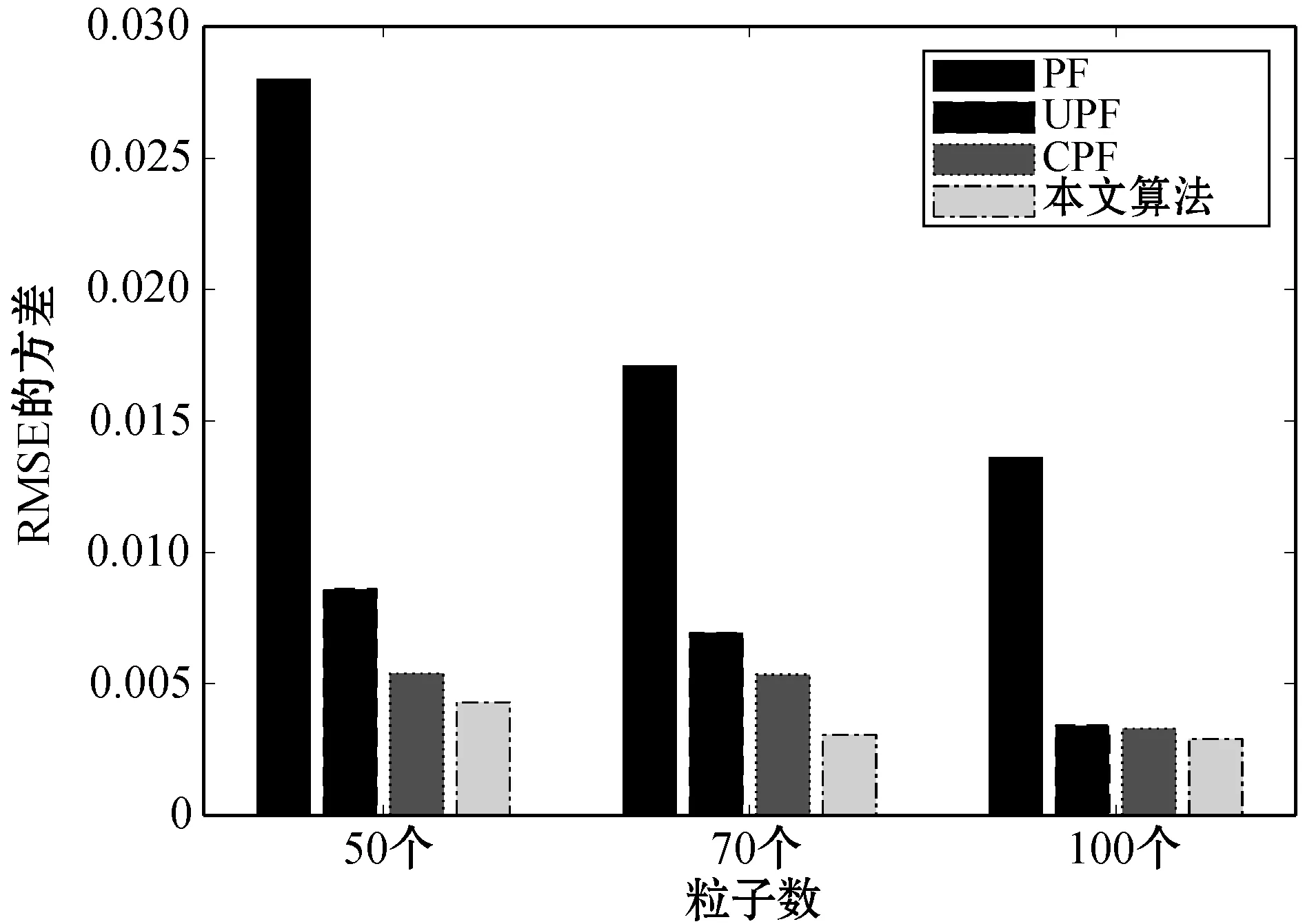
图5 不同粒子RMSE方差对比

从图4、图5分析，没有进行其他算法融合的传统粒子滤波的RMSE均值和方差都远远大于另外三种算法，说明融入其他算法后的粒子滤波提高了稳定性与状态估计精度。另外，随着粒子数不断增加，PF、UPF、CPF三种算法均值和方差也相应下降且下降速率较大，说明这三种算法对粒子的依赖程度较大。而本文算法从柱形图的变化来看相对平稳，可见本文算法对粒子数的依赖性较低，其主要原因是加入人工免疫重采样大大增加了粒子多样性，因此本文算法可以通过较少粒子数达到较多粒子数的性能效果，从而降低计算复杂度，提高系统运行效率。

4.3 目标跟踪有效性实验

为了验证算法的有效性，将本文算法应用于目标跟踪模型上，进行对比仿真实验。实验采用基于距离的目标跟踪模型，因其模型简单、偏差较小、更具实用性，其中观测站为雷达，假设目标做匀速直线运动，在t时刻目标的状态为：

(37)

观测站的状态为固定的点为：

Xstation=(xs,ys)

(38)

考虑目标匀速运动的过程中有干扰噪声所以将目标按水平与垂直方向进行分解，分解如下：

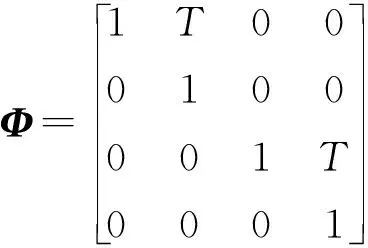
(39)

(40)

式中：T为采样时间点。

观测站与目标状态成非线性关系：

(41)

目标的状态方程和观测方程如下：

X(t+1)=ΦX(t)+Γw(t)

(42)

Z(t)=h(X(t))+v(t)

(43)

设定粒子数为50个，仿真次数为30次，过程噪声Q=diag([0.5,1,0.5,1])，观测噪声设为R=2，进行四种算法目标跟踪得到相应目标运动轨迹和偏差。实验结果如图6、图7所示。

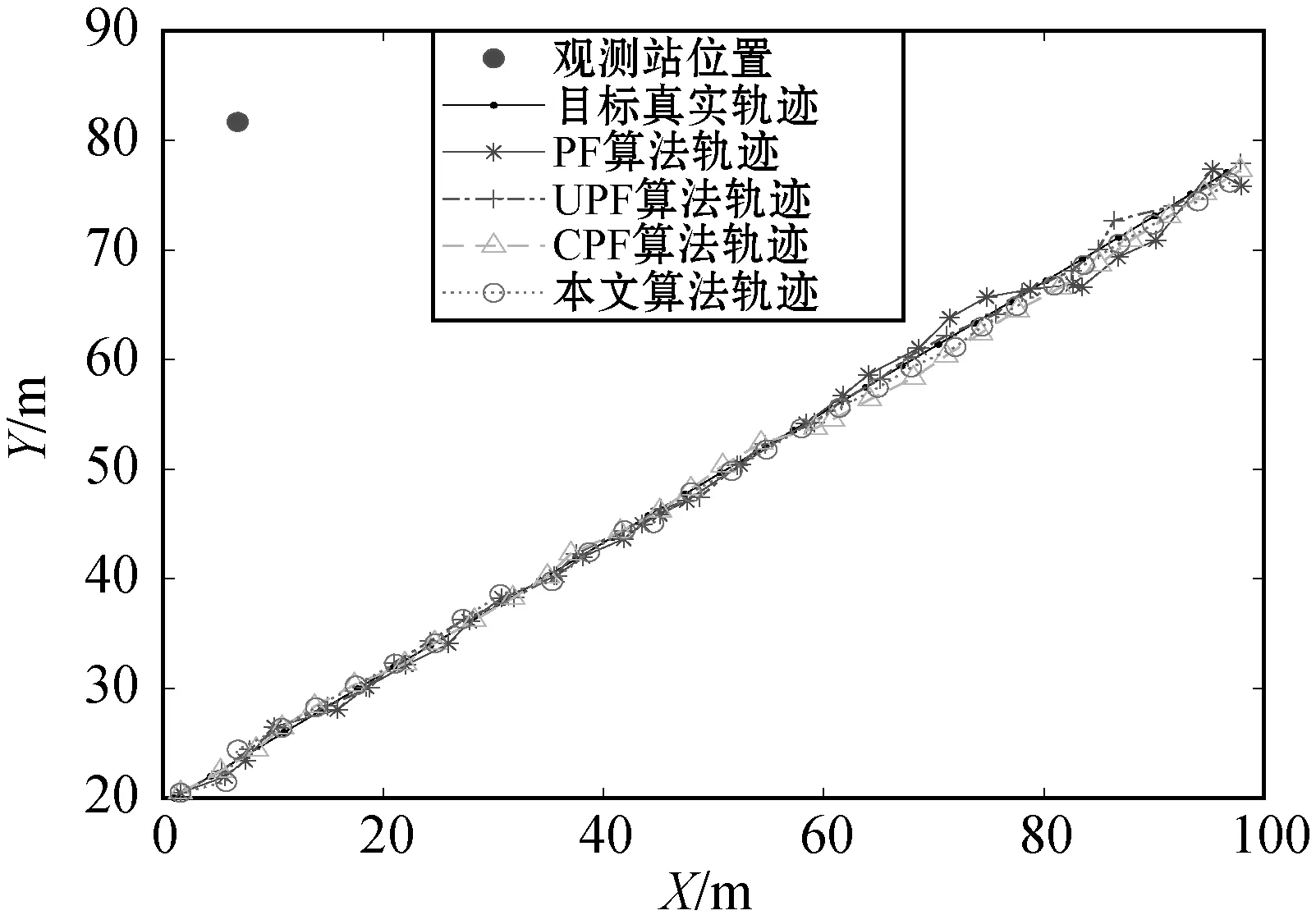
图6 跟踪轨迹

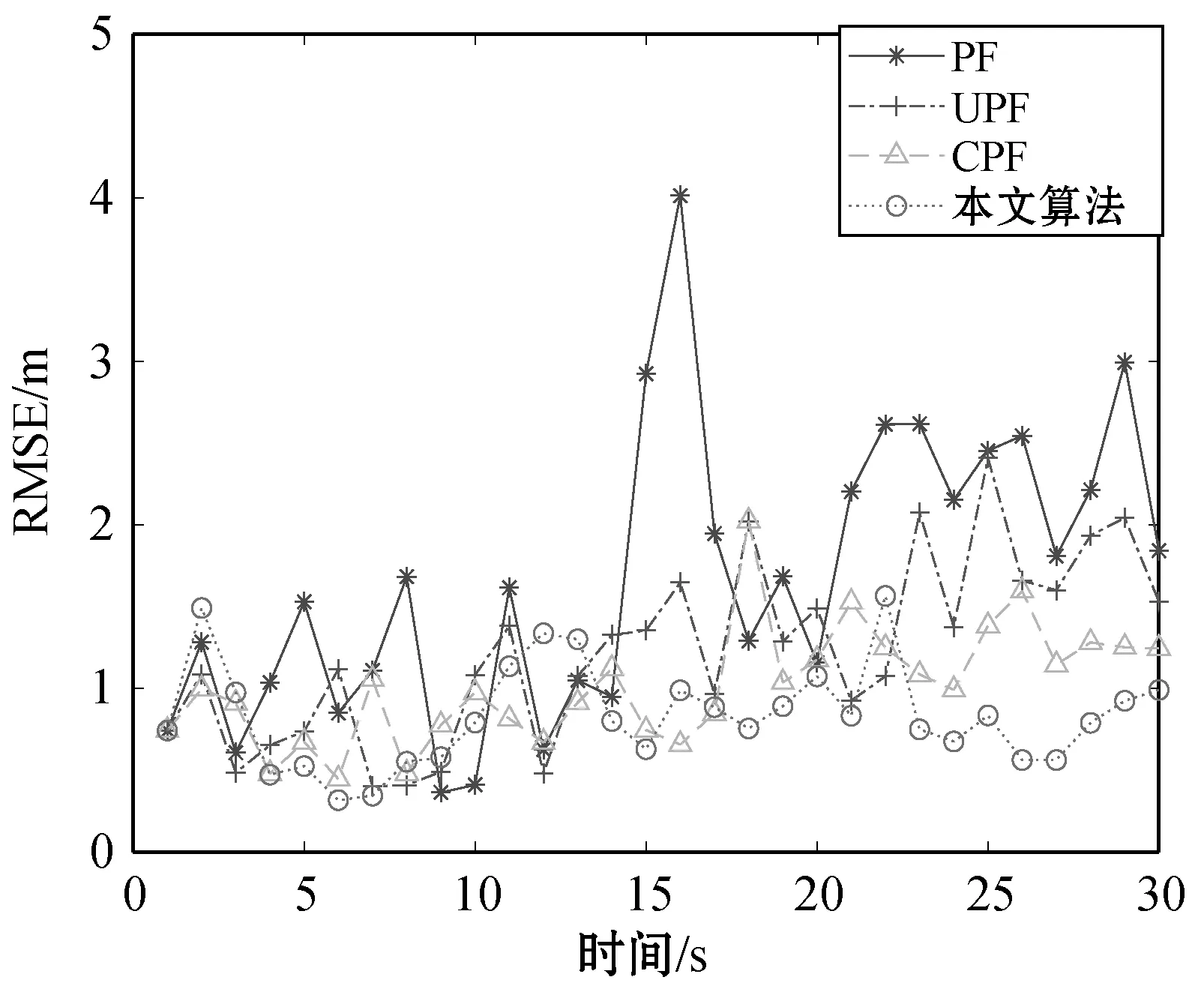
图7 目标跟踪RMSE曲线

从图6、图7分析得基于本文算法的目标跟踪算法相比另外三种算法，估计精度更高，主要是加入自适应渐消容积粒子滤波使得当前观测值加入重要性密度函数这样使得提议分布更加贴近真实分布，渐消因子减少影响状态与观测模型的噪声。根据表2的目标跟踪性能对比，基于本文算法的目标跟踪的RMSE的均值与方差都优于另外三种算法，进一步表明本文算法提高了目标跟踪的精度与稳定性。在系统运行时间上传统粒子滤波虽然运行时间较低，但偏差较大，远远达不到目标跟踪所需误差要求，通常是融合其他算法来弥补误差，计算量相对会增大，但只要运行时间在一定范围内一样具有可行性。基于本文算法的目标跟踪系统在运行整体时间上相比其他两种融合算法少很多，其原因主要是采用了部分自适应人工免疫重采样，保证了粒子的多样性以及算法整体的收敛速度从而降低计算量，很好地满足目标跟踪中毫秒级响应时间的需求，进一步提高系统的估计精度。

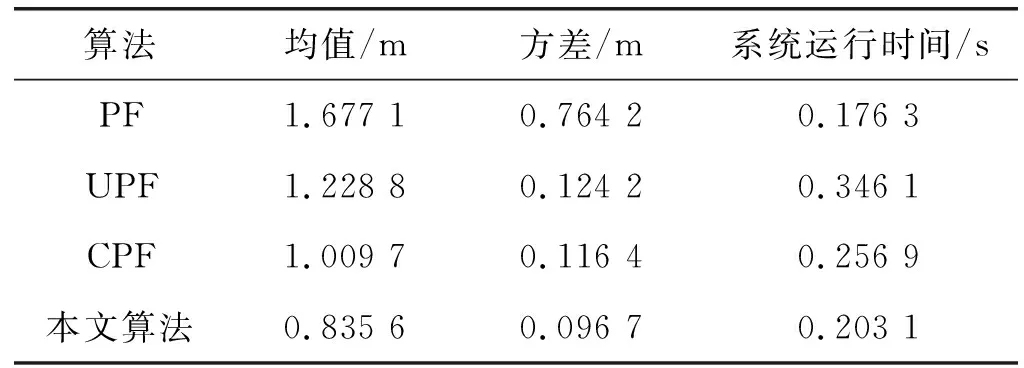
表2 目标跟踪性能对比

5 结 语

本文提出基于自适应渐消容积粒子滤波建议分布，并采用部分自适应人工免疫重采样的目标跟踪方法有效地解决粒子匮乏问题，同时提高了系统的估计精度。此方法主要在容积粒子滤波重要性采样过程融入渐消滤波，其渐消因子对增益矩阵进行在线调节从而使得每个粒子的协方差可以自适应地调节，这样可以有效地使提议分布更加逼近真实的状态分布。在重采样阶段对粒子进行优化组合，对不稳定的粒子集合进行人工免疫重采样，保证系统的稳定性，其中人工免疫重采样利用群智能优化粒子群可以保证粒子多样化，提高估计精度，以及在粒子数较少的情况也能达到较多粒子数的性能从而提高系统运行速率。实验表明本文提出的基于人工免疫的渐消容积粒子滤波目标跟踪算法在估计精度与稳定性都要优于基于PF、UPF、CPF三种目标跟踪算法。因此本文算法在目标跟踪领域具有一定的实用价值。