多策略增强樽海鞘算法下的WSN覆盖优化＊

李 斐，朱晓磊

(1.山东建筑大学信息与电气工程学院，山东 济南 250101；2.山东省智能建筑技术重点实验室；3.积成电子股份有限公司)

0 引言

无线传感器网络WSN 是一种节点密集的分布式网络，其节点是具有一定计算、处理和通信能力的传感器。WSN 通过对信息的传输、处理、存储、显示和控制来实现智能感知，因具有强大的信息探测能力和功耗低、成本低、自组织的特点，在智慧城市、智慧医疗、智慧环保、智慧农业等诸多领域有着广泛应用[1]。

如何部署传感器节点实现对目标区域的网络覆盖范围最大，是构建无线传感器网络的基本优化问题。对于一片二维区域，为保证覆盖范围，经常采用随机抛洒传感器的部署方法，大规模的随机部署可能会产生覆盖盲区或高密度重叠覆盖区，盲区不能满足覆盖要求，而重叠区不仅浪费大量资源，并且过多的冗余数据会产生干扰或堵塞信道。采用确定性部署方式则可以避免以上问题。

近年来，得益于智能优化算法的迅速发展，WSN覆盖优化问题出现了许多良好的解决方案。宋等人[2]提出了基于改进鲸鱼优化算法，采用量子位Bloch 球面坐标编码初始化种群，采用莱维飞行策略跳出局部极值，算法收敛较快，覆盖方案可有效降低节点的冗余。胡等人[3]提出了改进灰狼优化算法，在覆盖优化、覆盖率和收敛速度等方面对于原始灰狼算法均有提升。

樽海鞘算法（salp swarm algorithm，SSA）是一种受深海微生物——樽海鞘的捕食行为启发的优化算法[4]。该算法实现简单，收敛速度较快，在解决单目标的约束优化问题上有较好的鲁棒性和收敛精度，已经成功应用于参数优化、工程调度等问题上。为实现高覆盖率的无线传感器网络的节点部署，本文提出一种多策略增强的樽海鞘算法（ESSA）。使用Halton 序列代替随机序列，生成个体的初始化位置，避免随机点之间有间隙过大和重叠。采用新的非线性收敛因子，平衡算法全局寻优和局部探索能力，加速收敛。引入柯西变异，通过扰动增加个体的多样性，促使个体快速跳出局部最优点。实验表明，ESSA 可以实现WSN快速的高覆盖率的节点部署。

1 多策略改进SSA下的WSN覆盖优化

1.1 樽海鞘算法

樽海鞘是一种类似水母的群居海洋生物，以樽海鞘链的运动形式进行觅食。樽海鞘算法便是模拟它们在海洋中游动和觅食过程提出的优化方法。为了建立樽海鞘群运动觅食的轨迹模型,将种群分为领导者和追随者两类。领导者是在樽海鞘链顶端的个体，朝着食物移动，并且指导着紧随其后的个体。其他樽海鞘为追随者，按照严格的等级制度移动，只受前一个樽海鞘影响。这样的运动模式使樽海鞘链有很强的全局探索和局部开发能力。

建立优化算法的数学模型。假设可行域内种群规模为N，解空间的维度为D，领导者的位置更新表示为：

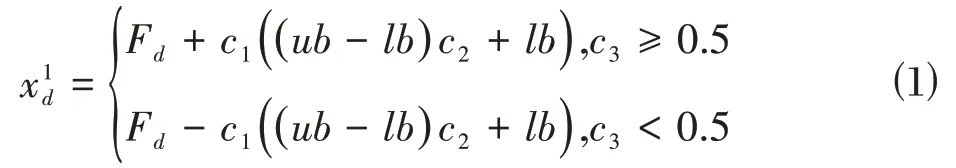
其中，l是当前迭代次数，L是迭代次数上限。由式⑵可知收敛因子是一个从2 到0 的递减函数。其他追随者的更新公式如下：

1.2 Halton序列初始化

种群初始化的位置影响种群的多样性，随机初始化位置往往是分布不均匀的伪随机序列，导致初始的传感器节点之间有间隙过大和重叠的可能。虽然迭代初期最优解未知，但若搜索的起始位置更加均匀的分布在整个解空间，则会加快寻优的进程，为此，本文采用Halton序列初始化樽海鞘群体的位置。Halton序列是一种随机序列[5]，被用来生成均匀分布的随机数，原理是选取一个质数作为基数，然后在[0,1]内不断地切分，从而形成一些不重复并且均匀的点，本文采用Halton 序列生成传感器节点的初始坐标，需乘以区域边长以将其拉伸到可行域中。

1.3 新的非线性收敛因子

原始SSA 算法的非线性收敛因子如公式⑶所示，为了进一步提供算法收敛性，本文提出一种新的非线性收敛因子，如公式⑷。

对比二者的变换曲线，如图1所示。

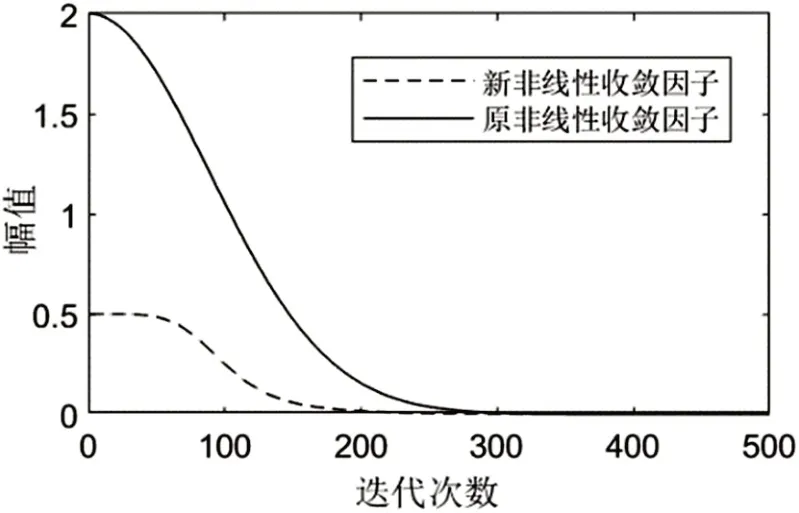
图1 新旧非线性收敛因子幅值对比

由图1可知，新的收敛因子取值范围更窄，向横轴靠拢的速度更快，这会加快前期算法的收敛速度，迭代后期两条曲线几乎重合，此时算法的收敛性相当。新非线性收敛因子的对性能的提升见实验3.1。

1.4 柯西变异

按照一定概率对个体的某位置进行变异，从而产生新个体，可有效增加种群的多样性，避免迭代陷入局部极值，因此在SSA 迭代中引入个体的柯西变异机制。标准柯西分布比标准高斯分布更加矮宽，具有更大的拖尾[6]，领导者按照柯西分布随机产生较大扰动，变异公式如公式⑸。

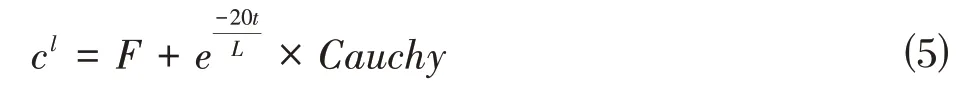
其中，cl是第l次迭代产生的柯西变异个体，F为当前最优解，Cauchy表示与个体位置向量维度相同的标准柯西分布产生的点。在本文中，优化对象是二维空间中的坐标，因此，每个个体的维度是2，Cauchy可以由以下公式获得：

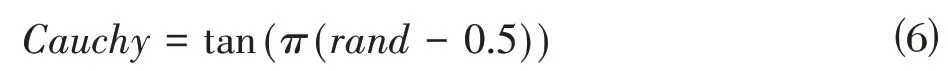
其中，rand是一个1× 2大小的[0,1]上的随机数。

比较变异个体与当前最优解的适应度函数值，更新最优解。

1.5 算法流程

本文采用布尔感知模型[7]，即传感器节点对位于距离R 范围内检测区域节点的感知能力相同，因而传感器节点的感知范围是以传感器节点为圆心、以R 为半径的圆盘。若给定传感器数目，节点部署的目标函数为给定区域内的覆盖面积之和，优化各个传感器的坐标，使覆盖面积尽可能地大。ESSA 算法下的WSN覆盖优化流程如图2所示。

图2 ESSA算法下的WSN覆盖优化流程图

2 实验结果

2.1 改进策略的有效性

针对WSN 网络节点部署的覆盖问题，首先考查SSA的改进策略的有效性，进行消融实验，即分别考查三种改进策略单独使用时的迭代曲线。设目标区域的大小为100×100，传感器节点数为40，每个节点的通信半径为10。优化算法的种群大小为20，最大迭代次数为500。SSA 算法在各个改进策略下的迭代曲线如图3所示。

图3 SSA在不同改进策略下的迭代曲线对比

观察图3 可见，三种改进方式均可以提升原始SSA 算法的收敛性或精度。其中，新的非线性收敛因子可以明显提高迭代中前期的收敛性和精度；Halton序列初始化会在迭代前期表现出非常明显的精度优势，但却趋于平坦，陷入局部极值的时间较长；Cauchy变异虽在迭代最初曲线较低，但胜在收敛性好，几次迭代后曲线快速提高，并且迭代结束后达到最高的精度。表现最好的为本文提出的多策略ESSA，可以将三种改进策略优势互补，获得起点高、收敛快、精度高的特点。

2.2 WSN覆盖优化

考查ESSA 在WSN 覆盖优化问题上的性能，采用SSA、灰狼算法（gray wolf optimization algorithm,GWO）、鲸鱼算法（whale optimization algorithm,WOA）群智能方法进行对比。实验设置同3.1 节。覆盖率关于迭代次数的分布曲线如图4所示。

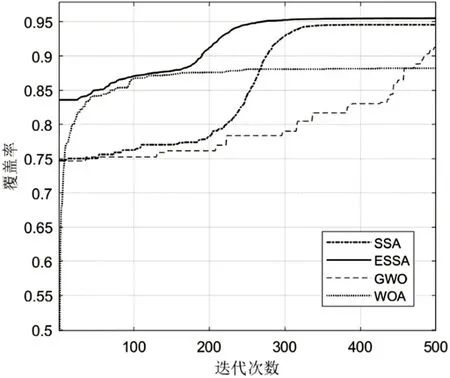
图4 四种群智能方法的迭代曲线对比图

从迭代曲线可以看出GWO 算法的收敛性差，因此迭代结束时精度不高，覆盖率仅为91.33%；WOA 迭代初始起点低，但是收敛速度快，然而算法陷入局部极值无法跳出，产生早熟，在100次迭代后曲线趋于平坦，导致最终覆盖率最低，为87.66%。ESSA 收敛迅速，精度高，最终取得最高的覆盖率95.64%。

考查ESSA 的节点部署结果，采用随机抛洒和SSA、GWO、WOA 群智能方法进行对比，部署结果如图5所示。

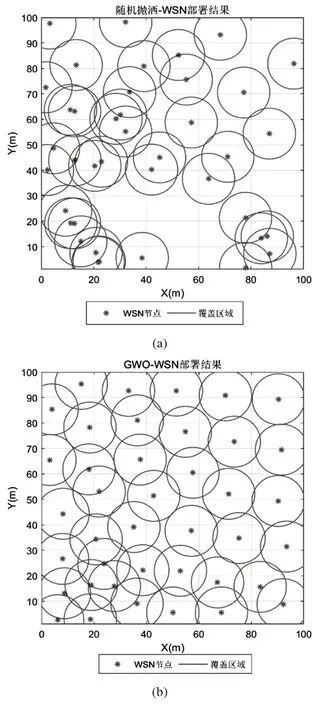
图5 五种算法的WSN的节点部署结果

图5 中每个星号表示传感器的部署位置，以此为圆心的圆圈表示该传感器的感知范围，全部圆圈的覆盖面积之并集即为总覆盖面积，覆盖率为总覆盖面积除以方形区域面积。部署结果与迭代曲线所反映的趋势一致。随机抛洒部署方法的空白区最多，重叠也最为严重，为了保证覆盖率，需要更多的传感器，这带来资源浪费和信号干扰问题。其他优化方法也有一定的覆盖重叠区域，导致覆盖率降低。ESSA 方法的节点分布最为均匀，覆盖面积最大，这一优势是由改进策略带来的。

3 结束语

本文提出一种多策略增强的樽海鞘优化算法，进行无线传感器网络的节点覆盖优化。在Halton序列初始化、新非线性收敛因子及柯西变异策略下，优化算法的性能得以提高。与其他群智能方法的对比实验看出，ESSA 是一种优化过程起点高、收敛迅速、精度高、覆盖率高的WSN节点部署方法。