基于ESPI技术的混凝土单轴拉伸断裂特性研究

龙津润，赵炳震，陈红鸟，许应杰

(1.贵州大学空间结构研究中心，贵阳 550025；2.贵州大学，贵州省结构工程重点实验室，贵阳 550025； 3.陕西建工未来城市创新科技有限公司，西安 710086)

0 引 言

混凝土作为一种用途最广、用量最大的建筑材料，为了充分发挥它的优势，应全面研究其各项性能。纵观混凝土的研究史，对于其抗拉性能的研究远远少于其他性能，但随着高拱坝等薄壳结构建筑物的出现，混凝土的拉伸性能被逐渐重视。拉伸性能对混凝土结构的安全起着重要的作用，不少建筑在长年累月的使用中在各种荷载作用下，由抗拉强度或拉伸变形不足而导致开裂，进而引起结构的破坏，造成安全隐患。断裂特性直接关系到结构安全性与耐久性，对于它的研究也是不可或缺的。因此，研究混凝土单轴拉伸的断裂特性具有重要意义。

为研究混凝土的断裂特性，对混凝土断裂过程区变形的测量与讨论十分关键。关于断裂过程区，徐世烺等[1-3]已做过大量研究，提出了相关的断裂准则；唐宇翔[4]对混凝土和石墨的断裂过程区也进行了很多研究，利用逐点位移法做了拉伸软化曲线相关研究，并总结了断裂特性；针对Ⅰ、Ⅱ型断裂过程区的数值模拟也已有学者[5]进行了研究。在混凝土断裂过程中，能量的释放与裂缝的扩展存在关联，因此有研究者[6]对断裂中产生的能量进行了讨论。对于断裂性能的研究，王德强[7]对三点弯曲梁在往复荷载作用下进行了一系列试验，得到相关断裂性能的特点。

关于混凝土的拉伸性能，很多学者[8-13]对其做过很多传统的研究，包括力学性能研究、本构关系研究以及相应的数值模拟等。基于传统的研究结果，不少学者将相关研究方法延伸更广。何吉等[14]研究了全级配混凝土抗拉性能的随机性，并做了相关的数值研究；田梦云等[15]在细观层面对混凝土的单轴拉伸进行了计算机仿真试验，得到的仿真结果与真实结果十分接近。不少学者也将上述研究技术应用于更广泛的材料中，纪恩武[16]研究了超高韧性水泥基复合材料(UHTCC)在单轴往复荷载下的动力性能；赵一鹤等[17]采用超高性能混凝土(UHPC)材料研究了不同钢纤维含量对拉伸性能以及拔出性能的影响。

裂纹的扩展是动态的，但是传统的测量方法难以捕捉动态关系，无法研究混凝土内部骨料间的相互作用以及裂纹扩展原理，很难对断裂特性进行研究，因此需要引入新的技术。电子散斑干涉(electronic speckle pattern interferometry, ESPI)技术测量精度高，测量范围广，且适用于变化梯度较大的局部变形测量，如裂缝尖端位置处的变形等。因此，ESPI技术是探究混凝土断裂特性的一种高效实用的测量技术，在传统方法的基础上进一步加深了对混凝土的研究。徐世烺等[18]以电测法为辅助，使用激光散斑照射法对带有预制切口的混凝土梁进行观测，得到试件梁中微裂缝亚临界扩展的应力场分布及其变形规律。孙平等[19]把ESPI技术应用到了三维研究中，开创了一条新的研究道路。潘建伍等[20]基于ESPI技术对纤维混凝土加固进行了研究。王青原等[21]基于ESPI技术对混凝土裂纹扩展特性进行了研究，探究了裂纹扩展规律，得到了判断断裂过程区的方法。目前采用ESPI技术对混凝土三点弯曲裂纹扩展规律以及断裂特性的研究较多，但是对混凝土单轴拉伸断裂特性的研究相对较少。

本文利用ESPI技术对混凝土棱柱体单轴拉伸试验中试件表面的场位移进行测量，计算混凝土的相关断裂参数，分析混凝土断裂过程中的特点以及裂纹的扩展规律。

1 ESPI技术原理图

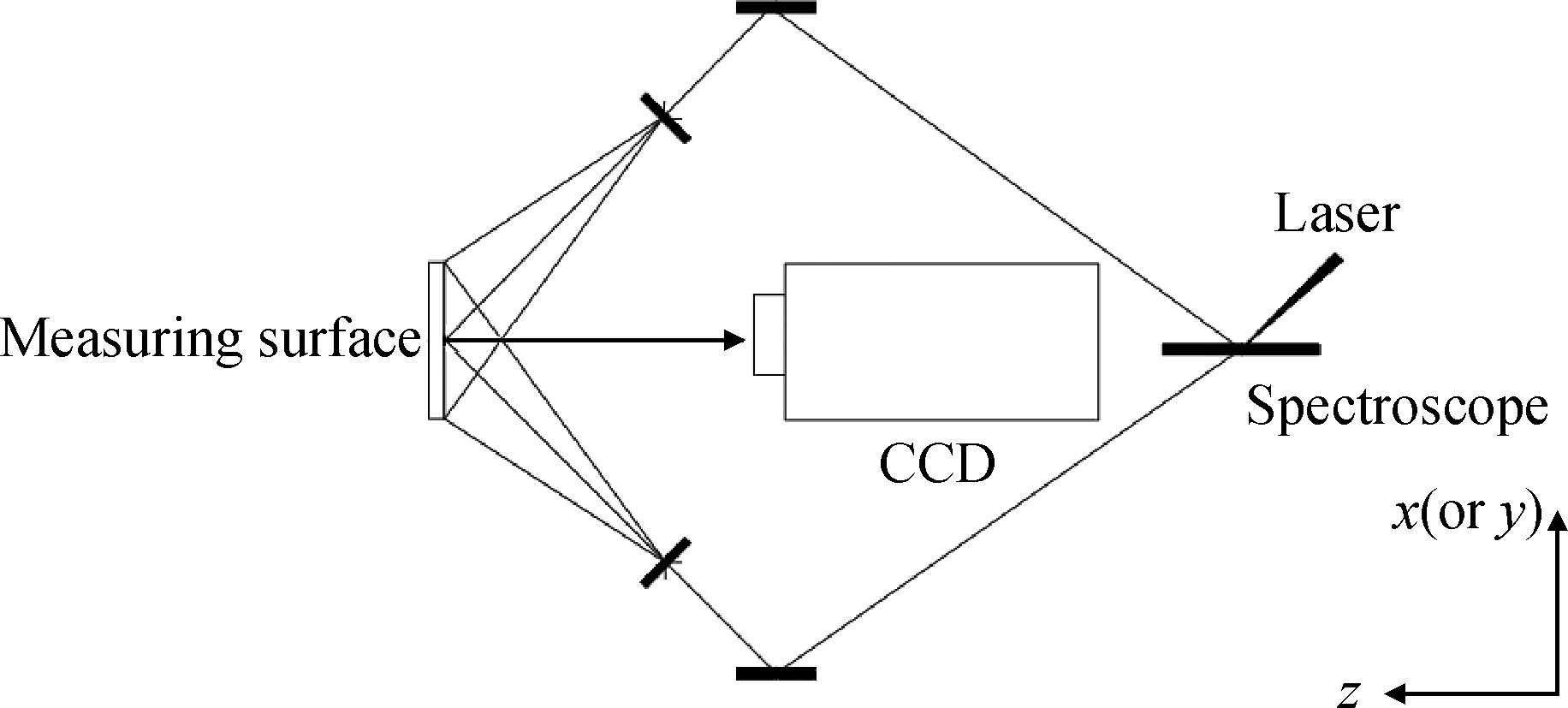
图1 ESPI技术测量原理图Fig.1 ESPI technology measuring schematic diagram

ESPI技术使用散斑作为被测量物体位移场变化的载体，以被测物体位移场变化前后的参考光和物光作为研究对象，借助电荷耦合器件(charge coupled device， CCD)相机完成对两者间干涉图像的测量。对变形前后所得到的数字图像进行减法处理，从而得到相应的条纹场。条纹场与强度间存在着关联性，因此可借助干涉条纹来实现对整个场变形大小以及分布的测量。

ESPI技术测量原理图如图1所示。激光首先被分光镜分为物光和参考光，两束激光上下对称照射于待测物体粗糙表面，随后两部分光通过反射并在CCD相机上发生干涉形成散斑图，最后通过将变形前后的散斑图相减得到位移云图。

取测量表面上的任意一点，设参考状态下两束光变形之前的相位为φ，变形之后的相位为φ′，且φ′=φ+Δ。图2为相位变化示意图。在此状态下通过CCD相机拍摄出干涉光斑图，每张干涉光斑图的强度(Im)计算如式(1)所示。

(1)

式中:IA和IB分别为物光和参考光的强度；φ为两干涉光的干涉相位；Δ为相位差。

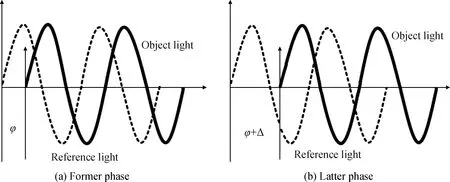
图2 相位变化示意图Fig.2 Schematic diagram of phase change

平面内位移u可以由式(2)计算得到。

(2)

平面外位移d可以由式(3)计算得到。

(3)

式中:λ为激光波长；α为照射光的入射角。

最后，通过ESPI技术专用数据分析软件ISTRA得到被测表面的应变和位移信息。

2 实 验

2.1 试件制备

试验采用C80高强混凝土，其配合比如表1所示。水泥型号为Portland CEM I 52.5 N，细骨料为细砂，粗骨料为花岗岩,骨料的最大粒径为10 mm，级配为单粒级配。共浇筑了立方体、圆柱体和棱柱体三种类型试件。其中立方体试件尺寸为150 mm×150 mm×150 mm，用于测量立方体抗压强度；圆柱体试件尺寸为φ150 mm×300 mm，用于测量弹性模量；带有预制切口的棱柱体试件尺寸为250 mm×60 mm×50 mm，预制切口深度为5 mm，宽度为2 mm，用于单轴拉伸试验。浇筑完成后，试件在自然环境(温度为(20±2) ℃，相对湿度为75%～85%)下养护28 d。

表1 混凝土配合比Table 1 Mix proportion of concrete

2.2 试验装置

采用MTS试验机对混凝土棱柱体试件进行单轴拉伸试验，试验装置示意图如图3所示。在试验中，底部支座向下移动施加竖向荷载，顶部支座固定。为了保证轴向拉伸时荷载不发生偏心，在试件两端预埋钢管，并通过定制的转动轴承将混凝土试件与MTS试验机连接在一起，以保证轴向拉伸试验的实施。

轴向拉伸试验的加载方式采用位移加载，加载速率为0.001 mm/min。通过在试件左右预制切口端部放置两个夹式位移计，得到试件梁的预制切口端部裂缝口张开位移(crack mouth opening displacement, CMOD)。采用线性位移计来测量试件伸长量。在预埋钢管端部混凝土表面粘贴应变片，测量附近位置应变分布,通过数据采集仪记录整个过程的荷载-位移曲线。

将CCD相机固定于支架上，调整CCD相机镜头以确保能够对试件表面的中心区域进行观察。为测量棱柱体表面的位移场，试验采用ESPI技术装置配备Q300系统，Q300系统的位移测量精确度为0.05～1.00 μm，能够满足试验精度的要求；CCD相机的像素分辨率为1 392×1 040，能够清晰记录试件破坏情况。综上所述，ESPI技术能完全满足此次试验的精度需求。试验过程记录照片如图4所示。

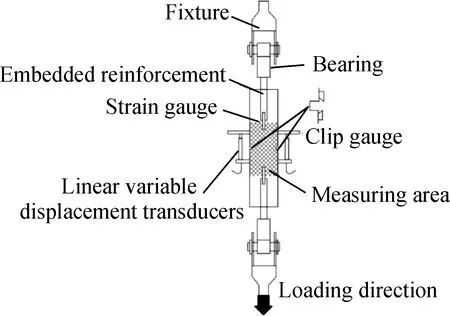
图3 单轴拉伸试验装置示意图Fig.3 Device schematic diagram of uniaxial tensile test

图4 试验过程记录照片Fig.4 Image of experiment process

2.3 试验计算方法

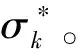
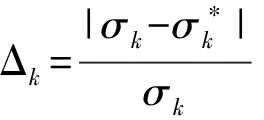
(4)

式中：Δk为试验值与计算值偏差。假定接受阈值Δcri，本文中取3%。当Δk<Δcri，Δk+1>Δcri时，可认为(εk，σk)为初裂点。

(2)系数陡降法[22]：代入应力-应变曲线数据点(εi，σi)，计算系数r。系数r的数值在陡降时对应于应力-应变曲线上的点即为初裂点，r计算公式如式(5)所示。

(5)

3 结果与讨论

3.1 荷载-位移曲线

本试验通过对四个棱柱体试件进行直接拉伸，通过读取压力机的荷载值P以及左右线性位移计测量值的平均值δ得到四条荷载-位移曲线，结果如图5所示。各试件在加载初期荷载-位移均能呈一定的线性关系，随着荷载增加到约8 kN时，曲线斜率逐渐降低，表明试件从线弹性阶段进入非线性阶段。此阶段下由于裂缝的扩展，骨料之间相互作用力降低，混凝土内部结构损伤程度逐渐增加，刚度退化，从而使曲线斜率不断减小。各个试件的曲线变化较为相似，峰值荷载具有一定离散性，峰值荷载对应的位移大小接近，约为0.018 mm，当荷载达到11 kN左右时试件发生断裂，其数值上下波动约10%。整条曲线展示了混凝土在拉伸过程中从线弹性阶段进入塑性损伤阶段最后发生断裂的全过程，也对应着裂缝的起裂、稳定扩展和失稳扩展三个阶段。

3.2 荷载-裂缝口张开位移曲线

分析Test 1，记录ESPI与夹式位移计测量得到的左端裂缝口张开位移(CMODL)与右端裂缝口张开位移(CMODR)，计算得到平均CMOD，将两种方式下P-CMOD曲线进行对比，图6为P-CMOD对比曲线。

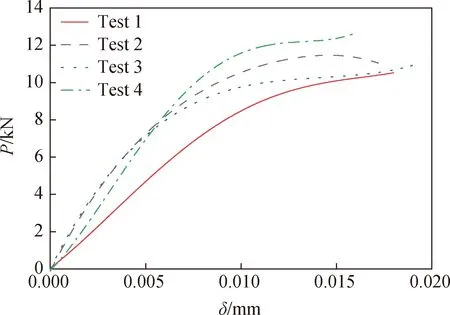
图5 试验荷载-位移曲线Fig.5 Load-displacement curves of tests

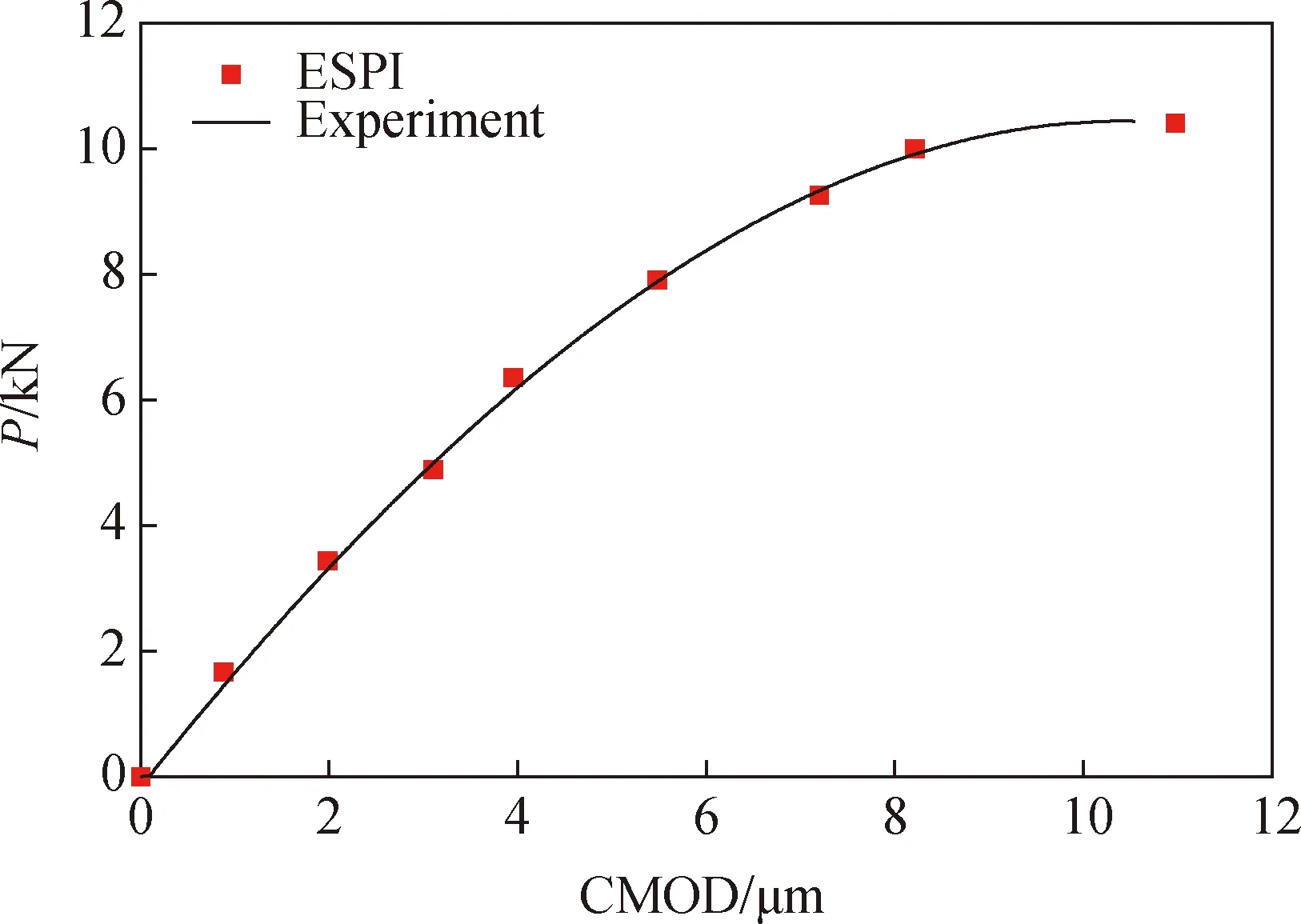
图6 ESPI与试验中P-CMOD对比曲线Fig.6 Comparison of P-CMOD curve between ESPI and experiment

分析图6可知，夹式位移计结果与ESPI测量结果在整个阶段都比较吻合，CMOD最终达到11 μm。在加载初期有一些偏差，产生偏差的原因有两个方面：(1)随着裂缝的扩展，试件在受拉侧产生竖直方向的刚体位移；(2)在加载前期，CMOD数量级较小，而且夹式位移计精度小于ESPI，数值也是由小到大，导致初期偏差跟后期相比更大。综上，在加载过程中两者测量会出现一些偏差，均在5%以内，测量精度仍能满足研究需要。整体来看，ESPI结果与夹式位移计结果吻合较好，证实了ESPI技术在本研究中的可靠性与精确度。

3.3 断裂参数计算

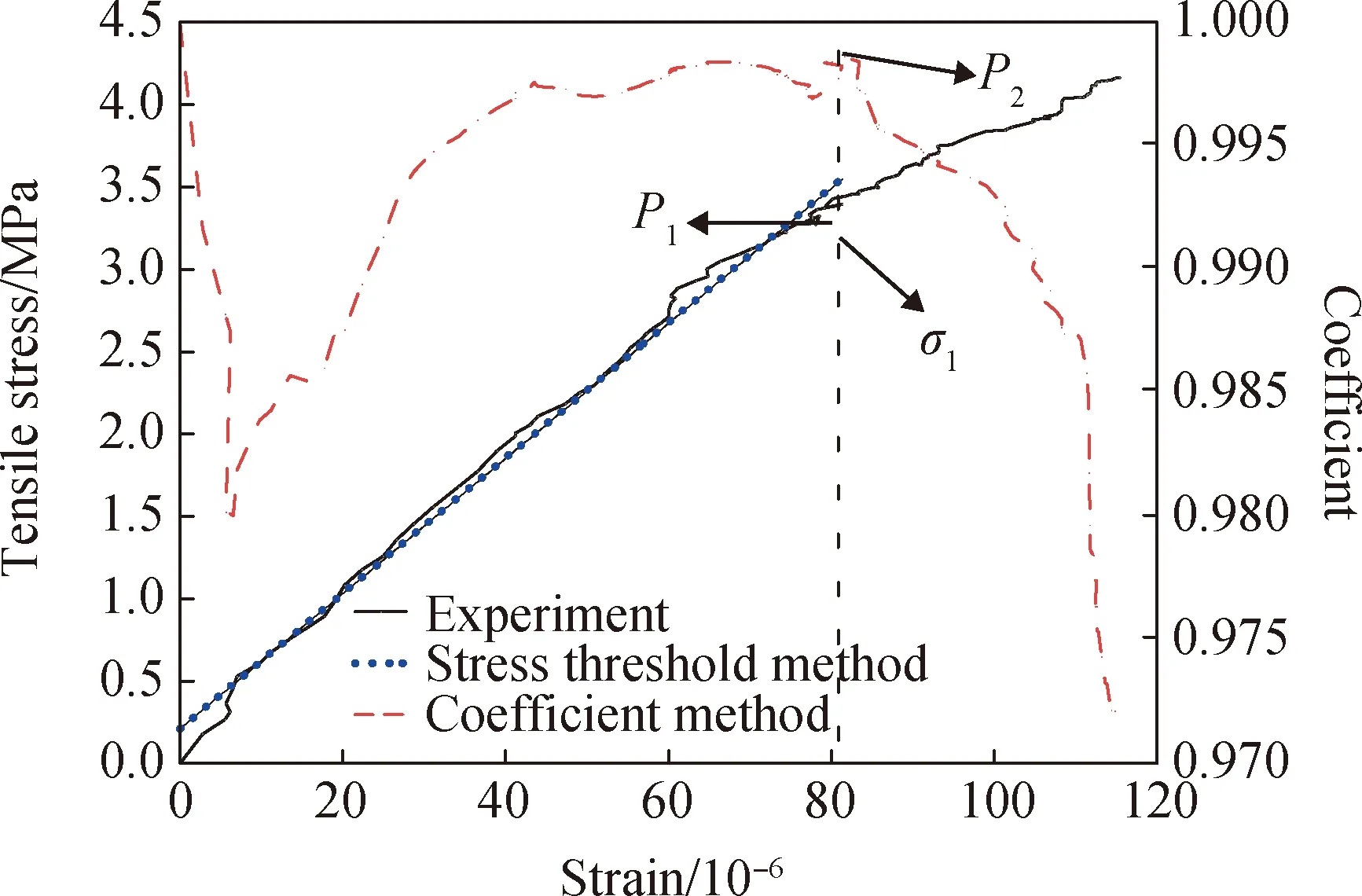
图7 初裂点判断示意图Fig.7 Schematic diagram for judgement of initial crack point

(1)初裂点拉应力(σ1)：将测量得到的荷载-位移曲线转化为应力-应变曲线，其中应力σ=P/A1(A1为韧带面积，其大小等于棱柱体横截面面积A减去预制切口面积，本试验中A=3 000 mm2，A1=2 500 mm2)，应变ε=δ/L(L为测量标距，本试验中为150 mm)，再利用上文所提及的线性阈值法和系数陡降法[22]计算。利用线性阈值法计算得到的终点P1以及系数陡降法得到的陡降点P2(如图7所示)对应的横坐标为应变投射在试验曲线上的点即为初裂点(也称不连续点)，初裂点强度作为反应混凝土材料强度储备大小的物理量，具有重要的工程价值。

由图7可知，两种方法得到的初裂点结果基本相同，认为该点即为初裂点。可以得到初裂点应力为3.44 MPa，约为峰值应力的82%，对应的微应变为81，约为极限拉应变的66%。

(2)弹性模量(E)：根据文献[23]并结合应力强度因子手册[24]，对带有两个预制切口的混凝土试件进行单轴拉伸时，可以得出P-CMOD的关系，如式(6)、(7)所示。

(6)

(7)

式中：V1表示CMOD的几何因子；a为预制切口长度；b为试件宽度；σm=P/A。取同一试件在加载初期(线弹性变形阶段)三个时间点对应的(σm，CMOD)，即可计算出弹性模量，结果见表2。

表2 弹性模量计算参数Table 2 Calculation parameters of elastic modulus

由上述方法计算得到的弹性模量为34.53 GPa,与圆柱体试件测得的弹性模量34.06 GPa相近，误差不到2%。

(3)断裂韧度(KIc)：根据应力强度因子手册[24]，利用式(8)、(9)可以计算得到应力强度因子K1。

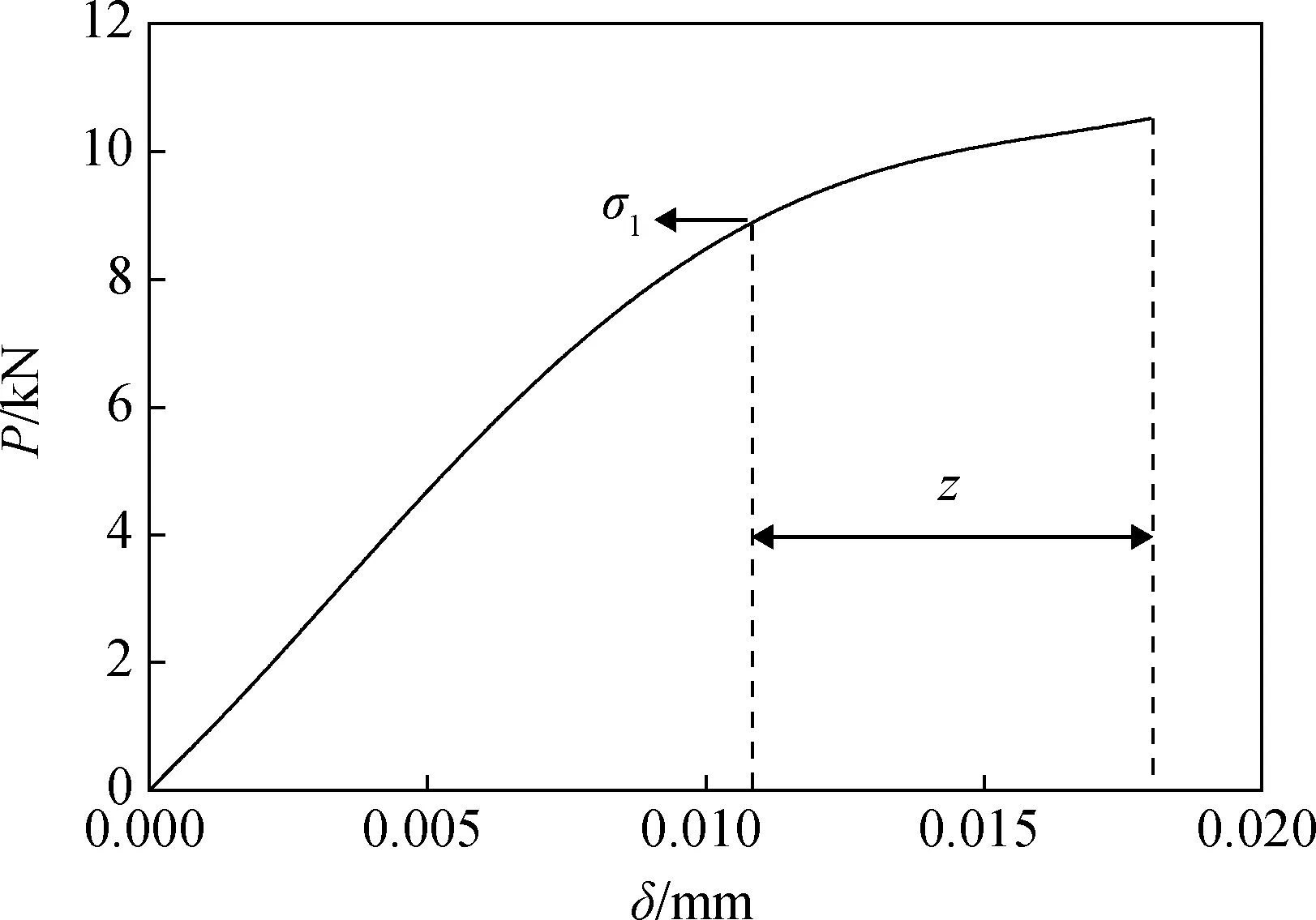
图8 z计算示意图Fig.8 z calculation schematic diagram

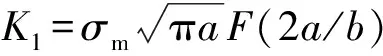
(8)

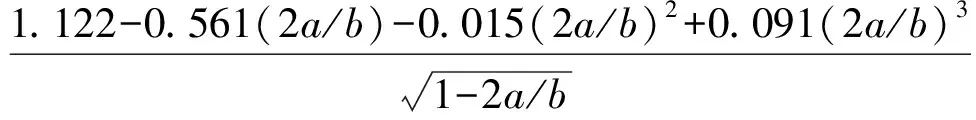
(9)

F表示K1的几何因子，将上文所计算得到的初裂点应力σ1换算为相应的σm，σm=0.83σ1，代入式(8)、(9)即可求得起裂韧度，即断裂韧度。

(4)上升段断裂能(GFS):根据文献[22]中的断裂能计算公式

(10)

式中：z表示裂缝宽度，z计算示意图如图8所示。

将上述计算结果进行汇总，如表3所示。

表3 断裂韧度计算参数Table 3 Calculation parameters of fracture toughness

3.4 曲线拟合

基于试验所得的峰值应力以及对应的峰值应变，根据吴锋[22]提出的修改后的Reinhardt拟合公式[25]，可以得到拟合曲线，拟合公式如式(11)所示。

(11)

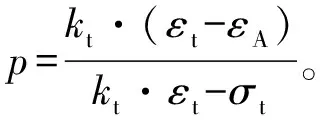
非线性阶段也可利用变化后的高斯拟合公式进行曲线拟合预测，建立的计算公式如式(12)所示。

σ=σte-c(εt-ε)d

(12)

式中：c、d为参数，分别控制了上升段非线性的斜率以及平缓部分的初始位置与高度。式(12)中的参数可由最小二乘法获得，具体做法如式(13)所示。

(13)

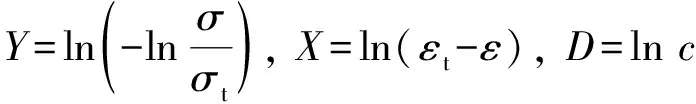
(14)

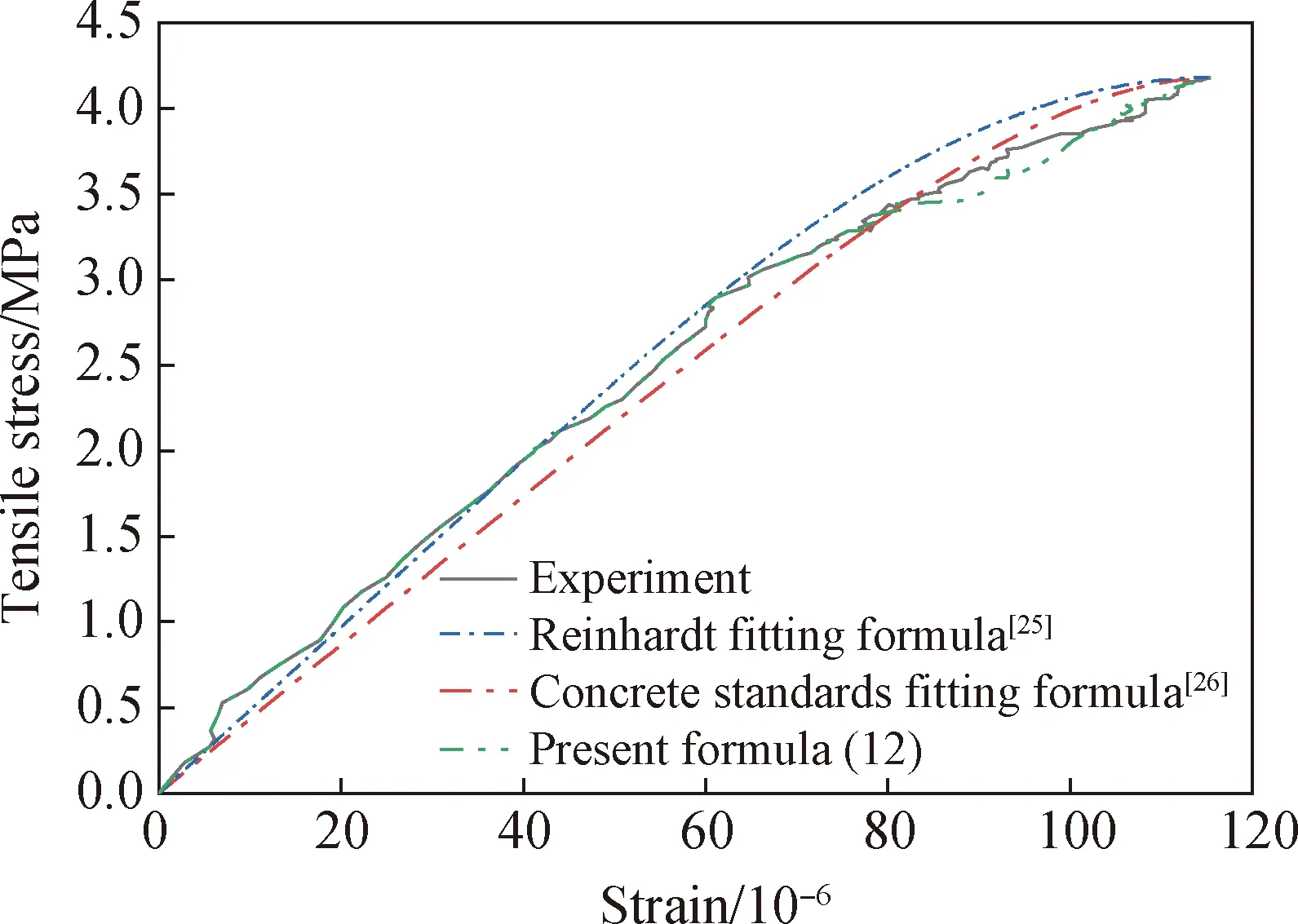
图9 应力-应变的拟合曲线与试验曲线对比Fig.9 Comparison of fitting curves and experiment curves of stress-strain

式(13)可看作Y=dX+D，对非线性阶段的数据点进行最小二乘法拟合即可得到最终参数c和d，代入式(12)即可求得最终表达式；再利用混凝土结构设计规范[26]中的单轴拉伸应力-应变本构关系即可求得应力-应变曲线。

图9为应力-应变的拟合曲线与试验曲线对比，观察图9可以看出三种方法得到的结果均与试验结果吻合良好，进入非线性阶段后曲线斜率均呈减小趋势，到达峰值点时斜率接近为0。由此可见三种拟合方法对混凝土拉伸状态的上升段曲线都能起到良好的预测作用。

3.5 裂缝扩展长度与荷载之间的关系

获得裂缝口张开位移(w)曲线原理示意图如图10所示，在试验加载过程中，在中心预制切口上下5 mm位置处绘制两条水平线，将上方水平线Y方向位移减去下方水平线Y方向位移，差值即为w。图11为不同荷载下试件w随宽度方向的变化曲线。

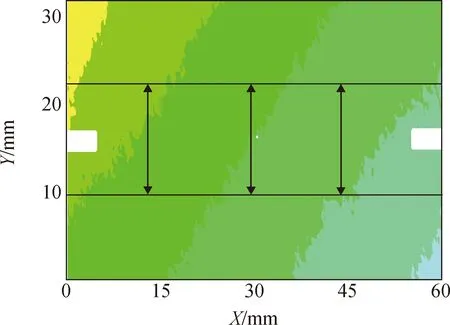
图10 获得w曲线原理示意图Fig.10 Schematic diagram for obtainig w curves

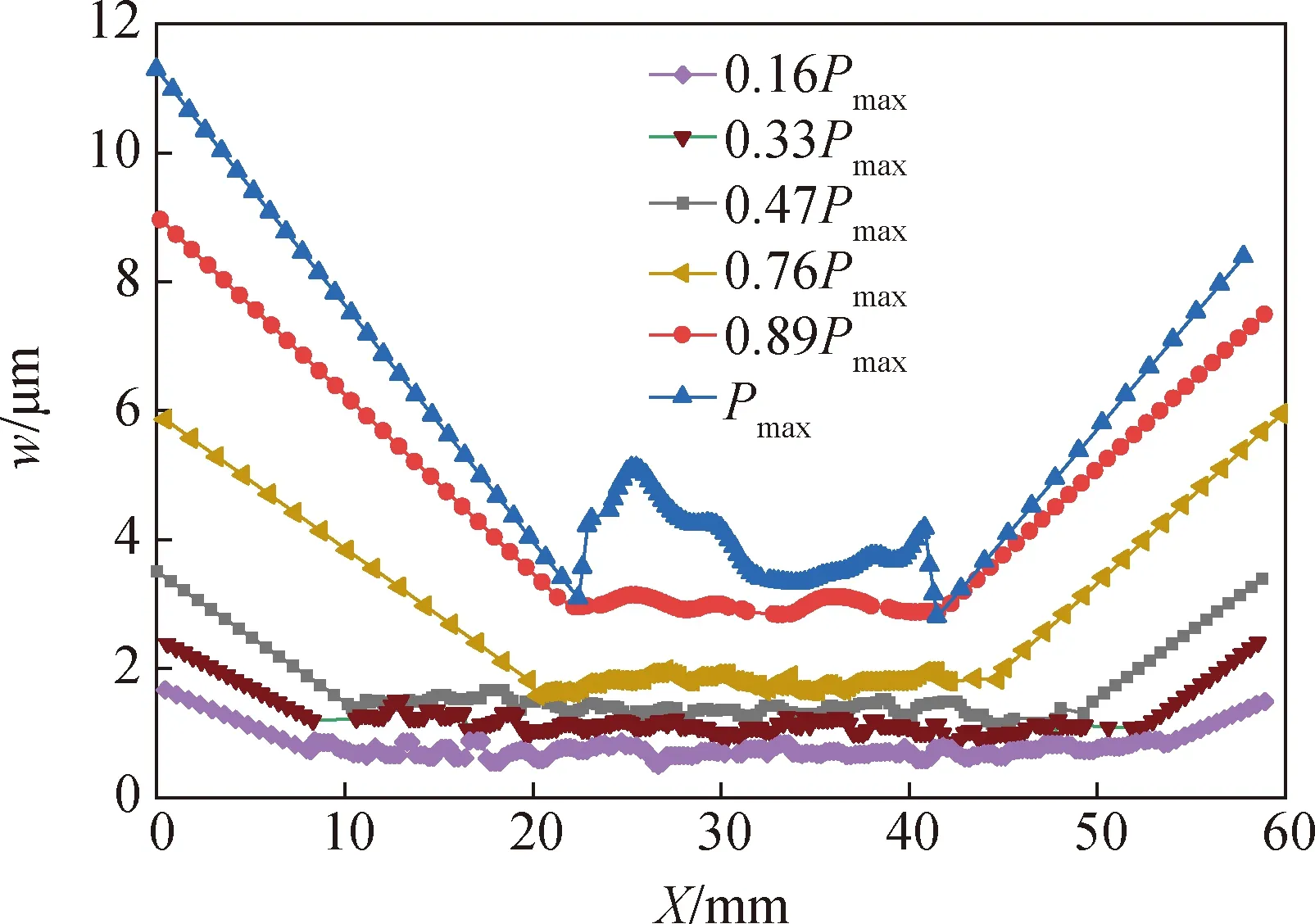
图11 试件w随宽度方向的变化曲线Fig.11 Change curves of specimen w with width direction

将图11分为三个区域：左侧裂缝区、右侧裂缝区和中部平稳区，研究整个拉伸断裂过程中P/Pmax(Pmax为峰值荷载)与平稳区w以及左右裂缝长度lp的关系。平稳区w曲线以及各阶段示意图如图12所示，讨论平稳区的w随P/Pmax的变化。当荷载处于0.16Pmax～0.76Pmax时，平稳区w与荷载呈线性关系，此时w<2 μm;当0.76Pmax2 μm，可以判断在此阶段内，混凝土内部出现了开裂，且认为此时刻是试件的理论起裂时刻，此时试件产生的塑性损伤使得其抵抗变形能力下降，这与上述讨论得到的初裂点(0.82Pmax)结果相近。综上所述可以认为：当平稳区的w<2 μm时,试件没有起裂，当w>2 μm时，试件出现开裂。

左右区域裂缝长度lp随P/Pmax变化如图13和图14所示，可以发现由于预制切口应力集中的存在，左右两端口率先起裂，该时间点并非试件的理论起裂时刻。加载中后期即荷载处于0.47Pmax～Pmax时，左右两端裂缝长度随着荷载的不断增大，裂缝长度变化速度均越来越慢，出现了相似规律，最终左端裂缝长度扩展至大约18 mm，约为韧带长度的36%，右端裂缝长度扩展至大约14 mm，约为韧带长度的28%，裂缝长度左端约为右端的1.29倍，这是混凝土内部骨料分布不均匀导致左右裂缝长度不等。

同理研究平稳区的长度l随P/Pmax的变化，结果如图15所示，可以看到平稳区的长度自加载开始逐渐减小，由约46 mm减小到约18 mm，且变化速度随着荷载的增加不断加快，这是由于混凝土的不断损伤，中部微裂缝不断发展，产生了无法恢复的裂缝，混凝土的承载能力不断下降，从而使平稳区长度下降速度加快。

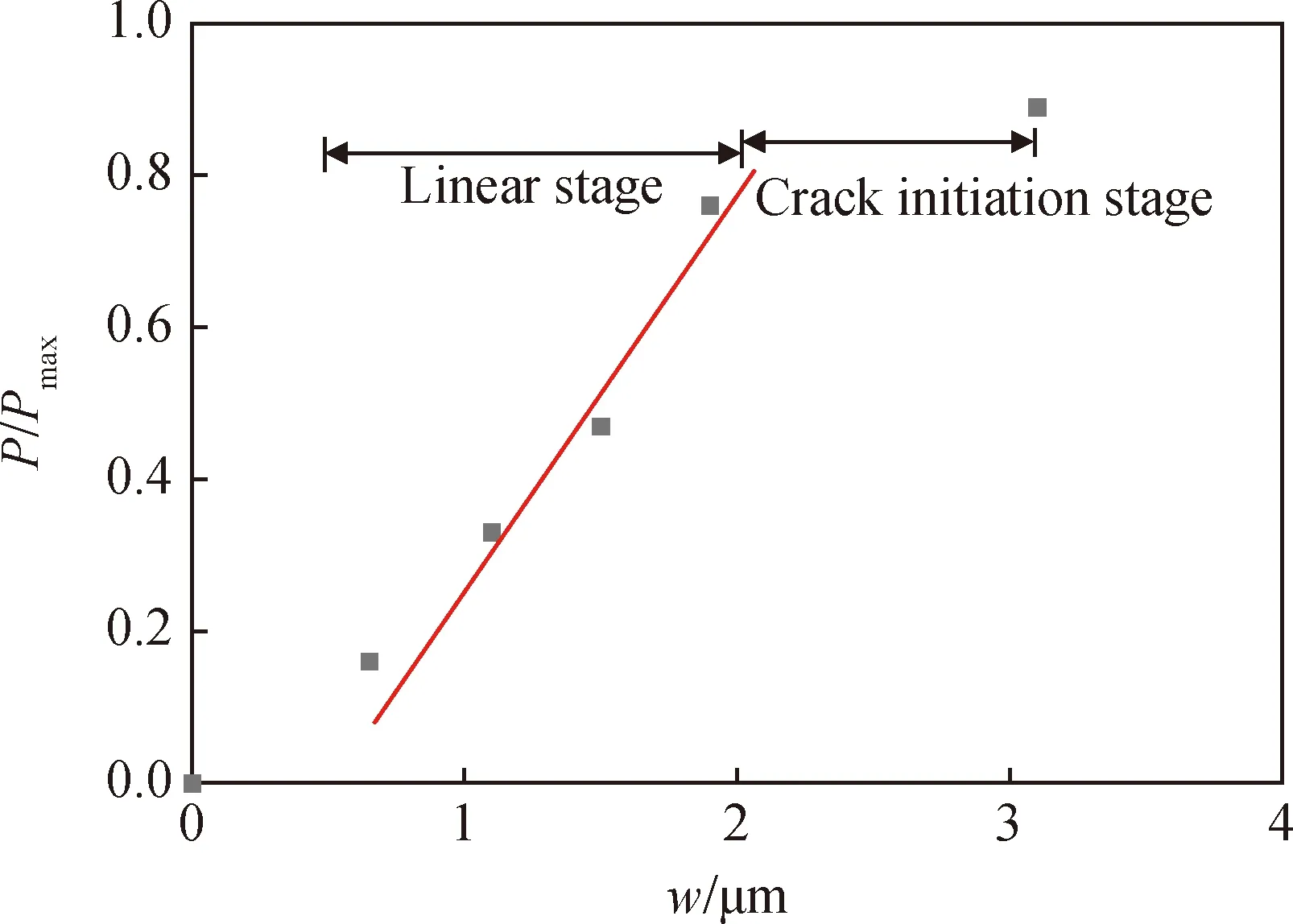
图12 平稳区w曲线以及各阶段示意图Fig.12 w curve in stable zone and schematic diagram of each stage

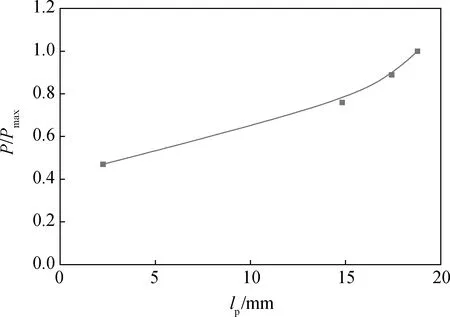
图13 试件左端裂缝长度曲线Fig.13 Left crack length curve of specimen

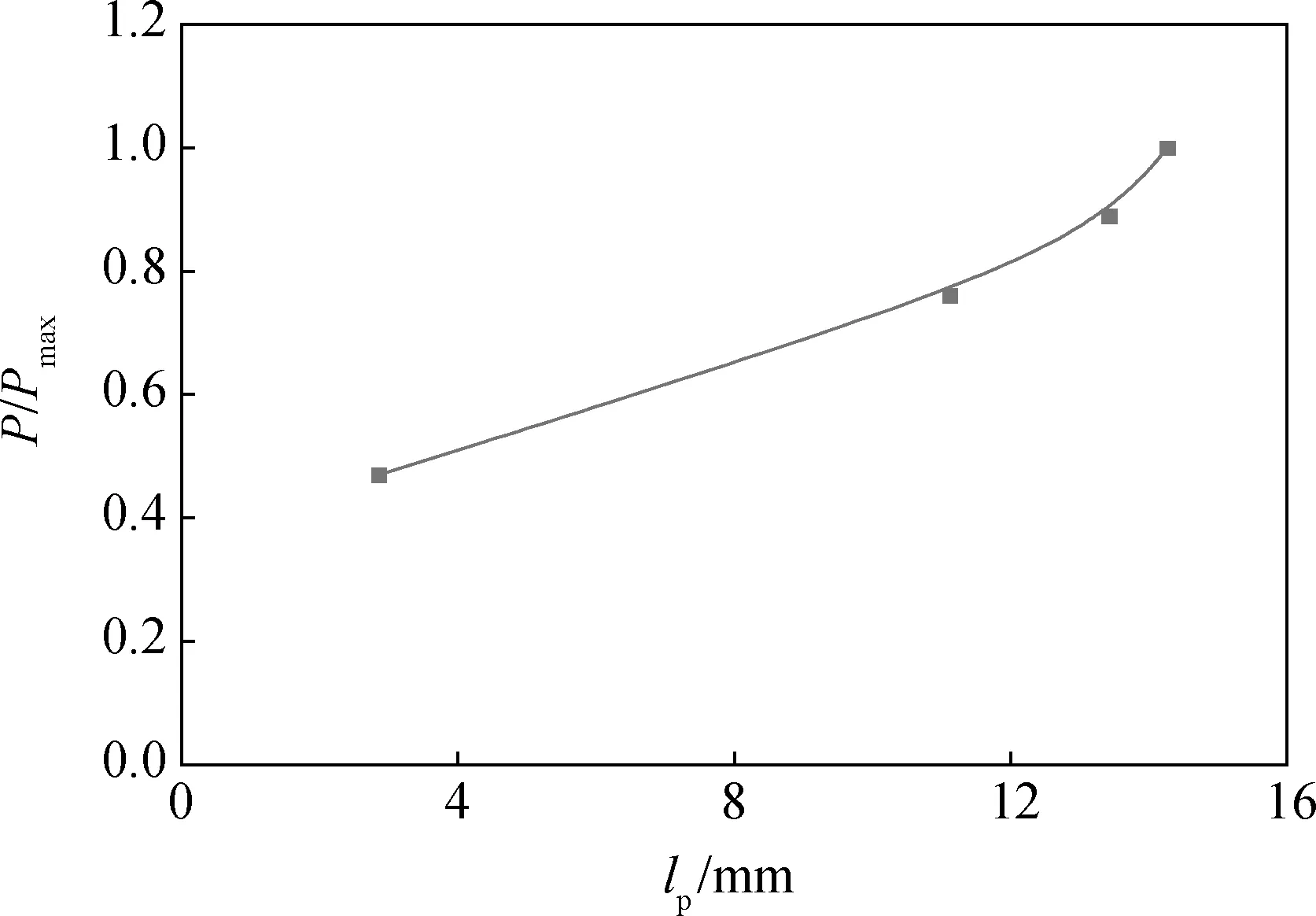
图14 试件右端裂缝长度曲线Fig.14 Right crack length curve of specimen

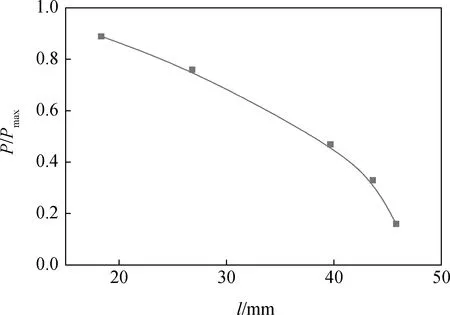
图15 试件平稳区长度曲线Fig.15 Length curve of specimen in stable zone

3.6 裂纹扩展规律

棱柱体试件ESPI位移云图和试件最终破坏图如图16所示。由于混凝土的预制切口的存在，切缝尖端会出现应力集中，随着荷载的逐步增大，应力集中处附近首先会出现微裂缝，如图16(a)所示。混凝土材料中粗细骨料的分布具有随机性以及离散型，在裂纹扩展过程中，裂纹前端可能是水泥基体或者是骨料，为了绕过骨料，裂缝轨迹会成为一条曲线，且因存在偏心，裂纹扩展是不对称的，有一边的裂纹张开位移可能会大于另外一边。随着荷载的增大中心区域微裂缝也开始发展，在扩展过程中会有次生裂纹产生，随着裂纹的扩展，混凝土中积攒的能量得到释放，其中只有主裂缝会进一步进行扩展,结果如图16(b)所示，最后中间部分微裂缝与左右两侧预制切口处的裂缝在不断扩展下汇聚一处成为宏观贯穿裂缝，当主裂缝扩展成为贯穿裂缝时，混凝土试件断裂,如图16(c)所示。

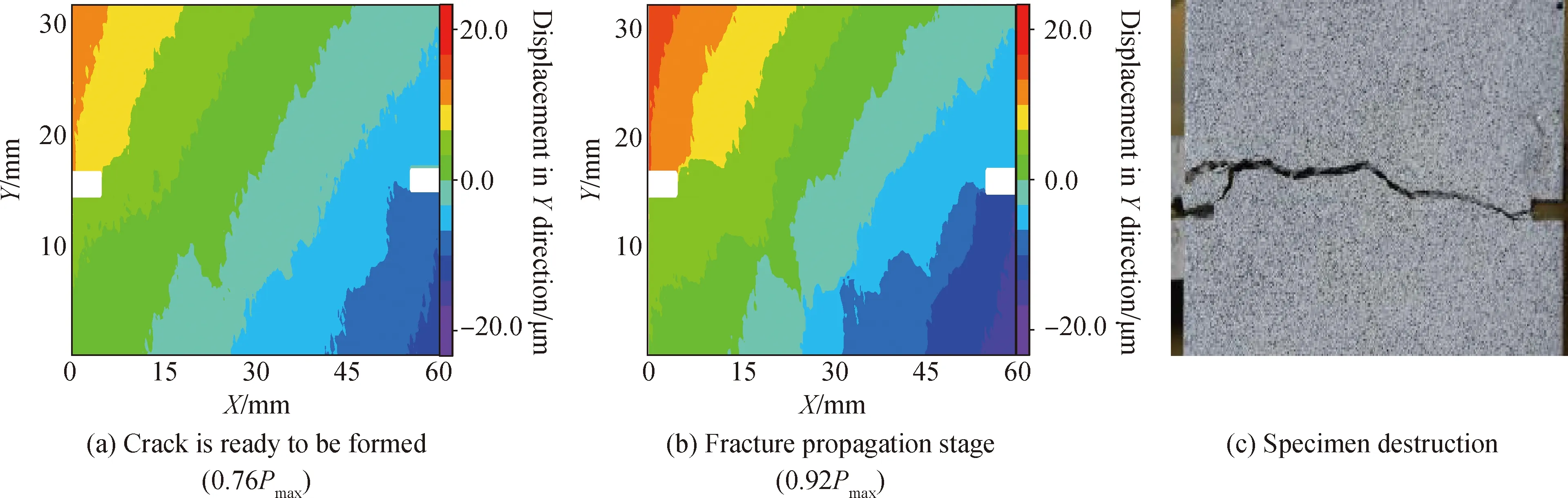
图16 0.76Pmax和0.92Pmax的位移云图与试件最终破坏图Fig.16 0.76Pmax and 0.92Pmax displacement cloud and specimen destruction chart

4 结 论

本文采用ESPI技术对带预制切口的C80高强混凝土棱柱体试件在单轴拉伸状态下的断裂特性进行了研究，得到以下结论：

(1)通过ESPI技术和夹式位移计得到的P-CMOD曲线对比，两者数据基本吻合。峰值应力处CMOD约为11 μm，表明了ESPI技术测量结果的精确性。

(2)计算得到本次试验中混凝土的各项断裂参数，其中初裂点应力约为峰值应力的82%，稳定扩展阶段断裂能GFS约为24.71 N/m，弹性模量E约为34.53 GPa与圆柱体试件所测结果34.06 GPa接近，起裂韧度KIc约0.41 MPa·m1/2。

(3)使用两个拟合公式对试验数据进行了拟合，并与混凝土结构设计规范提出的本构关系相比对，结果表明两个拟合公式均能达到较好拟合效果。

(4)通过w曲线得出理论起裂时刻，当平稳区w<2 μm时试件没有起裂，当w>2 μm时出现起裂；左右两端裂缝长度随荷载变化出现相似规律，混凝土内部骨料分布不均匀造成两端裂缝扩展长度不等；在峰值荷载下，左端裂缝长度约为18 mm，右端裂缝长度约为14 mm，平稳区长度约为18 mm。

(5)通过ESPI位移云图分析混凝土裂纹扩展的全过程，初始裂纹始于左右两端预制切口，随着荷载的增大，平稳区的裂纹出现并且逐步扩展，最后同两侧的裂纹汇聚一处成为贯穿裂纹，造成试件破坏。