基于量子多元宇宙算法的磁光成像增强

卢 慧

(商丘职业技术学院,河南 商丘 476000)

1 引 言

磁光成像属于可视化无损检测技术,能对物体表面及亚表面进行缺陷检测。当偏振光通过磁场发生旋转,角度偏差即可判断物体的缺陷,具有响应快等优点[1],被广泛应用在自动化检测领域,如工业铸锻焊件、激光焊接焊缝检测等。

磁光成像的磁场激励分为直流电、交流电两种形式,直流电产生磁场的涡流小、设备要求低,但电量消耗大,获得缺陷信息量小；交流电产生磁场成像信息量丰富、电耗低,但较深的缺陷检测困难。磁光成像在传输过程中易受各种干扰,出现清晰度、对比度较低现象,容易把关键性的图像信息丢失,通过增强处理,使得图像能够显现更多的细节信息[2]。目前对磁光成像增强方法主要有:直方图均衡化(Histogram Equalization,HE)方法对焊缝图像进行变换[3],获得的灰度直方图能将较大的灰度区域伸长,较小区域的灰度压缩,提高焊缝图像的对比度。改进模糊增强算法(Improved Fuzzy Enhancement,IFE),通过连续分段模糊算法,使低灰度区域像素灰度值更低,高灰度区域像素灰度值更高,提高像素的区分度[4]。HSI颜色空间和引导滤波(HSI Color Model and Guided Filter,HSICMGF)的增强算法,像素自变换将原始灰度图像转换至HSI颜色空间,能够得到对比度更高和层次感更强的图像[5]。限制对比度自适应直方图均衡(Contrast Limited Adaptive Histogram Equalization,CLAHE)通过限制局部直方图的高度来限制局部对比度的增强幅度,从而限制噪声的放大及局部对比度的过增强[6]。卡尔曼滤波结合径向基函数神经网络(Kalman filtering compensated with RBF neural network,KFRBFNN),卡尔曼滤波技术可补偿焊缝跟踪误差,神经网络可以抑制发散滤波,提高系统的鲁棒性[7]。自适应中值滤波(Adaptive Median Filtering,AMF)算法滤除焊缝磁光图像噪声,结合小波变换图像增强技术,能进一步突出焊缝过渡带边缘特征[8]。

以上研究方法未考虑磁光成像时形成的磁畴,仅按照图像增强方法对磁光成像处理,导致增强效果不明显。为了减少磁光成像时磁畴造成的干扰,本文采用量子多元宇宙算法(Quantum Multiverse,QM),使得磁光成像增强效果较清晰。

2 磁光成像原理

当铁磁工件被磁化后,材料表面或内部缺陷在表面形成漏磁场,利用法拉第磁旋光效应[9-11],偏振光在垂直磁场作用下产生旋光效应,光发生的偏振角度以及方向包含了焊接处的信息,磁光传感器接收检偏器检测的光,显示磁光成像,从而直观、可视化地实现了表面及亚表面疲劳裂纹无损成像检测。法拉第磁光效应为:

(1)

当铁磁材料未加磁场时,偏振光产生成像光强I0为:

I0=E2cos2(φ)

(2)

式中,E为入射线偏振光振幅,φ为检偏器与磁光传感器方向夹角,I0对应磁光成像的成像区域。

当铁磁材料加磁场时,偏振光产生成像光强为:

(3)

式中,IN、IS为焊缝两端N极和S极所对应的光强,分别对应磁光成像的较亮、较暗区域。

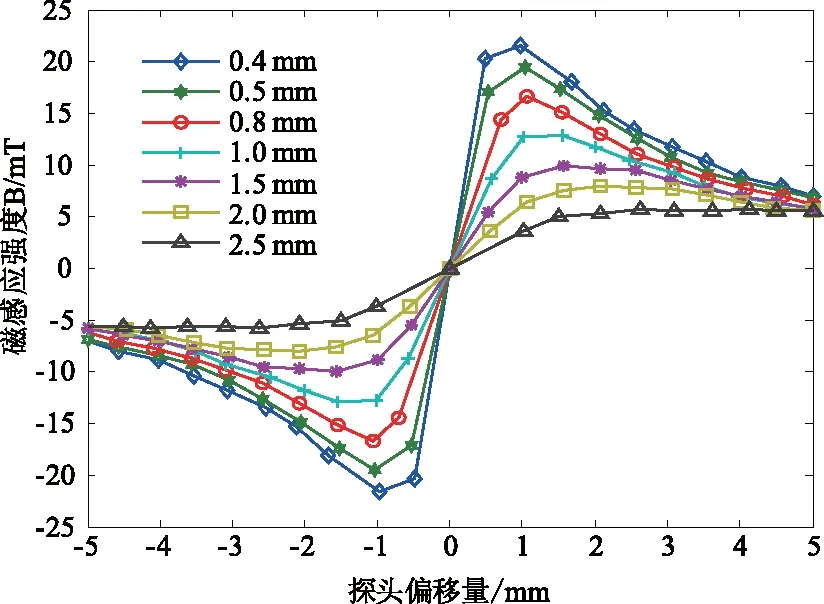
由于φ<900,I0、IN、IS之间的关系为:IS

(a)磁光成像

图1 焊缝磁光成像Fig.1 Weld magneto optic image

在图1(a)焊缝磁光成像区域中,成像较亮部分为磁场的N极,在图1(b)中表现为像素灰度值较大,对应为焊缝边缘部分；成像较暗部分为磁场的S极,在图1(b)中表现为像素灰度值较小,对应为焊缝边缘部分；介于明、暗之间的过渡区域为焊接区域,因此焊缝磁光成像的像素灰度值大小与焊缝亮度成正比,像素灰度值越大则焊缝越亮,即通过焊缝的磁场偏振角越大,使得磁光传感器越易获得焊接处的信息。

3 量子多元宇宙算法进行磁光成像增强

3.1 量子多元宇宙算法

3.1.1 基于多虫洞的多元宇宙空间结构模型

目前多元宇宙算法空间结构模型只是白洞向黑洞移动,方向单一,导致算法后期存在盲目性,无法提高算法的全局优化能力。为了使宇宙中的物质移动具有多样性,设计多元宇宙空间多虫洞结构模型,增加虫洞的数量,同时也加速宇宙的膨胀,如图2所示。

图2 多元宇宙空间多虫洞结构模型Fig.2 Multi wormhole structure model of multiverse space

在图2中,随机存在若干黑洞、白洞,黑洞为实心球形,白洞为空心球形,每个白洞和黑洞的周围存在多条虫洞,其中连接实线为真实虫洞,连接虚线为虚拟虫洞,连接实线的真实虫洞只能进行白洞到黑洞的物质转移,白洞宇宙物质会利用虫洞进行正向随机搜索；连接虚线的虚拟虫洞只能进行黑洞到白洞的物质虚拟性转移,即黑洞里有部分物质只能通过虚拟虫洞转移到白洞,宇宙黑洞物质会利用虚拟虫洞进行负向随机搜索。这样在多虫洞结构下,每一轮迭代进化增加了多元宇宙空间物质转移媒介的多样性,正负双向随机搜索性从而加速宇宙的进化,易获得最优宇宙。

3.1.2 基于动态自适应的宇宙旅行距离率

宇宙运行前期需要较大的旅行距离率以便快速到达最优宇宙周围,后期需要较小的旅行距离率以便快速在最优宇宙周围局部深度开发。根据迭代次数L设计动态自适应宇宙旅行距离率(Traveling Distance Rate,TDR):

(4)

宇宙旅行距离率TDR其变化如图3所示。

图3 宇宙旅行距离率变化Fig.3 Variation of cosmic travel distance rate

从图3可以看出,选择因子越小宇宙旅行距离率TDR变化越平缓,利于前期快速寻优,选择因子越大宇宙旅行距离率TDR变化越陡峭,利于后期精细寻优,综合考虑,本文选择λ=3。

3.1.3 虫洞存在概率

为了提高宇宙物体转移速率[12],需要增加虫洞存在概率(Wormhole Existence Probability,WEP),利用WEPmax、WEPmin值,非线性设计虫洞存在概率:

(5)

这样在迭代前期增加宇宙物体的转移速度利于大范围搜索,迭代后期减少宇宙物体的转移利于局部小范围搜索。

3.1.4 宇宙位置更新

为了使得宇宙种群在迭代过程中保持多样性,宇宙会不断向当前最优宇宙移动,通过模运算和变异策略更新宇宙位置如下:

(6)

3.2 基于量子机制的多元宇宙优化

3.2.1 宇宙量子化

宇宙量子化过程为:假设宇宙可同时具有黑洞和白洞的特性,α、β为宇宙黑洞和白洞状态概率,0、1状态为宇宙黑洞和白洞状态概率幅,则宇宙量子化比特状态由0、1或者叠加态构成:

|φ〉=α|0〉+β|1〉

(7)

式中,|α|2+|β|2=1,|α|2、|β|2为|φ〉处于状态0和状态1的概率。

3.2.2 自适应量子旋转门调整

量子机制的多元宇宙进化主要利用量子旋转方向和旋转角度大小改变实现,旋转方向调整为:

(8)

旋转角度大小采用线性增大方法:

(9)

式中,θmax、θmin分别为旋转角度最大值、最小值,θo为当前最优量子宇宙的旋转角。这样量子宇宙在自适应量子旋转门调整状态下可快速进行更新。

3.3 磁光图像增强

3.3.1 磁畴区域计算

铁磁材料自身特性存在磁畴现象,特别是当加磁场时磁畴易产生微小纹理,在磁光成像时容易被误认为缺陷,导致误判发生,因此在磁光成像中需要把磁畴消除。磁畴在磁光图像I(x,y)中的主要表现形式为随机散落的点块,因此把磁光图像M×N均等分P×Q个块,每个块大小为m×n,计算块单元内目标像素点和基本单元内总像素点的比例R(x,y):

(10)

式中,R(x,y)为第(X,Y)个图像块内目标像素点和总像素点的比例。若R(x,y)大于某个阈值κ,则该像素块标记为磁畴图像块[13],为了能够消除微小磁畴区域的影响,本文设置κ=0.15。

3.3.2 引导滤波

由于激励源为低频交流信号,因此磁光图像中磁畴信息变化丰富,通过引导滤波算法减少磁畴对磁光成像的影响:

qk=ξ1Ik+ξ2,∀k∈wz

(11)

式中,qk为输出矩阵中像素点k的灰度值；Ik为引导矩阵中像素点k的灰度值；wz为滤波窗口；wz为窗口中心；ξ1、ξ2为常系数。

由于引导矩阵存在梯度,为了使得输出矩阵也保留梯度[14],求导得:

(12)

为了使输入矩阵与输出矩阵的差别最小,设置代价函数:

(13)

求得常系数值:

(14)

3.3.3 增强函数选择

arctan函数能对磁光成像区域增强而非背景区域[15],从而抑制背景灰度值。

3)当需要支架前移时，支架立柱油缸、护帮油缸卸压，油缸收缩，支架立柱收缩，完成支架的降架过程，顶梁油缸、护帮油缸卸压，伸缩梁向内收缩，完成支架的收缩过程。

(15)

量子多元宇宙算法的目标函数:

(16)

算法流程:

①输入待增强图像,多元宇宙初始化；

②计算量子多元宇宙的目标函数值；

③量子多元宇宙位置更新；

④比较宇宙当前位置和对应的目标函数值,若当前目标函数值优于历史最优目标函数值,将此宇宙当前的位置作为最优位置,否则保持历史最优值和目标函数值不变；

4 实验结果及分析

实验PC配置为CPU3.0 GHz、内存8 GB,集成显卡,Matlab 7.0编程实现仿真。选用铁磁材料为增强铁芯,磁光传感器采样速率为22幅/s,特斯拉计高精度可达0.01 MT,量程为0～2400 MT,横向霍尔探头探测焊接处磁强,磁光成像传感器发光二极管阵列为高功率光源,波长590 nm,光强传输比较高,可避免不同波长偏转角度不一致造成的图像模糊,提高图像清晰度,有利于法拉第效应旋转角度的量化和成像对比度。磁场激励电源综合考虑直流和交流的优势,采用低频交流。

4.1 焊接处磁感应强度变化规律分析

大小为25 mm×20 mm的磁光薄膜表面覆盖了镜面涂层,焊缝宽度为0.8 mm,霍尔探头从其中心按0～5 mm的距离逐渐增加,电磁铁距离,分别接通5 V、10 V、15 V、20 V的交变电压,交变电流大小为1 A,交变频率为50 Hz,磁光成像设备与工件的距离设置成0.4 mm、0.5 mm、0.8 mm、1.0 mm、1.5 mm、2.0 mm、2.5 mm,获得的焊接处磁感应强度变化曲线如图2所示。

从图4可以看出,霍尔探头获得的磁感应强度变化随着交变电压的增加而变大；霍尔探头离焊缝中心越远,则磁感应强度越小；磁感应强度在焊缝中心呈现对称分布,最小值在焊缝中心处,即磁场N级、S级交接处；磁感应强度在磁场N级出现波峰极值,

(a)5 V

(b)10 V

(c)15 V

(d)20V图4 焊接处磁感应强度变化曲线Fig.4 Variation curve of magnetic induction intensity at welding joint

磁感应强度在磁场S级出现波谷极值；波峰极值、波谷极值出现位置以焊缝中心为对称轴,距离焊缝中心小于1 mm,因此霍尔探头最佳位置在距离焊缝中心0.6 ～1 mm处,此时磁光成像效果最好。

4.2 磁畴在不同交流电压下对磁光成像的影响

固定霍尔探头位置离工件焊缝中心0.8 mm处,分析磁畴在不同交流电压下对磁光成像的影响,电磁铁交变电压分别接通5 V、10 V、15 V、20 V,交变频率为50 Hz,磁光传感器记录此时的成像结果,如图5所示。

(a1)磁光成像

(a2)三维直方图

(b1)磁光成像

(b2)三维直方图

(c1)磁光成像

(c2)三维直方图

(d1)磁光成像

(d2)三维直方图图5 不同交流电压的磁光成像及直方图Fig.5 Magneto optic imaging and histogram of different AC voltages

从图5可以看出,随着低频交流电压的增加,生成的磁光成像清晰度逐渐增加,同时工件的磁畴特性表现的越明显,这是因为低频交流电压的增加使得磁场强度变大,磁场强度使得磁光成像区域的亮度由暗到明变化越明显,因此磁光成像清晰度较清晰；工件的磁畴范围随着磁场强度增加逐渐增大,当磁场强度较小时,磁畴的磁化向量都会向磁场方向转动；当磁场强度变大,磁畴壁向外扩张,此时磁畴相当于增大自己的体积,逐渐使得磁畴壁向外扩张的纹理显示更明显,当磁畴壁扩张到极限时,磁畴的方向将与外加磁场的方向一致。因此交流电压越大,磁光成像越清晰,磁畴也越明显。

4.3 不同算法磁光成像增强分析

将低频交流电压20 V获得磁光图像进行增强,涉及的算法有:HE、IFE、HSICMGF、CLAHE、AMF、QM,各种算法获得的结果如图6所示。

(a) 磁光图像

(b) 不同算法对磁光图像1增强

(c) 不同算法对磁光图像2增强图6 不同算法磁光成像增强分析Fig.6 Magneto optic imaging enhancement analysis of different algorithms

从图6各种算法磁光成像增强可以看出,QM算法对磁光成像增强过程种引导滤波减少了磁畴干扰,突出了焊接信息,同时arctan函数对磁光成像区域增强而非背景区域。其他算法消除磁畴不明显,可视性低。

采用图像信息熵En评价增强效果,En越大则图像中含有的信息量越多,表现的细节越清晰。

(17)

式中,p(g)表示图像中灰度值为g的像素个数与图像中所有像素之比。

对图6各种算法的增强评价指标En如图7所示,各种算法进行30次实验。

从图7可以看出,QM算法对磁光图像增强的清晰度显著性提高,En值最大,其平均值为7.55,HE算法的En平均值为6.11,IFE算法的En平均值为6.30,HSICMGF算法的En平均值为6.58,CLAHE算法的En平均值为6.69,AMF算法的En平均值为7.01,QM相比HE、IFE、HSICMGF、CLAHE、AMF分别增加了23.57 %、19.84 %、14.74 %、12.86 %、7.70 %。

图7 各种算法增强评价指标EnFig.7 En evaluation Enindexes of various algorithms

均方误差(Mean Square Error,MSE):

(18)

对图6各种算法的增强评价指标MSE如图8所示,各种算法进行30次实验。从图8可以看出,QM算法对磁光图像增强的MSE最小,其平均值为3.28,HE算法的MSE平均值为5.23,IFE算法的MSE平均值为4.94,HSICMGF算法的MSE平均值为4.62,CLAHE算法的MSE平均值为4.27,AMF算法的MSE平均值为3.95,QM相比HE、IFE、HSICMGF、CLAHE、AMF分别减少了37.28 %、33.60 %、29.00 %、23.19 %、17.17 %。

图8 各种算法增强评价指标MSEFig.8 MSE evaluation indexes of various algorithms

5 结 论

(1)磁感应强度变化随着交变电压的增加而变大；霍尔探头离焊缝中心越远,则磁感应强度越小；磁感应强度在焊缝中心呈现对称分布,最小值在焊缝中心处,即磁场N级、S级交接处。

(2)随着低频交流电压的增加,生成的磁光成像清晰度逐渐增加,同时工件的磁畴特性表现的越明显。

(3)量子多元宇宙算法使磁光成像增强轮廓清晰,减少了磁畴干扰,便于分析,为磁光成像增强提供了一种新思路。