SαS分布噪声模型下激光信号互相关时延估计

李丰君,徐广平,耿 林,霍晓培

(华北光技术研究所,北京 100015)

1 引 言

脉冲式激光测距是由激光器对被测目标发射一个脉冲,然后由光电接收系统接收反射回来的脉冲,通过测量脉冲往返的时间来算出目标的距离。由于脉冲激光发散角小、瞬时功率大、无合作目标、速度快和实现简单,因此其应用领域非常广泛[1-2]。

相关算法是一种经典的检测信号和处理信号的手段,常常在在信号的处理中,对信号进行检测、识别和提取[3]。然而,在实际测距中接收到的脉冲信号受到大气噪声和电路噪声的影响,大大影响了相关算法的效果。在实际测距中的大气噪声可认为是由许多具有随机相位幅度、形状不固定的脉冲叠加而成,在幅度上存在严重的“重尾”特征,具有非高斯特性[4]。脉冲噪声的抑制有多种途径,如自适应滤波、最小分散系数准则、最大相关熵准则、对数最小平均次幂准则等[5],但这些方法在应用上比较复杂。因此,需要提出一种不需要先验信息、结构简单、适用范围大的抑制脉冲噪声算法。本文采用Sigmoid非线性函数对脉冲噪声进行抑制。

本文首先对接收到的激光回波信号进行建模,然后介绍基于Sigmoid函数的互相关时延估计算法,最后对该算法进行仿真,分析不同k值对时延估计的影响。

2 模型建立

2.1 激光发射脉冲模型

本文所需的激光发射脉冲系统是在保证安全发射功率(平均发射功率小于1MW)的条件下,脉冲宽度为纳秒量级的钟形脉冲信号。对其进行建模:

(1)

其中,s(t)激光发射脉冲信号;A是激光脉冲幅值;u是激光脉冲峰值位置;b是纳秒量级激光脉冲宽度;t是时间。图1为激光发射脉冲模型。

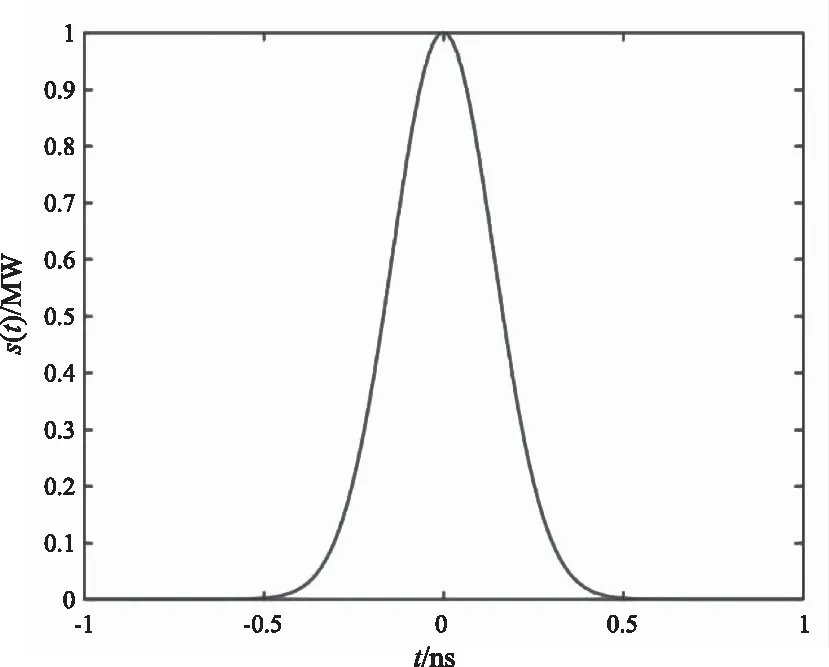
图1 激光发射脉冲模型Fig.1 The model of laser pulse

2.2 SαS分布噪声模型

1925年,Paul Levy在研究广义中心极限定理时给出Alpha稳定分布的概念[6]。1933年,M.shao和C.Nikias首次将Alpha稳定分布引入信号处理领域[7],并掀起Alpha稳定分布在工程领域的研究热潮。2000年后,Alpha稳定分布广泛应用于各类高斯、非高斯噪声的建模[8]。Alpha稳定分布是唯一满足广义中心极限定理的分布,与高斯分布相比,Alpha稳定分布概率密度函数拖尾更加厚重。激光回波信号中主要受到大气噪声、光电探测器和前置放大电路的噪声影响,罗忠涛在2018年录取大气噪声数据并白化滤波后的噪声分布检验和PDF对比表明,其幅度近似服从SαS分布[4],SαS(Symmetric Alpha-Stable)模型是Alpha稳定分布噪声模型中应用最广泛的一类模型,本文选择SαS分布噪声进行建模。

由于SαS分布的概率密度函数没有封闭的表达式,但是可以用给出统一的特征函数,SαS分布的特征函数如下所示[9]:

ψα,γ(ω)=exp(-γ|ω|α)

(2)

式(2)由α、γ两个参数描述:

1)特征指数α:α ∈(0,2],一般在1～2取值,描述概率密度函数(PDF)的拖尾厚度。α越小,PDF拖尾越厚,如图2所示,并且脉冲特性越频繁,如图3所示；α=2时,Alpha稳定分布和高斯分布完全相同,可以认为高斯分布是 Alpha稳定分布的一个特例。

图2 不同α值下SαS分布的PDFFig.2 PDF of SαS distribution with different α

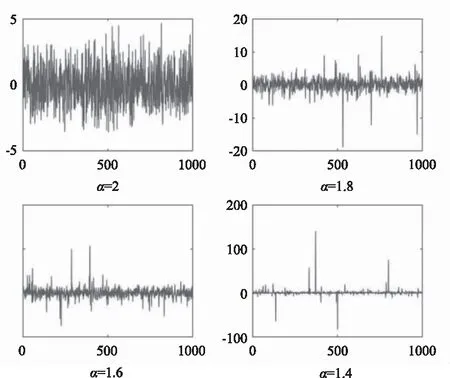
图3 不同α值下的SαS分布噪声模型Fig.3 Noise model of SαS distribution with different α

2)分散系数γ∶γ ∈(0,+∞),描述Alpha稳定分布相对于中心的分散程度。

2.3 回波信号模型

接收到的激光回波离散信号模型为:

x(n)=λs(n-d)+v(n)

(3)

其中,x(n)为探测器接收到的回波信号;s(n)为激光发射脉冲;d为激光器发出信号到探测器接收到信号的时间间隔;λ为衰减因子;v(n)为噪声,服从SαS分布。

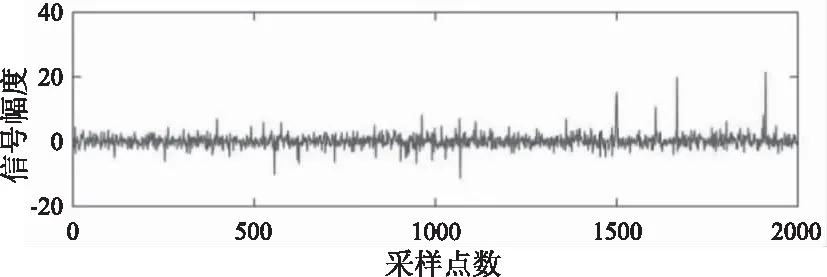
图4 回波信号模型Fig.4 Echo signal model

3 基于Sigmoid函数的互相关时延估计算

3.1 基于Sigmoid函数的信号处理

采用式(4)对回波信号进行处理,该函数可以将回波信号的映射在(-1,1)的区间(如图5),对回波信号中较大的值做非线性变换,对较小的值做线性变换,从而达到抑制较大脉冲噪声和保留有用信号的效果[11]。

f(x(n))=2S(x(n))-1

(4)

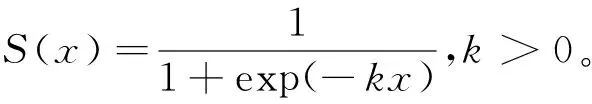
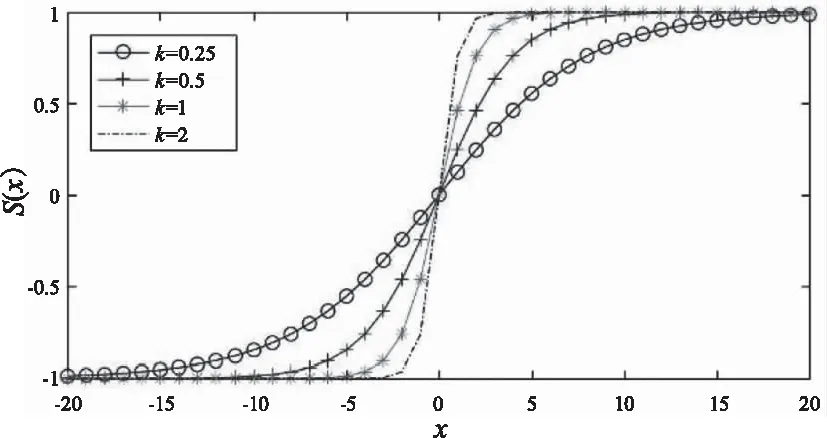
图5 不同k值下的Sigmoid函数Fig.5Sigmoid function of different k

3.2 互相关时延估计

激光器发射的含噪激光脉冲信号和探测器接收到的含噪回波信号如下式所示:

(5)

式中,x1(t)是激光器发射的含噪激光脉冲信号;x2(t)是探测器接收到的含噪回波信号;s(t)是激光发射脉冲信号;d是需要估计的延迟时间;λ是衰减因子;v2(t)是回波信号中的噪声,用SαS分布噪声模型描述。

x1(t)和x2(t)的互相关函数表示为:

R12(τ)=E[x1(t)x2(t+τ)]

=E{[s(t)+v1(t)][λs(t-d+τ)+v2(t+τ)]}

=λE[s(t)s(t-d+τ)]+E[s(t)v2(t+τ)]+

λE[v1(t)s(t-d+τ)]+E[v1(t)v2(t+τ)]

由于

E[s(t)v2(t+τ)]=0

E[v1(t)s(t-d+τ)]=0

E[v1(t)v2(t+τ)]=0

因此

R12(τ)=λE[s(t)s(t-d+τ)]

=λRss(τ-d)

由自相关的性质可知,当τ=d时R12(τ)达到最大,即:

(6)

4 仿真结果与分析

4.1 基于Sigmoid函数的互相关时延估计

为了分析基于Sigmoid函数的互相关时延估计算法,下面通过matlab构造混杂SαS分布噪声的钟形脉冲回波信号。其中广义信噪比GSNR=-5,α=1.6,时间延迟d=1500,采样点数N=2000,如图6所示。

图6 GSNR=-5,α=1.6时的回波信号Fig.6 Echo signal at GSNR=-5,α=1.6

对上述回波信号(α=1.6)进行基于k=0.5的Sigmoid函数信号处理后的波形如图7所示。

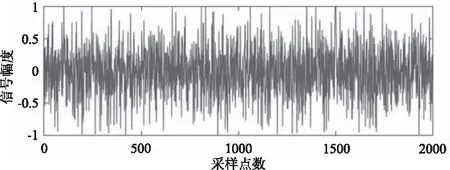
图7 经Sigmoid函数处理后的波形(k=0.5)Fig.7 Waveform after sigmoid function processing(k=0.5)

将在α=1.8、α=1.6、α=1.4 和α=1.2不同脉冲噪声强度情况下的经Sigmoid函数处理后的波形与已知激光器发射脉冲信号进行互相关仿真(GSNR=-5 dB)。

如图8所示,可以看出在时间采样点n=1500处对应峰值点,且随着脉冲强度的增大(α的增大)互相关峰值逐渐被噪声淹没,互相关峰值误判点增多,最大误判点与定位点的比值越大,时延估计性能恶化。

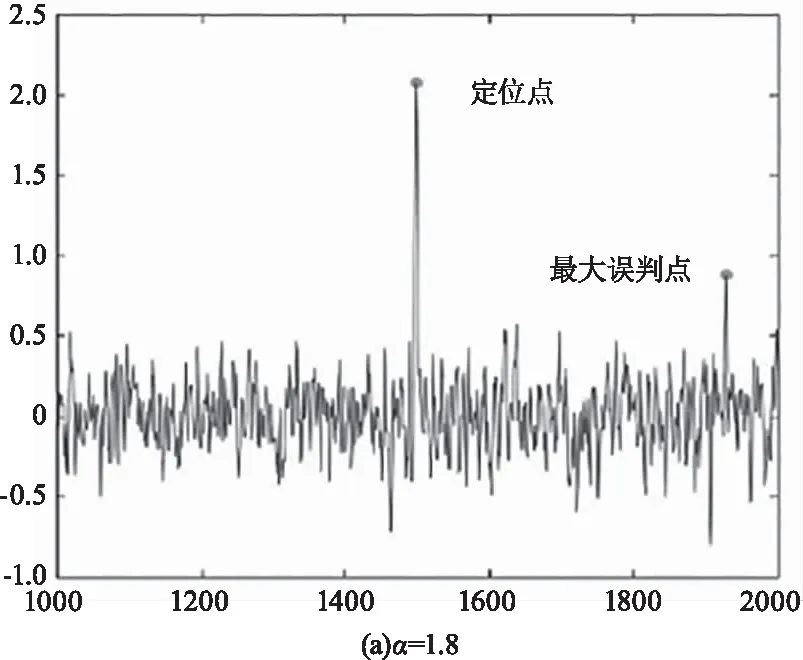
图8 不同α值下互相关时延估计结果(k=0.5)Fig.8 Time delay estimation results of different α(k=0.5)

4.2 k的取值与估计性能分析

对混杂了SαS分布噪声的钟形脉冲回波信号(α=1.6,γ=1,GSNR=-5 dB)进行不同k值下基于Sigmoid函数信号处理后的波形如图9所示。k的取值越大,对回波信号幅值的抑制越强,k的取值过大甚至会过度抑制有用信号,随之影响互相关时延估计的准确性,如图9(a)所示；k的取值过小会保留大量的噪声脉冲,造成互相关后引起过多尖峰也会影响互相关峰值判断的准确性,从而影响时延估计性能,如图9(d)所示。

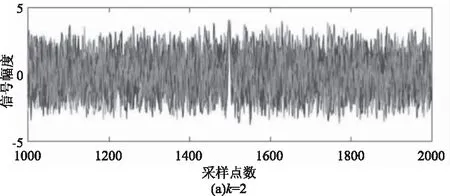
图9 不同k值下互相关时延估计结果Fig.9 Time delay estimation results of different k

最大误判点峰值与定位点峰值比的计算公式为:

(7)

其中,N表示最大误判点峰值与定位点峰值的比值；N1为最大误判点峰值；N0为定位点峰值。因此由式(7)可以看出,比值越大,时延估计性能越差,本文将N作为衡量时延估计性能优劣的参数进行分析。

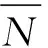
图10 与k关系的仿真散点图Fig.10 Relation diagram of k

5 总 结

本文对脉冲噪声背景下脉冲式激光测距互相关时延估计算法进行了研究。首先采用钟形脉冲模型对发射激光脉冲进行建模、采用SαS模型对脉冲噪声进行建模；然后提出了基于Sigmoid函数的互相关时延估计算法,通过检测互相关峰值位置就可以得到回波信号相对于发射激光脉冲的时延；最后对Sigmoid函数中的k值进行分析,通过大量仿真,在发射激光脉冲宽度一定时,激光脉冲幅值A与k的关系为kA≈3时,时延估计效果最好,此时的时延估计效果优于直接使用k=1的时延估计效果。

本文采用的方法结构简单,不需要噪声的先验知识；应用范围广泛,不仅可以用于高斯噪声背景下的时延估计,还可以用于非高斯背景下的时延估计。应用此算法在实际的脉冲式激光测距中并对实测结果进行分析则是下一步的研究方向。