基于BFGS算法的空间圆拟合方法

秦锋，鹿松，张振虎

(1.中国核工业集团三门核电有限公司，浙江 台州 317112； 2.上海勘察设计研究院(集团)有限公司，上海 200093)

1 引 言

工程应用中经常需要对圆形物体进行检测或建模，大多数情况下圆形物体并非水平放置，传统的平面圆拟合方法并不适用，而需要进行空间圆的拟合。空间圆无直接公式描述，基于公式拟合的方法难以实施。空间圆通常可通过空间平面与球面相截得到，故大多数空间圆拟合采用平面与球面相截法，如文献[1～4]先拟合空间平面求解空间圆所在平面法向量，然后利用球面中垂面的性质构造中垂面方程联立空间平面方程解算空间圆圆心及半径；文献[5～7]通过拟合空间平面和一个球心在空间平面上的球面并解出空间圆所在平面法向量、空间圆圆心及半径；文献[8]分别拟合空间平面及球面，然后将球心投影到空间平面计算圆心及半径。另有部分文献将空间圆拟合问题变为平面圆拟合问题，如文献[9-11]在拟合空间平面得到平面法向量后构造旋转矩阵通过坐标转换方式将空间圆变为平面圆，然后拟合平面圆得到平面圆圆心及半径，最后再通过坐标转换得到空间圆圆心；文献[12]先拟合空间平面，再将拟合点投影到空间平面上，建立误差方程并联立空间平面方程按附有限制条件的间接平差迭代求解。考虑到空间圆拟合数据中可能含有粗差，文献[13～15]在上述算法的基础上进行了改进，通过RANSAC(Random Sample Consensus，简称RANSAC)算法剔除粗差点，然后再采用上述算法求解空间圆拟合参数。

上述算法均采用两步求解，即第一步计算出空间圆所在平面法向量，第二步求出空间圆圆心及半径。本文采用一步求解，即通过Broyden-Fletcher-Goldfarb-Shanno(简称BFGS)算法一次性解算出全部空间圆拟合参数。为确保优化函数收敛至极值，给出了一种简便的空间圆拟合参数初始值计算方法。然后结合案例，与文献[1]、文献[9]中方法进行了对比，验证了本文算法的准确性和有效性。

2 数学模型及算法

2.1 空间圆拟合模型

空间圆所在平面方程可用下式表示：

ax+by+cz+d=0，s.t.a2+b2+c2=1

(1)

式中s.t.是subject to的缩写，表示受限制于某条件。

为减少参数的计算，参考球面坐标系表示方法，令：

a=cosαsinβ，b=sinαsinβ，c=cosβ

(2)

空间圆所在平面方程又可表示为：

cosαsinβx+sinαsinβy+cosβz+d=0

(3)

空间圆外一点(xi，yi，zi)，(1≤i≤n)到空间圆所在平面的法向偏差dvi可表示为：

dvi=cosαsinβxi+sinαsinβyi+cosβzi+d

(4)

假设空间圆的圆心坐标为(x0，y0，z0)，其应位于空间圆所在平面上，则有：

cosαsinβx0+sinαsinβy0+cosβz0+d=0

(5)

将式(4)与式(5)相减，得到空间圆外一点(xi，yi，zi)到空间圆所在平面的法向偏差dvi的另一种表述形式：

dvi=cosαsinβ(xi-x0)+sinαsinβ(yi-y0)

+cosβ(zi-z0)

(6)

设空间圆半径为R，空间圆外一点(xi，yi，zi)到空间圆的径向偏差dri可表示为：

(7)

则空间偏差dsi可表示为：

(8)

根据最小二乘法，以空间偏差平方和为对象构建优化函数fs：

(9)

在优化函数fs取得最小值时得到的空间圆拟合参数为最佳参数，即求解以下数学问题：

minfs(w)，w=[x0，y0，z0，α，β，R]T

(10)

2.2 BFGS优化算法

式(10)为无约束非线性最小二乘问题，根据文献[16]，解决非线性最小二乘问题常用算法有Gauss-Newton(简称GN)算法、Levenberg-Marquardt(简称LM)算法、牛顿法及拟牛顿法。GN算法对于小残量问题有较快的局部收敛速度，对于不是很严重的大残量问题，有较慢的局部收敛速度，对于残量很大的问题或非线性程度很大的问题往往不收敛。GN算法要求雅可比(Jacobi)矩阵满秩，如果不满秩，方法没有定义，而且GN算法不一定总体收敛。LM算法最早由Levenberg提出，在GN算法加入正则化参数改善矩阵条件，后由Marquardt进行了改进。该方法是一种介于梯度下降法和GN算法之间的算法，常用于求解非线性最小二乘问题，在正则化参数大时相当于梯度下降法，参数小时相当于GN算法。在GN算法中，一旦雅可比矩阵奇异的情况发生，使得算法常常收敛到一个非驻点，LM算法通过添加正则化参数显著改善了这一情况，但其并不能完全避免矩阵奇异的情况。牛顿法需要计算海森(Hessian)矩阵，但有的目标函数海森矩阵很难计算或者计算量过大，导致牛顿法应用受限。拟牛顿法通过利用目标函数和一阶导数的信息构造出目标函数的曲线近似，而不需要明显形成海森矩阵，其计算量较牛顿法小并兼具收敛速度快的优点，导致其比牛顿法更受欢迎、应用范围更广。拟牛顿法中最著名的算法为Broyden-Fletcher-Goldfarb-Shanno(简称BFGS)算法，其由Broyden[17]、Fletcher[18]、Goldfarb[19]、Shanno[20]等学者于20世纪60年代末70年代初提出，是当前最常用的拟牛顿算法。BFGS算法中校正矩阵始终保持正定性，并且算法具有超线性收敛速度，当采用不精确线性搜索时，BFGS算法还具有总体收敛性质。因此本文采用BFGS算法和Armijo不精确线性搜索策略[21]解决式(10)中的无约束非线性最小二乘问题。

首先对函数fs进行偏微分，为便于展示，令：

对各参数的偏微分如下：

(11)

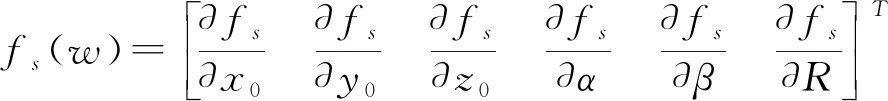
根据文献[16]，算法步骤详见以下算法1-1。

算法1-1：

步骤0，选取参数β∈(0，1)，σ∈(0，0.5)，初始点w0∈Rn，终止误差0≤ε≪1，初始对称正定阵H0(通常取单位矩阵In)，令k：=0

步骤1，计算gk=∇fs(wk)，若||gk||≤ε，停止计算，输出wk作为近似极小点。

步骤2，计算dk=-Hkgk，得到dk。

步骤3，设mk是满足下列不等式的最小非负整数m：

令αk=βmk，wk+1：=wk+αkdk

步骤4，由以下校正公式确定Hk+1

其中，sk=wk+1-wk，yk=∇fs(wk+1)-∇fs(wk)

步骤5，令k：=k+1，转步骤1。

2.3 初始值计算

函数fs为非凸函数，存在多个驻点，因此，为确保函数在迭代过程中收敛到极小值，迭代初始值需要合理选取。以下是一种较简单的拟合空间圆初始值计算方法。

将平面方程ax+by+cz+d=0两侧同除以d(d≠0)，令a′=a/d，b′=b/d，c′=c/d方程可以简化为：

a′x+b′y+c′z=-1

(12)

因方程的三个参数之间存在着线性关系，故可采用线性最小二乘解算(a′，b′，c′)T，再将解算出的(a′，b′，c′)T单位化，就可根据式(2)反算出角度(α，β)的初始值(α0，β0)。

(13)

得到空间圆圆心初始值后，就可计算出圆心到各个点的距离，然后对这些点取平均值就可以得到空间圆的初始半径R0。

(14)

2.4 空间圆拟合效果评价

空间圆拟合效果可通过均方根误差(Root Mean Squared Error，RMSE)评价。各点拟合后的法向偏差dvi、径向偏差dri及空间偏差dsi可分别用式(6)、式(7)及式(8)进行计算。空间圆拟合法向偏差均方根误差mdv、法向偏差均方根误差mdr及空间偏差均方根误差mds可根据下式计算。

(15)

3 工程算例

以激光跟踪仪测量的某设备端面圆为例，进行空间圆的拟合。采集的原始数据如表1所示。

表1 某设备端面圆测量原始数据

表2 各种算法计算结果(单位/mm)

通过表2可发现，本文算法法向误差RMSE小于文献[1]改进及文献[9]算法，说明前者算法空间平面拟合精度优于后者。对比径向误差RMSE及空间误差RMSE可发现，本文算法及文献[9]算法在径向误差、空间误差等方面均优于文献[1]改进算法。从整体比较，本文算法和文献[9]算法优于文献[1]改进算法，本文算法略优于文献[9]算法，说明本文算法可行，精度较高。

4 结 论

本文借助球面坐标表示方式构造了空间圆拟合误差函数，通过采用BFGS数值优化算法，可一步解算出所有空间圆拟合参数，改变了传统的两步拟合空间圆方法。为确保优化函数快速收敛至极值，本文还给出了一种简便的空间圆拟合参数初始值计算方法。通过案例分析与验证，本文方法精度高，迭代快，可适用于高精度的空间圆拟合。