GPS高程拟合法研究拟合区域高程异常

周复旦，戈树兵，郑波，樊振华

(徐州市勘察测绘研究院有限公司，江苏 徐州 221000)

1 引 言

GPS相对定位可以获得较高精度的两点间的大地高之差。当区域控制网中有少量重合的几何水准点，就可以计算出其他GPS点的正常高，这种计算方法一般称为高程拟合法[1]。由于正常高是以似大地水准面为基准的，大地高是以椭球面为基准的[1]。所谓高程拟合实际上是用一个数学曲面来拟合区域似大地水准面，拟合精度的高低取决于水准点与GPS重合点的精度、密度与空间分布。

2 GPS高程拟合

2.1 GPS高程拟合原理[2]

GPS测量得到的是地面点相对于WGS-84椭球面的大地高(H)，而我国的实用高程采用的是相对于似大地水准面的正常高(h)，大地高与正常高的差值为高程异常(ζ)[2]。它们的关系为：

ζ=H-h

(1)

高程异常是高程拟合的关键，求得高程异常，就可以根据该高程异常应用式(1)求得测点的正常高。

2.2 GPS高程拟合方法

高程拟合法是在GPS网中联测一些分布均匀、密度适宜的水准点，根据这些水准点上的正常高和大地高拟合求出它们的差值，差值也就是高程异常值，然后根据这些点上的高程异常值与坐标的关系，用最小二乘法拟合出测区的似大地水准面，最后利用拟合的似大地水准面内插出其他GPS点的高程异常值[4]，利用式(1)求出各未知点的正常高。多项式拟合模型[5]：

设测区内任一点A(x，y)的高程异常ζ与平面坐标有如下的关系：

ζ=f(x，y)+ε

(2)

式中：f(x，y)为高程异常ζ的趋势面，ε为残差。设：

f(x，y)=a0+a1x+a2y+a3xy+a4x2+a5y2+a6x2y+a7y2x+a8x3+a9y3+……

(3)

若有n个点，则可以得到下面的矩阵形式：

ζ=AX+ε

在最小二乘的准则下，求得向量X的解，回带到式(3)中，就可以内插出未知点的高程异常[9]。再根据式(1)就可以算出GPS点的正常高。

在式(3)中，如果取未知数前三项，则称平面拟合，取前四项，称为四参曲面拟合，取前六项，称六参曲面拟合，以此类推[9]。曲面拟合就是采用一个数学曲面，来近似代替似大地水准面[9]。

2.3 精度评定

(1)内符合精度

内符合精度是由拟合点的拟合高程异常均值与分别拟合的高程异常值之差计算出来的[7]，即拟合残差按式(4)可计算出GPS水准拟合计算的μ：

(4)

(2)外符合精度

外符合精度是由检核点的高程异常与拟合高程异常之间的拟合残差按式(5)计算出来的[7]：

(5)

3 算例

根据具体工程项目详细地说明如何拟合区域似大地水准面。在某矿区建立一个控制面积仅 20 km2的GPS控制网，共23个控制点，南北长度约 5 km，东西长度约 4 km，网形如图1所示。每个GPS控制点都用S1级水准仪联测了四等水准，每公里水准测量精度是 9 mm，全网高程中误差最大 8 mm，平均高程中误差是 6 mm。根据高程异常拟合计算理论与方法，用Matlab编写了平面拟合、四参数平面拟合、六参数平面拟合程序，高程拟合的已知点是从23个控制点中选15个点，剩下的所有点是检核点，通过大量试算得到了理想的结果。已知点与拟合点的拟合高程异常，拟合残差结果及精度评定如表1所示。

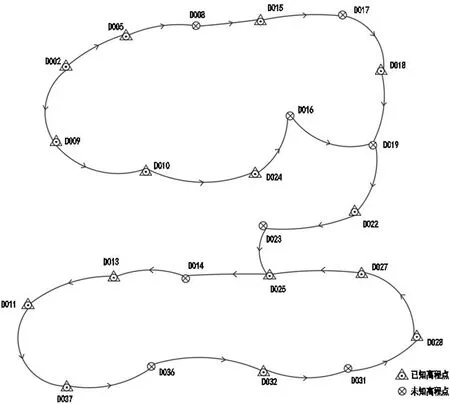
图1 本工程控制网图

表1 GPS高程测量与水准测量各种拟合结果及拟合残差

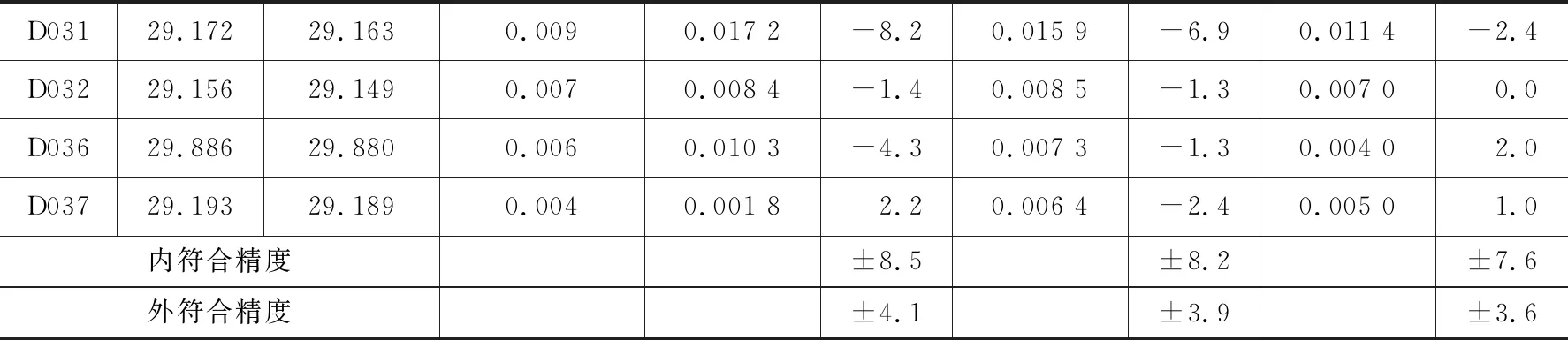
续表1

可以看出，平面拟合点最大残差为 -15.9 mm，四参数拟合点最大残差为 -14.8 mm，六参数拟合点最大残差为 -10.7 mm，六参数拟合结果最好，可达到三等水准测量的精度要求；四参数拟合结果也能达到四等水准测量的精度要求；平面拟合结果达到四等水准测量的精度要求。由此可见拟合结果可以用于工程实践。

4 结 论

(1)应当选择适当数量的水准联测点。如果选择太多联测点，会增加工作量；选择太少精度又得不到保证。水准重合点的数量在一个控制网中的要有10个左右已知点，最少6个。选择的水准重合点应尽量包含整个测区，且尽量分布均匀。按此法进行的GPS高程拟合其精度达到四等水准的要求，甚至三等水准要求，具有可靠性，能够满足工程需要。

(2)在工程实践中，在地形较为平坦且面积不大的地区可以使用“平面拟合法”进行高程拟合，对于地形较为复杂的地区，应该采用分区拟合法，并且增加水准联测点的个数，使拟合模型与拟合区域高程异常的变化更加接近。一般情况下如果点位分布均匀并且拟合的面积越小，得到的精度越高。

(3)利用GPS测量高程的方法可以确定地面点的高程和坐标，方便计算。而水准测量受人为影响很大，工作量大，消耗大量的人力、物力，GPS则操作简单，使工作效率得到提高。