基于Spearman-CS-ELM 的油气管道腐蚀预测模型

李世强 杨国栋 金龙 马宁 郄晓敏 王春洁

1中国石油华北油田公司第四采油厂

2河北华北石油工程建设有限公司

3华北油田公司储气库管理处

4中国石油华北油田公司二连分公司

在役管道受多种腐蚀因素的影响，其中外部腐蚀是管道失效的主要因素，管道一旦发生泄漏，会对生产、生活及周边环境造成不可弥补的损失[1-3]。因此，准确预测油气管道腐蚀深度，开展管道失效风险的评估，并有针对性地实施管道维修维护，对控制失效事故发生具有重要意义。

目前，研究人员针对腐蚀预测进行了大量研究。骆正山等采用广义回归神经网络（GRNN）对管道外腐蚀速率进行研究，但GRNN 模型在多维输入的情况下，网络训练时间会呈指数增长[4]；印翔等通过PSO 算法对传统GM（1，1）模型的背景权值进行智能寻优，构建了等维更新动态灰色模型，但灰色组合模型仅从时间序列上考虑了腐蚀发展的趋势，未涉及相关腐蚀因素的影响[5]；陈翀等提出了AIGA-WLSSVM 组合模型，但WLSSVM 模型的残差变量需满足正态高斯分布才可获得不错的预测精度[6]。本文应用斯皮尔曼（Spearman）相关系数进行腐蚀因素相关性的判别，利用因子分析进行降维处理，并引入极限学习机（ELM）对腐蚀速率进行回归，建立了一种新的腐蚀速率预测方法。利用该方法对某埋地管道腐蚀速率进行预测，预测值与实际检测值平均相对误差为2.32%。

1 基础模型

1.1 Spearman 相关系数

管道外腐蚀受土壤电阻率、含水量、含盐量、电位梯度、氧化还原电位等诸多因素的影响，根据数据特点，无法利用皮尔逊相关系数进行分析，故采用Spearman 相关系数判定腐蚀因素相关性，同时相关性分析也是进行因子分析的必要条件。Spearman 相关系数用于解决名称数据和顺序数据相关的问题，将两列变量排序后得到的成对位置称为秩次[7-8]，通过对比两变量秩次大小得到相关系数，相关系数越大，两变量的相关性越大，公式如下：

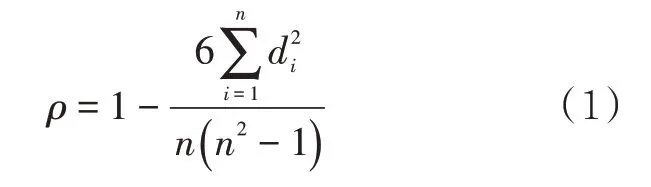
式中：ρ为Spearman 相关系数；d为秩次差值；n为样本数量。

1.2 基于CS 的ELM 模型

ELM 是一种针对单隐含层前馈神经网络的新型快速学习方法，可随机产生隐含层阈值和输入权值，相较于其余传统智能算法，具有迭代速度快、超参数少、泛化能力强等优点，只需确定隐含层节点数，即可获得唯一解，模型公式如下：

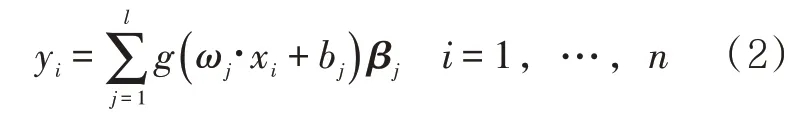
式中：yi为输出参数；g为激活函数；ωj为输入权值矩阵；xi为输入参数；bj为第j个隐含层阈值；βj为输出权值矩阵；1 为隐含层节点数。

在参数ωj和bj确定后，隐含层的输出矩阵H有唯一解，则输出权值矩阵βj可表示为：

式中：H+为矩阵H的摩尔-彭罗斯广义逆矩阵。

此时只需通过训练模型得到最优的βj，即可使输出参数yi的误差最小。但面临隐含层阈值和输入权值的随机选取，为防止ELM 模型陷入局部最优，将布谷鸟算法（CS）融入ELM 算法，利用CS 的寻优能力，寻找ELM 中超参数ωj和bj的最优解，以提高ELM 模型的预测精度。

CS 算法包括初始化种群、Levy 飞行搜索、淘汰最劣解、更新最优解等几个步骤，最终输出符合布谷鸟要求的优化目标鸟巢。MING 等通过对CS 算法在Sphere、Rosenbrock、Ackley 和Griewank 等四个通用测试函数上验证，证明了其在全局范围内寻优效果的优势[9]。Levy 飞行搜索包括随机游动和偏好游动的搜索方式，分别代表局部寻优和全局寻优，其位置更新公式如下：

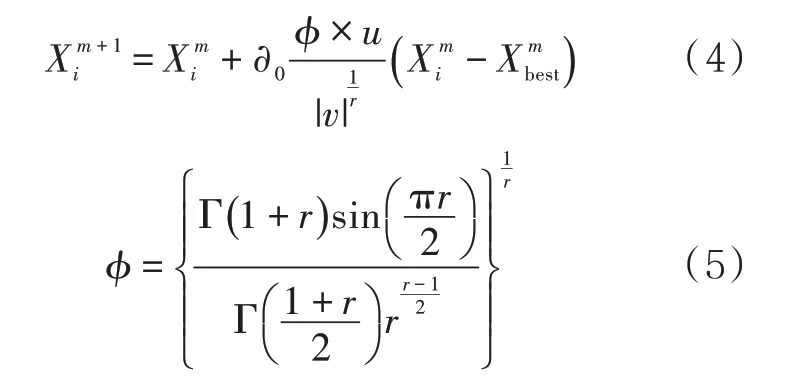
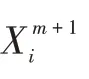
2 Spearman-CS-ELM腐蚀预测模型

当外腐蚀因素间相关性较强时，容易出现冗余信息，导致回归效果不佳。因此，当相关性较弱时，无需进行降维处理；当相关性较强时，可以通过R 型因子分析进行降维，得到重构后的样本集，以降低后期数据回归的复杂性；最后，将重构样本输入ELM 模型进行数据回归，并采用CS 算法对ELM 模型中的超参数进行寻优，获得最优模型。模型流程如图1 所示，具体步骤如下：

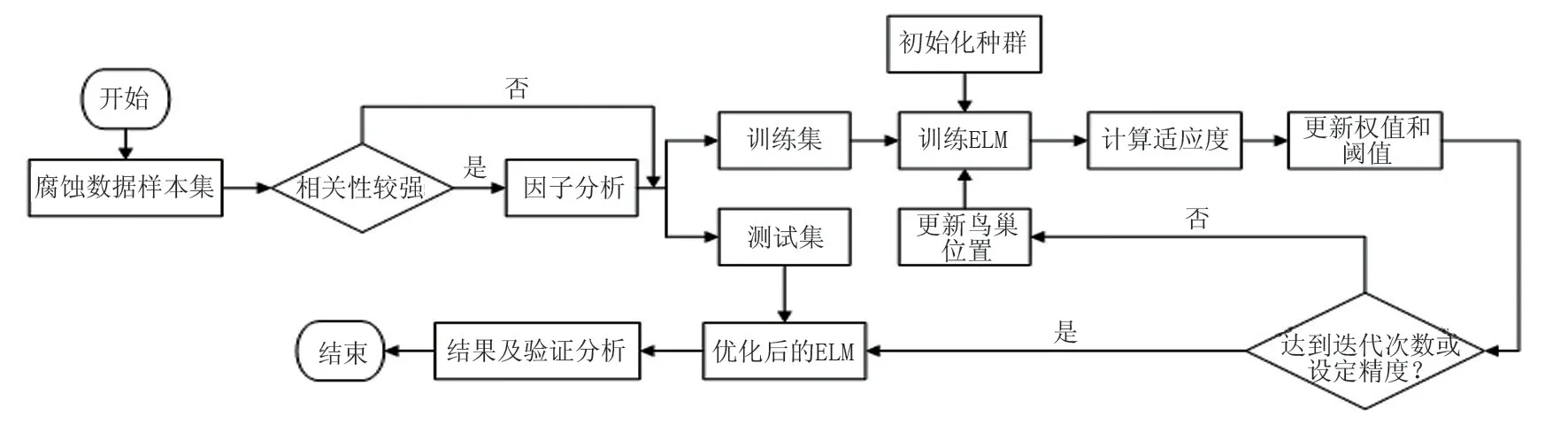
图1 腐蚀预测模型流程Fig.1 Corrosion prediction model flow

（1）相关性分析。通过实地埋片实验进行数据收集，计算各腐蚀影响因素之间的相关性，绘制Spearman 相关系数热度图。

（2）数据预处理。对数据进行标准化处理，并将样本集分为训练集和测试集。

（3）ELM 模型参数确定。ELM 模型中输入和输出层的节点数可根据样本集维数确定，初步确定隐含层节点数的范围为[2k+1，n]（k为输入层节点个数，n为样本个数），通过试算法确定隐含层节点数及激活函数。

（4）初始化CS 算法参数。以均方根误差(RMSE)为适应度函数，计算种群在迭代后的个体适应度值，评价个体优劣，通过CS 算法得到最优ELM 模型。

（5）预测分析。将测试样本输入最优ELM 模型中，得到预测结果，并通过评价指标对模型性能进行分析。

3 结果与讨论

3.1 实例背景

以某输气管道为例，该管道地跨2 省4 市，全长672 km，采用X65 管线钢，管径1 016 mm，壁厚10～12 mm，设计压力8 MPa，设计输量12×108m3/a，管道埋深1.2～1.5 m，管线采用3PE 防腐层加强制电流阴极保护联合方式防止外腐蚀。管道输送介质为净化天然气，CO2、H2S 含量均不超标，内腐蚀较轻，但在对管道防腐层进行ACVG、DCVG 外检测的过程中发现了不同程度的外壁腐蚀。

3.2 数据准备

通过资料收集与整理，按腐蚀原理将影响因素分为土壤性质、杂散电流、阴极保护和防腐层作用等四类，最终确定土壤电阻率μ1、pH 值μ2、含盐量μ3、Cl-含量μ4、SO42-含量μ5、含水量μ6、电位梯度μ7、阴极保护度μ8、破损点密度μ9等9个腐蚀因素[10]。沿程埋设同材质试片，通过定期观察试片外观并进行土壤采集获取所需数据，腐蚀速率采用失重法计算。在沿程选取具有代表性的30组腐蚀数据，其中1-24 组作为训练样本集，25-30组作为测试样本集，部分腐蚀数据见表1。

表1 埋地管道腐蚀数据Tab.1 Corrosion data of buried pipelines

3.3 数据预处理

计算各变量之间的Spearman 相关系数，结果如图2 所示。各腐蚀因素之间存在较强的相关性，为保持变量的独立性，避免相关性较大的因素对数据回归产生影响，对归一化后的数据进行因子分析，计算各变量间协方差矩阵的特征值和特征向量，并计算各成分的累积贡献率，结果如图3 所示。前6 个主成分的累积贡献占比为86.53%，累积贡献率超过了85%，说明前6 个主成分包含了原始变量的大部分主要信息。图4 为前6 个主成分相对原始变量的表达式系数绝对值，其中第一主成分中包含了阴极保护和防腐层保护分量的主要信息；第二、第三、第四、第六主成分中包含了土壤性质分量的主要信息；第五主成分中包含了杂散电流分量的主要信息。因此，提取后的主成分中包含了原始样本的丰富信息，优化了ELM 模型的输入变量。

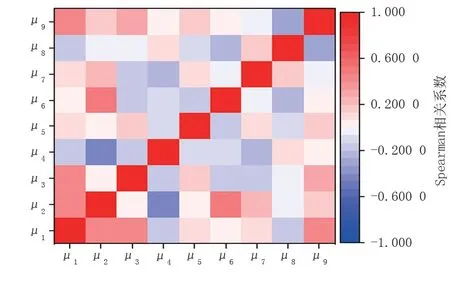
图2 Spearman 相关系数热度图Fig.2 Spearman correlation coefficient heat map

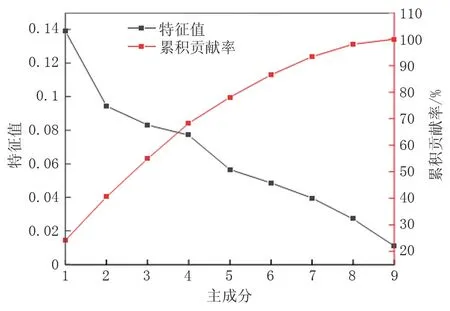
图3 样本特征值与贡献率计算结果Fig.3 Calculation results of sample eigenvalue and contribution rate

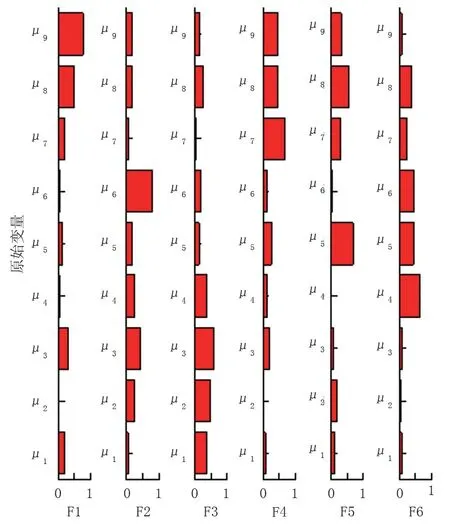
图4 主成分系数Fig.4 Principal component coefficient

3.4 模型参数确定

经因子分析降维后，确定ELM 模型的输入层节点数为6，输出层节点数为1，隐含层节点数为[13，30]。通过试算选择RMSE 最小的隐含层节点数及激活函数，其中常用的隐含层非线性激活函数有Sigmoid、Tanh、ReLU，最终预测结果如图5所示。

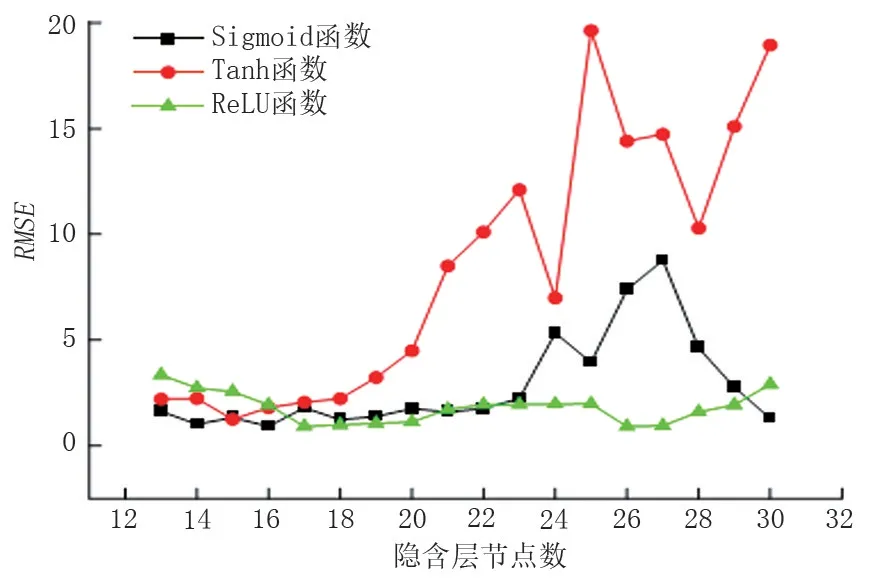
图5 不同隐含层节点数及激活函数的预测误差Fig.5 Prediction error of node number and activation function in different hidden layers

从图5 可知，三种函数分别在隐含层节点[13，22]、[13，19]、[17，20]之间的预测误差较小且较稳定，Sigmoid 函数和ReLU 函数分别有88.8%和44.4%的误差在6 以下；Tanh 函数的最大误差达到了19.65。其中ReLU 函数在隐含层节点数为17时，RMSE 最小为0.910 4，因此确定ELM 模型的激活函数为ReLU，隐含层节点数为17。此时CS 算法的迭代过程见图6，并采用粒子群算法（PSO）进行对比，CS 算法中种群规模取20，寄存蛋被发现的概率取0.25，搜索步长取0.6，Levy 飞行搜索系数取1.5；PSO 算法中种群规模取20，惯性权重取[0.8，1.2]，学习因子均取2，两种算法的迭代次数均为100。从图5 可以看出，PSO 算法和CS 算法分别在67、31 次迭代时趋于收敛，可见PSO 算法在迭代速度和寻优精度上均不及CS 算法。

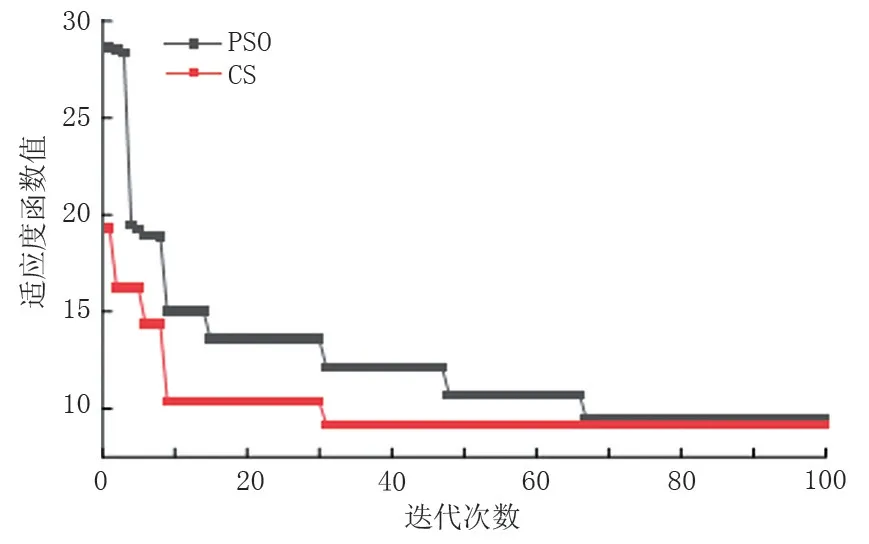
图6 不同寻优算法的迭代情况Fig.6 Iteration of different optimization algorithms

3.5 预测结果

为评价组合模型的预测效果，将测试集输入训练好的BP、PSO-GRNN 和Spearman-CS-ELM 模型进行对比，预测结果见表2。BP、PSO-GRNN 和Spearman-CS-ELM 模型在6 组测试集中的最大相对误差分别为20.25%、11.85%和5.03%，最小相对误差分别为2.54%、2.15%和0.50%，Spearman-CSELM 模型的最大最小误差均明显小于其余两种模型，且每组测试数据的相对误差均小于其余两种模型。

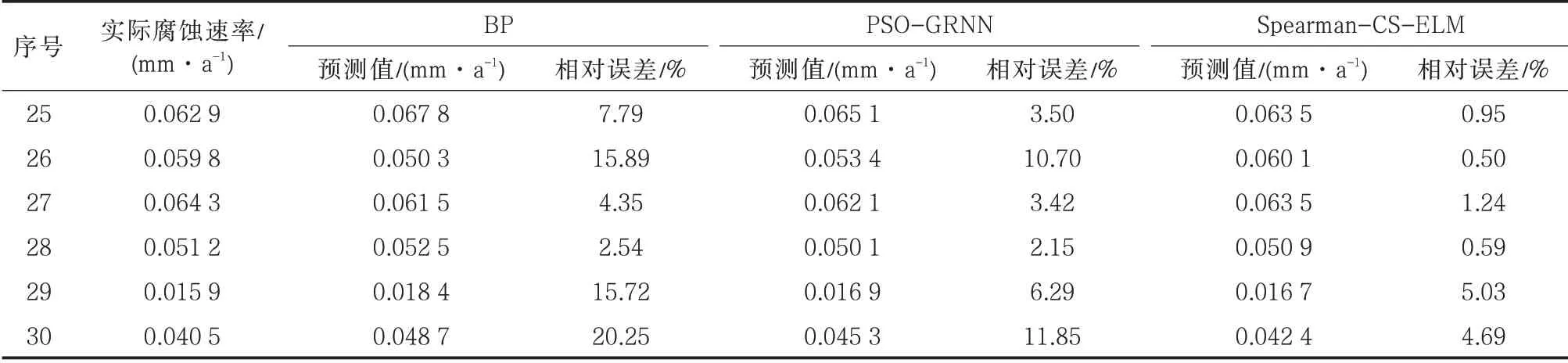
表2 不同模型预测结果对比Tab.2 Comparison of prediction results of different models

再次采用平均绝对误差（MAE）、平均绝对百分比误差（MAPE）和希尔不等系数（Theil IC）等3 个统计学指标，用于评价模型效果，结果见图7。Spearman-CS-ELM 模型的MAE、MAPE、Theil IC 最低，分别为0.000 783、2.168 和0.235，较BP模型减少了83.94%、74.72%、96.92%，较PSOGRNN 减少了73.46%、65.69%、89.05%，说明该模型的预测精度更高。

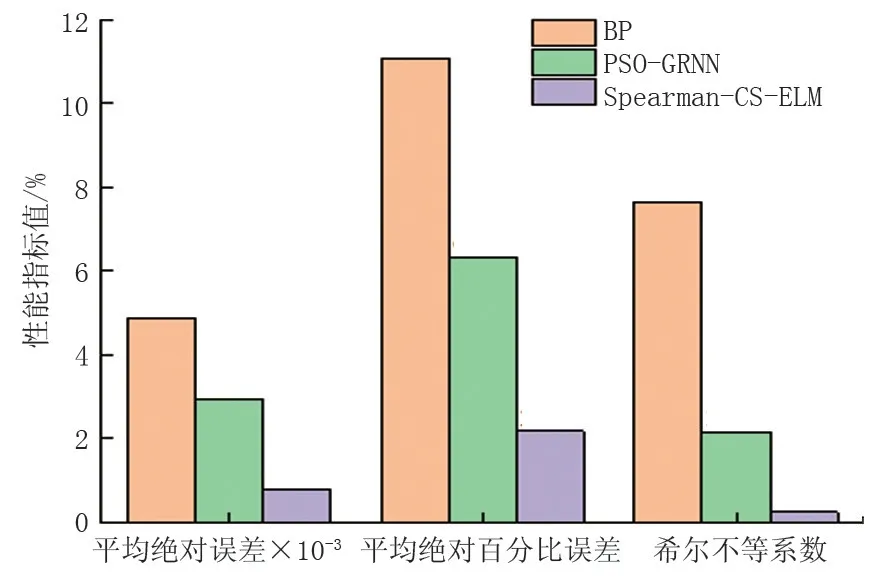
图7 不同模型性能指标对比Fig.7 Comparison of performance indicators of different models

3.6 模型有效性验证

为进一步考核模型的实际应用情况，选取了中国石油华北油田公司第一采油厂马二站—马一站集油线、文120 站—文118 站集油线、文118 站—文31 站集油线、文31 站—任三联集油线、任17 计—任一联油水处理站集油线等5 条具有典型代表性的管道进行腐蚀速率预测，并与现场实际值进行对比，结果见表3。可见预测值与实际值的平均相对误差仅为2.32%，满足实际生产中相对误差不超过5%的标准，说明该模型的适应性较好，可以用于指导现场实际生产，确定在役管道的剩余寿命和维修周期。

表3 现场应用效果Tab.3 Field application effect

4 结论

采用Spearman 相关系数判定各腐蚀因素之间的相关性，并采用因子分析对原数据进行降维处理，提高后续模型的计算速度；在ELM 模型的基础上，采用CS 算法对输入权值和隐含层阈值进行迭代寻优，并对不同的激活函数进行了对比，最终确定了隐含层节点数和激活函数；Spearman-CSELM 模型与其余模型相比，MAE、MAPE 和Theil IC 最低，模型的预测精度、泛化能力和稳定性最好，可用于埋地管道外腐蚀速率的预测。