简版数学焦虑量表在中国小学儿童群体中的修订及信效度检验 *

李红霞 徐艳丽 方怡泉 郭凯玥 司继伟

(山东师范大学心理学院，济南 250358)

1 引言

数学焦虑指个体在加工数字、使用数学概念、学习数学知识、解决数学问题或参加数学考试时所产生的不安、紧张、畏惧等反应（耿柳娜,陈英和, 2005）。它不仅影响个体的学业表现，还会损害身心健康（Jamieson et al., 2021），影响决策、职业选择与社会适应（Reyna et al., 2009）。近年来，数学焦虑已成为学术界乃至国际社会广泛关注的一个主题。

研究显示，数学焦虑在小学甚至在一二年级时就已经出现（Li et al., 2021; Tomasetto et al.,2021）。2018年，我国教育部基础教育质量监测中心在全国31个省（自治区、直辖市）和新疆生产建设兵团抽取了331个样本县（市、区）的4141所小学，对116 631名四年级学生的数学焦虑进行评估，结果显示24.8%的四年级学生报告中等及以上水平的数学焦虑。由此可见，如何全面准确地考察小学儿童数学焦虑成为当务之急。尽管关于数学焦虑的研究已取得很大进展，但从研究对象来看，大部分研究是在西方、受过教育、工业化、富裕和民主社会（western, educated, industrialized, rich, and democratic, WIRED）的群体中进行的（Henrich et al., 2010），并且关注的对象主要为青少年（Geary et al., 2021; Xie et al., 2019）与成人（Jamieson et al., 2021），对中国学生尤其是小学儿童数学焦虑的研究相对不足，原因之一可能是缺乏有效的测量工具。

回顾近十几年国内外该领域研究，当前儿童数学焦虑量表主要有以下几个特点。

第一，从项目内容与长度来看，儿童数学焦虑量表多是在成人量表基础上进行修订，并缩减其项目数。以目前国外使用最广泛的量表之一简版数学焦虑量表（the Abbreviated Math Anxiety Scale, AMAS）为例，其原始量表是基于大学生被试开发的，包含9个项目（Hopko et al., 2003），现已被翻译成多国语言版本，广泛用于评估儿童数学焦虑。我国学者也曾用AMAS考察儿童数学焦虑，但仅对量表进行了翻译，并未修订，有些项目不适用于小学尤其是低年级儿童，例如“看老师在黑板上写代数方程式”（王梦媛, 2018）；于海媚等人（2021）对该量表进行了修订，发现AMAS在中国初中生群体中信效度良好。至于在小学儿童中，AMAS有待进一步修订和完善。

第二，从量表结构来看，儿童数学焦虑表现出多个维度。以往研究普遍认为数学焦虑存在多种结构（Hopko et al., 2003）。但这些研究结果大都是在青少年和成人群体研究中获得的，儿童数学焦虑是否也存在多种结构呢？H a r a r i等人（2013）在一年级儿童报告的数学焦虑中区分出了消极反应与担心维度；使用AMAS在成人中发现了数学评估焦虑与学习数学焦虑维度，修订后的AMAS在儿童中同样发现了上述两种维度（Carey et al., 2017）；我国学者修订的儿童数学焦虑量表（Mathematics Anxiety Scale for Children, MASC）也在小学儿童中发现了数学评估焦虑、学习数学焦虑的不同维度（耿柳娜, 陈英和, 2005）。这些结果均表明，数学焦虑在小学儿童阶段就是多维的结构，这些结构可能会映射到青少年和成人身上。

第三，从项目反应方式来看，当前量表主要采用言语、具有不同等级梯度的表情图片或者两者的结合进行计分。使用言语计分的量表如儿童数学焦虑量表（MASC）采用4点计分（耿柳娜,陈英和, 2005）。对于小学低年级儿童来说，等级梯度表情图片（即通过面部表情把不同水平的数学焦虑直观地表示出来）这种反应形式更易于理解。如儿童数学焦虑问卷（Child Math Anxiety Questionnaire, CMAQ）的评估对象为小学1～2年级儿童，该量表要求儿童用一个滑动的16点标尺来回答每个项目，每个项目包含从“紧张”到“平静”三种表情（Ramirez et al., 2013）。但该量表是单维结构，无法对儿童数学焦虑的不同维度进行考察。

本研究在量表修订中，对上述优点进行了借鉴。同时，本研究也发现了现有儿童数学焦虑量表的一些局限。首先，项目反应方式主要为Likert计分（如儿童数学焦虑量表MASC）。研究发现，低龄儿童不能很好地从心理上表征数字本身与它所代表的意义（Deloache, 2000; Holmes & Lourenco,2011），也就是说，低龄儿童在将数字“4”与情绪“非常焦虑”联系起来时存在困难。传统的Likert计分方式（从“不同意”到“非常同意”）对小学儿童尤其是低年级儿童而言是不适用的。其次，样本量较小，没有对量表在不同群体（如年级和地区）中的测量等值性进行检验。除Jameson（2013）编制的儿童数学焦虑量表涵盖了小学1～5年级以外，其他量表仅涉及某一个年级、小学低年级或者小学高年级（Harari et al., 2013），这些量表是否适用于其他年级？此外，在青少年与成人群体中，数学焦虑存在性别差异（Ganley &Vasilyeva, 2014; Xie et al., 2019），但是儿童数学焦虑的性别差异尚不明确。换言之，儿童数学焦虑在不断发展变化，有必要修订或开发一个跨年级、性别测量等值的量表以考察小学1～6年级儿童数学焦虑的发展变化情况。另外，已有关于数学焦虑的研究绝大部分关注的是“WIRED”文化下的群体，对中低收入地区儿童的研究还有待加强。

本研究的主要研究目标是：（1）对AMAS进行修订，开发一个适用于我国儿童的数学焦虑量表，即中文版简版数学焦虑量表（the Chinese version of Abbreviated Math Anxiety Scale, AMASC），并检验信效度；（2）使用多组验证性因素分析考察AMAS-C在不同性别、年级与地区（城市、县城）的测量等值性，使新量表适用于1～6年级城市与县城儿童。

2 研究方法

基于以往研究，在修订儿童数学焦虑量表时，遵循以下几条标准：（1）修订量表必须得到原始量表开发者的知情同意；（2）量表项目来自于信效度较高的适用于年龄较大群体的量表；（3）项目必须符合儿童的认知发展阶段，项目内容为儿童可以接触到的问题或情景、包含多个维度，项目反应方式采用言语与表情梯度图相结合的方式、使用简单的句子结构和语言；（4）量表长度适中，适合进行团体施测。

2.1 量表的汉化过程

2.1.1 量表来源

通过与AMAS（Hopko et al., 2003）、CMAQR（Ramirez et al., 2016）原版研发者邮件沟通，获得本研究对原版AMAS量表进行修订以及使用CMAQ-R部分内容的许可。

2.1.2 翻译、回译与校正

本研究对简版儿童数学焦虑量表的修订过程包括以下三个步骤。（1）量表翻译。首先由2名熟悉本领域且英文较好的研究生将Hopko等人（2003）研发的AMAS量表翻译成中文。（2）量表校正。由团队中的2名博士对预测问卷进行表述纠错，避免项目出现歧义、冗长、难以理解等问题，然后经过与2位教龄超过7年的小学数学教师以及1位心理学专家充分讨论后，将超出小学阶段学习范围或不适用的部分内容进行替换，最终确定中文版量表。（3）量表回译。由英语专业的高校老师将中文版量表回译成英文，两版没有差异。

2.2 被试

样本1：采用目的抽样方法选取小学1～6年级学生35人（1～6年级分别为7人、7人、6人、5人、5人、5人）参加认知访谈，其中男生19人（54.29%）。

样本2：采用分层抽样的方法选取山东省某城市与县城三所小学1～6年级儿童被试共3140人，删除未认真作答（11人）与未完成测验（45人）被试共56人，最终有效被试3084人（年龄范围6～12岁，平均年龄8.85±1.31岁，男生1616人）。将被试随机分割成预测样本（n=967）和正式样本（n=2117）。预测样本用于量表的项目分析、探索性因素分析、信度分析和效度分析；正式样本用于量表的验证性因素分析和跨组分析（性别、年级与地区）。所有被试均由父母签署知情同意书，完成测验后每名被试获得一份小礼物作为报酬。预测样本被试详细信息见表1。

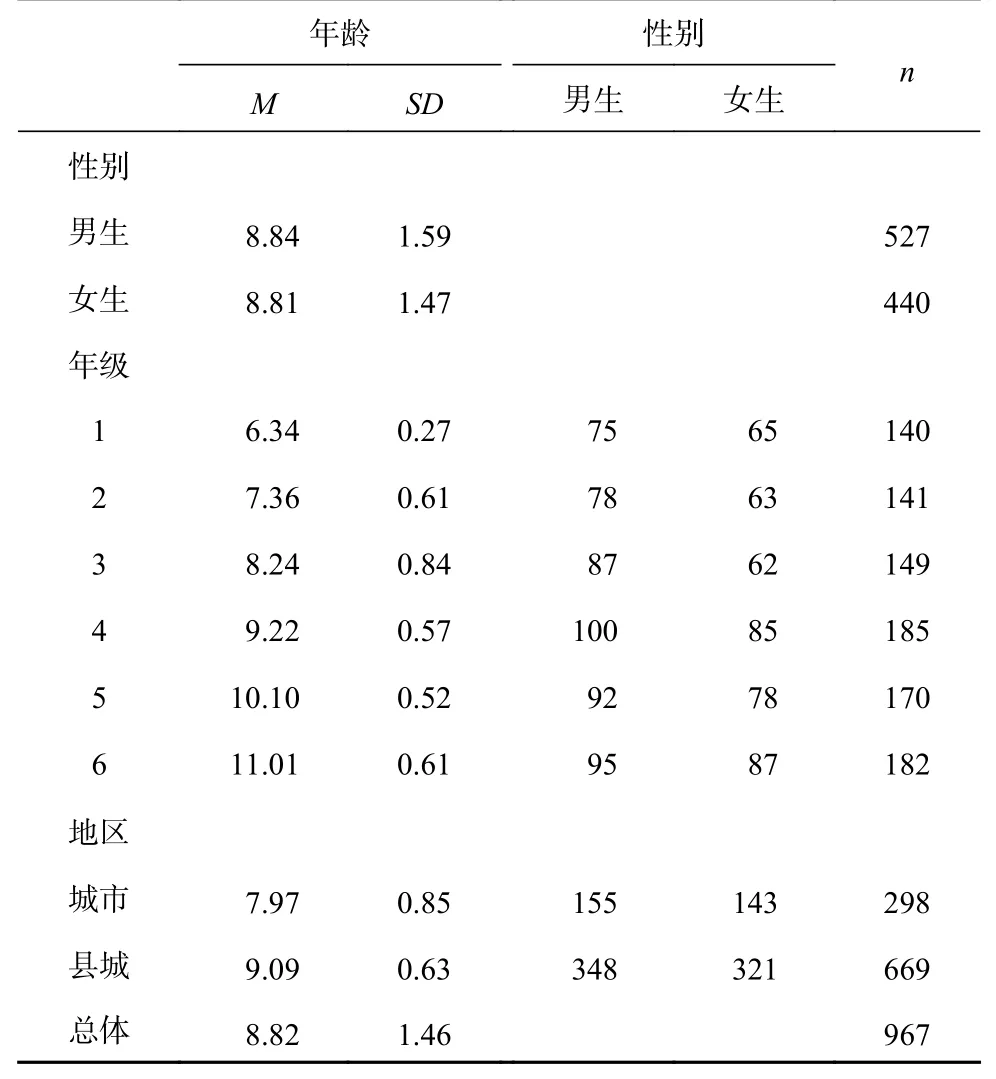
表 1 预测样本被试基本特征（n=967）

样本3：2周后，从样本2中随机选取298人进行重测，剔除无效数据后，获得272对匹配数据，其中男生154人（56.62%），该数据用于量表的重测信度分析。

2.3 研究工具

2.3.1 中文版简版儿童数学焦虑量表

中文版简版儿童数学焦虑量表共有9个项目，包含数学评估焦虑（math evaluation anxiety,MEA）与学习数学焦虑（learning math anxiety,LMA）两个维度。采用4点计分，1～4分别对应着4张不同情绪梯度的表情，表示从“没有焦虑”到“极度焦虑”。9个项目的平均分即为儿童的数学焦虑得分。原始量表具有较好的信度，总量表及两个分量表的Cronbach’s α系数大于0.74（Hopko et al., 2003）。

2.3.2 一般焦虑量表

采用Spence等人（2001）编制的学前儿童焦虑量表。量表共有29个项目，包括广泛性焦虑、躯体伤害恐惧、社交恐惧、强迫-冲动障碍和分离焦虑五个维度。采用5点计分，从0到4代表“从不焦虑”到“总是焦虑”。得分越高，焦虑程度越高。本研究选取该量表中的广泛性焦虑维度测量一般焦虑。该量表在我国儿童中具有良好的信效度（司继伟 等, 2022）。本研究中该量表的Cronbach’s α系数为0.91，信度良好。

2.3.3 考试焦虑量表

采用Sarason（1978）编制的考试焦虑量表，该量表包含37个项目，涉及测验情境中的生理、情感、认知和行为反应。要求被试根据自己的情况回答“是”或“否”，“是”计1分，“否”计0分，得分越高，表示考试焦虑程度越高。本研究中该量表的Cronbach’s α系数为0.86，信度良好。

2.3.4 儿童数学焦虑量表

采用耿柳娜和陈英和（2005）修订的儿童数学焦虑量表（MASC）。该量表共有22个项目，包括四个因素（数学评估焦虑、数学学习焦虑、数学问题解决焦虑和教师焦虑）。量表采用4点计分，从1到4代表“没有焦虑”到“极度焦虑”，得分越高，表示儿童数学焦虑水平越高。在本研究中，总量表及四个分量表的Cronbach’s α系数在0.87～0.92之间，信度良好。

2.4 施测程序

首先，对济南市和潍坊市县城某小学35名被试进行了一次认知访谈，时间大约为40分钟，每20分钟为一个阶段。在认知访谈中，要求被试完成中文版简版儿童数学焦虑量表。对于1～3年级的儿童，访谈时由研究者大声朗读每一个项目，要求被试回答，4～6年级儿童则是自己独立完成测试。测试结束后，研究者让被试解释每一个项目，以判断被试是否准确地理解每个项目的意思。

根据被试的反馈，本研究对量表进行了以下修订。（1）使用多个同义词描述焦虑。例如原始量表仅使用了“焦虑（anxiety）”，而与之相比，低年级儿童更容易理解“紧张（nervous）”，因此在量表中使用了“紧张或者焦虑”等字样。（2）参考Ramirez等人（2016）所使用的CMAQ-R，将AMAS的数字计分反应方式改成Smiley-face scale和数字相结合的反应方式。（3）由于学生对“中等焦虑”的理解不够准确，参照以往研究，将5点计分改成了4点计分，即去掉了“中等焦虑”（耿柳娜, 陈英和, 2005）。

然后进行集体施测。由经过严格培训的心理学研究生与本科生担任主试。施测前，主试向儿童解释“焦虑”的含义，并逐一解释每个表情图对应的焦虑程度。测验完成后问卷当场收回。

2.5 数据管理与分析

运用SPSS26.0和Mplus8.3进行数据整理和分析。本研究数据分析主要包括三部分：第一，对预测样本（n=967）进行两因素探索性因素分析。采用主轴因素法提取因子，假设潜在因子之间存在相关，因此使用斜交旋转（direct oblimin）。通过因子载荷、特征根、贡献率和碎石图判断数据拟合情况。计算AMAS-C与儿童数学焦虑量表（MASC）之间的相关，考察实证效度。然后计算AMAS-C与一般焦虑以及考试焦虑之间的相关，考察AMAS-C的区分效度。第二，对正式样本（n=2117）进行验证性因素分析，以确定前一阶段建立的因素结构是否充分。第三，运用Mplus 8.3建构一系列嵌套模型，使用验证性因素分析考察数学焦虑的多组（性别、年级与地区）测量等值性。分析步骤为：（1）形态等值，假设不同组之间，潜变量的构成形态或模式是相同的，如果形态等值模型接受，则应用约束模型进行进一步的检验；（2）单位等值或弱等值，假设因子负荷跨组不变；（3）尺度等值或强等值，假设观测变量的截距具有不变性。

3 结果

3.1 预测样本

3.1.1 项目分析

对全部条目进行项目分析。首先，该测验属于非能力测验，需要进行“通俗性”检验（即能力测验中的难度检验），各题目的难度介于0.36～0.61之间。其次，计算量表每个条目与总分、所在维度的相关系数，结果表明，相关系数均在0.51以上（ps＜0.001），并且每个条目与所在维度的相关系数均高于与总分的相关。最后，按总分对所有被试排序，分成高分组和低分组（即得分前、后27%），对数学焦虑高低分组进行独立样本t检验，9个条目上的t值均达到显著水平（ps＜0.001）。这表明量表各条目的难度、区分度、鉴别力良好。

3.1.2 探索性因素分析

对所有被试数据进行探索性因素分析，KMO值为0.85（p＞0.50），Bartlett’s球形检验结果显著[χ2(36)=1779.14,p＜0.001]，反映像相关矩阵的对角线数值全都大于0.5，满足进行探索性因素分析的前提条件。最佳因子解释通过碎石图（见图1）、因子解释率和因子特征根确定。两因素探索性因素分析的方差解释率为53.14%。数学评估焦虑因子载荷的范围是0.71～0.84，学习数学焦虑因子载荷范围是0.51～0.75（见表2）。

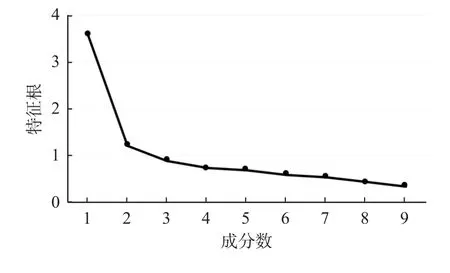
图 1 碎石图

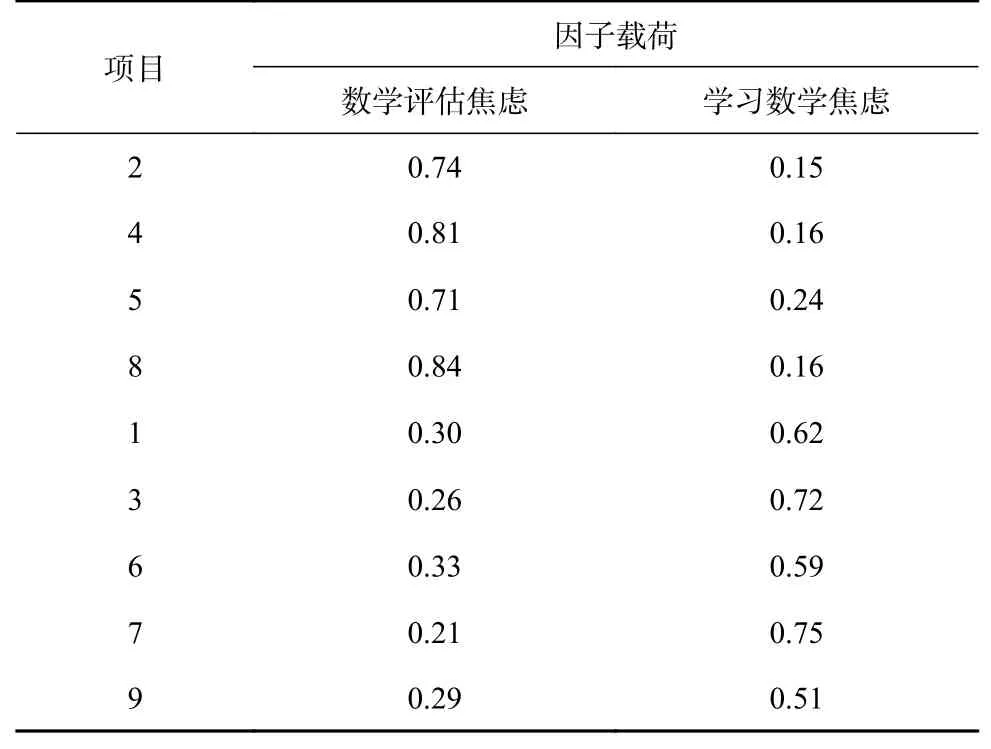
表 2 中文版简版儿童数学焦虑量表各项目的因子载荷（n=967）

3.1.3 描述性统计与信度检验

预测样本自我报告的数学焦虑的描述性统计结果如下：总量表（M=1.95,SD=0.78），数学评估焦虑（M=2.28,SD=1.07），学习数学焦虑（M=1.63,SD=0.67）。总量表及两个分量表（MEA与LMA）内部一致性系数分别为0.82、0.80、0.78，信度良好。

3.1.4 效度检验

AMAS-C总量表与各维度、各量表的相关结果见表3。结果显示，AMAS-C总分及各维度得分与MASC的相关在0.72～0.82之间，与一般焦虑与考试焦虑的相关在0.30～0.56之间，表明AMASC具有较好的效标关联效度和区分效度。

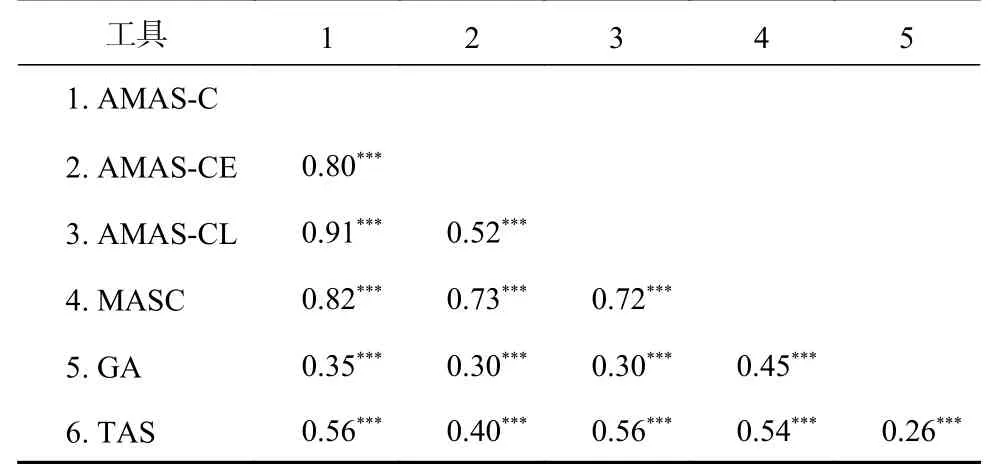
表 3 数学焦虑与其他变量相关矩阵（n=967）

3.2 正式样本

3.2.1 验证性因素分析

建构两因素验证性因素分析模型检验量表的效度。模型拟合指数良好（χ2/df=3.00,p＜0.05,RMSEA=0.04, CFI=0.98, TLI=0.98），表明该量表具有较好的结构效度。两维度数学焦虑因子载荷的范围为0.48～0.79（见图2）。

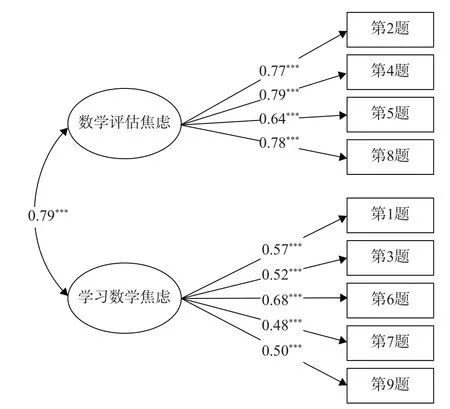
图 2 中文版简版儿童数学焦虑量表验证性因素分析

3.2.2 描述性统计与信度检验

正式样本自我报告的数学焦虑如下：总量表（M=1.96,SD=0.77）；数学评估焦虑（M=2.34,SD=1.07）；学习数学焦虑（M=1.59,SD=0.63）。总量表、数学评估焦虑与学习数学焦虑的Cranbach’s α系数分别为0.85、0.77、0.82。1～6年级被试总量表Cronbach’s α系数的范围为0.77～0.85。间隔两周后，AMAS-C的重测信度为0.70～0.79。

3.2.3 多组测量不变性检验

所修订AMAS-C量表的模型拟合指数结果见表4，形态等值模型（模型A）的各项拟合指数均比较理想，满足进行等值检验的条件。在限定男女两组因子负荷相等（模型B）中，各拟合指数与未限定相等的形态模型相比变化不大，卡方差异检验结果不显著[Δχ2(7)=1.67,p＞0.05]，证实了弱等值成立假设。进一步限定项目截距跨组等同即强等值（模型C），卡方差异检验不显著[Δχ2(7)=6.11,p＞0.05]，表明强等值假设成立。上述结果说明，AMAS-C两因素模型满足性别测量等值性，该量表项目在男女生之间具有相同的意义和功能。

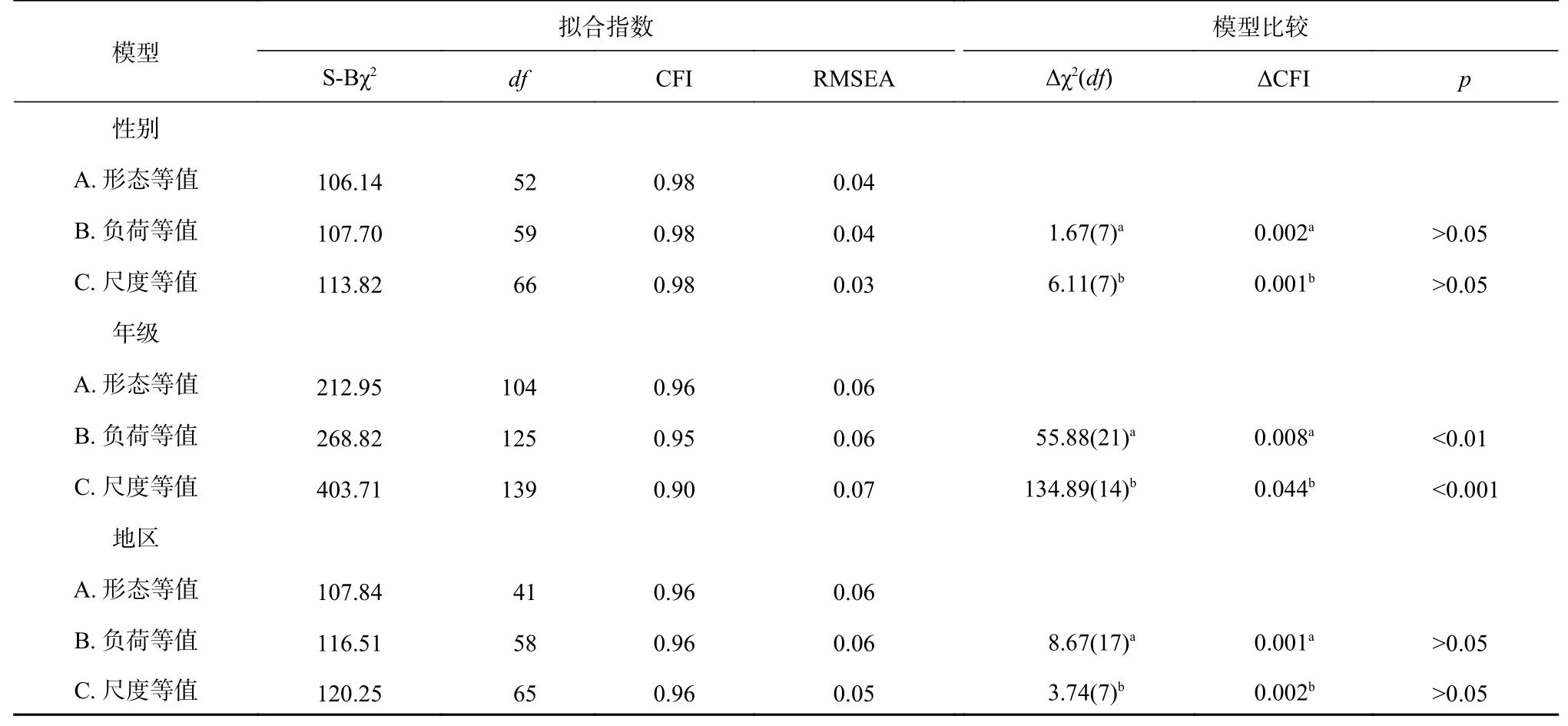
表 4 AMAS-C因子模型多组等值性拟合指数及模型比较结果（n=2117）

年级跨组比较结果（见表4）显示，在设定弱等值模型（模型B）中，卡方差异检验结果显著[Δχ2(21)=55.88,p＜0.01]，但是ΔCFI=0.008、ΔTLI=0.005，均小于0.01，说明弱等值成立（Meade et al.,2008）。进一步限定项目截距跨组等同即强等值（模型C），卡方差异检验显著[Δχ2(14)=134.89,p＜0.001]，且ΔCFI与ΔTLI均大于0.01，说明强等值不成立。这表明项目截距在不同年级被试中存在差异，也就是说不同年级数学焦虑水平存在差异，但是AMAS-C形态（数学焦虑的构成形态或模式）和项目因子负荷在不同年级等值，说明AMAS-C项目在不同年级之间具有相同的意义和功能。

地区跨组比较结果（见表4）与性别跨组比较结果一致，满足地区测量等值性，AMAS-C项目在城市与县城被试之间具有相同的意义和潜在结构。

4 讨论

尽管越来越多的证据表明，数学焦虑在小学低年级就已经出现，但由于缺少有效的测量工具，目前关于低年级儿童数学焦虑的研究还十分有限，尤其是在中国文化背景下。本研究采用大样本对AMAS进行汉化和修订，首次建立了适用于小学1～6年级儿童的中文版简版数学焦虑量表。并检验了AMAS-C的信度、效度，以及该量表的多组（性别、年级与地区）测量等值性。

4.1 AMAS-C的信度

研究结果显示，AMAS-C总量表的内部一致性信度很好，数学评估焦虑与学习数学焦虑两个分量表的内部一致性信度也较好，表明AMASC在我国小学儿童中也具有较高的信度。此外，本研究还分别计算了各个年级儿童数学焦虑的内部一致性信度，信度系数仍保持较高，表明在小学1～6年级各个年级，AMAS-C都是一个可靠的量表，这可能也是该量表优于其他量表的一个地方。比如小学中高年级数学考试焦虑问卷（秦燕琼, 2019）仅适用于小学3～6年级儿童。

4.2 AMAS-C的结构效度、效标关联效度与区分效度

AMAS包含数学评估焦虑与学习数学焦虑两个维度（Hopko et al., 2003）。本研究结果表明，两因素数学焦虑模型同样适用于中文版本。因子载荷的范围为0.48～0.79，均达到了可接受的范围。

本研究分析了AMAS-C与国内常用的具有良好效度的儿童数学焦虑量表（耿柳娜, 陈英和,2005）之间的相关，发现两个量表具有强相关，表明AMAS-C具有很好的实证效度。此外，AMASC与一般焦虑、考试焦虑量表的相关分别为0.35、0.56。尽管AMAS-C与两种焦虑有重叠，但AMAS-C与数学焦虑不同维度之间的相关性更强（0.80～0.91），这与Ashcraft（2002）观点基本一致，表明本研究所修订的AMAS-C区别于一般焦虑与考试焦虑，真正衡量了数学焦虑。该结果表明，即使是在小学儿童中，数学焦虑也是一个区别于其他焦虑类型的独立结构。

4.3 AMAS-C在不同性别、年级与地区的适用性

本研究的一个重要贡献是考察了AMAS-C在不同群组（性别、年级与地区）中是否具有相同的意义和潜在结构。

首先，AMAS-C满足性别测量等值。具体来说，以男女生两组数据所建构的模型在数学焦虑两个维度（潜变量）与对应的各项目（显变量）之间的基本结构关系对等，数学焦虑测量指标与因子之间的关系在各组间等值，观测变量之间的截距具有不变性。因此，AMAS-C具有跨性别等值性。如前文所述，国外研究发现与男生相比，女生报告了更多的焦虑情绪（Frenzel et al., 2007）。但也有研究者考察了数学焦虑不同维度的性别差异，发现男生的特质焦虑显著高于女生，而在状态焦虑上，虽然性别差异不显著，但是男生的得分略高于女生（Goetz et al., 2013）。本量表可以用于考察我国不同性别儿童数学焦虑的特征。

其次，本研究证明AMAS-C具有跨年级测量等值性，在不同年级样本中具有相同的潜在结构和意义。该量表可以用于评估小学1~6年级儿童数学焦虑的特征，考察小学儿童数学焦虑的发展变化与数学表现相关的因素。

最后，本研究比较了城市和县城两个群体，发现AMAS-C测量了相同的结构，确保该量表可以用来比较城市和县城小学儿童的数学焦虑。目前，国内已有研究分别考察了城市（崔吉芳 等,2011）、乡镇（张婕 等, 2018）学生的数学焦虑，但少有研究考察数学焦虑的地区差异，本研究所修订的量表为儿童数学焦虑的地区差异研究提供了有效的工具。

5 结论

中文版简版儿童数学焦虑量表具有良好的信效度，具有跨性别、年级和地区测量等值性，可作为测量我国小学儿童数学焦虑的有效工具。