基于FDTD-EMTR和地闪记录的闪络故障测距优化方法

李 轶，杨欢红，张 成，陆敏安，方 祺

（1.国网上海青浦供电公司，上海 201799；2.上海电力大学，上海 200090）

0 引言

近年来，随着系统电容电流增加，出于绝缘安全考虑，配电网系统小电阻接地改建比例大幅度上升，线路跳闸率大幅提升，外力破坏等引发的跳闸率也有所提升，对于配电网线路的运行安全性带来较大考验[1-4]。

通常线路的跳闸来自绝缘子或避雷器击穿闪络。对于35 kV 以下的架空线路，由于其绝缘子爬距较短，绝缘余量较小，雷击过电压造成的绝缘子闪络，或避雷器击穿闪络跳闸事故频率很高。尤其是电压等级较低的线路，300～400 kV 的感应雷过电压就足以造成其闪络故障。雷电定位系统能够有效监测雷电活动，精确记录雷击数据，多被应用于雷电密度统计研究。若能将测距装置与雷电定位相结合，提出有效的闪络故障测距优化方法，对于降低巡线难度、缩短恢复送电时间具有重要实际意义。

现阶段，研究人员对故障测距的结果优化仍从行波的角度进行深入探索。对于行波测距的优化又分为波头识别法[5-6]、分区定位[7-9]和多测距方式校正[10-11]。波头识别法的关键技术在于对行波性质的识别，但波阻抗不连续点的反射波时间值的标定受到电晕放电、波形振荡等因素影响，易误判造成误差；分区定位则是通过分析故障发生位置与过流报警器开关函数的对应关系，构建故障区段定位的数学模型，而弧垂、波速度等因素使得工程测距精度较低；多测距方式校正则是利用单端测距和双端测距相结合的方式进行故障距离校正，该方法对于测距装置在网络节点的放置要求较高。以计算故障行波的线路传播路程为基础的测距方法，未能充分考虑弧垂、杆塔跳线等实际工程问题对于行波传播距离的影响。

近年来，电磁时间反转（Electromagnetic Time Reversal，EMTR）被广泛应用于输电线路和电缆的故障定位中，通过仿真验证EMTR 在电力网络串联补偿线路和高压直流输电线路中均表现出较好的鲁棒性[12-14]。

文献[15-16]基于EMTR 理论提出了最大故障电流信号的故障点判断方法，无需增加额外设备且具有抗过渡电阻能力。文献[17]将其与遗传优化算法结合，在交流配电网实现了接地故障的有效测距，故障点的间距越小，故障定位精度越高。时域有限差分（Finite-difference Time-domain，FDTD）算法在雷击过电压的求解中取得理想效果，而FDTD算法在求解电报方程过程中能够获得线路任意一点的电压和电流，尽可能地缩短假设间距，提高故障定位的精度。

本文针对雷击造成的闪络故障，分别采用基于FDTD-EMTR 和地闪记录参考的方法提高闪络故障测距精度。通过FDTD 算法计算故障支路电流，以缩短EMTR 假设故障点间距；通过结合线路走廊趋势和地闪记录的相对位置和方向关系，建立接近度修正系数，以优化EMTR 测距结果，判断雷击杆塔点位置。通过国内某电网实测数据验证了方法的有效性。

1 故障测距理论

1.1 FDTD分析传输线瞬态响应

FDTD 算法在求解传输线电报方程时，可得到沿传输线任意点的电压和电流，而无损传输线的电报方程具有时间反转不变性，因此可将FDTD 算法与EMTR 理论相结合进行故障定位。

以单相单根无损导线为例，假设其单位长度的电容和电感分别表示为C和L，线路中的电压、电流是以线路上的位置z和时间t为变量的偏微分方程，则无损单导体传输线的电报方程为：

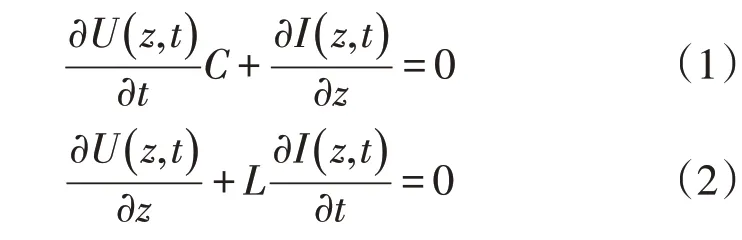
式中：U(z,t)为t时刻线路z处的电压；I(z,t)为t时刻线路z处的电流。

采用FDTD 对电报方程进行离散化。如式（3）—式（6）所示，采用中心差分法将式（1）和式（2）数离散化：

式中：Δz为被离散的空间步；Δt为被离散的时间步；NDZ为总仿真空间步；为nΔt时刻线路kΔz位置的电压；U为某时刻某位置上的电压；为nΔt时刻线路kΔz位置的电流；I为某时刻某位置上的电流。

考虑无损耗单导体传输线边界条件的方程为[18]：

式中：Rs，Rl分别为始端和末端位置电阻；Us,Ul分别为始端和末端位置电压；为nΔt时刻的末端电压；为nΔt时刻线路NDZ+1 位置的电压；为(n+1/2)Δt时刻线路NDZ位置的电流。

此外，为了保证FDTD 的准确性，时间步长和空间步长应满足Courant 稳定性条件，即：

式中：v为波速度。

图1 为单导体传输线故障电路FDTD 分析示意图。图1中，故障处的对地电压为Uf，故障点的接地电阻为为nΔt时刻线路kΔz位置的流入节点的电流，为nΔt时刻线路kΔz位置的流出节点的电流，为nΔt时刻线路(k-1) Δz位置的电压，为nΔt时刻线路(k+1) Δz位置的电压为nΔt时刻线路(k-1) Δz位置的电流，为nΔt时刻线路(k+1) Δz位置的电流，为nΔt时刻线路kΔz位置的故障电流。

图1 FDTD分析示意图Fig.1 Diagram of FDTD analysis

假设电流Iak流入节点，Ibk流出节点，根据FDTD 有如下方程：

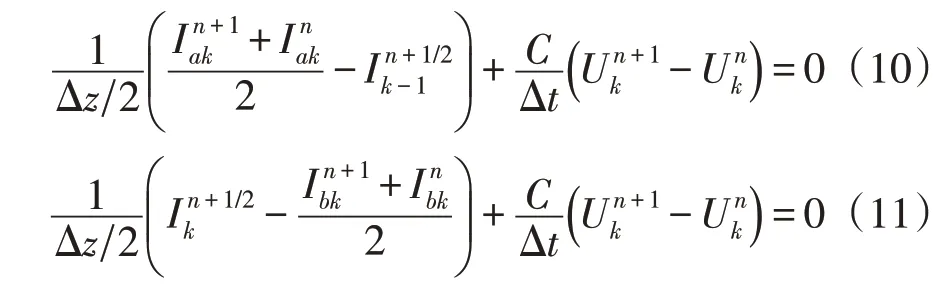
根据基尔霍夫定律，故障处的电压方程表达式可变换为：

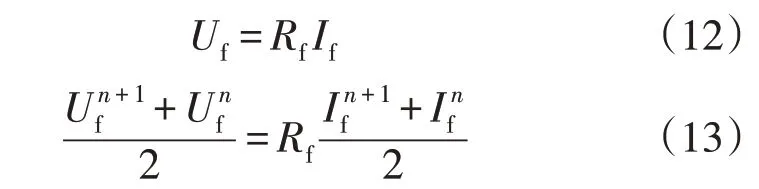
式中：If为故障电流。

故障处的电流方程表达式可变换为：

根据式（12）—式（15），故障处的节点电压方程可写作：

1.2 EMTR理论

电磁时间反转法通过所测信号注入回系统出现信号峰值的特点，实现对源位置和幅度的重构。式（17）为单导体无损传输线的电压波动方程表达式：

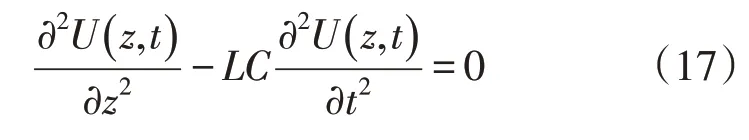
对其在时间轴取反，可以得到：

若U(z,t)为电压波动方程的解，那么U(z,-t)同样也是方程的解，即在时间反转变换下方程保持不变[19-20]。

根据EMTR 理论，对于设置的m个假设故障点（Guess Fault Locations，GFLs），反转信号从监测点反向注入回系统时，不同假设故障点的为：

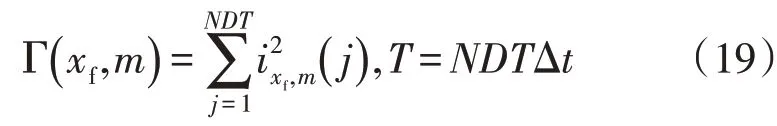
式中：xf，m为第m个假设故障点的故障距离；T为采样时间窗；NDT为总时间仿真步；ixf,m为nΔt时刻第m个假设故障点的电流值。

时间窗的目的是使电磁时间反转的自变量在信号的持续时间内为正，故添加一段时间延迟，本文中选取时间延迟为采样时间窗。

根据式（20）可知，能量最大值对应的位置为故障点的参考位置xf,real：

由于模型为无损镜像线路，考虑波速度的影响以及弧垂等不确定因素[21-22]会对闪络故障测距结果产生影响，需要对其进行一定程度的修正。

2 基于地闪记录的接近度修正系数测距结果优化

当雷击过电压或避雷器击穿等引起闪络故障时，雷电定位系统也会记录相应的地闪数据。由于线路走廊、波速度或环境因素的影响[23-24]，在实际工程应用中，会与测距结果产生一定偏差[25]，使得测距装置计算得到的故障点位置通常位于2 个杆塔之间。考虑到雷电定位系统可作为对闪络故障的不同视角刻画，可将雷电定位系统与测距装置进行数据融合达到偏差校正，实现测距结果的优化。

为更有效地利用参考故障点，需要对其进行归算处理。假设线路坐标表示为[(Lon1,Lat1,h1)，(Lon2,Lat2,h2)，…，(LonN,LatN,hN)]，其中，N为故障线路杆塔总数，Lon，Lat，h分别为杆塔的所在位置的经度，纬度与海拔。设线路杆塔的经纬度与海拔的坐标表示为(LonN,LatN,hN)，那么两杆塔间的距离dj,j+1为：

其中：

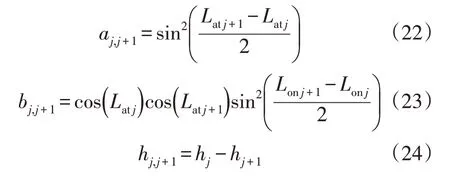
式中：j为杆塔标号；R为地球半径。

杆塔与监测装置之间的距离lj表达式为：

单次的地闪记录对于真实雷击位置的误差判断不能起到决定性作用。若对固定的线路杆塔位置坐标加权处理，可提高地闪位置判断的准确性。假设雷电定位系统监测到的雷击位置与其相对距离最短的杆塔编号记作TL，而1.2 小节EMTR 的测距结果得到的参考故障点所在杆塔编号记作TM。图2 为投影坐标图，建立最近邻地闪记录至电磁时间反转测距结果的空间位置向量ro，各基杆塔至电磁时间反转测距结果，即参考故障点的空间向量矩阵则表示为

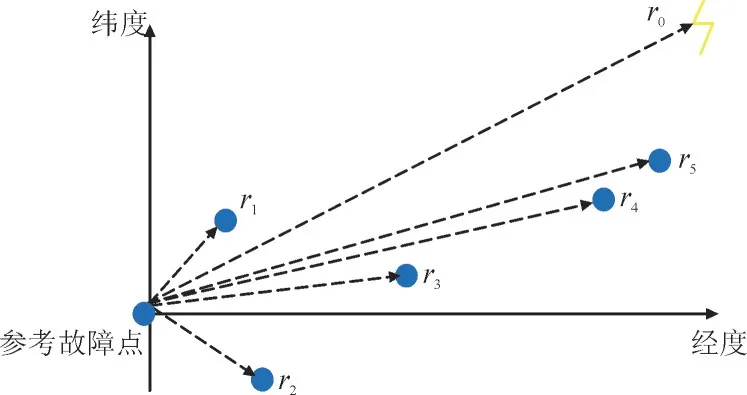
图2 投影坐标图Fig.2 Projection coordinate graph

r与ro之间的内积φ为：

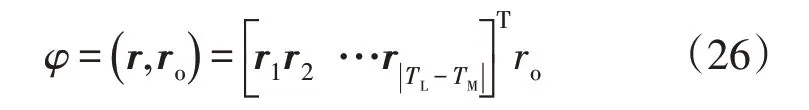
为了更好地表达杆塔与最近邻地闪记录对于电磁时间反转测距参考故障点的偏离程度，采用接近度判断雷击位置与杆塔相对于电磁时间反转测距参考故障点的方向。设各个基杆塔空间位置向量r与最近邻地闪记录位置向量的接近度p为：

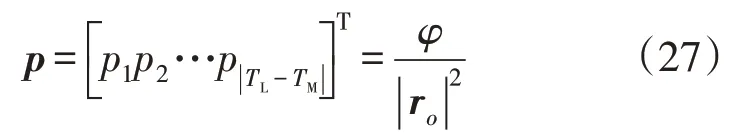
若pi＞0，则监测的雷击位置与杆塔相对于电磁时间反转测距参考故障点方向趋近一致，反之则方向不同；若pi=0，最近邻地闪记录与杆塔位置相重叠；若pi=2，最近邻地闪记录位于第i个杆塔与电磁时间反转测距结果间连线的某处。如式（28）所示，计算最大接近度pmax作为测距结果的修正系数：

则修正后的故障距离xop表达式如下：

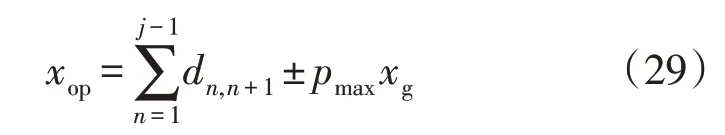
式中：xg为pmax所对应的杆塔到电磁时间反转测距参考故障的线路长度。

根据工程经验总结，配电线路在有绕击时耐雷水平比较大，同时装设双避雷线的情形下，发生雷电绕击线路的概率并不大，因此对于测距的误差影响在工程可接受范围之内。

3 闪络故障测距步骤

图3 描述了闪络故障测距流程，图3 中xf为故障位置。

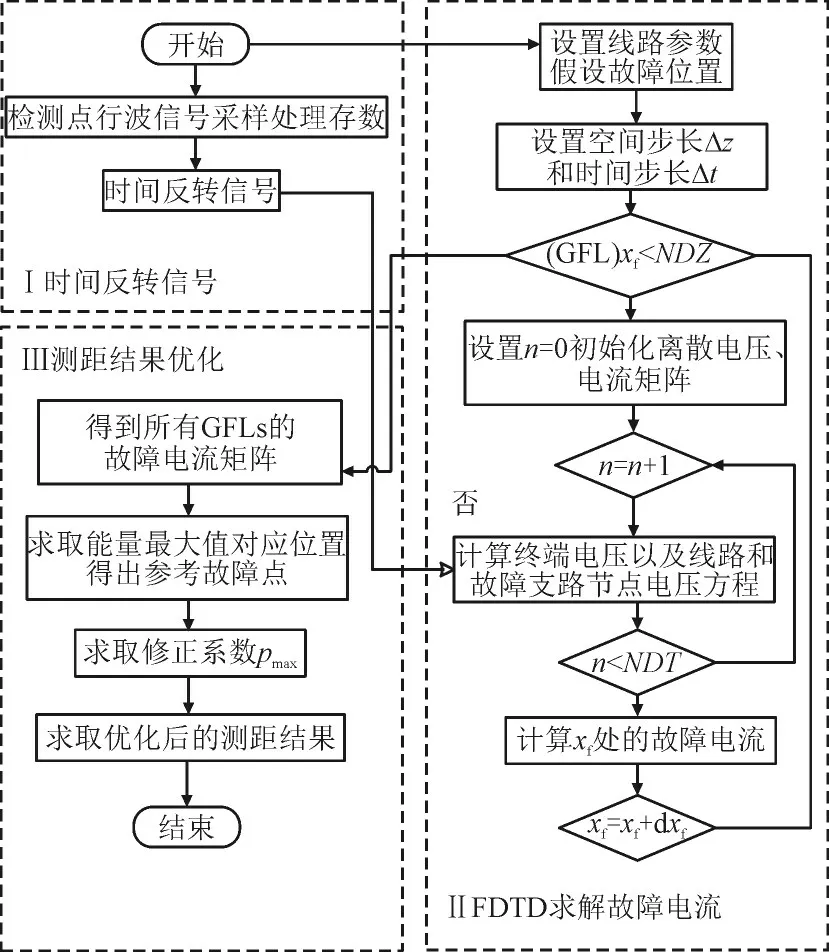
图3 闪络故障测距步骤Fig.3 Flow chart of flashover fault location

具体步骤如下：

步骤1：通过故障录波装置在检测点以预定采样频率对线路两端的故障行波暂态量进行采样和存数。

步骤2：将故障电流在时间窗内进行时间反转后作为系统的新电流源，并输入无损配电线路的特征参数为线路供电。

步骤3：通过FDTD 算法得出所有假设故障点的故障电流，计算故障支路电流。通过设置循环计算，可以获得所有GFLs 的故障电流矩阵。计算所有假设故障点的电流能量值，并求解最大电流能量值对应的点，该点为闪络故障点的参考位置。

步骤4：通过接近度修正系数将故障距离优化修正至最近杆塔位置上，此时的杆塔位置即为闪络故障定位的最终结果。

4 应用实例

4.1 不同采样频率

以国内某实测数据为例，对本文所提方法进行验证。设置FDTD 算法时间步长为1 μs，空间步长为10 m。对于采样波形通过1 kHz 的高通滤波器进行处理。

如图4 所示，截取的故障测距结果中仅含一个能量峰值，由于线路中传播的行波由不同频率组成，行波的色散使其在线路的传播过程中发生畸变，各频率不断衰减，传播距离越远，高频分量越少。因此图4 中仅有1 个局部最大峰值，能量聚焦在21.12 km 处。此外图4 还给出了不同采样频率下的FDTD 电磁时间反转测距结果，可以看出所提方法不受采样频率的限制。

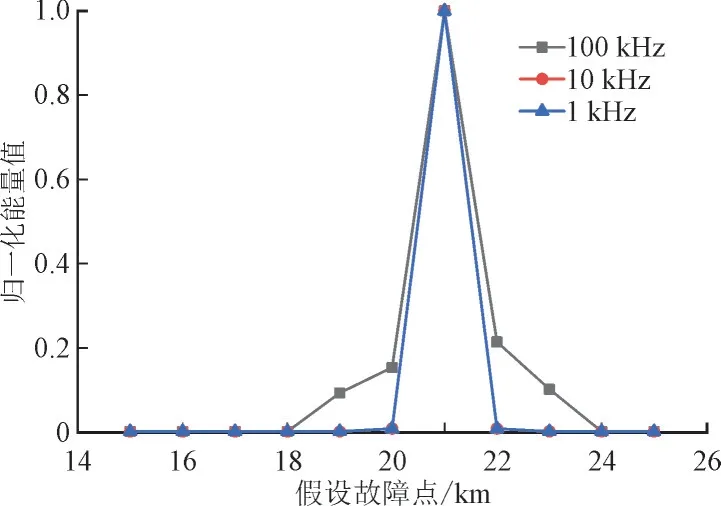
图4 不同采样频率下的测距结果Fig.4 Fault location results under different sampling frequencies

4.2 不同采样时间窗

时间窗作为测距阶段的重要因素，时间步随着时间窗的缩短而减少。图5 显示了电磁时间反转测距时不同时间窗下的电磁能量分布示意图。

图5 不同时间窗电磁时间反转测距结果Fig.5 Electromagnetic time reversal ranging results in different time windows

可以看出，随着所取时间窗越长，其电磁能量峰值越集中，故障点周围的峰值逐渐变窄，能够更好地观察到测距结果。相反的是，缩短时间窗能够更精细地描绘能量分布，减小误判范围的扩大。然而，当时间窗小于0.05 ms 时，测距结果出现较大误差，过小的时间窗导致录波装置无法及时捕捉瞬态信号。考虑到工程实践中的监测装置的高频采样率，选取1～5 ms 的时间窗是较为合适的。

4.3 测距结果优化

对FDTD 电磁时间反转测距结果进行修正优化，首先对最近邻地闪记录以及与参考故障点之间空间位置的坐标进行归算，求得相近杆塔编号，根据接近度修正系数得出优化结果，表1 给出了验证结果。

表1 故障测距优化结果Table 1 Fault location optimization results

根据现场检修人员的巡线结果，在杆塔均发现避雷器被击穿。优化结果存在一定误差，考虑原因为故障点之前的分支线路上存在经配电变压器连接的三相不平衡负载，会先于故障点发生反射。综上可以看出闪络故障优化的测距结果能够较为准确地反映故障位置。

5 结论

针对工程实践中配电网闪络故障工程实践数据量较大，故障行波标定困难，仅依靠行波测距难以判定雷击杆塔的情况，提出一种FDTD 电磁时间反转与地闪记录相结合的测距方法，并通过实测数据验证了方法的有效性。

1）仅在故障位置处存在能量峰值，不同采样率下测量故障信号均不会影响算法的稳定性。

2）适当增加电磁时间反转的时间窗口或减小FDTD 的空间步长，能够使得故障点周围的峰值变窄，提高测距精度。

3）以电磁时间反转测距的故障结果为参考，结合地闪记录的空间分布趋势，建立接近度修正系数，将距离优化至最近杆塔位置。