计及需求侧管理的新能源微电网多目标优化调度方法
王书峰,钟 明,许贤泽,包小千
(1.国网保定供电分公司,河北保定 071000;2.武汉大学电子信息学院,湖北武汉 430072)
0 引言
风力发电、光伏发电等新能源发电的快速发展是实现能源转型的重要举措[1]。受风力发电、光伏发电的不可控性和远距离输电损失等因素制约,新能源发电存在消纳不足的问题[2-3]。分布式发电(Distributed Generation,DG)技术是发展新能源的重要手段,增加了新能源发电方式的灵活性。微电网(Micro-grid,MG)将分散的DG 联系起来组成小型的独立发配电系统,既能提高供电质量,又能实现新能源发电的就近就地消纳[4]。MG 调度通过合理安排MG 内电力设备的发电功率,可在保障发电安全的前提下最大化效益。且需求侧的负荷作为特殊的调度资源可通过微电网参与电力系统调度,提高了电力调度的灵活性。需求侧管理[5][6(]Demand Side Management,DSM)是用户负荷参与MG 调度的手段,制定合适的DSM 策略调整用户用电模式能够提高MG 的运行效益和用户的收益。因此建立考虑DSM 的MG 调度模型有利于提高新能源消纳和MG的运行效益。
MG 调度的相关研究有很多,文献[7]建立了并网和孤网两种状态下的MG 经济调度模型。文献[8]考虑DG 的功率特性,实现了日前和日内两种时间尺度的MG 经济调度。文献[9]考虑了储能系统平滑DG 的作用,以最小化经济成本获得了储能系统的容量最优配置。文献[10-11]以经济性和环保性为优化目标,建立了MG 多目标调度模型。目前MG 使用较多的DSM 策略是需求侧响应,即通过分时电价或激励机制刺激用户改变用电习惯。文献[12]通过分时电价和奖惩机制改进用户用电模式,减少了用电高峰期的用电量,节约了电力资源。文献[13]通过对MG 内可中断负荷和可转移负荷的控制,提高了MG 对风电的消纳量。然而需求侧响应存在响应延迟大、可控性和智能性差等缺点,不符合智能电网的建设规划。因此提出了基于智能电网技术的DSM 策略,智能电表直接控制用户可控设备接入电网的时间,在保证用户用电需求的前提下改善用电结构。文献[14]建立了智能电网多种可控设备负荷转移的优化模型,以用户购电成本最小为优化目标进行优化,实现了负荷的削峰填谷。文献[15]将文献[14]提出的DSM 策略应用到MG 调度中,降低了MG 的运行成本。MG 调度模型是一个多维和多约束的非线性问题,传统的优化算法在求解时存在计算复杂度高、维数灾难等问题[16],因此目前的研究多采用启发式算法求解此类模型[17-18]。
为了提高MG 的新能源消纳以进一步提升其运行效益,本文首先建立了基于智能电网中多种可控设备负荷转移的DSM 多目标优化模型改善负荷结构,然后在此基础上以经济性和环保性为优化目标建立了新能源MG 多目标优化调度模型,最后改进了多目标粒子群优化算法(Multi-Objective Particle Swarm Optimization,MOPSO)来求解模型。在典型MG 算例中进行仿真分析,验证了本文所提的微电网调度模型的有效性。
1 需求侧管理多目标优化模型
本文采用基于MG 内可控用电设备负荷转移的DSM 策略实现MG 用电负荷的优化控制,以提高新能源消纳、降低用户购电成本和平抑负荷为目标,以多种可控设备的用电需求为约束条件,建立DSM多目标优化模型。
1.1 目标函数
1)以提高新能源消纳为优化目标控制需求侧可控设备的接入,当风力发电和光伏发电不足时减少用电负荷,发电充足时增加负荷,能够提高微电网用电负荷与新能源发电的适配度。优化目标函数F1如下所示:

式中:τ为1 d 划分的总时间间隔数;PL(t)为t时刻实际的用户负荷;R(t)为t时刻风光的预测出力之和。
由式(1)可知,新能源利用率越高时F1值越小。
2)通过需求侧管理策略在用电高峰期减少用电设备的接入,在用电低谷期增加用电设备的接入,既能减少用户的用电成本,又能平滑用电负荷曲线。优化目标函数F2如下所示:

式中:p(t)为t时刻的电价。
3)由于用电高峰期电价高而低谷期电价低,则F2会导致用电高峰期的用电量减少而低谷期用电量增加。为预防峰谷互换,以负荷峰谷差作为目标函数可保证用电负荷的平滑性。优化目标函数F3如下所示:

3 个目标函数中t时刻实际的用户负荷PL(t)由不可控和可控负荷组成,其数学表达式为:

式中:FL(t)为t时刻的负荷预测;CL(t)为t时刻接入的可控负荷;DL(t)为t时刻转出的可控负荷;L为可控设备的种类;ml为第l种可控设备的最大转移时间;Nlst为第l种可控设备由s时刻转移到t时刻的设备数量;Nlts为第l种可控设备由t时刻转移到s时刻的设备数量;Nls(t-k)为第l种可控设备由s时刻转移到(t-k)时刻的设备数量;Nl(t-k)s为第l种可控设备由(t-k)时刻转移到s时刻的设备数量;Pl1为第l种可控设备在开始时刻的负荷;Pl(k+1)为第l种可控设备在(k+l)时刻的负荷;dl为第l种可控设备所需负荷的时间。
1.2 约束条件
考虑实际负荷转移情况和可控设备用电需求的限制,所述DSM 多目标优化问题需满足如下约束条件:
1)任意时刻转移的可控设备数量为非负数:

2)任意时刻转移的可控设备总数量不超过该时刻可控设备的总数量:

式中:NC(s)为s时刻有用电需求的可控设备总数。
3)每种可控设备连接时间超过所需时长时断开连接:

式中:Pl(t-k+1)为第l种可控设备在(t-k+1)时刻的负荷。
4)可控设备负荷只能按照时序由之前时刻转移到其后时刻,且转移时间跨度不能超过上限:

在式(7)—式(11)约束条件下,以1 d 内各时刻可控设备的接入数量为决策变量,求解min{F1,F2,F3}问题,可获得在用户侧可控设备的参与下满足期待目标的真实负荷曲线以及微电网内的可控设备在1 d 内不同时刻的接入情况。
2 新能源MG经济环境优化调度模型
本文建立新能源MG 模型如图1 所示,包括风力发电(Wind Turbine,WT)、光伏发电(Photovoltaic,PV)、柴油发电机(Diesel Generator,DE)、微型燃气轮机(Micro Turbine,MT)、储能设备(Batteries,BAT)及可控负荷,MG 通过主隔离器与大电网连接,当MG 产能不足时可向大电网购电[19]。以经济性和环保性为优化目标建立该MG 的调度模型[20-21]。

图1 MG组成示意图Fig.1 Diagram showing composition of MG
2.1 目标函数
1)为改善台区微电网运行的经济效益,台区微电网调度的经济目标用台区微电网的运行成本Copt表示,包括传统分布式电源的燃料成本、分布式电源和储能系统的运行维护成本以及台区微电网通过联络线与大电网交互的成本。优化目标Copt表达式为:

式中:Ng为MG 中DG 的数量;T为1 d 划分的时间间隔总数;Cfuel,j(t)为第j个DG 在t时刻的燃料成本;Com,j(t)为第j个DG 在t时刻的运维成本;Cgrid(t)为MG 在t时刻与大电网交互的成本。
微电网的燃料成本具体表示为:

式中:CMTf为MT 的燃料成本;C为天然气的单价;LHV 为天然气的低热值;PMT为MT 的输出功率;ηMT为MT 的输出效率;CDEf为DE 的燃料成本;PDE为DE 的输出功率;α,β,γ为DE 的燃料成本系数。
MG 中电力设备的运维成本通常与电力设备的输出功率有关,计算公式如式(16)、式(17)所示。

式中:ζj为第j个DG 的运行维护成本系数;PDG,j(t)为第j个DG 在t时刻的输出功率。
MG 运行在并网状态,当发电单元发电不足时会向大电网购电,此时的交互成本为:

式中:Cbuy(t)为t时刻微电网向大电网购电的电价;Pgrid(t)为t时刻微电网与大电网的交互功率。
2)以新能源MG 排放的污染气体总量的治理成本Cplut作为环境成本,使其尽可能小。优化目标Cplut表达式为:
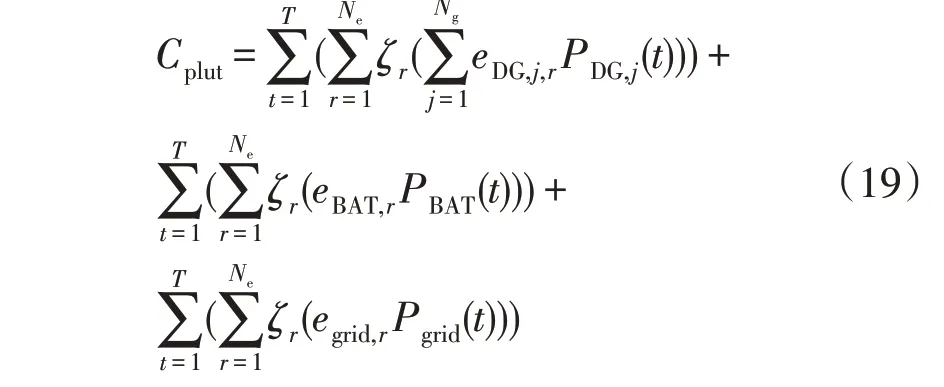
式中:Ne为污染气体种类;eDG,j,r,eBAT,r,egrid,r分别为第j个DG、储能系统和大电网排放第r种污染气体的系数;PBAT(t)为储能系统在t时刻的输出功率;Pgrid(t)为大电网在t时刻的输出功率;ζr为第r种污染气体的治理成本系数。
2.2 约束条件
1)潮流约束:

式中:Pnew(t),PLoad(t)分别为t时刻的新能源发电功率、用户的负荷总量。
2)DG 及大电网出力的功率约束:

3)DG 及大电网出力的爬坡约束:

4)储能系统运行约束:

5)旋转备用约束:

在式(20)—式(26)约束条件下,以MG 1 d 内各时间段分布式电源的输出功率、储能系统的充放电功率、MG 向大电网的购电功率作为决策变量,求解min{Copt,Cplut}的多目标优化问题,即MG 调度的数学模型。本文计及DSM 的新能源MG 调度流程示意图如图2 所示。
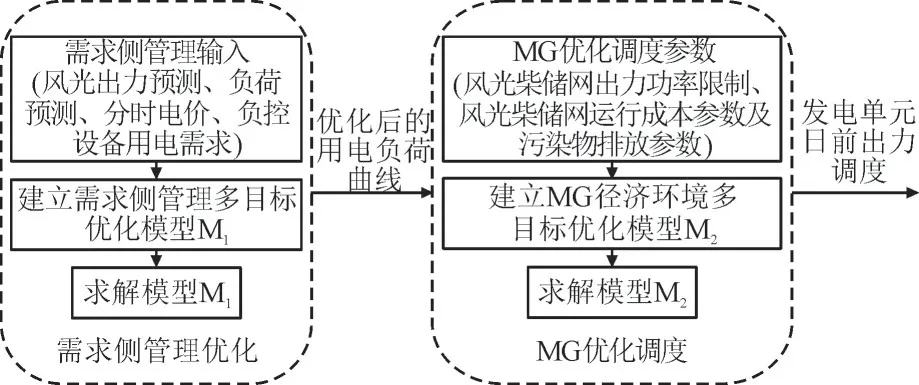
图2 MG调度模型框架Fig.2 Proposed framework of MG scheduling model
3 改进MOPSO求解模型
3.1 MOPSO
粒子群优化(Particle Swarm Optimization,PSO)是一种受鸟类觅食启发的随机搜索算法。MOPSO 算法将Pareto 支配概念引入基本的PSO 中[22],可以求解多目标优化问题,采用精英外部存档法保存当前非支配解集[23-24],并从当前非支配解集中选取粒子的pgbest。
3.2 基于目标空间分解和Maximin选择的MOPSO
MOPSO 求解时存在粒子多样性差、易陷入局部最优解的问题[25-26]。分解目标空间法[27-28]使粒子分布更加分散,可提升粒子多样性和全局搜索能力。
选取 1 组相对于参考点的方向向量E={e1,e2,…,en}将目标空间均匀分解为n个子空间(Ω1,Ω2,…,Ωn),每个粒子唯一地属于某个子空间,由粒子相对于参考点的方向向量与子空间方向向量之间的夹角决定:

式中:λ(pi(t))=[λ1(pi(t)),λ2(pi(t)),…,λM(pi(t))]为粒子的目标向量相对于目标参考点的方向向量。

对E中的任意方向向量ej,若有<λ(pi(t)),em>≤<λ(pi(t)),ej>,则第i个粒子的归属空间是em决定的子空间Ωm。
分解后的MOPSO 分别维护各子空间的非支配解集,粒子从所属的子空间中选取全局最优解。当非支配解个数超过档案容量R时,需在保持非支配解集多样性的前提下淘汰多余解。Maximin 函数[29]既能表达粒子的支配关系也可以表示支配程度,可用来维护外部精英档案。第i个粒子的Maximin 值fmm(pi(t))表示为:

式中:i,j=1,2,...,N;k=1,2,...,M。
因此每个非支配解的fmm为负数,fmm还可以表现粒子的多样性,非支配解的fmm值越小表示粒子越分散,即多样性越好。考虑目标函数的数量级不同,对粒子的目标函数值进行归一化处理后代入式(29)计算得到粒子的fmm值。当子空间的精英档案超出容量时,淘汰fmm值最大的粒子直至粒子数等于档案容量。
4 算例分析
为验证本文的模型和方法,以典型的MG 结构作为研究算例,设计了3 个MG 调度案例:(1)不考虑DSM 的情况下建立MG 调度模型;(2)构建以用户购电成本最小为目标的DSM 优化模型优化负荷并建立MG 调度模型;(3)构建1.1 节所述的DSM多目标优化模型并建立MG 调度模型。采用3.2 节提出的改进MOPSO 算法求解模型。图3 是算例MG 典型日的负荷需求及风力和光伏发电曲线。

图3 负荷预测和风光出力预测Fig.3 Forecast of load,WT and PV
表1 给出了MG 内可控设备的类型及相应的负荷需求,其中ts表示预设接入时间,tm表示最大转移时间,n表示设备数量;第1、第2、第3 时段分别表示该设备在设定的3 个时段的用电量。

表1 可控设备参数Table 1 Parameters of controllable devices
4.1 需求侧管理优化模型仿真分析
分别求解单目标和多目标DSM 优化模型,得到负荷曲线变化如图4 所示。由图4 可知,DSM 优化前的负荷曲线与购电成本最小负荷曲线及新能源出力曲线都相差较大,DSM 单目标优化后的负荷与购电成本最小曲线更贴合,而DSM 多目标优化后的负荷在贴近购电成本最小曲线的同时也与新能源出力曲线相匹配,且比DSM 单目标优化的负荷更加平稳。

图4 DSM优化前后负荷曲线Fig.4 Load curves before and after DSM optimization
DSM 优化前后可控设备在1 d 内的连接情况如图5 所示。由图5 可知,DSM 优化前可控设备连接具有无序性,在电价较高的阶段(也是用电高峰期)设备连接较多。经过DSM 单目标优化后,设备的连接时间和数量与分时电价相匹配,使得用户的购电支出更小。经过DSM 多目标优化后,设备并不完全与分时电价相匹配,而是同时配合新能源出力曲线以及更均匀地分布在各时间段连接。

图5 优化前后各时刻可控设备的连接数量Fig.5 Connection quantity of controllable equipment at each time before and after optimization
4.2 MG调度模型仿真分析
分别将无DSM 优化、DSM 单目标优化和DSM多目标优化后的负荷代入MG 经济环境调度模型求解,得到24 h 的MT,DE,BAT 和大电网出力情况如图6 所示。由图6 可知,无DSM 优化情况的MG 中传统发电单元的发电压力较大且储能系统的充放电压力较大,经DSM 优化尤其是DSM 多目标优化后的MG 中非清洁能源的发电压力明显减小。

图6 可控设备的连接分布Fig.6 Connection of controllable devices
MG 经DSM 优化调度后的相关指标如表2 所示,其中加粗体表示最优指标,可见考虑DSM 多目标优化后的微电网调度结果的经济成本、环境成本、“弃风光”电总量及负荷峰谷差都有明显减小。

表2 MG优化调度结果Table 2 Optimal scheduling results of MG
新能源出力的利用情况如图7 所示。由图7可知,在无DSM 优化时,由于新能源出力与负荷需求时间和规模不匹配,因此新能源出力的利用率较低,“弃风弃光”总量较大,因此传统的DG 出力以及MG 从大电网的购电总量较大。

图7 新能源利用情况Fig.7 Utilization of renewable energy
3 种场景下采用改进MOPSO 算法求解的Pareto 前沿如图8 所示。由图8 可知,DSM 单目标优化后MG 调度的经济和环境成本比无优化的情况有明显减小,而考虑DSM 多目标优化后MG 调度的经济和环境成本相较于另外2 种场景都有明显的减小。
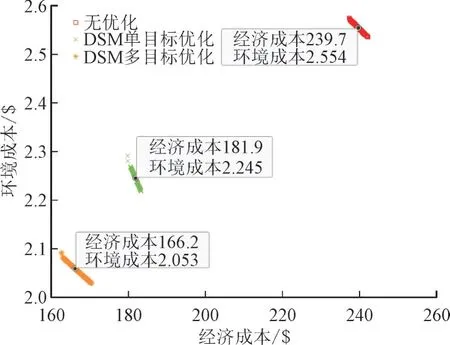
图8 Pareto 前沿Fig.8 Pareto front by improved MOPSO algorithm
5 结语
本文提出了一种考虑需求侧管理的新能源MG多目标优化方法。首先考虑新能源利用率、用户购电成本和负荷平稳性建立了基于可控设备负荷转移的DSM 优化模型,然后考虑经济性和环保性两个目标,建立了MG 调度模型。算例结果表明考虑DSM 多目标优化的MG 调度模型能够有效降低用户的购电支出,提升了新能源的利用率,缓解了MG内发电单元的发电压力和储能系统的充放电压力,从而进一步降低了MG 运行的经济和环境成本,提高了其运行效益。

