计及可用输电能力的风电并网系统中STATCOM的双层优化配置

陶然，张涛，2，冉华军，刘伉，王清川，黄明娟

（1.三峡大学电气与新能源学院，湖北宜昌 443002；2.智慧能源技术湖北省工程研究中心（三峡大学），湖北宜昌 443002）

0 引言

风电作为近年来大力发展的清洁可再生能源，具有良好的开发潜力[1-2]。随着大规模风电并网下电网中风电接入比例的提高，其功率波动对接入地区电网的可用输电能力（Available Transfer Capability，ATC）[3-4]及系统稳定性造成了不利影响。静止同步补偿器（Static Synchronous Compensator，STATCOM）[5-6]是柔性交流输电系统（Flexible AC Transmission System，FACTS）[7]设备中应用较为广泛的一种设备，具有灵活、快速的无功补偿能力，从而达到调整系统节点电压等运行参数的目的，有利于提高大规模风电接入下系统对电压和潮流的控制能力。因此其配置策略对提高系统稳定性与可用输电能力具有关键性影响。

目前对STATCOM 等FACTS 设备的优化配置已有一定研究。文献[8]采用灵敏度分析法确定STATCOM 等FACTS 设备的安装位置，对安装容量进行优化，结果表明FACTS 设备容量的适当配置能同时改善系统可靠性和经济效益。文献[9-10]针对多FACTS 设备配置场景，分析STATCOM 与晶闸管控制串联电容器（Thyristor Controlled Series Capacitor，TCSC）等不同种类FACTS 设备混合安装对系统的补偿影响，结果表明合理的组合方式能在保证补偿效果的同时兼顾经济性。文献[11]考虑无功设备的动作次数，采用基于原-对偶内点法的两阶段优化方法求解计及统一潮流控制器的无功优化问题。文献[12]以海洋捕食者算法、飞蛾扑火算法等多种智能优化算法求解FACTS 设备配置问题，得到不同算法对于此类混合整数非线性规划问题的求解效果。文献[13-14]计及系统的可用输电能力，以静止无功补偿器、STATCOM 和TCSC 等FACTS 设备为优化配置对象，通过改进算法全局搜索与局部搜索能力来提升寻优效率，并使最终配置结果更优。

针对现有文献在进行FACTS 设备选址定容时较少考虑风电的不确定性，本文计及风电不确定性，建立以可用输电能力、静态电压稳定指标和投资成本的STATCOM 双层优化配置模型。下层模型根据上层规划结果以原对偶内点法计算基态下的最优潮流，上层模型根据下层运行结果以多目标灰狼粒子群算法（Multi-objective Grey Wolf Particle Swarm Optimizer，MOGWPSO）评估不同STATCOM安装位置与容量下的风电并网系统可用输电能力等指标。通过对多目标灰狼算法添加混沌初始化步骤和引入粒子群算法中的速度计算方式，并基于网格法选取群体中的领导者，来增加解空间中解的多样性并减少算法陷入局部最优现象。算例分析验证了本文提出模型与算法的有效性。

1 计及可用输电能力的STATCOM双层优化配置模型

1.1 风电数学模型

风电具有很强的不确定性与波动性，一般用威布尔分布来模拟风速的概率分布[15-16]。风电出力的概率密度函数如式（1）所示：

式中：v为风速；k为形状参数；c为尺度参数。

风电有功出力Pwt与风速v之间的关系如式（2）所示：

式中：Prate为风机额定功率；vin，vrate，vout分别为切入风速、额定风速、切出风速。

1.2 STATCOM数学模型

STATCOM 由耦合变压器、换流器和直流电容器组成，其结构图如图1 所示。STATCOM 并联到系统中时，能有效地对接入侧节点进行无功补偿，从而降低电网电力传输损耗，潮流计算中可采用等效功率注入模型，将STATCOM 等效为1 个理想无功功率源，从系统中注入或吸收无功功率。设QS为STATCOM 向系统注入或吸收的功率，表示为ΔQ=QS。

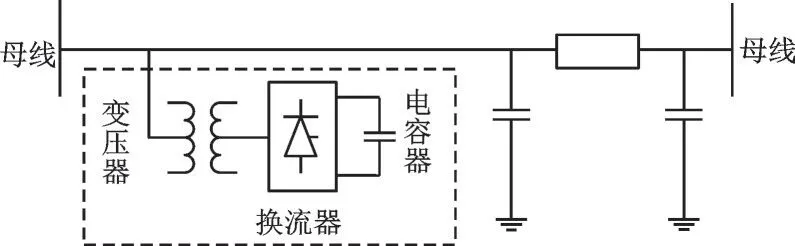
图1 STATCOM结构图Fig.1 Structure diagram of STATCOM

1.3 上层优化模型

1.3.1 目标函数

上层优化模型是在下层模型调度发电机组优化运行问题并确定现存输电协议量（Existing Transfer Capability）（量值为JETC）的基础上，来求解系统可用输电能力JATC，L指标及STATCOM 投资成本等目标。计算ATC 时以发电区中所有发电机组相对于基态有功出力增量的最大值为目标；L指标反映了系统静态电压稳定性，其值在[0，1]间，越接近0则电压稳定裕度越大[17]。各目标函数表达式如下：

1）目标1：系统可用输电能力JATC最大，即：

式中：PGξ，αGξ为送电区节点ξ处的发电机有功出力及其增长因数；NPV为送电区PV 节点个数；PG0为送电区发电机出力总值，通过下层模型计算最优潮流后求出。

其中，取负以将最大值为优问题转化成以最小值为优。

2）目标2：静态电压稳定指标L指标最小，即：

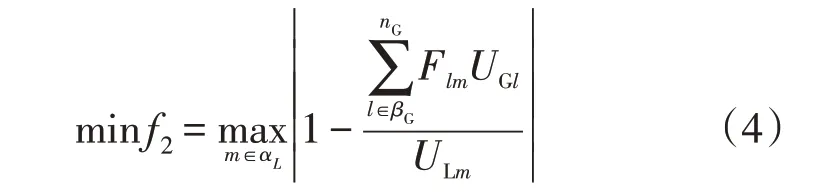
式中：UGl，ULm为发电机节点l的电压和负荷节点m的电压；αL，βG为负荷节点与发电机节点集合；nG为发电机节点个数；Flm为负荷参与因子。

3）目标3：STATCOM 投资成本最小，即：

式中：s为STATCOM 补偿容量成本。

1.3.2 约束条件

1）功率平衡约束：

式中：PGi，QGi为发电机有功、无功出力；Qwt为风电无功出力；PLi，QLi为负荷有功、无功功率；λLi为负荷增长因数；Ui，Uj为节点i，j电压；θij为节点i，j电压相角；Bij，Gij为节点i，j间的电导与电纳。

2）控制变量与状态变量约束，包含STATCOM 安装位置与容量约束、发电机有功、无功出力约束、负荷增长因数约束、节点电压约束、支路传输功率约束等：

式中：BS，QS为STATCOM 安装位置与容量；Pij为线路传输容量；下标max，min 表示变量上下限。

1.4 下层优化模型

1.4.1 目标函数

下层优化模型是在上层模型确定STATCOM 位置与容量配置的基础上，以发电成本最低为目标来求解系统基态时的最优潮流。系统基态运行下的各节点功率分布决定了后续可用于交易的传输容量[18]。目标函数表达式为：

式中：a，b，c为火电机组煤耗成本；CG为火电机组发电成本。

1.4.2 约束条件

1）功率平衡约束：

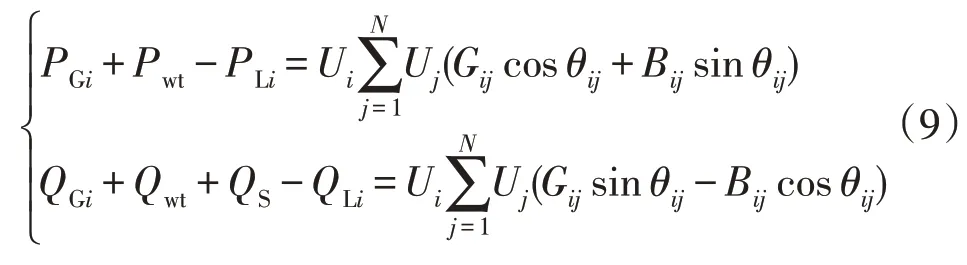
2）控制变量与状态变量约束，包含STATCOM容量约束、发电机有功、无功出力约束、节点电压约束、支路传输功率约束等：

式中：Q′Smax，Q′Smin为系统基态运行时的STATCOM无功出力最大值与最小值，由上层模型的QS确定，即下层模型的无功出力不能超过上层模型给定的补偿容量。

2 双层优化配置模型的求解

2.1 模型流程

本文所提出的STATCOM 双层优化配置模型如图2 所示。首先采用拉丁超立方抽样[19]生成1 000个初始场景，再利用后向削减法[20]，得到最终所需的典型场景。上层模型采用MOGWPSO 算法，下层模型以原对偶内点法[21]进行求解。

图2 双层优化配置模型流程图Fig.2 Flow chart of bi-level optimal configuration model

2.2 求解算法

2.2.1 MOGWPSO算法

多目标灰狼算法（Multi-objective Grey Wolf Optimizer，MOGWO）是在灰狼算法[22]基础上为求解多目标优化问题提出的多目标优化算法。针对MOGWO 较易陷入局部最优问题，本文提出改进的MOGWPSO 算法。一般多目标优化问题中常采用的方法有分解法、拥挤度排序法、网格法和参考点法等，本文采用基于网格法的MOGWPSO 算法，步骤如下：

1）初始化种群，种群中每个元素x代表1 个决策变量：

式中：m为种群大小；n为个体长度。

2）对初始种群进行Tent 混沌初始化，良好的初始种群能使算法寻优效率更佳，采用Tent 混沌映射能使初始种群中变量具有良好的随机性和均匀分布特性，其映射方程为：

式中：μ为[0，1]间的数，本文取0.49；Z(t)及Z(t+1)为混沌序列。

3）选出α狼、β狼、δ狼3 只头狼。对初始种群进行目标函数计算，进行非支配排序以得到Pareto解集，存入Archive 集中并从中创建网格，根据网格中个体数量大小按轮盘赌的方式从中选出头狼，其中网格中个体数量越小，被选中概率越大。以二目标优化问题为例（f1，f2为目标函数），如图3（a）所示。

图3 算法流程示意图Fig.3 Schematic diagram of algorithm flow

4）捕猎过程。以3 只头狼为领导者，向头狼

的位置移动而靠近猎物的过程。

式中：C1，C2，C3为[0，2]间的随机数；A1，A2，A3为[-a，a]间的随机数，a为由2 线性递减至0 的收敛因子；Xα，Xβ，Xδ为α狼、β狼、δ狼位置。

为减少陷入局部最优现象，将如式（15）所示的粒子群算法中的粒子飞行速度计算公式添加到MOGWO 中，给予MOGWO 算法1 个速度惯性来增大其搜索范围。因此，MOGWPSO 的位置更新公式变为式（16）：

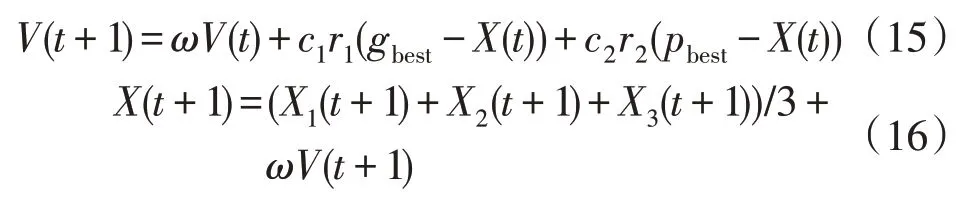
式中：c1，c2为学习因子；r1，r2为[0，1]间的随机数；gbest，pbest为全局最优与历史最优的个体位置；ω为线性递减的收敛因子。

通过调整ω大小使前期具有一定的速度以维持全局搜索，后期逐渐减小该速度，增加局部搜索精度，以平衡算法的全局搜索与局部搜索。

5）获得新的Archive 集。对个体的位置计算适应度，进行非支配排序以选出Pareto 解集，将其加入Archive 集中，再对加入后的Archive 集进行非支配排序，若Pareto 解集个体数量超出Archive 容量，以轮盘赌方式剔除部分个体，再划分新的网格，其中单个网格中个体数越多被选中概率越大，如图3（b）所示。

为从算法最终得到的Pareto 解集中选取1 个折衷解便于后续分析，本文采用熵权法确定解集中各个目标的权重，再利用逼近理想解排序法来从中选出折衷解，详见文献[23]。

2.2.2 原对偶内点法

原对偶内点法常用于解决电力系统最优潮流等非线性规划问题，其通过引入松弛变量来将不等式约束转化成等式约束，并添加障碍函数，构建拉格朗日函数，再以牛顿法求解非线性方程组，得到每次迭代的步长来修正变量，当对偶间隙小于给定值时停止迭代并输出结果。

3 算例分析

3.1 建立模型

使用Matlab 软件在IEEE 30 节点系统上进行仿真，如图4 所示，将IEEE 30 节点分为送电区、受电区和其他区域。

图4 IEEE30节点图Fig.4 IEEE 30-node system

节点8 接入1 个容量为30 MW 的风电场，其中每台风电机组的额定容量为1.5 MW，风机切入风速为3 m/s，额定风速为10.8 m/s，切出风速为25 m/s，功率因数为0.95，风电场总装机容量约占系统总发电量的10%。系统基准容量为100 MVA，各节点电压上下限为[0.94 p.u.，1.06 p.u.]，STATCOM 容量上下限为[-100 Mvar，100 Mvar]。

形状参数k取2.2，尺度参数c取15 m/s，使用后向削减法得到4 个场景的风电功率比例及其对应场景概率，如表1 所示。

表1 风电功率场景表Table 1 Wind power ratio and probability corresponding to four scenarios %

3.2 结果分析

利用MOGWPSO 算法得到4 个典型风电场景下STATCOM 的安装位置与补偿容量，如表2 所示。

表2 不同场景下配置结果Table 2 Configuration results of STATCOM under four scenarios

不同场景下STATCOM 的安装位置也有所差别，当风电功率越大时，为使系统保持安全运行而补偿的容量也更大；同时结合表1 可知，场景4 的概率在所有典型场景中最大，因此可选择概率最大的场景4 的配置方案作为选择。

不同场景下安装STATCOM 与不安装时系统ATC 与L指标的优化结果如图5 所示。

图5 各场景优化结果Fig.5 Optimization results of each scenario

由图5 可知，系统JATC随着不同风电场景下风电功率的增长而变大，L指标则略微减小，从场景1风电功率为0 到场景4 风电保持额定功率运行时，系统的JATC从39.785 8 MW 提升到了52.546 8 MW，增加了32.07%，说明风电接入后能在保持电压稳定下有效提升系统的可用输电能力。对比安装STATCOM 和不安装的情景下，可知安装设备后每个场景系统的JATC和L指标都得到了有效改善，JATC在4 个场景中相对于未安装时提高了18.1%～29.4%，L指标降低了5.4%～5.8%，说明安装STATCOM 不仅能有效提升风电接入时系统的可用输电能力，还能同时提高系统静态电压稳定性。

当维持系统某一运行状态控制变量不变，含STATCOM 与不含的系统运行时各节点的电压与L指标如图6 和图7 所示。

图6 各节点电压Fig.6 Voltage of each node

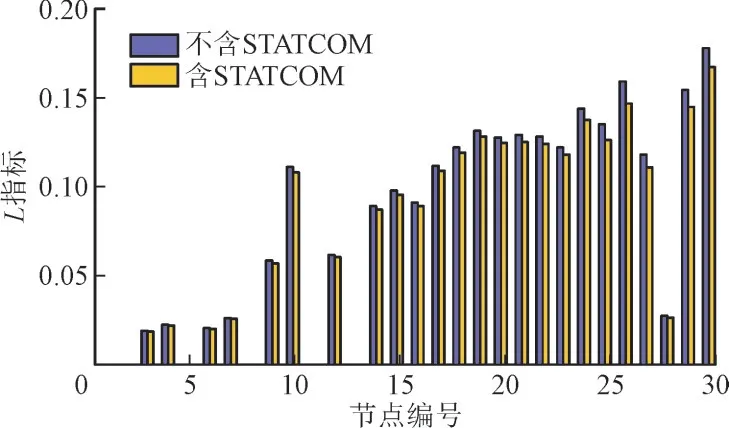
图7 各节点L指标Fig.7 L index of each node

从图6 可知，含STATCOM 的系统运行时由于其无功补偿作用，每个节点的电压均得到一定抬升，尤其对于受电区域中的节点。结合系统L指标图亦可分析出相似结论，因此含STATCOM 系统运行时具有更高的电压稳定性。

3.3 算法对比

以场景4 为例，对比算法改进前后性能，从解集中选取的折衷解如表3 所示。

表3 2种算法结果对比Table 3 Comparison of results between two algorithms

由表3 可知，MOGWPSO 得到的系统STATCOM补偿容量更小，相较于MOGWO，JATC更大、L指标和投资成本更小，而计算时间由343 s 降到了328 s，因此改进后使得算法的收敛速度变快，算法的寻优效率也得到了提升。

各算法得到Pareto 前沿如图8 所示。

图8 2种算法Pareto前沿Fig.8 Pareto frontiers of two algorithms

图8 中星形点为理想点[24]，Pareto 前沿中的点越靠近理想点则越优，因此图中MOGWPSO 所得到的解更接近真实Pareto 前沿。集合解集覆盖率[25]是评价一种算法所得的解对另一算法所得解的支配率，而MOGWPSO 对MOGWO 的集合解集覆盖率为0.918 9，即其中91.89%的个体要优于MOGWO，进一步验证了MOGWPSO 寻优效果更优。

为体现不同算法所得解的分布性，各算法在3个目标上的箱线图如图9 所示。图9 中JATC方向上，可知2 种算法分布性均较好，但MOGWPSO 数据范围更大，解集中多样性更佳，即能搜索到JATC更大的解；L指标方向上MOGWPSO 虽分布性劣于MOGWO，但数值整体上更小，结果更好；成本方向上所得解集分布性、范围与结果均好于MOGWO，综合比较下MOGWPSO 所得的数据更优。

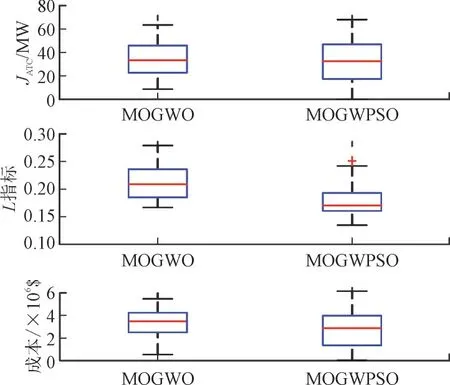
图9 2种算法箱线图Fig.9 Box plot of two algorithms

3.4 双层配置与单层配置对比

双层配置中STATCOM 上层为STATCOM 的规划层，下层为含STATCOM 的系统潮流优化层，因此在上层进行规划时，会考虑到下层系统运行时基态潮流下的ETC 的影响。相比于单层优化配置时，未对系统基态运行下的JATC进行优化，直接对STATCOM 容量与位置进行规划，双层配置下得到的结果更具有准确性与实际意义。对比双层配置与单层配置时4 个场景下的Pareto 前沿如图10 所示。

图10 单层配置与双层配置对比图Fig.10 Comparison of single-level configuration and bi-level configuration

从图10 可知，4 个场景下双层配置的Pareto 前沿均优于单层配置时的结果。场景1 到场景4 单层配置时得到的系统JATC最大值分别为37.85 MW、44.15 MW、48.92 MW 和54.18 MW，因此每个场景下双层配置得到的JATC均大于单层配置的情形；双层相比单层配置下L指标的最小值相差较小，但4个场景中双层配置下的L指标最大值分别为0.181 5，0.192 0，0.208 1 和0.231 3，相较于单层配置得到的0.212 3，0.228 9，0.237 9 和0.246 0 均有一定改善；最大投资成本在4 个场景下也下降了15.54-34.68%；相比单层配置，在STATCOM 的双层配置模型优化下得到的目标值结果更好。

4 结论

本文提出一种计及ATC 的STATCOM 双层优化配置模型，利用场景法模拟风电不确定性，采用内点法和改进的MOGWPSO 算法分别对下层和上层模型进行求解，并在IEEE 30 节点上进行算例分析。算例表明：

1）在考虑ETC 影响且对基态潮流进行优化的STATCOM 双层配置模型下，得到各目标函数的目标值优于STATCOM 单层配置的结果，更具工程意义。

2）风电接入和安装STATCOM 均能使系统的JATC得到提高或L指标得到降低，且安装STATCOM使系统在风电功率较低场景下可用输电能力也较低的情形得到改善，提高了风电送出能力。

3）所提出改进算法能有效改善陷入局部最优现象，从而获得更好的结果，且解也更具多样性，分布性更好。改进前后算法得到的配置结果进一步证明了STATCOM 合理的配置方案对提高风电并网系统的可用输电能力与电压稳定性具有重要意义。