兼顾频率变化率和偏移量的光储虚拟惯量联合控制策略研究

高本锋，刘佳敏，孟建辉，符章棋，王帅帅

（河北省分布式与微网重点实验室（华北电力大学），河北保定 071003）

0 引言

随着“碳达标、碳中和”政策的不断推进，光伏发电占比日益增长[1-2]。由于光伏发电系统通过电力电子器件实现并网，缺乏传统发电机所具有的惯性特点，因此，当系统频率出现波动时，光伏发电系统不能够及时缓解频率波动带来的稳定性问题[3-4]。近些年，以南澳“9.28”[5]，英国“8.9”[6]为代表的大停电事故，其本质原因是高比例新能源接入电力系统造成系统抗扰性变差，从而导致系统故障时有功功率供求关系严重失衡。因此，提高含新能源电网的惯量水平和一次调频能力显得尤为重要。

虚拟同步发电机技术（Virtual Synchronous Generator，VSG）能够模拟传统发电机的惯量特性，应用在光伏领域中可以提高系统的整体惯量和一次调频能力[7]。目前多数文献侧重于研究系统内部因素与VSG 控制之间的相互影响[8-11]，忽略了VSG 控制本身的调频特性，不利于进一步的研究。因此，有必要对VSG 控制本身的调频特性进行深入分析和优化改进。

现有的VSG 控制手段主要是在线性控制、棒-棒控制[12]和指数函数控制[13]的基础上进行优化改进。文献[14]分析了基于指数函数的VSG 控制优势，提出了灵活虚拟同步发电机控制（Flexible Virtual Synchronous Generator，FVSG）策略，该策略在频率下降过程中起到了明显作用。文献[15-17]采用的VSG 控制方法为线性控制，并结合下垂控制对虚拟惯量进行调节，有效减少了稳态频率偏差。文献[18]在棒-棒控制的基础上进行改进，提出一种虚拟同步机频率自恢复控制策略，该策略优化了频率的恢复特性。文献[19]将棒-棒控制与线性控制相结合，提出一种改进的转动惯量自适应控制（Improved Adaptive Control of Inertia，IACI）策略，该策略减少了VSG 并入微网过程中的有功振荡。上述文献均针对单独考虑频率变化率（Frequency Rate，FR）和频率偏移量（Frequency Offset，FO）时的VSG 控制进行研究，二者的调频效果各有优势。前者能够快速响应频率变化，缓解频率下降速度；后者则能够有效减少频率的最大偏差。

然而，FR 和FO 的单独使用均无法兼顾整个系统的频率稳定。仅考虑FR 的VSG 控制虽能够起到快速频率支撑的作用，但无法减小频率偏差；仅考虑FO 的VSG 控制尽管减小了频率偏差，但不能够有效抑制频率的下降速度。因此，文献[20-21]提出一种由FR 和FO 共同决定的自适应虚拟惯量控制方法，但该方法中FR 和FO 存在着矛盾关系，影响了惯量控制效果。文献[22-23]将虚拟惯量与下垂控制相结合，通过调整惯性系数和下垂系数，避免了频率下降与恢复过程中存在的冲突。文献[24]在文献[22]的基础上，通过改变VSG 控制中FR 和FO 的比例系数，解决了FR 和FO 之间的矛盾关系，但所提策略中比例系数的选取过程较为复杂，缺乏一定的实用价值。

本文统筹考虑调频过程中FR 和FO 的变化特点，提出一种同时兼顾FR 和FO 的虚拟惯量联合控制（Virtual Inertia Joint Control，VIJC）策略。该策略弥补了单独考虑FR 和FO 时VSG 控制的不足，并利用控制自身的变化特点，取代了FR 和FO 之间繁琐的比例系数选取过程，提高了VSG 控制的时效性。将所提VIJC 策略与单独考虑FR 和FO 的VSG 控制、文献[14]中的FVSG 策略、文献[19]中的IACI 策略以及文献[22]所提控制策略进行对比，验证了本文所提VIJC 策略的优越性。

1 虚拟惯量控制原理

本文以光伏附加储能装置的交流系统为研究对象，拓扑结构如图1 所示。其中，L和C分别为滤波器电感和电容，R1，X1分别为线路等效电阻和等效电抗。VSG 控制主要包括功率环模块和电压电流环模块。其中，逆变器输出的电压u0和电流i0通过功率环计算得到电压指令值u0*，并传递给电压电流环，功率环的计算公式如式（1）所示，其中，PWM 为脉冲宽度调制。

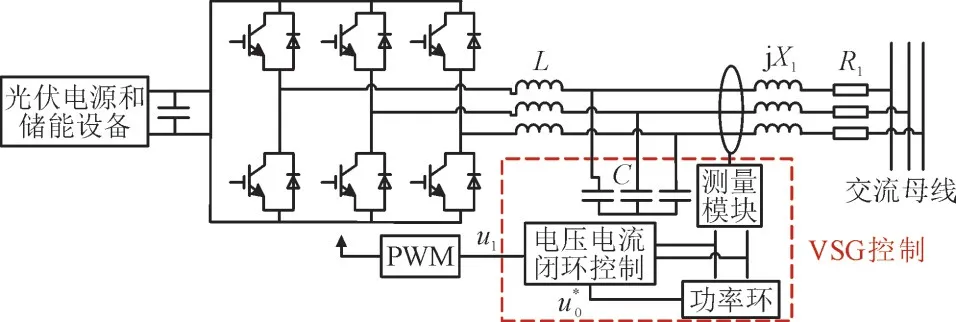
图1 PV-VSG控制结构图Fig.1 PV-VSG control structure

式中：Pref为有功功率参考值；P0为逆变器输出有功功率；Kd为阻尼系数；ω为VSG 控制输出的角频率；ωg为电网角频率；φ1为相位角；H为系统的虚拟惯量值。

电压电流环的控制框图如图2 所示，其输出的电压参考值u1经过PWM 技术生成控制信号，对逆变器进行控制。其中，Kpc，Kpv分别为电压环和电流环的比例系数；Kiv，Kic分别为电压环和电流环的积分系数，s为中间量，无实际意义。

图2 电压电流环控制框图Fig.2 Voltage and current loop control block diagram

由式（1）可知，调节H的值可以改变VSG 控制输出的角频率，进而改变着系统的功率和频率响应特性。以往研究表明，H越大，频率下降速度越慢，频率跌落幅度越小[13，16]。然而，H过大会影响系统频率的恢复特性，使频率不能较快恢复至正常状态。因此，H的大小需要根据VSG 控制进行合理调整，才能够得到较好的调频效果。

2 兼顾FR和FO的VIJC策略研究

考虑FR 的VSG 控制根据频率微分项来调整H的大小，能够快速响应频率的变化；考虑FO 的VSG 控制根据频率偏差项来调整H的大小，能够减小频率的最大偏差。两者各有优势，将其结合可充分发挥储能装置的调频效果。但FR 和FO 在调频阶段存在一定的矛盾关系，具体表现为：频率跌落初期，FR 最大，而FO 较小；频率下降至最低点时，FO 最大，而FR 较小。为此，本节提出一种兼顾FR和FO 的VIJC 策略。该策略能够充分发挥调频效果的VSG 控制方式，避免了调频阶段FR 和FO 之间存在的冲突；同时利用控制函数自身的变化特点，取代了FR 和FO 之间复杂繁琐的比例系数选取步骤，提高了频率响应速度。

由于FR 和FO 在频率变化过程中存在着矛盾关系，因此为建立两者之间的联系，构造评价FR 和FO 相对重要程度的评判指标m，如式（2）所示。

式中：σ为一极小值，防止Δf为0 导致评价指标无效；df/dt为某一时刻的频率变化率；Δf为该时刻的频率偏移量。

分析不同函数类型的变化特点可知，指数函数的增长速度较快，能够在短期内提供较多的惯量，改善频率的下降过程；反正切函数随着自变量的增大会无限逼近一固定值，在一定程度上限制了惯量的增加。因此，将一段时期内FR 和FO 中影响较大的一方采用指数函数控制，以快速响应频率的波动；影响较小的一方采用反正切函数控制，提供基础的惯量支撑，保证系统安全运行。

VIJC 策略的控制方程为：

式中：k1，k2分别为指数函数和反正切函数的控制参数，2 个参数均大于0；H0为虚拟惯量初值；H1为稳态时的虚拟惯量值；a为评价指标m的切换阈值。

当评价指标低于阈值a时，视为FR 为主导影响因素，因此对FR 采用指数函数控制，对FO 采用反正切函数控制；当评价指标在[a，0]区间时，视为FO 为主导影响因素，对FO 采用指数函数控制，FR采用反正切函数控制；当评价指标大于0 时，频率进入恢复阶段，此时应尽可能减少虚拟惯量来加快频率恢复，故采用1 个较小的常数值H1进行控制。

VIJC 策略下虚拟惯量变化如图3 所示，其中横坐标为时间，纵坐标为虚拟惯量大小。控制曲线可分为3 部分：由FR 主导的控制部分、由FO 主导的控制部分和频率恢复部分。曲线共有2 个峰值（Hmax1和Hmax2）和2 个谷值（Hmin1和Hmin2），第1 个峰值起到缓解频率突降的作用，第2 个峰值起到提升频率最低点的作用。ton，toff分别为VIJC 控制启动与结束时刻，t1为转折点。

VIJC 策略的流程图如图4 所示。其中，当电网频率f与额定频率（f0=50 Hz）的偏差超过最大允许偏差fma（x0.03 Hz）时，启动VIJC 策略。计算评判指标m的大小，当m小于阈值a时，采用以FR 为主导的VSG 控制；当m在[a，0]范围内时，采用以FO为主导的VSG 控制；当m超过0 时，频率进入恢复阶段，此时无需过多的惯量支撑，采用稳态时的常数控制（H=H1），使频率快速恢复至正常状态。

图4 VIJC策略流程图Fig.4 Flow chart of VIJC strategy

3 VIJC策略中的参数选取

3.1 参数k1的选取

根据第2 节可得，k1越大，提供的虚拟惯量越多，但k1的最大值应综合考虑储能装置的荷电状态和系统所需惯量的极限范围。已知系统的虚拟惯量值H＞4 时认为惯量充足，但一般不超过6[7，25]，因此取Hmax=6。计算式（3）中的2 个峰值，第1 个峰值在频率开始跌落时（如图3 中的Hmax1），此时近似认为Δf=0；第2 个峰值在频率跌落至最低点（如图3 中的Hmax2），此时近似认为df/dt=0。综上得到求取参数k1的约束条件如下：

由于Δf和df/dt存在着一阶导数关系，因此可将Δf和df/dt看作是复杂函数的因变量和自变量，即Δf=F（df/dt），F 为函数名。因此式（4）可看作将函数Δf=F（df/dt）限制在长度为R的正方形区域内，R的表达式如式（5）所示。

调频阶段，R应不小于频率允许偏差的最大值，以保证VIJC 策略能够在频率跌落阶段充分发挥调频作用。根据GB/T 1594—1995 的规定，电网额定频率为50 Hz 时，光伏系统并网后的频率允许偏差值为±0.5 Hz，因此R应不小于0.5。除此之外，R还应小于一次调频的最大持续时间30 s[26-27]。得到参数k1的取值范围为[0，2.3]，因此选取k1为2.3。

3.2 切换阈值a的选取

参数m的切换阈值a是根据特定工况下FR 和FO 之间的大小关系而定。根据频率变化曲线可知，频率调节过程中，曲线斜率的绝对值由最大值开始减小，直至为0。因此，为简化FR 和FO 两者关系，本文近似将曲线斜率看作随时间单调递减的一次函数，如图5 所示。

图5 调频阶段FR随时间变化曲线Fig.5 Variation curve of FR with time in frequency modulation stage

图5 中b为一次函数系数，该一次函数的横坐标为时间t，纵坐标为频率变化率FR 的绝对值|df/dt|，该曲线与x，y轴围成的面积为频率偏移量FO。

将图5 中的2 个公式带入式（2）得到m绝对值关于时间的函数表达式，如式（6）所示。根据频率允许偏差范围和一次调频的最大可持续时间，得到m绝对值关于时间的函数表达式的约束条件，如式（7）所示。联立式（6）、式（7）得到m的取值范围为[-0.5，0]，因此本文选取m的切换阈值a为-0.25。

3.3 参数k2的选取

参数k2的选取要保证调频阶段提供的虚拟惯量充足有效，即惯量曲线的最低点不能低于4[7，25]，式（3）中惯量曲线的2 个最低点出现在m为a时和m为0 时（分别如图3 中的Hmin1和Hmin2），因此参数k2的约束条件为：

联立式（6）、式（8）可得参数k2的取值范围为[0.43，0.84]，本文选取k2为0.8。

4 VIJC策略仿真验证

为验证所提VIJC 策略的可行性，在Matlab/Simulink 中搭建光储VSG 单元交流系统模型，将VIJC 策略与4 种经典控制及3 种具有代表性的控制策略进行仿真对比。系统拓扑图如图6 所示。

图6 含VSG单元的4端系统拓扑结构Fig.6 Topology of 4-terminal system with VSG unit

图6 中，同步发电机G1工作在恒功率模式，输出功率为PG1，以满足基本负荷需求；同步发电机G2负责系统二次调频，输出功率为PG2；P0为逆变器输出功率；光伏发电单元作为新能源发电单元发出恒定功率；蓄电池承担系统的能量双向流动，作为虚拟惯量支撑来源。

仿真参数如表1 所示，其中Ud为各VSG 单元中直流母线电压大小；UBAT为各蓄电池的额定电压，Kd为阻尼系数，τpm为燃油喷射系统时间常数，kpm为柴油发动机的增益与燃油喷射系统的增益之和，kL为发电机损耗系数，ωref为角频率参考值，JG2为发电机G2的转动惯量，Kp为PI 控制器比例增益，Ki为积分增益，τd为柴油发动机停滞时间的一半。仿真设置在15 s 时突增负荷5 kW，30 s 时切除负荷3 kW，光照强度恒为1 000 W/m2，蓄电池的初始荷电状态（State of Charge，SOC），其值为SOC=0.7。仿真观察VIJC 策略与其他控制方法下，系统频率f，DC/AC 逆变器输出功率P0以及储能荷电状态SOC的波形对比。

表1 4端交流系统参数Table 1 Parameters of 4-terminal AC system

图7 为单独考虑FR 和FO2 种情况下，VIJC 策略与棒-棒控制[12]、指数函数控制[13]、幂函数控制以及反正切函数控制的效果对比图。在系统频率变化方面，图7（a）采用VIJC 策略有效地减少了频率的最大偏差，优化了频率的恢复特性；图7（b）中，采用VIJC 策略提高了频率响应速度，减少了频率恢复阶段的波动。

在有功功率波动方面，从图7（a）和（b）可知，本文所提VIJC 策略能够有效减少有功功率的波动，且使功率较快地恢复至稳定状态。

在储能SOC 变化方面，从图7（a）和（b）可知，本文所提方法对应的SOC变化曲线均高于其他控制方法，这表明VIJC 策略有效利用了储能的惯量支撑能力，能够在优化功率和频率特性的同时，最大程度地减少了储能的过充和过放。VIJC 策略充分发挥了不同类型VSG 控制的优势，弥补了单独考虑FR 和FO 时VSG 控制的不足。

图7 VIJC策略与4种经典控制对比Fig.7 Comparison of VIJC strategy with four classical control strtagies

为了充分验证本文所提VIJC 策略的优越性，在所提仿真条件下，选取储能参与电网调频领域中具有代表性的3 种VSG 控制策略：单独考虑FR 时的FVSG 策略[14]、单独考虑FO 时的IACI 策略[19]以及兼顾FR 和FO 时的自适应控制策略[22]进行调频效果对比。图8 为3 种控制策略与VIJC 策略下的系统频率、逆变器输出功率以及储能SOC的波形对比图。

图8 VIJC策略与3种控制策略对比Fig.8 Comparison of VIJC strategy with three control strategies

在系统频率变化方面，从图8 可知，相较于IACI 策略和FVSG 策略，本文所提VIJC 策略能够有效降低频率的跌落幅度，显著优化了频率恢复特性；相较于文献[22]的自适应控制策略，本文所提VIJC 策略能够更快速响应频率的变化，使频率最先抵达最低点并平稳恢复至正常状态，提高了控制的时效性。

在有功功率波动方面，在15 s 和30 s 时，VIJC 策略下的有功功率波动起伏均最小，恢复速度最快。这表明相较于其他3 种控制策略，VIJC 策略能够更有效地抑制功率波动，提高了系统的暂态稳定性。

在储能SOC 变化方面，VIJC 策略与文献[22]的自适应控制策略下储能SOC值的下降幅度相似，但VIJC 策略下频率和功率的变化特性均优于自适应控制策略。这表明VIJC 策略能够合理利用储能提供的能量，保证在优化系统频率和功率特性的前提下，提高储能系统的利用率。

5 结论

本文针对光储并网系统提出一种综合考虑FR和FO 的VIJC 策略，并得到以下结论：

1）根据FR 和FO 之间的相对评价指标，将调频过程划分为以FR 为主导、以FO 为主导和频率恢复3 个阶段，取代了FR 和FO 之间繁琐的比例系数选取过程。

2）各阶段采用不同方式的VSG 控制，利用函数自身的变化特点，解决了FR 和FO 之间的冲突，提高了控制策略的时效性。

3）仿真结果表明，同等扰动条件下，本文所提VIJC 策略弥补了单独考虑FR 和FO 时VSG 控制的不足，在频率响应速度、频率偏差、频率恢复特性和功率波动以及储能利用率方面均有积极作用。