地面沉降对燃气管道安全影响研究
张浩 吕达 陈飞 宋家才 韩金柯 张宇 孙明源 刘鹏 范佳林
1深圳市燃气集团股份有限公司
2中国石油大学(华东)储运与建筑工程学院
2020年5月,某燃气管道由于第三方施工导致管线埋土下沉,管线承受较大作用力,致使管道存在断裂风险。受影响的燃气管道位于人行道与车行道交界处,直径D508,材质为L360 钢,管道厚度7.9 mm,运行压力1.5 MPa,于2004 年投产运行。第三方施工项目开挖地基与D508 次高压燃气管线较近,最近距离约8 m(图1)。项目施工前期,为保证基坑及周边安全,施工单位对燃气管道的变形与安全状况进行了监测。监测数据显示,次高压燃气管道间接沉降超出预定报警值,最大差异沉降为0.63‰,沉降未趋于收敛稳定,存在安全隐患。为了控制管道沉降,避免管道事故的发生,施工单位进行了管底注浆加固工作,并进一步开展了管道应力检测,发现管道部分位置应力已经超过管道材料许用应力。

图1 第三方施工项目及受影响管道图Fig.1 Diagram of third party construction projects and affected pipelines
由上述案例可知,在管道运营过程中,因地下工程、降雨、基坑开挖等因素不可避免的会造成土体下沉,严重威胁管道安全,轻则导致管道变形,重则导致管道断裂。鉴于沉降引起管道事故的严重性,有必要研究沉降作用下埋地管道力学响应。
理论分析、试验模拟和数值模拟是研究沉降作用下管道力学响应、评价管道安全状态的基本方法,国内外学者已开展大量研究。在理论分析上,WINKLER[1]提出计算管道的变形受力的方法,将埋地管道看作弹性地基梁,管道周围土体看作具有一定抗压刚度系数的弹簧。日本学者高田至郎[2]通过选取沉陷区和非沉陷区的管道作为分析对象,运用弹性地基梁模型分析,得出地埋管线在塌陷情况下的简化分析公式。高惠瑛[3]等利用三次曲线模拟沉陷区管道的几何大变形,用弹性地基梁模型模拟非沉陷区的管道变形,推导出沉陷区的管道的位移及内力计算公式。邓道明[4]将灾害区外部管道看作半无限长的弹性地基梁模型,基于灾害体内外管道内力和变形的连续性,推导出管道应力和位移的计算方法。张土乔[5]等分析管道的受力特性,把埋地管道视为连续弹性地基梁,计算出管道上的最大挠度、转角和弯矩。关惠平等[6]对非沉陷区和沉陷区的管道分别构建了计算模型,得出不同塌陷区长度、不同沉降量的管道内部最大轴向应力。在试验模拟上,陈志磊[7]、张旭[8]在室内土工槽内建立试验模型,模拟了由于土体塌陷或沉降引起管线变形、影响管线正常使用这一过程。王乐[9]通过实验研究了管道在不均匀沉降作用下的力学性能,得到了不均匀沉降过程中管道的应变值和管道受力特征。在数值模拟上,RAJEEV 等[10-12]使用有限差分软件FLAC3D分析了膨胀土中管道的应力变化,同时在大型管箱中对塑料管进行了实验室实验,实验结果和模型预测之间有相当好的一致性,验证了软件分析的准确性。吴韶艳[13]等结合工程实际,比较基于有限差分软件FLAC3D的数值模拟结果和现场变形监测结果,验证了FLAC3D 模拟的可行性。赵潇[14]、王强[15]应用有限元模拟软件ABAQUS 研究了煤矿开采过程中埋地管道的变形和受力状况。
由于目前研究中,大多仅提出理论公式,并未分析公式的可靠性,也未讨论公式应用到工程实际的可行性。为此,在基于燃气管道沿线地面沉降的实际情况基础上,将力学模型计算与数值模拟方法相结合,探究土体沉降作用下管道在不同工况时的受力特征,并对已有力学模型进行修正,提出适用于不同工程实际的力学模型计算方法。
1 沉降区管道力学计算
1.1 力学模型
对于沉降区埋地管道,管道两端受到土体支撑且外侧管道受到稳定土体的约束,沉降区管道受到由于土体沉降造成的竖向载荷,根据Winkler 假设,邓道明[4]将沉降区埋地管道简化为弹性地基梁模型(图2)。
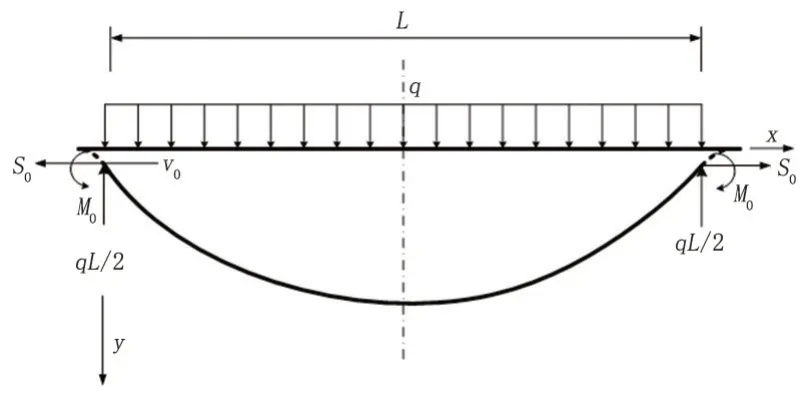
图2 管道力学模型Fig.2 Pipe mechanics model
对于沉降区内管道受力计算公式为
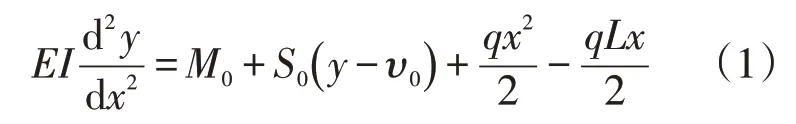
式中:E为管材的弹性模量,Pa;I为管道的截面惯性矩,m4;y为管道挠度,m;x为管道位置,m;M0为管道在x=0处截面的弯矩,N·m;υ0为管道在x=0处的挠度,m;q为作用于管道上方的均布荷载,N/m;L为管道穿越沉降区的长度,m;S0为管道的当量轴向力,N。
计算方法见式(2)。
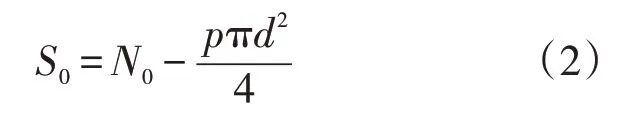
式中:N0为管道在x=0 截面的轴力,N;p为管道输送压力,Pa;d为管道内径,m。
结合边界条件求解方程,沉降区边界管道的截面弯矩计算见公式(3)。

式中:M0为沉降区边界管道的截面弯矩,N·m;k为系数;β为特征系数;D为管道外径,m。
沉降区中心管道的挠度y计算见公式(4)。
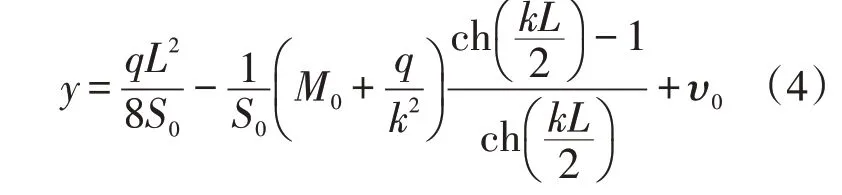
管道在滑坡段中点的截面弯矩计算见公式(5)。
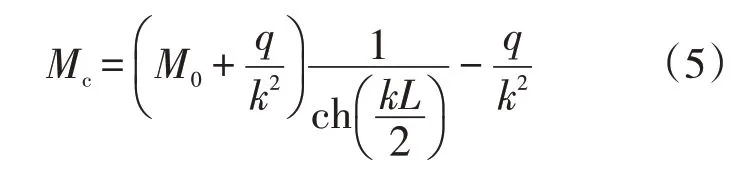
式中:Mc为滑坡段中点的截面弯矩,N·m。
其中:

式中:Cy0为管道在沉降区外稳定土层的纵向阻力系数,N/m3。
以沉降区内管道为研究对象,利用L管段轴向应变的几何非线性关系,得到管道在x=0 处的挠度,如公式(8)所示:

式中:A为管道截面积,m2;α为钢材的线膨胀系数,m/(m·℃);ΔT为管体正温差,℃;μ为泊松比,取0.3;σh为内压引起的管道环向应力,MPa。
以沉降区外稳定土层中管段为研究对象,由轴向位移的连续条件,利用半无限长埋地直管段的轴向位移一般解,确定υ0。
当(N0-Nr)γ/tf≤1 时,υ0计 算如公式(9)所示:
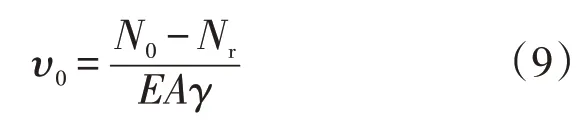
式中:γ,Nr为系数;tf为沉降区外土层的极限抗剪强度,N/m。
当(N0-Nr)γ/tf>1 时,υ0计算如公式(10)所示:
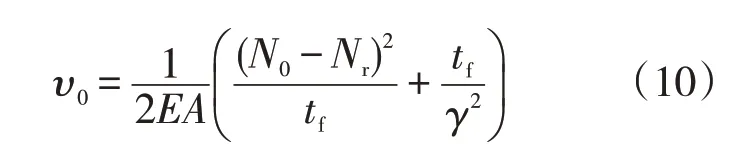
Nr的计算如公式(11)所示:
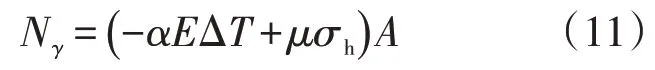
γ的计算如公式(12)所示:

式中:cx0为沉降区外土层的轴向位移阻力系数,N/m3。
1.2 沉降区管道承受载荷
上述公式计算结果的准确性很大程度上取决于输入参数的准确性。其中沉降区管道的承受荷载起到关键性作用。目前计算中对管道上方荷载通常仅考虑重力,而结合实际沉降过程中的管土相互作用分析可知,土体黏聚力和摩擦力的变化对于管土相互作用具有重要影响,据此在考虑土体、管道及管内介质重力的基础上,考虑土体摩擦力以及黏聚力的作用[16],对载荷q的计算进行修正。
自重计算如公式(13)所示:

式中:q为重力作用下管道受到的总荷载压力,N/m;q1为管道自重作用于管道上的荷载压力,N/m;q2为输送介质重力作用于管道上的荷载压力,N/m;q3为管道上方土层重力作用于管道上的荷载压力,N/m。
其中
管道自重q1计算如公式(14)所示:
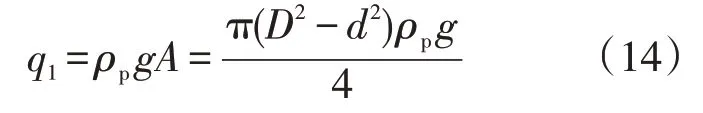
式中:ρp为管道材料的密度,kg/m3;g为重力加速度,m/s2。
输送介质重量q2计算如公式(15)所示:

管道上方土层重量q3计算如公式(16)所示:

式中:h为管道埋深,m;ρsoil为管道上方覆土密度,kg/m3。
黏聚力计算qc计算如公式(17)所示:

式中:qc为黏聚力作用力,N/m;c为土壤黏聚力,Pa。
摩擦力计算qf计算如公式(18)所示:
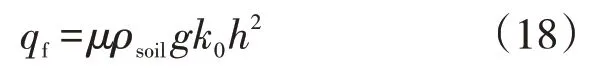
式中:qf为摩擦力作用力,N/m;k0为系数,计算如公式(19)所示:

式中:φ为土的内摩擦角(°)。
1.3 管道应力计算过程
土体沉降作用下埋地管道轴向应力计算的整个过程如图3所示。公式求解采用牛顿迭代法,首先确定计算所采用的荷载压力q;然后假定N0,逐步调整N0,使管道材料弹性变形计算过程中计算出的挠度近似相等,求出N0、M0;最终求得管道的轴向应力。计算过程复杂,可通过编制MATLAB程序实现快速计算。
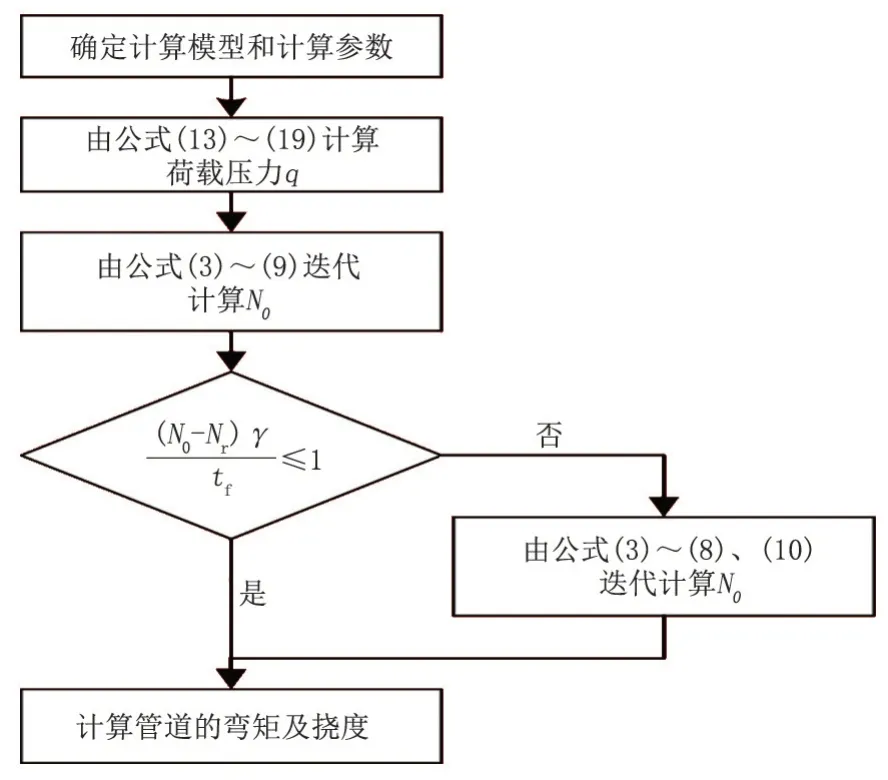
图3 迭代流程Fig.3 Iterative process
2 数值模拟
FLAC 3D软件基于有限差分拉格朗日元法,对于计算岩土工程领域常见的几何非线性大变形问题具有很大的优势。使用FLAC3D对沉降过程进行模拟,探究沉降作用下管道应力分布规律。
FLAC3D 壳型结构单元提供了壳体与网格的非线性接触,考虑了管土间的法向压缩、拉伸作用和剪切摩擦相互作用,可模拟管道与土体的接触,因此本模拟选用该结构单元建立管道模型。管材轴向拉伸曲线简化为三折线模型取值。摩尔-库伦模型适合于模拟抗压强度和抗拉强度不同的岩石以及砂土粒状材料,并且用常规实验可以很容易获得摩尔-库伦模型的各项参数,使用起来简单便捷,被广泛应用于岩土工程的数值分析[17],因此本模拟采用摩尔-库伦模型建立土体模型。
根据王乐[9]的研究,当采用固定边界模型时,管道相当于具有固定边界的简支梁,为了避免出现边界效应,整个沉降模型长度应至少为管道直径的60倍,即Ltotal=L+60D。式中Ltotal为模型的轴向长度,m;L为沉降区长度,m;D为管道的直径,m。结合张杰[18]的研究,模型的横向和纵向尺寸可以取为10 倍管径,综上确定沉降模型规模按()L+60D×13D×10D(长×宽×高)建立。
土体选用六面体网格划分,分别对沉降区、沉降区与非沉降区交界处附近及管道周围的网格进行加密处理,对土体的非沉降区下表面及各侧面分别施加法向约束,对管道两端施加全约束。D508 管道由4 960 个结构单元组成,土体由37 448 个实体单元组成(图4);D813管道由5 280个结构单元组成,土体由49 764个实体单元组成。管道及沉降土体的性质参数见表1 和表2,其中管道参数根据某燃气公司实际管道选取,土体参数根据易发生沉降地区的土体实测得到。

表1 实验管道参数Tab.1 Experimental pipeline parameters

表2 沉降土体基本参数Tab.2 Basic parameters of settlement soil
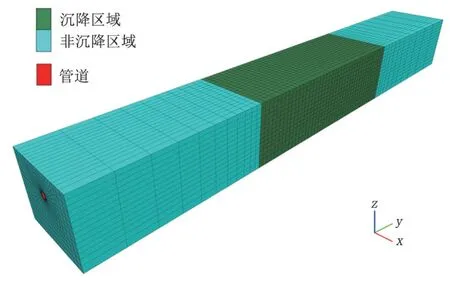
图4 FLAC 3D模型图Fig.4 Figure of FLAC 3D model
数值模拟整体分为两个步骤:①对模型施加重力以实现地应力平衡;②沉降区域底面施加竖向沉降位移。为了验证修正后的力学模型计算方法的可行性,分别讨论了不同沉降范围、土体黏聚力及管道壁厚下管道的受力特征,分析了力学模型计算结果与模拟结果间的误差。
3 模拟结果分析
3.1 沉降范围对管道的影响
不同的管道沉降灾害可能出现不同的沉降范围,图5 为不同沉降范围下管道轴向应力分布图。由图5可知,沉降范围的变化对于管道受力具有显著影响。沉降范围为10 m 时,D813 管道并未发生塑性变形,随着沉降范围增加,管道中部受力达到屈服极限,管道进入塑性变形阶段。相同沉降范围下,D813 管道的中间塑性变形段管道长度<D508管道,这表明管道的管径越大,管道中部的应力越小;若管道中部应力达到管材屈服应力,则管道中间部位达到屈服应力后发生塑性变形的管段长度减小。对于D508 的管道,在沉降范围为30 m 时,沉降中心管道应力明显降低,这表明沉降范围的增加并不能无限增加管道中间塑性变形段的长度。由此可见,在管道沉降灾害中,沉降边界附近的管道受到破坏的概率最大,需要重点关注。
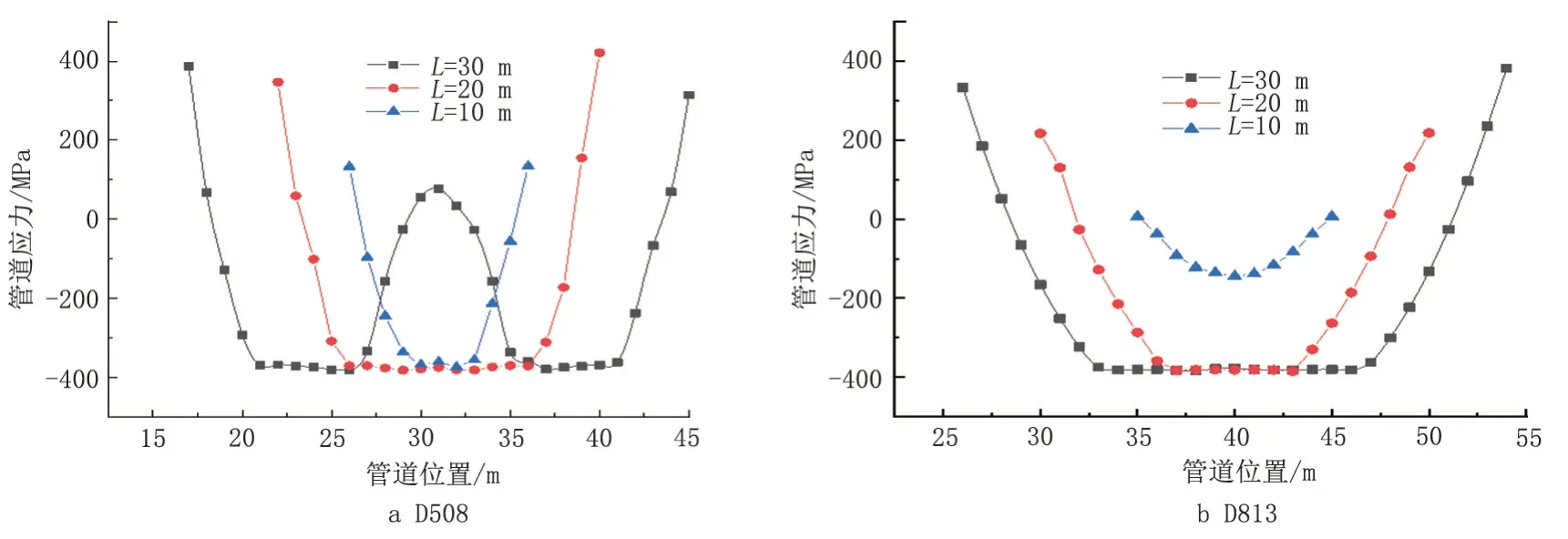
图5 不同沉降范围下不同管径管道的轴向应力分布Fig.5 Axial stress distribution of different pipeline diameters under different settlement ranges
3.2 土体黏聚力对管道的影响
黏聚力是表征土体性质的重要指标之一,不同类型的土体具有不同的黏聚力,纯砂土黏聚力几乎为0,而黏土黏聚力往往超过10 000 Pa,根据模拟中的黏聚力5 660 Pa,取1/2和2倍数关系,模拟得到不同土体黏聚力下的管道轴向应力分布如图6所示。对于D508 管道,随着黏聚力的增加,管道中部塑性变形管道范围略有增加,且管道中部轴向应力出现略为减小的趋势;对于D813 管道,管道中部塑性变形管道范围同样略有增加,但塑性变形外管道轴向应力变化更加剧烈。研究结果表明,土体黏聚力变化对管道受力的影响较小,随着黏聚力增加,沉降区中间管道发生塑性变形的范围略有增加。
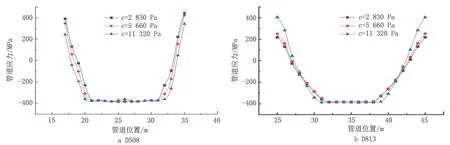
图6 不同土体黏聚力下不同管径管道的轴向应力分布Fig.6 Axial stress distribution of different pipeline diameters under different soil cohesion
3.3 管道壁厚对管道的影响
不同沉降灾害中管道的壁厚存在差异,上述沉降过程中,D508 管道的壁厚为7.9 mm,D813 管道的壁厚为11.9 mm,根据GBT 21835《焊接钢管尺寸及单位长度重量》,对D508 管道另选6.3 mm 和8.8 mm壁厚,对D813管道另选10 mm和14.2 mm壁厚进行研究,图7为不同的壁厚下的管道轴向应力分布图。由图7 可知,壁厚对管道受力的影响很小,随着壁厚增加,管道的中间塑性区范围略有降低。
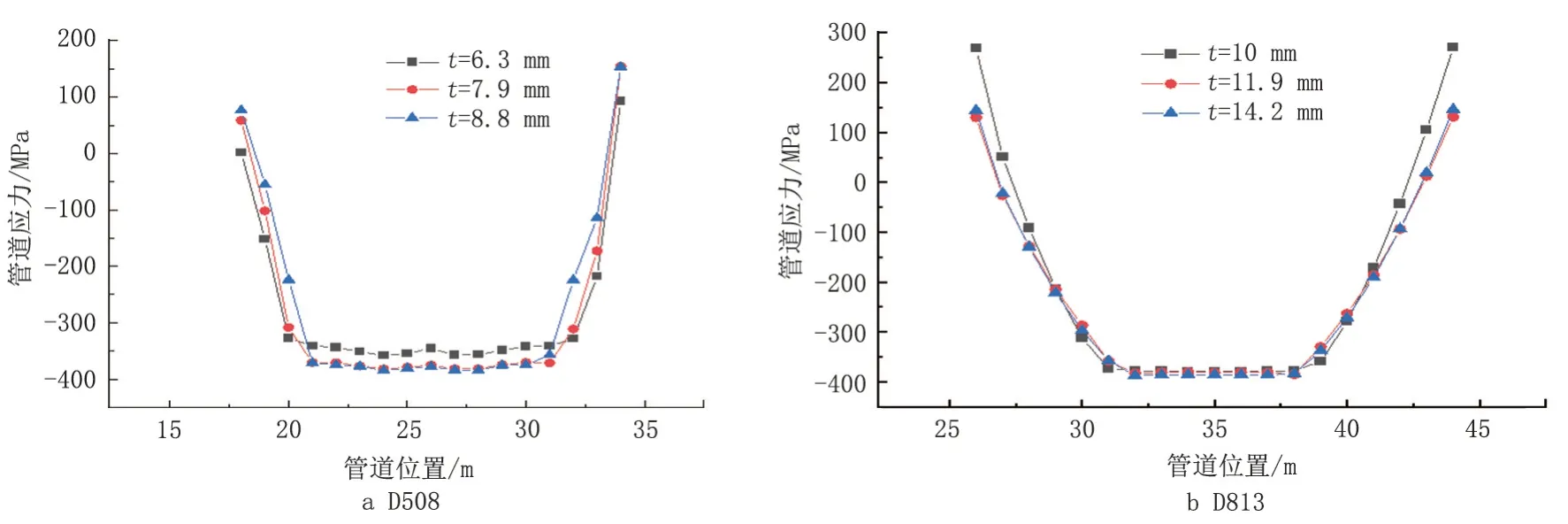
图7 不同管道壁厚下不同管径管道的轴向应力分布Fig.7 Axial stress distribution of different pipeline diameters under different pipeline wall thicknesses
4 模拟与计算结果的对比
4.1 不同沉降范围下的对比
4.1.1 D508管道
图8 为不同沉降范围下D508 管道力学模型计算得到的管道应力与模拟所得数据的对比结果。沉降范围对结果影响较大,沉降区长度为10 m 时,D508 管道的力学模型计算所得应力曲线与模拟所得应力曲线贴合度较好;沉降区长度为20 m、30 m时,D508 管道中间部位发生塑性变形,管道中部应力不再继续增加,而力学计算按照管道弹性开展计算,故力学模型计算所得最大应力与模拟所得应力在此段误差较大,力学模型计算所得应力明显偏大。因此,力学模型计算适用于弹性变形区应力大小计算,对于超过屈服强度的部分建议在该区段采取基于应变的管道破坏准则计算。
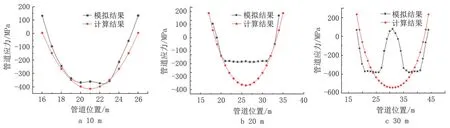
图8 D508管道不同沉降范围下应力模拟结果与理论计算结果对比Fig.8 Comparison between stress simulation results and theoretical calculation results under different settlement ranges of D508 pipeline
4.1.2 D813管道
图9 为不同沉降范围下D813 管道力学模型计算得到的管道应力与模拟所得数据的对比结果。沉降区长度较小时,D813 管道的力学模型计算所得应力曲线与模拟所得应力曲线贴合度较好;沉降区长度较大时,D813 管道中间出现塑性区,导致力学模型计算结果在此段与模拟结果出现差别,且随着沉降区长度的增大,管道塑性区内的计算结果误差不断增大。
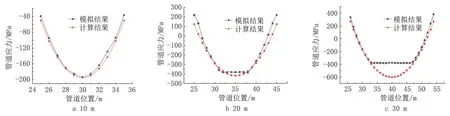
图9 D813管道不同沉降范围下应力模拟结果与理论计算结果对比Fig.9 Comparison between stress simulation results and theoretical calculation results under different settlement ranges of D813 pipeline
4.2 不同土体黏聚力下的对比
4.2.1 D508管道
图10 为不同土体黏聚力下D508 管道力学模型计算得到的管道应力与模拟所得数据的对比图。虽然模拟结果受黏聚力的影响较小,但是力学模型计算结果受影响较大。随着黏聚力增大,力学模型计算所得最大应力不断增加,模拟所得应力基本不变,因此对于该直径的管道,力学模型计算结果与模拟结果在塑性段的误差不断增大。
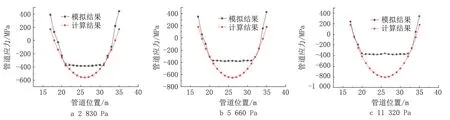
图10 D508管道不同土体黏聚力下应力模拟结果与理论计算结果对比Fig.10 Comparison between stress simulation results and theoretical calculation results under different soil cohesion of D508 pipeline
4.2.2 D813管道
图11 为不同土体黏聚力下D813 管道力学模型计算得到的管道应力与模拟所得数据的对比图。随着黏聚力增大,力学模型计算结果与模拟结果贴合度不断增加,但是当黏聚力增大至11 320 Pa 时,力学模型计算结果显著大于模拟结果,呈现出过于保守的情况,已无法准确体现模拟所得管道应力分布。在各类土体中,黏土黏聚力很大,由此可知,管道处于黏土环境下,对于该直径的管道,采用上述计算方法得到的管道应力十分保守。

图11 D813管道不同土体黏聚力下应力模拟结果与理论计算结果对比Fig.11 Comparison between stress simulation results and theoretical calculation results under different soil cohesion of D813 pipeline
4.3 不同管道壁厚下的对比
4.3.1 D508管道
图12 为不同壁厚下D508 管道力学模型计算得到的管道应力与模拟所得数据的对比图。管道应力计算结果受壁厚的影响很小,不同壁厚下,力学模型计算所得结果与模拟结果的误差基本不变,但管道塑性变形区受壁厚的影响而变化,壁厚越大,模拟所得管道塑性区范围越小。
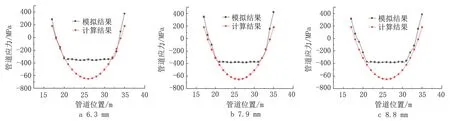
图12 D508管道不同管道壁厚下应力模拟结果与理论计算结果对比Fig.12 Comparison between stress simulation results and theoretical calculation results under different pipeline wall thicknesses of D508
4.3.2 D813管道
图13为不同壁厚下D813 管道力学模型计算得到的管道应力与模拟所得数据的对比图。不同壁厚下,力学模型计算所得结果曲线与模拟结果曲线较为贴合,随着壁厚越大,贴合度不断增加。

图13 D813管道不同管道壁厚下应力模拟结果与理论计算结果对比Fig.13 Comparison between stress simulation results and theoretical calculation results under different pipeline wall thicknesses of D813
5 结论
基于燃气公司实际管道情况,通过数值模拟分析了土体沉降作用下管道在不同工况时的受力特征,结合修正后的力学模型计算方法,讨论了计算结果与模拟结果间的误差,得到如下结论:
(1)沉降范围对管道的受力结果影响较大。沉降范围增加,管道中部达到屈服应力后发生塑性变形的管段明显增加。但沉降范围的增加并不能无限增加管道中间塑性变形段的长度,沉降范围过大时管道中间部位不会发生塑性变形,而沉降边界附近的管道始终发生塑性变形。
(2)土体黏聚力变化对沉降灾害下管道受力影响较小,而管道壁厚的变化几乎对其无影响。
(3)修正后的力学模型计算结果在管道受力未超过屈服强度时与数值模拟结果具有较好的吻合度,超过管道屈服应力时其计算结果不再可靠,需采取基于应变的管道破坏准则进行计算。

