S32205不锈钢弯管在气固两相流下的冲蚀模拟研究*

李良均 刘书文 程文钦 蔡从德 李科 王明春

1四川科宏石油天然气工程有限公司

2西南石油大学

3中国石油西南油气田公司长宁页岩气公司

冲蚀是流体或流体中所含颗粒与固体表面发生冲撞而产生的一种现象，这种现象在众多工业领域中极为常见，也是页岩气开采与输送的主要威胁因素[1]。相较于常规天然气，页岩气的储层特性有所不同，进行页岩气开采之前首先要进行压裂，这导致地层中部分压裂产生的砂粒在开采时会进入井筒，且进一步沿着井筒进入到输送管线。如威204 井区中的H10 平台在页岩气排采阶段会出现产气量大、出砂较多的现象。在开始生产阶段，需要向地层注入大量陶粒和石英砂等固体颗粒，而这些颗粒将随着页岩气返排至地面集输系统，与平台井站集气管道发生碰撞，产生严重的冲刷腐蚀。弯头使管道中气体的流向发生突变，致使砂粒与壁面发生较强碰撞，进而使弯管成为页岩气集输管道易被破坏的薄弱环节。

管道的冲蚀涉及气流的流场特征，因此基于固体颗粒的运动规律预测冲蚀速率和冲蚀分布，采取正确可行的对策，对页岩气田的安全运行具有重要意义。许多学者通过实验研究了颗粒对管道的冲蚀规律[2-3]，但弯管冲蚀实验会浪费大量的时间及经济成本，并且测试设备通常会对实际的流场有一定程度的干扰。因此，采用合理的数值模拟方法是一种更为便利的研究途径，不仅能够直观、清晰地理解流体动力学问题，还能节省时间及经济成本。

CHEN X等人借助CFD冲蚀预测模型对堵塞三通和弯头在气固两相流条件下的相对侵蚀程度进行了研究[4]。李沧等人使用E/CRC 冲蚀磨损模型，对90°集输管道弯管进行气固两相流的模拟计算，从气体的速度、固体杂质微粒的粒径及固体杂质微粒的质量流率等因素讨论弯管的冲蚀磨损情况，研究结果表明90°弯管的冲蚀率与因素影响基本呈正相关[5]。ZENG D等人基于CFD-DEM 模型，建立了考虑气固、颗粒和颗粒壁相互作用的气固两相流冲蚀预测模型[6]，结果表明V 形冲蚀痕迹是由二次冲击引起。WANG K 建立了考虑颗粒-流体相互作用的输油管道弯头固体颗粒冲蚀预测数学模型，结果表明腐蚀主要发生在弯管出口附近，尤其是下游直管的侧壁和弯曲段的圆顶处[7]。

为探寻控制页岩气集输管道冲蚀的有效手段，以耐蚀性较好的S32205 双相不锈钢为研究对象，采用CFD 模型结合DPM 数值方法，研究90°弯管在气固两相流作用下的冲蚀情况。为了获得更具参考价值的结果，模拟实验条件选取川南页岩气田实际工作环境，通过砂配比、流速及压力等影响因素研究冲蚀磨损规律。

1 数学模型

1.1 流体控制方程

流体在集输管线中的流动要遵循基本的物理守恒定律[8]。气固两相流的瞬时体积平均守恒方程组可以依据牛顿第二定律和守恒定律中的质量守恒定律得到，它的通用形式如下：

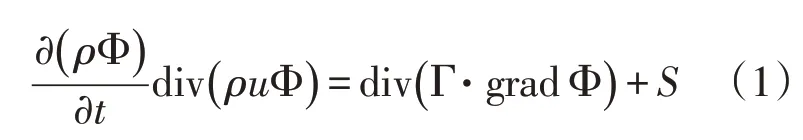
式中：ρ为密度，kg/m3；t为时间，s；u为流动速率，m/s，u=ui+uj（i，j为坐标轴x、y方向向量）；Φ 为通用变量；为瞬态项；div(ρuΦ)为对流项；div(Γ·grad Φ)为扩散项；S为源项。对于特定的方程，Φ、Г、S分别对应特定的形式。

1.2 湍流模型

湍流是流体在流动过程中呈现的一种状态，其特点是各流体在流动时始终是不稳定、不规则的，且在湍流层中各点的压力和速度都在不断变化。目前还没有一种模拟方法能够完全真实反应流动过程中的湍流情况，因此对于不同情况应选择与其流动特点相近的湍流模型。雷诺数是区分湍流和层流的重要参数，当雷诺数大于2300 时为湍流，反之则为层流。其公式为：

式中：D为直径，m；u为流体的运动速度，m/s；ρ为流体介质的密度，kg/m3；μ为流体介质的动力黏度，Pa·s。

Fluent 软件中的湍流模型较全面，主要包括RSM 模型[9]、Spalart -Allmaras 模型、LES 模型[10-11]、k-ω模型、k-ε模型等六种湍流模型。近年来，学者们对各种模型不断探索与延伸，发展形成了标准k-ω模型、Realizablek-ω模型和RNGk-ω模型；k-ω模型发展形成了标准k-ω模型[12]、SSTk-ω模型两种模型。在选择模型时应结合模型的限制条件和使用范围，并从流体性质、模拟精度、计算机能力和模拟时长等因素综合考虑。

k-ω模型由两部分组成，方程k是一个代表湍流动能的精确方程，方程ε是代表耗损率的经验方程。其中标准k-ω模型是一种较为简化的模型，忽略流体分子之间的黏性，将流场理想为完全在湍流的运动状态，这使得在出现漩涡的情况下模拟结果不太准确。YAKHOT 和ORZAG 等将标准k-ω模型的一些参数改进后提出了RNGk-ω模型，该模型在湍流产生漩涡时能够有效地降低涡流产生的影响，因此与另外两个k-ω模型相比，该模型的经验方程ε的结果更可靠[13]。除此之外，在处理Prandtl 数时，RNGk-ω模型并不需要用户提供相关的数值，而是通过解析公式来实现，这能够更好地符合不同流体的运动状态。综合上述分析，RNGk-ε模型的求解结果更加精确，相应的运输方程为[14]：

湍流+动能k方程：

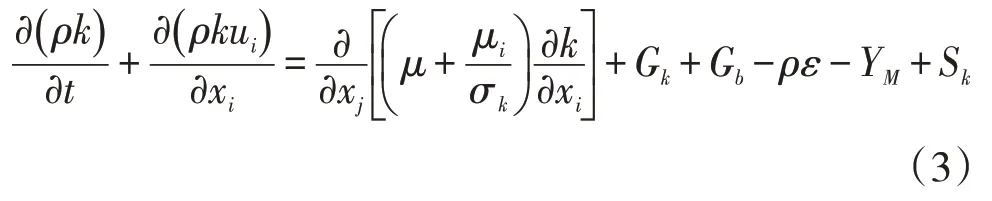
耗散率ε方程：

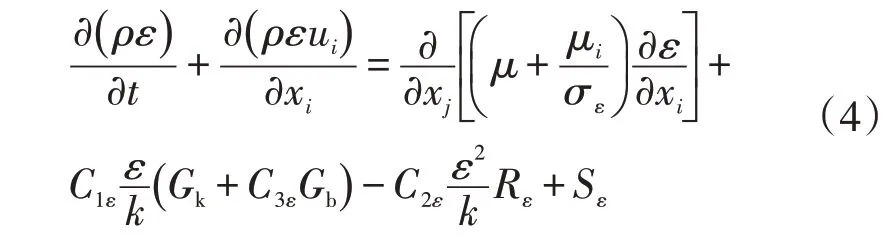
式中：t为时间，s；k为湍动能，J；ρ为流体密度，kg/m3；Gk为平均速度梯度；ε为湍流耗散率，J/s；Gb为浮力影响引起的湍动能产生项；Sk、Sε为用户定义 项；C1ε、C2ε、C3ε为经验常数；σk为湍动能对应的普朗特数；σε为湍动耗散率对应的普朗特数。上述常数在Fluent 中默认值为：σε=1.3，σk=1.0，C1ε=1.44，C2ε=1.92，C3ε=0.09。

本次研究是对页岩气集输管道中弯管部件进行冲蚀，其流动状态为湍流，并且选取的管段较短，将气体介质看作是不可压缩流体能够有效减少计算量，再加上考虑计算机的计算效率、计算精度等因素，因此选择RNGk-ε模型进行模拟较为适宜[15]。

1.3 冲蚀模型

冲蚀模型主要包括E/CRC 冲蚀模型[16]、Oka 模型[17-18]及Generic 模型[19]，其中Oka 模型是由广岛大学的Oka等人结合大量实验数据及前人经验后提出的，其方程为：

式中：V′为参考碰撞速度，m/s；；vp为冲击速度，m/s；Hv为靶材的维氏硬度值，GPa；ρω为管材密度，kg/m3；d′为参考颗粒粒径，μm；d为颗粒粒径，μm；θ为冲击角度，°；n1和n2由材料硬度或其他冲击条件决定，K、k1和k2是由颗粒性质决定的常数，k3是材料硬度和颗粒性质的函数。

该模型所涉及的因素比较多，从颗粒和靶材的角度进行了考虑，其中颗粒方面主要涉及到颗粒入射角度、速度及颗粒直径等因素，靶材方面考虑的因素主要包括靶材密度、硬度等，因此本次实验选择Oka模型能够使计算结果更加精确。

2 数值模拟

2.1 模型建立及网格划分

（1）模型建立。在本次实验中，使用Fluent 19.0 模拟了90°弯头在气固两相条件下的冲蚀过程。管道的管径根据现场实际输送管道设置，即管径D=257 mm，弯径比R/D=1.5，在弯头入口处设置直管段，令入口段直管长度L1=8D，充分展开流动状态；弯头出口处的直管段，出口段直管长度L2=4D，既能保证水流充分发展，防止回流，又能观察颗粒在弯头处碰撞后的运动轨迹。弯管模型见图1。

图1 90°弯管模型Fig.1 90°elbow model

（2）网格划分。网格划分是进行CFD 模拟分析之前一个十分重要的步骤。从计算机的计算精度与计算量角度考虑，使用ICEM 软件对弯管进行结构化网格的设计。流体在直管段时受到周围介质的影响较小，湍流强度的变化也较小，因此在网格划分时，将直管段网格划分较为稀疏，可在不影响实验结果的前提下减少计算机的载荷。而在弯头部分，流体参数变化较大，此段网格划分时进行必要的细化，这能够使模拟结果更加可靠；同时增加边界层网格层数来提高边界层的计算精度。根据上述网格划分规则，弯管最终划分的网格数为1887117（图2）。

图2 弯管网格Fig.2 Grids of elbow

一般来说，网格质量大于0.3 即可进行模拟计算。从图3 可知，本次弯管划分网格质量的在0.965～1.0 之间的超过50%，质量在0.9 以上的约91%以上，这说明该弯管的划分网格完全能够满足计算需要。

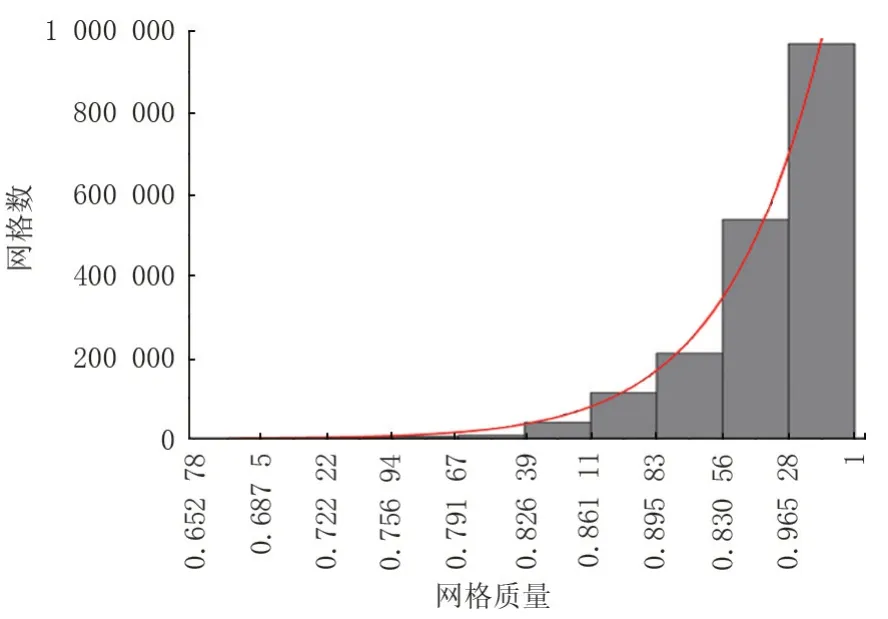
图3 弯管划分网格质量Fig.3 Quality of elbow gird division

2.2 实验参数选取

在本次实验中选取S32205 双相不锈钢作为管道材料进行模拟，其性能参数如表1、表2所示。

表1 S32205双相不锈钢力学性能Tab.1 Mechanical properties of S32205 duplex stainless steel

表2 S32205双相不锈钢物理性能Tab.2 Physical properties of S32205 duplex stainless steel

集输管道的冲蚀率受到众多因素的影响，为了使模拟结果更加接近现场实际冲蚀情况，实验参数均按照川南页岩气工作条件选取（表3）。

表3 数值模拟实验参数选取Tab.3 Parameter selection of numerical simulation experiment

考虑到计算的有效性及真实性，对计算的边界条件进行如下设定：管道内流体为页岩气，其主要成分为甲烷（CH4），因此模拟过程中以甲烷代替页岩气进行模拟；由于管道中气体流速不高，将其看作不可压缩流体对模拟结果的影响不大。

由于页岩气的流速通常在现场可以测得，因此在模拟计算时将速度作为流体的入口边界条件，假定流体各点的初始速度相同，并以湍流的状态平行于直管方向流入。将压力作为出口处边界条件，压力在出口处均匀分布，方向垂直于出口截面。根据表3参数对速度及压力值进行设置，此外还需要对进出口的湍流参数进行设定：将截面水力直径设为DH=D=257 mm，湍流强度设为I=4%；将离散相模型中颗粒射流源设为面源，即颗粒在入口截面均匀分布，且速度与流体相同。为了探究颗粒对管壁的冲蚀率，将管壁壁面设为非滑移边界，颗粒与壁面碰撞法向量的反弹阻力功率系数en和切向量的反弹功率系数et如式（7）、式（8）所示：

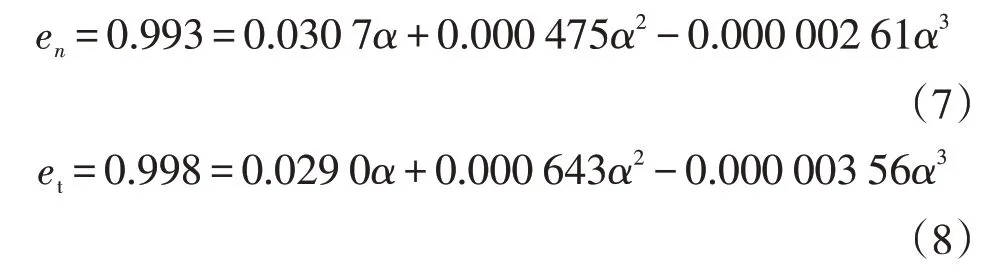
为有效求解模型，Fluent 软件中求解器设置如表4所示。

表4 流动条件及求解设置Tab.4 Flow conditions and solution settings

根据Fluent 的适用条件和气固两相流的特点，本次实验做出如下合理假设：

（1）所述固体颗粒均匀地从弯头入口处射入，视为表面射流源；

（2）管道内颗粒碰撞后不发生破碎等现象，在出口流动中仍为完整颗粒；

（3）墙体材料各处的力学性能不存在差异，各处的物理参数恒定；

（4）管道内不发生固体颗粒沉积、粘附现象。

3 结果与讨论

3.1 正交实验分析

本实验主要研究在不同砂配比、不同流速及不同压力情况下弯管的冲蚀速率。表5 及图4 是对上述因素进行正交实验后的冲蚀率结果。结果表明，在本次设置参数条件下，S32205 不锈钢的最大冲蚀率为5.30×10-3mm/a，最小冲蚀率为3.87×10-4mm/a。

表5 不同条件下S32205不锈钢冲蚀率Tab.5 Erosion rate of S32205 stainless steel under different conditions

图4 不同条件下S32205不锈钢冲蚀率曲线Fig.4 Erosion rate curve of S32205 stainless steel under different conditions

为探究各因素对冲蚀率的影响大小，对上述结果进行极差分析，结果如图5、表6所示。

由图5、表6 可知，在本次实验选取参数中，从3个因素来看，结合R值（因素极差值）的大小对比可知：因子B（流速）是对冲蚀率影响最大的因素，其次是因子A（砂配比），最后是因子C（压力）。因而3 个因素按对管壁冲蚀率的影响大小排序为：因子B＞因子A＞因子C。具体结合各因子的最佳水平可知：多数钢材在因子A以第4个水平即石英砂/陶粒配比为20/80时冲蚀最严重；因子B以第1 个水平即10 m/s 时冲蚀最严重；因子C 以第1个水平即5.5MPa冲蚀最严重。

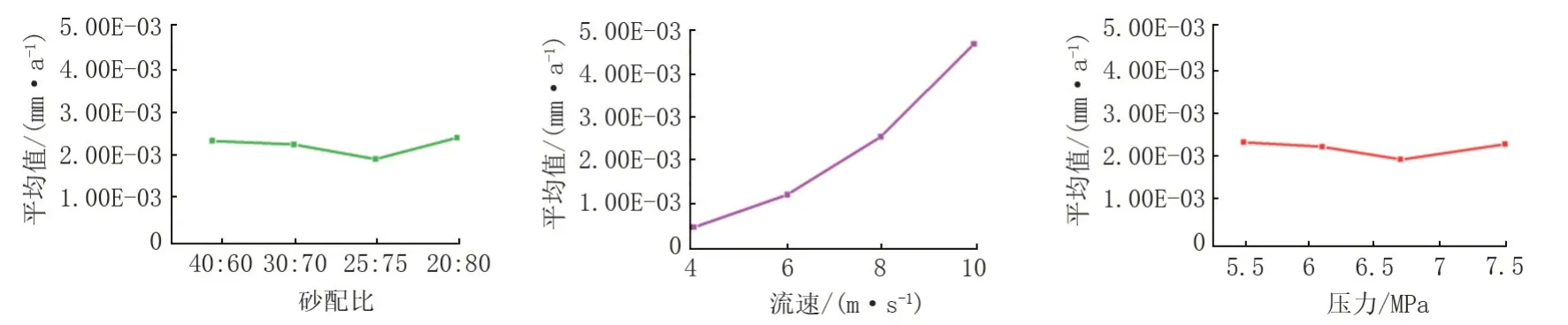
图5 模拟弯管冲蚀率极差分析曲线Fig.5 Curve of simulated erosion rate range analysis of elbow

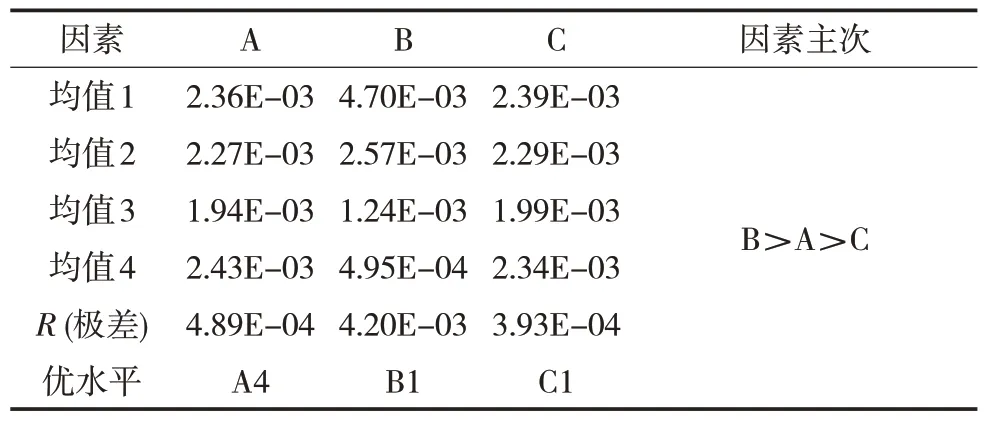
表6 90°弯管冲蚀率极差分析表Tab.6 Range analysis table of erosion rate of 90°elbow

综合上述分析可知：对冲蚀率影响最大的因子为流速。冲蚀最严重的条件为“石英砂/陶粒配比20/80，流速10 m/s，压力5.5 MPa”。

3.2 弯头流场分析

为了深入分析弯头流场，以条件“石英砂/陶粒比例20/80，流速10 m/s，压力5.5 MPa”为例进行局部分析。

图6是弯头中的压力分布，可以看出：由于直管出口处边界条件为压力出口，整个弯管的压力值在5.5 MPa 左右；弯头外侧的压力相对较高，且压力随径向逐渐降低。从不同截面压力图可以看出，角度在0°到45°区间时，随着角度逐渐增加，弯头内外压力差异逐渐增大；角度在45°到90°区间时，随着角度逐渐增加，弯头内外压力差异逐渐减小。

图6 弯头压力分布图及不同角度压力截面图Fig.6 Pressure distribution diagram of elbow and cross section diagram of pressure at different angles

图7为不同角度截面流速，可以看出：弯头内侧流速均高于弯头外侧流速，且轴向角由0°增加到45°时，弯头外侧的流速在逐渐减小，弯头内侧的流速在逐渐增大；轴向角由45°增加到90°时，弯头外侧流速在逐渐增大，弯头内侧流速在逐渐减小。

图8为冲蚀轨迹及冲蚀云图，可以看出，颗粒轨迹在入口直管段基本呈直线，在弯头段颗粒与管壁发生碰撞，轨迹发生变化。在这个过程中与壁面发生碰撞的颗粒动能转化为冲击能，因而速率变化较大，而弯管外壁颗粒未直接与壁面发生碰撞，其动能损失较少，速率相较于弯管外壁动能较大。该结果与图7结果相吻合。

图7 不同角度截面流速矢量图Fig.7 Vector diagram of cross section velocity at different angles

图9为弯管截面位置及各截面最大冲蚀率，可以看出冲蚀最严重位置在靠近弯管出口位置，且随着弯管截面角度的增大，即从图9a中0°到90°位置，冲蚀率在逐渐增加。结合图8颗粒轨迹推测，是由于弯道外侧颗粒与壁面发生碰撞之后受到弯道内侧颗粒的的冲击力及重力方向影响，颗粒对壁面发生二次冲击，使得冲蚀最严重位置位于靠近弯道出口位置。

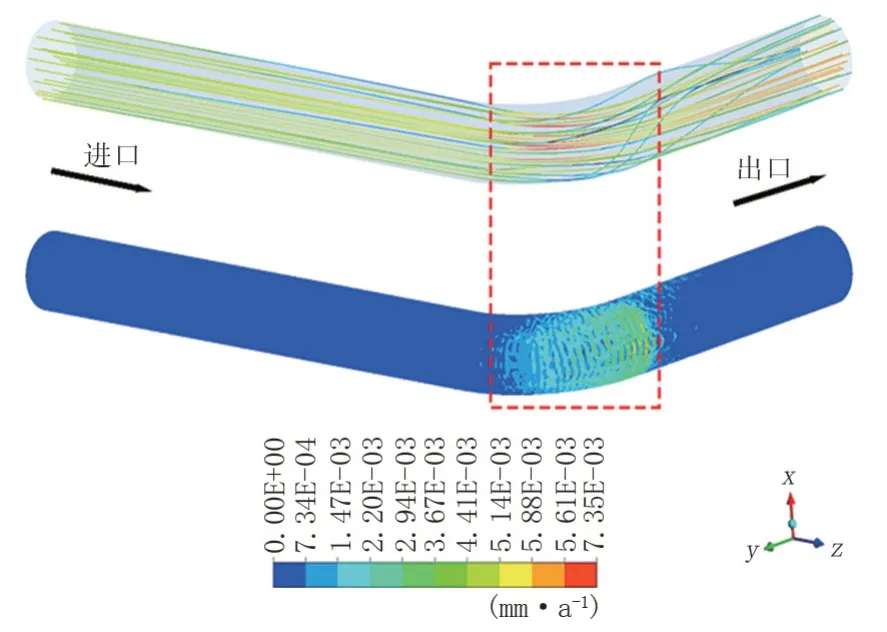
图8 冲蚀轨迹及冲蚀云图Fig.8 Erosion track and erosion cloud map

图9 弯管截面冲蚀率Fig.9 Erosion rate of elbow section

4 结论

本次实验采用数值模拟方法研究了S32205 双相不锈钢制作的页岩气集输管线中90°弯管在气固两相流条件下的冲蚀，选用RNGk-ε模型离散相模型及Oka冲蚀模型相耦合。结果表明：

（1）在选定实验参数下，S32205 不锈钢的最大冲蚀率为5.30×10-3mm/a，最小冲蚀率为3.87×10-4mm/a。

（2）在选定实验参数中，3 个因素按对管壁冲蚀率的影响大小排序为：因子B（流速）＞因子A（砂配比）＞因子C（压力）。

（3）颗粒运动轨迹表明，颗粒在入口直管段基本呈直线运动，当颗粒与弯头发生撞击后运动轨迹发生变化。

（4）根据弯头压力及流速可知，压力在弯头外侧升高而流速降低，弯头内侧压力较低流速较高。

（5）冲蚀最严重的位置处于弯头出口位置，因此在弯头处应作出一定的预防措施。