步退应力加速可靠性试验方法及应用

周天朋，王新，祝济之，刘忠平

（1.天津航天瑞莱科技有限公司，天津 300462； 2.北京强度环境研究所，北京 100076）

引言

长期以来高可靠长寿命评估都是可靠性工程领域面临的一个技术难题。长寿命评估手段的不足对产品的研制和使用造成不利影响，其一，是新研产品的寿命指标无法在研制阶段进行充分验证，可能造成严重的寿命隐患；其二，使得某些产品提前报废，不能充分发挥产品的寿命潜力，造成巨大资源浪费。加速可靠性（寿命）试验技术的应用成为高可靠长寿命产品研制的必要手段。加速可靠性试验是在失效机理不变的条件下，通过加大试验应力水平来减少试验时间的一种可靠性评估试验技术[1]。加速可靠性试验技术适用于可靠性水平高，可靠性时间周期长的产品，此外也有利于减少产品研制周期和费用。目前已经在高端装备的机械、电子、机电、材料等诸多领域得到了广泛应用[2,3]。

按照应力加载的类型，加速可靠性试验可分为恒定应力试验、步进应力试验、序进应力试验和步退应力试验四种类型。通过理论分析和数值仿真，已经证实步退应力试验在四种加速可靠性试验方式中试验效率最高，试验时间最短[1,4]。

本文介绍步退应力加速可靠性试验的工程应用方法，给出产品可靠性服从指数分布或威布尔分布时，其加速可靠性试验的数学模型，模型参数的约束关系，以及加速因子计算公式。本文提出一种可以满足给定置信水平和特征寿命精度的步退应力加速可靠性试验方案，以及加速可靠性模型参数的计算方法，并给出试验案例，说明求解过程。

1 加速寿命试验物理模型

加速寿命试验是利用高应力下的寿命特征去外推正常应力水平下的寿命特征。需要建立寿命特征与应力水平之间的关系，即加速模型。在加速模型中最常用的是阿伦尼斯模型和逆幂率模型。

1.1 阿伦尼斯模型[5]

阿伦尼斯模型是基于温度应力加速的寿命模型：

式中：

L—某寿命特征；

A—常数；

Ea—活化能；

k—玻尔兹曼常数；

T—绝对温度。

温度T2相对于温度T1下产品寿命的加速因子：

阿伦尼斯模型广泛应用电子产品加速寿命试验和加速贮存寿命试验中。

1.2 逆幂率模型[6]

产品经常遇到的应力还有机械应力和电应力，大量试验数据表明，产品在机械应力与电应力作用下的寿命特征与应力的关系符合逆幂率模型：

式中：

L—某寿命特征；

A、n—常数；

S—应力水平。

应力S2相对于应力S1下产品寿命的加速因子：

2 加速可靠性试验的加速因子

在加速寿命试验模型的基础上，考虑寿命的可靠性分布特征，即形成加速可靠性试验模型。加速可靠性试验是失效过程的加速，受试产品在短时间高应力作用下，表现的失效特性与产品在长时间低应力作用下失效特性一致。失效特性一致性具体表现为[7]：

1）失效过程的规律一致性：指产品寿命与应力之间存在同一个确定的函数模型。只是不同应力水平下函数的参数不同。

2）失效机理的一致性：指失效模式不变。对于威布尔分布，形状参数表征了威布尔分布的失效机理[8]，形状参数不变是威布尔分布加速寿命试验失效机理一致的充要条件。对于指数分布来说，失效机理一致性的充要条件就是在不同应力下产品失效分布均符合指数分布。

加速因子定义：若产品在应力水平S1和S2分别作用时间t1与t2的累积失效概率相同，即F1(t1)=F2(t2)，则应力S2相对于应力S1的加速可靠性试验的加速因子为：

指数分布的累积失效概率表达式为：

式中：

F(t)—累积不可靠度；

λ—失效率（同一应力下λ为常数）；

t—时间。

两种应力条件下，指数分布的加速因子：

威布尔分布的累积失效概率表达式为：

式中：

F(t)—累积不可靠度；

η—尺度参数（特征寿命，同一应力下为常数）；

m—形状参数（不同应力下均为常数）；

t—时间。

两种应力条件下，威布尔分布的加速因子：

3 步退应力加速可靠性试验方案及求解

因为试验样本和经费预算，步退应力加速可靠性试验方案最少可以设置2个应力梯度，第1阶段施加的应力通常为产品的极限应力，第2阶段应力比第1阶段应力降低，但也应远大于正常工作应力。

3.1 指数分布试验方案及求解

对于指数分布，需要求解故障率或平均无故障工作时间（MTBF）。使用定数截尾的方案，MTBF单侧置信下限θL为[9]：

式中：

n—样本数；

r—失效数；

γ—置信水平；

χ2—卡方分布；

Ti—第i个样本失效时间。

置信水平0.8和0.9，失效数r=1-5时，分布值见表1。

表1 χ2分布值

以2个样本为例，在第一组S2应力下，t1时间发生1次失效，第一组试验结束。

剩余1个样本转入第二组S1应力下进行试验，t2时间发生第2次失效，试验结束。

选择置信水平0.8，根据式（10）可以评估得到S2应力下MTBF置信下限：

根据S1应力下的试验数据，可以评估得到S1应力下MTBF置信下限：

进一步可以得到S2应力相对于S1应力下的加速系数：

若产品施加的是温度应力，加速寿命服从阿伦尼斯模型，令T1=S1，T2=S2，将加速因子α2,1和温度应力值带入式（2），即可计算得到活化能Ea。

根据式（2），即可计算温度应力T2相对于工作温度应力T0的加速系数α2,0，进而可以得到工作温度应力T0下的MTBF单侧置信下限θLT0。

3.2 威布尔分布试验方案及求解

根据文献[10]，产品寿命服从威布尔分布，可靠性试验时最少试件数量要求见表2。

表2 威布尔分布可靠性试验最少试件数

形状参数m越小需要试验件数量越多，当形状参数m=2.2，特征寿命精度10 %，置信水平0.8时，需要试件数12。

若试验结束时产品有3/4发生失效，试验总样本选24件，在第一组应力S2下需要12件样品发生失效，即可拟合出威布尔可靠性分布的参数。在第二组S1应力下发生6件失效，用来拟合加速系数。试验结束时18件样本发生失效，剩余6个样本。

试验方案见表3。

表3 威布尔分布加速可靠性试验方案

对S2应力下的失效数据进行分布检验，假设检验结果服从威布尔分布。

利用S2应力下的失效数据，进行威布尔分布参数拟合，得到S2应力下的η2和m2。

在S1应力下m1=m2，接着利用S1应力下试验数据拟合威布尔分布的参数η1。

根据η2和η1可以求得加速因子，

若产品施加的电应力，寿命特征与电应力的关系满足逆幂率模型。根据式（4）用加速因子α2,1和应力S2和S1可以求解逆幂率模型指数n。

根据逆幂率模型的指数n，试验应力S2和实际工作应力S0，寿命特征η2，可以求解实际工作特征寿命η0，实际工作应力下寿命分布参数m0=m2。

根据威布尔分布参数η0和m0，可以求解实际工作应力下可靠度指标R0(t)。

4 某电器加速可靠性试验案例

4.1 某电器可靠性参数

某电器寿命服从威布尔分布，正常工作电压24 V，最高工作电压36 V。在不同电压下工作寿命特征服从逆幂率模型。设计加速可靠性试验，求解正常工作电压24 V，工作500 h时，某电器工作可靠度能达到多少？

4.2 某电器加速寿命试验条件

采用步退应力加速可靠性方案，试验样本选24件。试验应力选择S2=36 V，S1=31 V，试验选择定数截尾。在S2应力下发生12件样品失效时，第一阶段试验停止，转为S1应力继续试验。S1应力下出现6件样品失效时，试验结束。

4.3 试验数据

仿真试验数据见表4。S2应力下共12件产品失效，第119.7 h第一阶段试验结束。剩余样品接着在S1应力下进行试验，共6件产品失效，第96.5 h试验结束。

表4 步退应力试验失效数据（时间h）

4.4 数据分析计算

S2应力下的失效时间进行直方图绘制，如图1所示。S2应力试验数据用Matlab函数wblplot绘制威布尔概率分布图，如图2所示，可以看出试验数据在威布尔概率图中符合对数线性关系。图1、图2说明产品失效服从威布尔分布。

图1 S2应力失效数据直方图

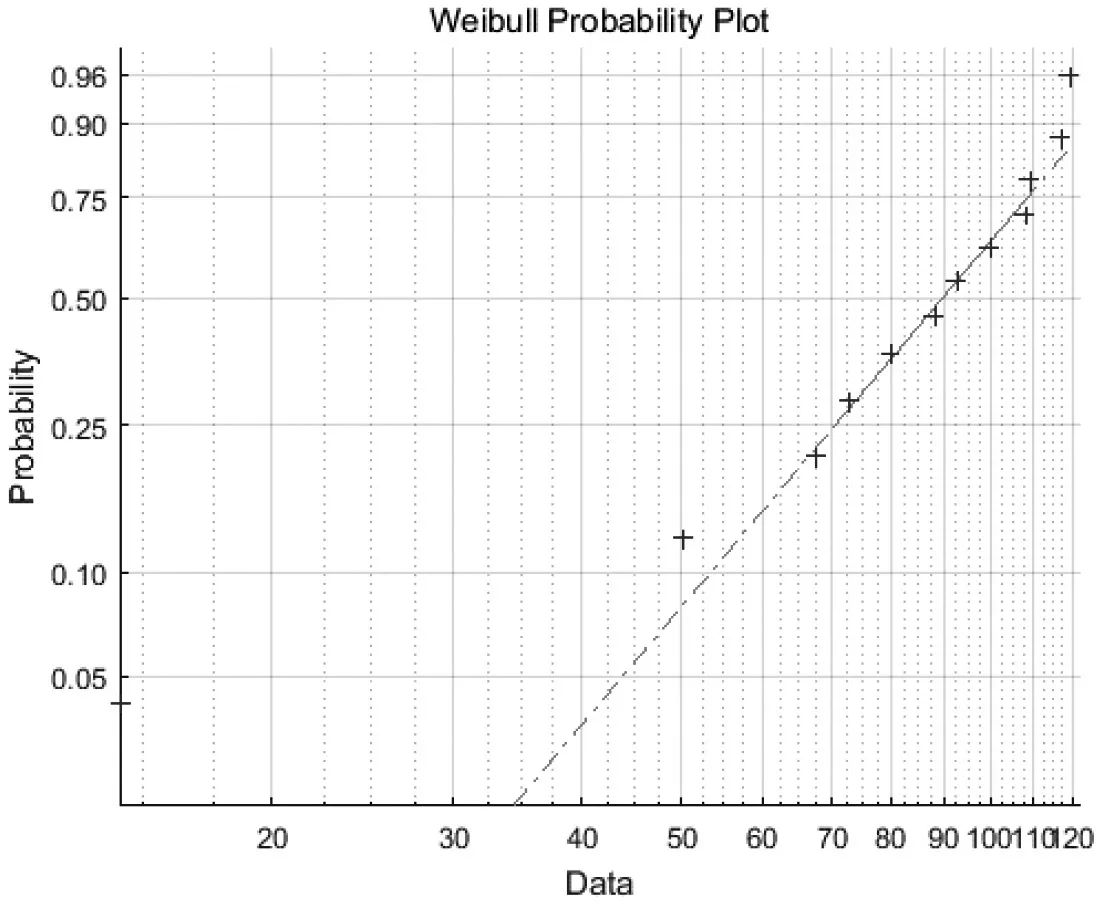
图2 S2应力失效数据威布尔概率分布图

根据威布尔分布累积概率失效公式（8），应用S2应力下失效数据，拟合得到威布尔分布特征参数值：

m2=2.62，η2=140.3 h，参数拟合曲线见图3。

图3 S2应力下失效数据威布尔分布拟合

在S1应力下失效数据威布尔概率分布图见图4，失效服从威布尔分布。

图4 S1应力失效数据威布尔概率分布图

S1应力下失效数据符合威布尔分布，形状参数与S2应力下相同，m1=m2=2.62。依据S1应力下失效数据拟合威布尔分布特征寿命η1=288.4。

根据式（9），可以计算得到S2应力与S1应力的加速因子：

根据式（4），可以计算得到逆幂率模型指数n=4.83。

根据式（4），可以计算得到S2应力与正常工作应力S0的加速系数：

可知正常工作应力下，产品失效服从威布尔分布，m0=m2=2.62，特征寿命：

根据式（8），可以计算得到某电器工作500 h时的累积失效概率：F(500)=15.2 %；可靠度R(500)=84.8 %。

5 结论

1）本文给出了服从指数分布或服从威布尔分布的产品，应用步退应力开展加速可靠性试验的具体方案。服从指数分布的产品给出指定置信水平下，评估MTBF单侧置信下限的加速可靠性试验方法。服从威布尔分布的产品给出使用最少的样本量，满足指定置信水平和特征寿命预测精度的加速可靠性试验方法。

2）通过寿命服从威布尔分布的某电器加速可靠性试验案例，介绍了步退应力加速可靠性试验方案的具体实施过程及数据处理方法。