直线伺服电机的多目标优化控制方法*
白继刚 , 张 泉
(1.包头长安永磁电机有限公司,内蒙古 包头 014030;2.内蒙古自治区先进永磁电机及其控制技术企业重点实验室,内蒙古 包头 014030)
直线电机种类繁多,控制方法各异,其中直线伺服电机作为直线电机的一种,与普通的旋转伺服电机控制方法相似,主要用于对直线运动精度与速度要求较高的场合[1]。直线伺服电机有着较为昂贵的价格,具有简洁的机械结构以及不可代替的加速度等优势,因此该电机在发达国家得到广泛的应用。从国内的应用现状分析,仅仅在个别需快速反应的高精尖产品中有所应用。从当前的情况来看,非圆截面零件数控加工得到了广泛普及和运用。结合非圆加工处理来说,中凸变椭圆活塞外圆的车削加工最为常见。通常情况下,可以将PTC活塞数控车削系统当成主要的数控机床,有助于发挥出其良好的功能和作用,还能够用作车制钢质靠模。由于直线伺服刀架属于PTC活塞数控车削系统当中不可或缺的零件之一,主要将音圈直线电机当成驱动源[2]。实际上,在音圈直线电机的管控方式方面,存在大量的研究论著与文献,然而在具体运用的过程中,依然呈现出诸多的问题与不足有待处理。一方面,因为被控对象出现了很大的非线性情况,使得设备所处的周边环境被电磁所干扰,所以设计控制器时,应该参考系统的稳定性、抗干扰性等因素。另一方面,实际运用时,既明确了在数控系统直线伺服刀架带宽方面的规定,又依靠系统的各种作用,使直线伺服刀架的动静态刚度同样需要很高的要求[3]。受到以上情况的影响,在进行操作的过程中,对于控制器参数的整定环节,一般需要进行人工试验,但是仅凭借经验加以处理会耗费大量的时间,从而影响到最终的效果。因此,合理运用直线伺服电机的多目标优化控制方法可谓十分关键。
1 直线伺服电机系统结构
直线伺服电机是可以将电能直接转换成直线运动机械能的传动装置,当前主要集中应用于电力、航天及铁道等多个领域。其中,BAYSIDE公司的IC11-030A1型直线伺服电机较为典型,其具有推力大、精度高的特点,成为了国内首选电机类型。电机侧面安装的光栅尺,能够有效地将电机位置变化量传送给驱动器和控制器,以实现直线伺服电机的闭环控制目标[4]。驱动器选用科尔摩根公司SERVOSTAR驱动器系列的CE06200,运动控制器为该电机的控制器,其主要用于闭合位置环。
2 直线伺服刀架对应的数学模型
对于直线伺服刀架而言,受控对象涵盖了直线电机驱动器、直线电机、弹簧刀架等。在这当中,无论是直线电机,还是弹簧刀架,均属于直线伺服刀架不可或缺的执行部件。
在闭合磁路当中,主要包括了直线电机的铁心1、磁铁、铁心2、磁隙等组成部分。其中,铁心1、铁心2之间存在的磁隙是非常小的,有利于在磁隙当中产生一个非常相似的匀强磁场。通常情况下,在直线电机动子的部分,则涵盖了线圈、刀杆、弹簧以及车刀等进行固连的部分。一般而言,依据相关电磁理论,从中能够看出,如果在线圈当中出现电流现象,此时线圈处于磁场当中必然受到力的作用影响,而动子受到电磁力、弹力一起的作用影响,造成刀架平移一段位移[5]。其中,电磁力和线圈当中的电流属于正比的关系,线圈当中的电流和直线电机驱动器管控电压呈现出一定的正比例关系。
因为阻尼C值较小,需要将直线电机、弹簧刀架视为一个小阻尼的二阶系统,相应的动态响应性能、抗切削力干扰能力等均不够理想,无法达到科学管控刀架的效果,缺少一定的高效性与准确性。以增强伺服系统的性能为目的,主要运用了速度、位置双闭环反馈控制的方式[6]。在这当中,内环是速度环,应用了比例管控的形式,旨在进一步增强伺服刀架迅速响应的性能,使系统的动态刚度也得以提升;而外环是位置环,旨在达到提升系统跟踪精度的目的,推导出被控对象的传递函数具体如下:
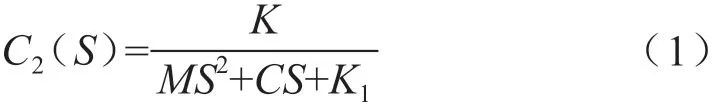
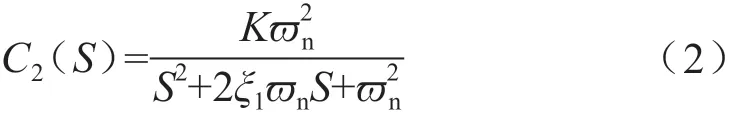
或者为:因此,在被控对象模型当中,未知参数是弹簧刚度K1,固有频率ωn,增益K,阻尼系数ξ1,主要运用系统辨识的方式进行计算。
3 基于系统稳定性的多目标优化控制分析
3.1 合理选取优化目标函数
活塞外圆加工精度的影响因素非常多,在进行工作时,直线伺服刀架的定位精度所产生的影响也十分大。能够体现直线伺服刀架定位精度的指标具体如下:其一为刀架的动态响应性能;其二为抵抗切削力干扰方面的能力。其中,直线伺服刀架的动态响应性能需要采用式(3)进行合理评估:
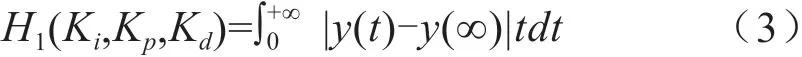
从式(3)中可以获知,y(t)代表的是系统单位阶跃响应;y(∞)代表的是系统单位阶跃信号作用下的稳态输出。
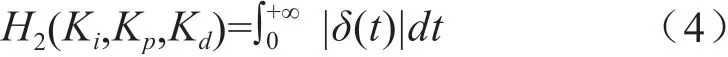
通常情况下,直线伺服刀架的抵抗切削力干扰的能力,可以采用式(4)进行准确评估:结合式(4),δ(t)代表的是刀架基于单位切削力脉冲作用下的响应。如此,能够说明直线伺服刀架综合性能的目标函数,主要通过式(5)进行表示:
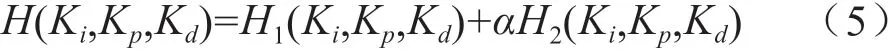
根据式(5)可以获知,α代表权重因子。实际上,式(5)还能够表示如下:
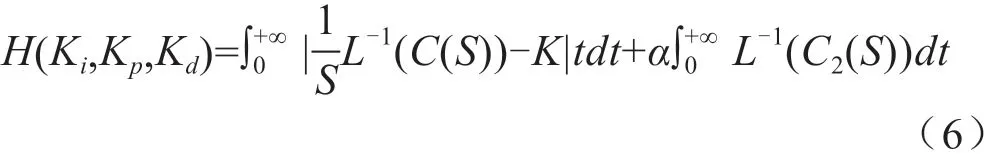
由于以直接的形式对式(6)当中显式表达式L-1(C(S))与L-1(C2(S))进行求解的难度非常大,所以通常需要运用MATLAB库中的Step(sys)函数加以准确计算。
3.2 明确相应约束条件
通常情况下,在被控对象当中涵盖了功放、电机以及弹簧刀架等,均属于高阶的非线性系统,运用公式(2),单纯以便于进行处理作为主要目的,针对被控对象运用的线性化可以忽略。受到以上原因的影响,借助相关稳定性理论,可以有效明确,在稳定约束条件下,容易发生和实际不符的结论[7]。经过反复实践可知,导致系统内环失稳的原因在于速度环的反馈增益太大,而外环失稳是数值太大所导致的。鉴于此,可以构建下述约束:

根据式(7)可以获知,Kp0、Kd0是确保系统存在稳定裕度的最大Kp、Kd数值,然后依据从前的经验进行求解。
3.3 最优化问题的科学计算
对于直线伺服刀架控制系统的相关优化问题,通常能够归纳如下:通过准确求解合适的控制参数其中代表积分项参数代表比例项参数表示速度前馈参数,在符合式(7)相关要求的基础上,可以让式(6)拥有最小值。在对该问题进行求解计算之前,首先应该引入无约束优化问题,然后求解出适合的参数,让式(8)同样存在相应的最小值。
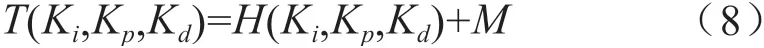
在式(8)当中,
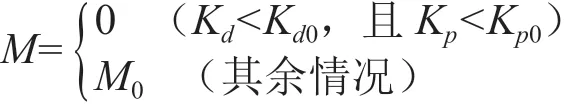
通常情况下,如果M0足够大,无约束优化问题式(8)和约束优化问题式(6)的解是相同的,如此,能够确保所获取结果的正确性。结合式(8)可以获知,通过科学运用无约束优化问题,能够借助单纯形方法进行计算[8-10],再借助相关函数库,从中能够获得单纯形方法的计算程序。
4 具体案例的仿真分析
以深入掌握经过优化之后直线伺服刀架的性能、权重因子α带给其动态响应性能、抗切削力干扰能力等方面的影响作为目的,选用实际被控对象进行仿真分析和探究。通过仔细测试,可以了解被控对象的相关物理参数,如表1所示。而表2代表的是各个权重因子α获取的优化控制参数。

表1 被控对象的相关物理参数
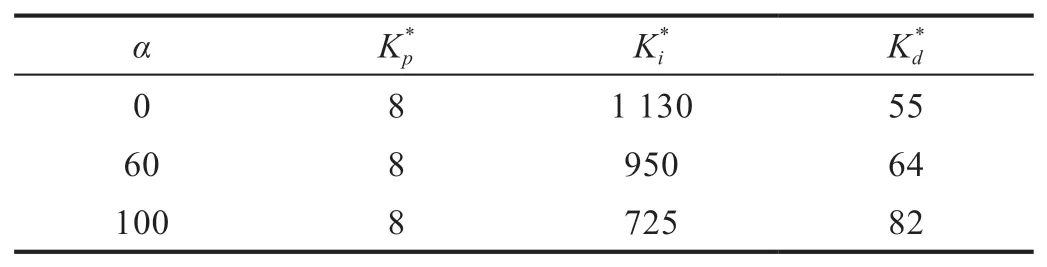
表2 各个权重因子α相应的控制器优化参数
5 结束语
综上所述,依靠计算机具有的高效计算方式,可以迅速明确控制器的相关参数,并且借助仿真分析的方式,能够从中获悉,权重因子针对直线伺服刀架的跟踪、抑制切削力等方面的能力呈现出相反的状态。鉴于此,开展系统设计的过程中,应该参考系统具体的应用规定。假如系统被用于车削铝质活塞,结合其切削力很小,但对生产效率方面的要求却很高,此时应该将比较小的权重因子作为首选,以便确保系统的带宽很大,在进行零件加工处理的过程中,可以获得更快的主轴转速。假如机床只被当作加工靠模的机床时,结合车削钢质靠模通常采用小批量生产的方式,在加工的工时方面要求较低,不过车制靠模的切削力很大,所以此时需要将比较大的权重因子作为首选,以便增强系统针对切削力干扰的抑制能力。通常情况下,借助以上优化方式,对直线伺服刀架的控制器参数加以设计,不但能够有效减少人工成本,而且能更好地发挥其性能作用。

