SFC Design and VNF Placement Based on Traffic Volume Scaling and VNF Dependency in 5G Networks

Zhihao Zeng,Zixiang Xia,Xiaoning Zhang and Yexiao He

School of Information and Communication Engineering,University of Electronic Science and Technology of China,Chengdu,611731,China

ABSTRACT The development of Fifth-Generation (5G) mobile communication technology has remarkably promoted the spread of the Internet of Things(IoT)applications.As a promising paradigm for IoT,edge computing can process the amount of data generated by mobile intelligent devices in less time response.Network Function Virtualization(NFV) that decouples network functions from dedicated hardware is an important architecture to implement edge computing,deploying heterogeneous Virtual Network Functions (VNF) (such as computer vision,natural language processing,intelligent control,etc.) on the edge service nodes.With the NFV MANO (Management and Orchestration) framework,a Service Function Chain (SFC) that contains a set of ordered VNFs can be constructed and placed in the network to offer a customized network service.However,the procedure of NFV orchestration faces a technical challenge in minimizing the network cost of VNF placement due to the complexity of the changing effect of traffic volume and the dependency on the VNF relationship.To this end,we jointly optimize SFC design and VNF placement to minimize resource cost while taking account of VNF dependency and traffic volume scaling.First,the problem is formulated as an Integer Linear Programming(ILP)model and proved NPhard by reduction from Hamiltonian Cycle problem.Then we proposed an efficient heuristic algorithm called Traffic Aware and Interdependent VNF Placement(TAIVP)to solve the problem.Compared with the benchmark algorithms,emulation results show that our algorithm can reduce network cost by 10.2% and increase service request acceptance rate by 7.6%on average.

KEYWORDS Network function virtualization;virtual network function;service function chain;resource allocation;routing

1 Introduction

Fifth-Generation (5G) [1,2] mobile communication technology has significantly contributed to the expansion of Internet of Things(IoT)[3,4]due to low energy consumption,high throughput and low latency,where billions of smart devices(such as autonomous vehicles,smart sensors,virtual reality devices,etc.) can access to the Internet.Meanwhile,edge computing[5],as a distributed computing paradigm,has drawn much attention by bringing computing and storage closer to the data source.Researchers leverage edge computing into 5G[6]to deal with the amount of data generated by mobile intelligent devices,achieving less time response and saving bandwidth of remote data centers.Network Function Virtualization (NFV) [7] which decouples network functions from dedicated hardware is a critical architecture to implement edge computing,deploying heterogonous Virtual Network Functions(VNF)[8,9]on the edge service nodes.

In the NFV architecture,VNFs are implemented in software and running on NFV based equipment.When traffic arrives,it will be orderly served by VNFs,and we call these ordered VNFs as a Service Function Chain(SFC)[10,11].Each SFC is presented as VNFs connected by virtual links.We map these VNFs and virtual links to the physical network sequentially by reserving and allocating network resources to make sure that the network can provide reliable and stable services according to users’needs,which is typically known as VNF placement[12].

There has been extensive research on optimization for VNF placement assuming the SFC topology is given by users[13,14].However,in a large quantity of network systems,NFV Management and Orchestration(MANO)deploys different types of VNFs flexibly and orchestrates SFC according to different conditions of the network,which is a theoretical challenge for NFV management and network performance optimization [15,16].Improper SFC orchestration may cause resource waste and traffic jam[17].This challenge is even more complicated by the dependency relationship between VNFs and their traffic volume scaling effect.Unlike switches,routers or other network forwarding devices,some VNFs that focus on traffic detection and processing may influence the size of traffic[18].They can shrink or amplify traffic by a certain ratio,which is called traffic volume scaling factor in this paper.For example,Citrix’s Enterprise Cloud products WAN optimizer would compress the traffic before forwarding it,and the reduced traffic after processing can be as high as 80%[19].On the contrary,the satellite communication leverages BCH,a forward error correction method,to protect messages,which increases the amount of traffic by 31%because of its verification overhead[20].At the same time,the change of traffic volume will affect the computing resource cost of VNFs[21].Another important factor for SFC design is the dependency between VNFs,which means that the VNFs of a flow have constraints on the order.If VNFadepends on VNFb,the traffic flow must be processed bybbefore passing througha[22].For example,if a traffic flow needs to be securely connected to the Internet,it should traverse through an encryptor and transmit to the network before the decryption function is started[14,23].

We demonstrate our motivation in Fig.1 with an example.As is shown in Fig.1a,a traffic flowfis given with the initial volume,being 100 units.Three VNFs,FireWall (FW),Intrusion Detection System (IDS) and Wide Area Network-optimizer (WAN-opt),are set to process the traffic.Each VNF has a traffic volume scaling factor and a CPU demand correlation coefficient.FW enlarges the traffic volume to 2 times of the original one,and the computing resource cost will increase by 1 unit for every additional 100 units of traffic volume.The traffic volume after IDS processing remains unchanged,and the computing resource cost will increase by 2 units for every additional 100 units of traffic volume.WAN-opt reduces the traffic volume to 0.5 times of the original one,and the computing resource cost will increase by 4 units for every additional 100 units of traffic volume.Based on their dependency relationship,the traffic flow must be processed by IDS before traversing through WANopt.In Fig.1b,a network with 6 nodes and 7 links is presented.It is assumed that each link provides 1000 units of communication resources and each node provides 10 units of computing resources.We give a random SFC design and VNF placement as shown in Fig.1c.We can tell that the path through which the traffic flow passes contains 3 physical links(a,dandh)with their traffic volume all being 200 units,and 4 nodes (S1,S2,S4 andS6).FW is placed on nodeS1 and its computing resource demand is 1 unit based on the initial traffic volume being 100 units.It enlarges the traffic volume to 200 units on linkaandd.Similarly,IDS is placed on nodeS4 and its computing resource demand is 4 units with the traffic volume on linkhremained as 200 units.WAN-opt is placed on nodeS6 and it demands 8 units computing resource.The traffic volume out of the network is reduced to 100 units.The total communication resource cost of the network is 600 units and the total computing resource cost is 13 units.Although this placement does not violate the constraint,it wastes significant resources.Therefore,in Fig.1d,we propose an optimal SFC design and VNF placement.The path through which the traffic flow passes contains the same physical links and nodes,but the VNF placing strategy is different.Based on the placement,the traffic volume of linka,dandhis 50,50 and 50 units.The computing resource cost in nodeS1,S2 andS6 is 4,1 and 0.5 units.Compared with the VNF placement strategy in Fig.1c,we reduce the total communication resource cost from 600 to 150 units and the total computing resource cost from 13 to 5.5 units.

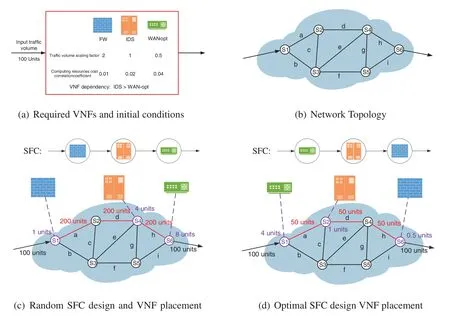
Figure 1:Examples of VNF placement

In this paper,the joint optimization of SFC design and VNF placement is studied while considering both traffic volume scaling and VNF dependency.First,the problem is formulated as an Integer Linear Programming(ILP)model and proved NP-hard by reduction from Hamiltonian Cycle problem.Next,due to its complexity,we design a heuristic algorithm called Traffic Aware and Interdependent VNF Placement(TAIVP)algorithm.In our algorithm,we first construct an optimal SFC based on traffic volume scaling factors and VNF dependency to minimize the computing resource cost.Thereafter,based on A-star algorithm,we find a feasible work path with sufficient resources and minimum hops for each SFC.Finally,to minimize the communication resource cost,we present an optimal SFC deployment strategy.Compared with the best of the benchmark algorithms,emulation results show that with the help of our algorithm,the network cost can be reduced by 10.2%on average,and the service request acceptance rate can be increased by 7.6%on average.

We summarize our main contributions as follows:

1) We study the joint optimization of SFC design and VNF placement for minimizing resource cost while taking account of VNF dependency and traffic volume change.And then the problem is formulated as an ILP model.

2) Due to the studied problem is proved NP-hard,we develop an efficient heuristic algorithm to find sub-optimal solutions.

3) Compared with three benchmark algorithms,emulation results show that with the help of our algorithm,the network cost can be reduced by 10.2%on average,and the service request acceptance rate can be increased by 7.6%on average.

We organize the rest of our paper as follows.In Section 2,the related work is briefly introduced.In Section 3,the problem is formulated as an ILP model and proved NP-hard.In Section 4,a heuristic algorithm is presented.Then,Section 5 gives the simulation results of our algorithms.Finally,in Section 6,a conclusion of our paper is given.

2 Related Work

Recently,extensive researches have emerged on SFC design and VNF placement.These works mainly focus on the following two parts.

For the first part,some of them studied the problem assuming the SFC topology is given.Ghaznavi et al.[13] presented a distributed service function chain (DSFC) to decouple a chain’s throughput from physical machines by placing VNF instances of a function in multiple machines.DSFC optimizes network utilization by coordinating the deployment operations.Ghai et al.[24]proposed an efficient algorithm to optimize the end-to-end delay of the NFV in edge networks.However the authors do not minimize the total latency simultaneously.Kuo et al.[25] studied the SFC mapping problem aiming at maximizing the total amount of requests while ensuring the capacity constraints of nodes and links.To solve the problem,they proposed an approximation algorithm.Pham et al.[26] analyzed and solved the online load balancing problem using multi-path routing in NFV to minimize the maximum link utilization of data flows in response to the dynamic changes of user demands.Li et al.[27] presented a platform named NFV-RT to provide cloud services with latency guarantees.NFV-RT optimizes the maximum of the total number of requests while ensuring the deadlines of SFC requests.They solved the problem by randomized rounding and obtained a nearoptimal solution.

For the second part,the SFC design has been taken into consideration in many previous researches.Sallam et al.[28] proposed an algorithm to optimize the application subsequence complexity and reduce the SFC maximum flow problem to the fractional multi-commodity flow problem,minimizing VNF placement cost.Fei et al.[29] suggested an approach to provision new instances for overloaded VNFs ahead of time based on the estimated flow rates.They formulated the VNF provisioning problem in order that the cost incurred by inaccurate prediction and VNF deployment is minimized.Pham et al.[30] optimized the energy and traffic-aware cost of the VNF placement for service chains,and suggested a sampling-based Markov approximation to solve it.Yu et al.[31]and Ning et al.[32]presented a mobile network architecture in software defined networking,taking account of QoS (Quality of Service) and the steadiness of different kinds of traffics.Lin et al.[33]presented a plan to orchestrate and manage VNFs by combining VNF placement and end-to-end requests which are sharing the same physical substrate network.Huang et al.[34]optimized maximum of the throughput in software defined networking by considering both MiddleBox Selection and Routing problem.Although these works above are closer to practical application,none of them considered about the dependency of VNFs,which is very common in NFV.The placement of VNFs with dependency and traffic volume scaling has been studied in several articles.Jalalitabar et al.[22,35]proposed an efficient way to design users service requests while considering the computing resource,VNF dependency and service request.Ye et al.[15]proposed a heuristic algorithm to solve the multiple SFCs design,optimize the network reconfigurations and protect the service steadiness.Ma et al.[36]addressed the NFV middleboxes placement challenge and optimized the latency and packet loss of the middleboxes in multiple traffics.Siasi et al.[37]investigated container-based mapping problem.They showed the defects of VM-based mapping and investigated mapping approach based on the containers,which took account of SFC design and VNF placement.

Compared with the previous works,the optimization of SFC design and VNF placement is focused,which is based on traffic volume scaling and VNF dependency.In this paper,an efficient heuristic algorithm is proposed which takes both communication and computing resources into consideration to minimize total network cost.The proposed algorithm divides the original optimization problem into three sub-problems,then solves each sub-problem with the optimal method.

3 Problem Formulation

In this section,the studied problem is developed as an ILP model.We provide all the definitions in Table 1.

Table 1:Definitions

Table 1 (continued)Notation Description c(m) The computing resource cost of VNF m Vi(v) A binary variable.If vertex v is visited once,it is 1;otherwise,0 Bi(e) A binary variable.If edge e is used no more than once,it is 1;otherwise,0 l The load of the link w(u,v) The weight of the link(u,v)λ The processing VNF cost f(x,t) The total cost of traffic from the current node x to the target node t g(s,x) The actual cost of going from the starting point s to the current node x h(x,t) The estimated cost of going from the current node x to the target node t Wi The weight of the link between two adjacent nodes

3.1 Network Model

The input are specifications of the policy and information of the network in our problem.The network is denoted byG=(V,E).The set of links is denoted byE.The set of nodes is denoted byV.Multiple VNFs can be placed on one node,andr(v)represents the node capacity.We useb(u,v)denoting link(u,v)∈Ebandwidth capacity.For all arrived service requests,we useFdenoting the set of all flows.Considering the characteristics of VNF,(srcf,dstf,tf,Mf)denotes the flowf∈F.srcfdenotes the source node of flowf,dstfdenotes the destination host,Tfrepresents the initial bandwidth requirement,andMfrepresents the VNF set that flowfneeds to go through.We usewmto denote the traffic volume scaling factor of VNFm,and use symbol＞to define the dependency relationship between VNFs.For example,m＞ndenotes that VNFndepends on VNFm,which means the traffic flow of the network has to be processed by VNFmbefore traverse through VNFn.Note that the VNF dependency has transitivity.It means that ifm＞n,n＞k,thenm＞k.

3.2 Mathematical Formulation

The model objective is to minimize the total network resource cost.The problem is formulated as an ILP model.

A binary variabled(m,n)is first defined to indicate the dependency between two VNFmandn:

Next,a path for the traffic flowfis selected by the controller.A binary variableis defined to represent the path passing by:

Then,for any traffic flow in the network,the controller deploy its VNFs to the appropriate physical nodes.We use a binary variableyumto present:

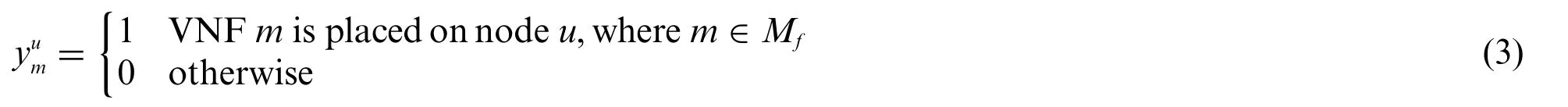
We assume flowfpasses through a multi-hop path in the network.Different VNFs being placed on the same node are also counted as one hop.If there areNhops in total,we usef(u,i)to indicate the position of theithhop,where 1 ≤i≤N:

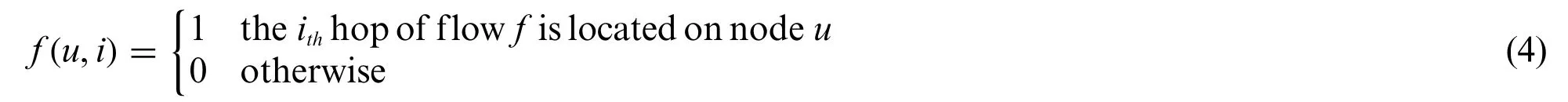
In addition,the same node is allowed to deploy multiple VNFs of the same flow to get the optimal solution when the computing resources are sufficient.Therefore,for flowf,there are the following situations:

Next,we build a mathematical model according to the constraints in the underlying network.In this section,tin(f,u)andtin(f,u)are defined to indicate the traffic volume of flowfflows into and out of nodeu.For traffic flowf,if the VNF at nodeuprocesses it,then the relationship satisfied bytin(f,u)andtout(f,u)is shown as follows:

Under circumstances that the computing resource cost of VNFs are positively related to the traffic volume,so we give the correlation coefficientrc(m),and usec(m)to indicate the computing resource cost of VNFm:

The sum of computing resources required must be no more than the node capacity provided by the physical nodeu.This can be described as:

In addition,we should guarantee that the coverage of the bandwidth capacity.We present it as follows:

Since the our VNFs are deployed on the edge servers to get close to the data source,meeting the low latency requirement of 5G,the model must have a latency constraint:

whereτcom(f)represents the communication latency on the link,andτcop(f)represents the computing latency on the edge server.Γ(f)represents the 5G-based SFC latency requirement.

To meet the first and last hops of the service request which is at the source node and destination node,respectively,we present following formula:

That each VNF must only be placed on a physical node once is assumed:

For the dependency relationship between VNFs,the following formula gives the constraints that should be satisfied after mapping.It means that for the two virtual network functions ofmandnin flowf,ifndepends onm,thennwill be deployed on the node afterm:

After we map the virtual link of the traffic flow to the physical link,we ensure the law of flow conservation in the network.This can be described as:

In order to quantify computing resources and communication resources in a unified way,we design coefficientsαandβto represent the contribution of both resources,whereαrepresents the contribution proportion of computing resources to the objective function,andβrepresents the contribution proportion of communication resources to the objective function.We first give the contribution formula of total computing resource cost:

Then,we give the contribution formula of total communication resource cost:

Finally,to minimize the total network resource cost,the ILP model is formulated as follows:

Subject to:(6)–(15)

3.3 Problem Analysis

By reduction from Hamiltonian Cycle problem,we can prove our problem NP-hard,where the VNFs order constraint is relaxed.Because the Hamiltonian Cycle problem is a classic NP-hard problem,the TAVIP problem is a NP-hard problem.We use the following theorems demonstrating the NP-hardness of the TAVIP problem.

Theorem 1:The TAVIP problem is a NP-hard problem.

Proof:The Hamiltonian Cycle problem is to determine whether there is a simple cycle that passes all vertexes inV,in which repeating nodes shall not exist.As is shown in Fig.2,consider a Hamiltonian Cycle instance with a directed graphG=(V,E),where the set of vertices is denoted byVand the set of edges is denoted byE.For each vertexv∈V,we have following definition:

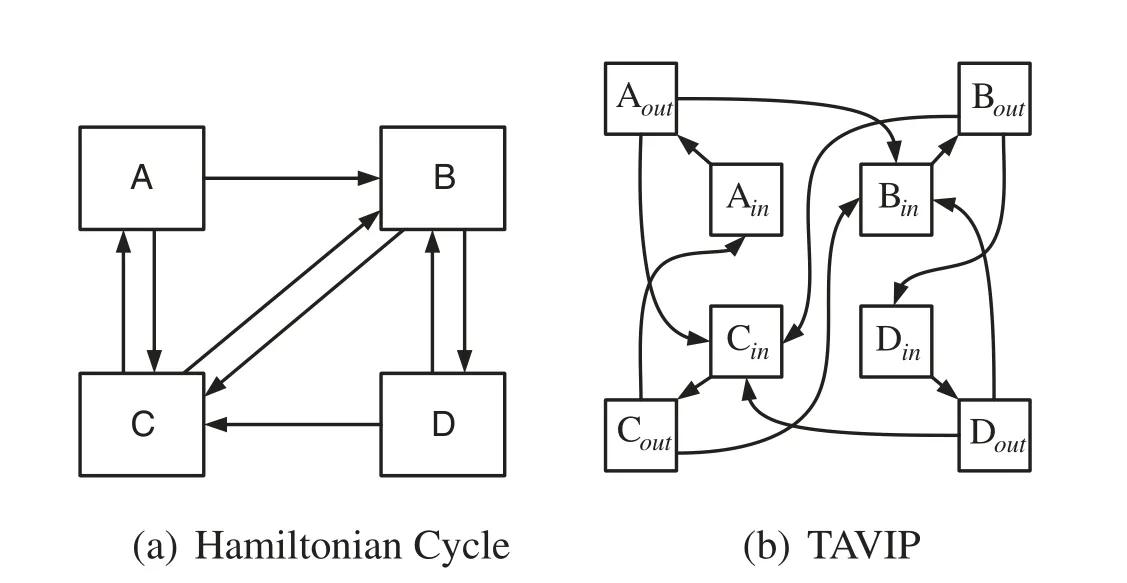
Figure 2:Reduction from hamiltonian cycle to TAPIM

For each edgee∈Ewe have following definition:

There shall exist a simple circle that contains each vertex in the graph.

We redefine our optimization problem to a route planning problem.Then we will explain that we can reduce the Hamiltonian Cycle problem to our problem.Consider a TAVIP instance with a graphG′=(V′,E′),where the set of vertices is denoted byV′and the set of edges is denoted byE′.For each vertexv∈V,two nodesvin,voutassigned with capacityC(vin)=0 andC(vout)=1 are created.The edge(vin,vout)∈E,vin,vout∈Vhas a bandwidth capacityb(vin,vout)=∞,and for its weightW(vin,vout)we have following definition:

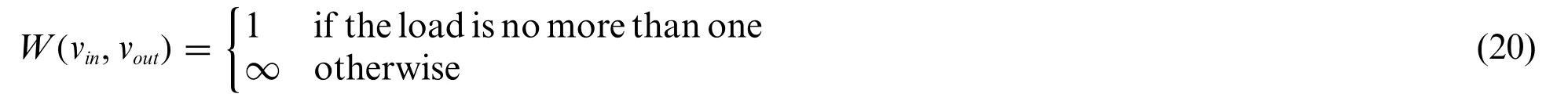
We generate a link(uout,vin)∈E′whose bandwidth capacity isb(uout,vin)=1 and weight isW(uout,vin)=0 for every edge(u,v)∈E.We give a flow f whose source and destination are both the same,Ain,i.e.,srcf=dstf=Ain.InG,nis a vertex inV.The initial traffic rate is set to one.Considering a non-ordered VNF setMwithVVNFs|M|=|V|,traffic rate changing factor of each VNFm∈Miswm=1.

Definition:We call a function f:δ1→δ2 the mapping reduction from A to B if f

a) For anyβ∈δ1,β∈A if f f(β)∈B,

b)fis a computable function.

Mapping reductions are used to reduce one decision problem to another decision problem.So if we can reduce problemAto problemBin polynomial time,we can transfer the answer ofAto the answer ofBin polynomial time.By mapping the variable of the Hamiltonian Cycle problem to the variable of our problem,we have

We can reduce the Hamiltonian Cycle problem to our optimization problem through the definition and Eq.(20).In other words,ifGhas a Hamiltonian Cycle,the TAIVP withG’andfhas a path with minimum cost of|V|.Hence,our optimization problem is NP-hard and an A*algorithm in Section 4 is designed to optimize our problem.

4 Algorithm Design

In this section,a heuristic algorithm called TAIVP is proposed.As is shown in Algorithm 1,the TAIVP algorithm has three main components.For each service request,the algorithm constructs an optimal SFC based on VNF traffic volume scaling factor and dependency by SFC Construction function(line 2).Then,in line 3,it finds a feasible work path with sufficient resources and minimum hops for each SFC by Path Planing function.In line 4,according to the influence of traffic volume scaling factors of VNFs,the SFC is deployed to the determined path by SFC Embedding function[38].Finally,in line 6,all resource cost in the network is added up by the algorithm.

Algorithm 1:TAIVP Input:G=(V;E),a set of service requests F Output:Total network resource cost Cost 1:for each service request do 2: Excute SFC Construction to construct an optimal SFC for service requests in F;3: Excute Path Planning to find the feasible mapping strategies for service requests in F;4: Excute SFC Embedding to efficiently deploy SFC to the network;5:end for 6:Cost ←add up the cost of communication and computing resources in the network;7:return Cost

4.1 SFC Construction

SFC Construction function is used to construct SFC with the lowest network resource cost while satisfying the constraint of the VNF dependency.The most original solution is to put the VNF with smaller traffic volume scaling factor in the front position.Because of the dependency between VNFs,we propose the construction strategy of combining VNFs to minimize network resource cost.We first rank all VNFs in the ascending order of their traffic volume scaling factors.When a VNF has dependency constraint,if its traffic volume scaling factor is smaller than the dependent VNFiin front of it,it must followiand we combine it withi.Otherwise the restriction has no effect in our design.As is shown in Fig.3,both sets A and B are combined VNFs.

We define two parameterswandλfor each VNF,wherewrepresents the traffic volume scaling factor andλrepresents the network resource cost of a combined VNF set (a single VNF can be regarded as a VNF set with only one VNF)with the initial bandwidth being 1.Therefore,the definition for a single VNFiis presented as follows:

For a combined VNF set with VNFiand VNFj,we have the following definitions:

To determine the order of two VNF sets without dependency,as shown in Fig.3,if set A shall be placed in front of set B,then the total cost of such deployment must be less than the total cost of set B in front of set A.We have the following formula:

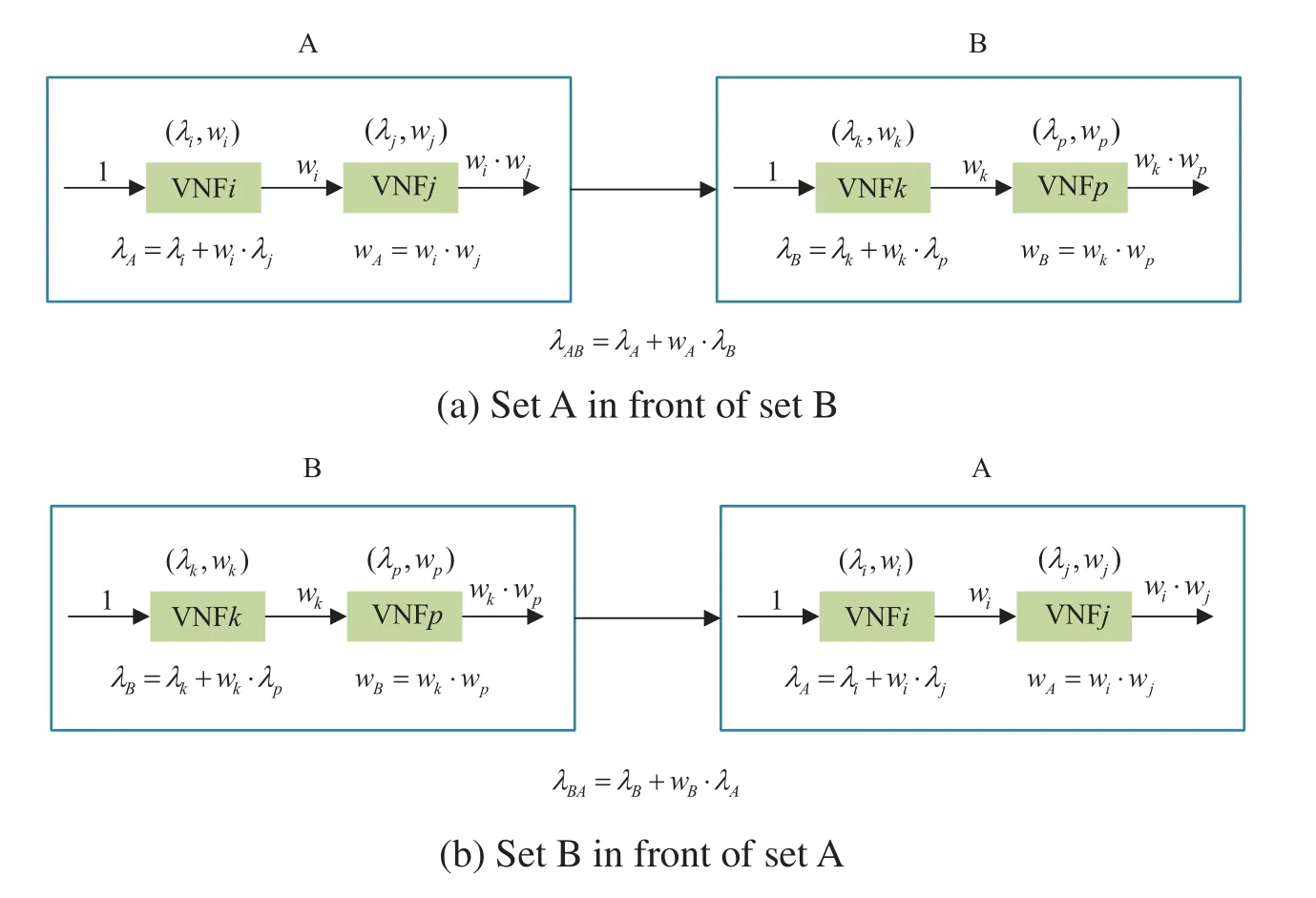
Figure 3:Placement of VNF sets

This shows that if(1-wA)/λAis regarded as an intrinsic attribute of VNF set A,and VNF with larger value should be placed at the front.

In Algorithm 2,we present the detail of SFC Construction function.The input of the Algorithm 2 is the VNF setsMf,and the output is the designed SFC.First,we calculate theλiof each VNF and sort them(lines 1–4).Then we select the VNF with highest(1-wi)/λivalue(line 6).If the selected VNF has efficient dependency restriction,we combine it with the previous VNF,update theirλandw,and then delete VNFiand VNFjfromMfand add VNFi,jto it(lines 7–12).Otherwise we add VNFito the end of SFC and delete it fromMf(lines 13–15).Finally,we will get the designed SFC with the lowest netwrok resource cost while satisfying the VNF dependency.

Algorithm 2:SFC Construction function Input:VNF sets Mf Output:SFC 1:for each VNFi ∈Mf do 2:λi ←α·rc(i)+β·wi;3:end for 4:Sort Mf by the reference of(1-wi)/λi in ascending order;5:while(Mf !=null)do 6: Select VNFi with the highest(1-wi)/λi value;7: if VNFi has an efficient dependency restriction then 8: Combine it with dependent VNFj in front of it as VNFi,j;9: λ(i,j) ←λi+wi·λj;10: w(i,j) ←wi·wj;11: Delete VNFi and VNFj from Mf;12: Add VNFi;j to Mf to remain sorted;(Continued)

Algorithm 2:(Continued)13: else 14: Add VNFi to the end of SFC and delete VNFi from Mf;15: end if 16:end while 17:return SFC

Complexity analysis:We analyze the time complexity of the SFC Construction function.Since the dependency relationship will fix the relative VNFs in order,which makes the SFC construction time shorter,we assume there is no dependency relationship in a service request.The order of any two VNFs can be determined after a round of calculation.The number of VNFs of a service request is denoted byn.The time complexity of sorting(1-wi)/λiisO(nlogn),and the time complexity of sorting VNFs isO(n).So the time complexity of the SFC Construction function isO(nlogn).

4.2 Path Planning

A-star algorithm is a commonly used heuristic search algorithm based on Dijkstra algorithm.It is popular in path planning because of its flexibility,especially in the field of artificial intelligence.It selects the expansion direction of the node reasonably through the evaluation function,and constantly searches for the best path by approaching the destination node.In this way,it can search the node with high probability first,thus improving the search efficiency of the path node.

As shown in Fig.4,we can see that it leverages an evaluation function to estimate the path cost from the current node to the destination node.The evaluation function is shown as follows:

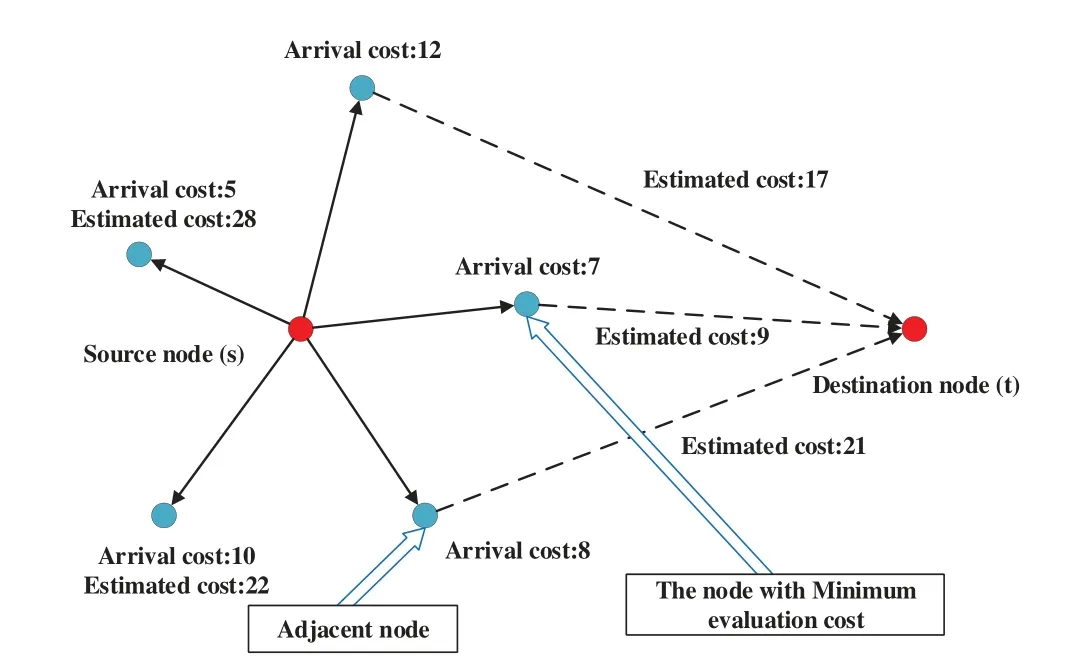
Figure 4:A-star algorithm schematic

In this formula,xdenotes the current node.tdenotes the destination node.sdenotes the source node.f(x,t)represents the total cost of the path fromxtot.g(s,x)represents the actual cost of the path fromstox,which can be obtained by Dijkstra algorithm;h(x,t)represents the estimated cost of the path fromxtot,which can be used for the algorithm to search the nodes close to the destination node first.In the process of heuristic search,it is necessary to ensure thath(x,t)is no more than the real cost required fromxtot,otherwise the result will be inaccurate,so we seth(x,t)as the shortest path fromxtot.

The purpose of path planning is to minimize the resource cost on the work path.Under the condition of SFC construction,the shorter the path,the less the link resource cost.The key point of A-star algorithm is to findg(s,x)from the source node to any accessible adjacent node,estimate theh(x,t)from a adjacent node to the destination node,and calculate the total costf(x,t).Then the algorithm selects the adjacent node with the lowest total cost and repeat the above operation until we find the shorted path.If the deployment of SFC cannot be completed by the shortest path,A-star algorithm will find a sub-shortest path for the SFC.

As is shown in Algorithm 3,we present the detail of Path Planning function.First,we arrange the service requests according to the initial bandwidth requirementtfin descending order (lines 1,2).Second,we reverse all edges of the network topology.We take the destination nodedstfas the source node,and calculate the shortest pathh(x)fromdstfto any other node(line 3).Then we create a priority queueQueueto storage nodes with the shortest distance from the node to the source nodeg(x)and the estimated costf(x).cntstores the number of times a node leaving the queue;rrecord the computing resources that nodes of path can provide(line 4).Next,we put the source nodesrcfinto the queueQueue(line 5).After that it selects the nodexwith the lowest estimated cost in the queue to determine whether the node is the destination node and the number of times it exits the queue isk.If so,the current path is thek-thshortest path from the source node to the destination node,and the algorithm ends(lines 6–14,22–24).Otherwise,the algorithm searches the adjacent nodes of nodex,and add the information of them to the priority queue(lines 15–21).

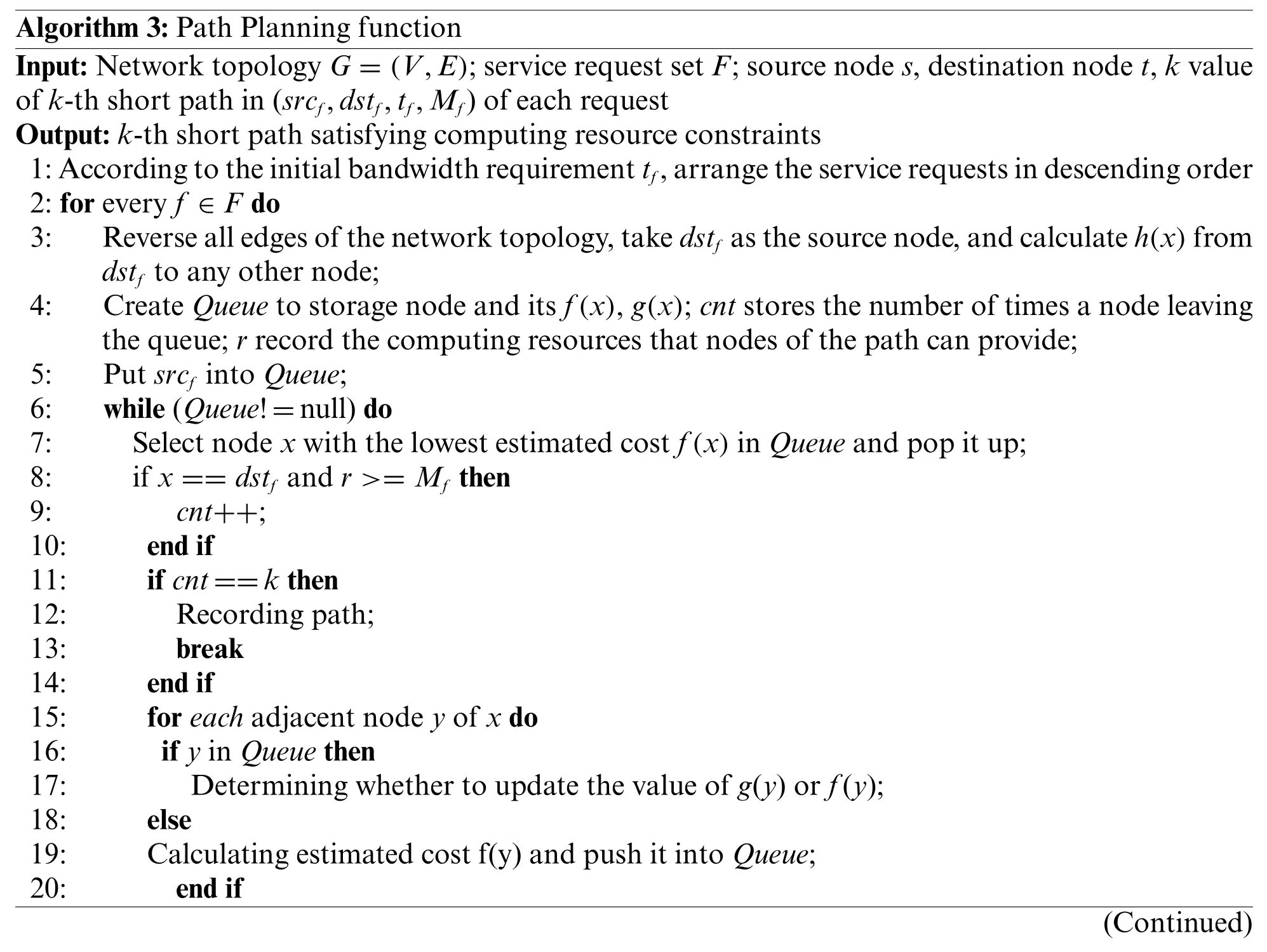
Algorithm 3:Path Planning function Input:Network topology G=(V,E);service request set F;source node s,destination node t,k value of k-th short path in(srcf,dstf,tf,Mf)of each request Output:k-th short path satisfying computing resource constraints 1:According to the initial bandwidth requirement tf,arrange the service requests in descending order 2:for every f ∈F do 3: Reverse all edges of the network topology,take dstf as the source node,and calculate h(x)from dstf to any other node;4: Create Queue to storage node and its f(x),g(x);cnt stores the number of times a node leaving the queue;r record the computing resources that nodes of the path can provide;5: Put srcf into Queue;6: while(Queue!=null)do 7: Select node x with the lowest estimated cost f(x)in Queue and pop it up;8: if x==dstf and r＞=Mf then 9: cnt++;10: end if 11: if cnt==k then 12: Recording path;13: break 14: end if 15: for each adjacent node y of x do 16: if y in Queue then 17: Determining whether to update the value of g(y)or f(y);18: else 19: Calculating estimated cost f(y)and push it into Queue;20: end if(Continued)

Algorithm 3:(Continued)21: end for 22: end while 23: Output kth short path;24: end for

4.3 SFC Embedding

Through the processing of the first two functions,we now know the SFC and work path.The problem to be solved in this stage is to ensure the total cost of the whole link is the smallest by deploying VNFs to the determined work path according to the impact of their traffic volume scaling factors on the traffic and its order.A SFC Embedding algorithm is proposed to optimize this problem.

The constructed SFC hasKVNFs in sequence with the initial bandwidth beingtf.There areNnetwork nodes on the effective work path found by Path Planning algorithm,and the node capacity provided by each node isr(v).

As is shown in Fig.5,we construct a matrix diagram ofNrows andK+1 columns.Each row represents a network node on the work path and each network node can place multiple VNFs.Each column represents a VNF of the SFC arranged in order.The first column represents empty means no VNF is placed.In the figure,the product value below each VNF indicates the total traffic volume scaling factor after the VNF is deployed.The blue dot indicates the VNFs that this node may place.There areK+1 dots in a row,indicating that each node has a opportunity to place any VNF.The line connecting the dots indicates the possible placement from the previous node to the next node.The parameters on the line indicates the weightWiof the link between two adjacent nodes in this placement case.wmultiplied by the initial bandwidthtfis the communication cost on the link.Starting from the first row,we suppose that the computing resourcer(v1)of nodev1can meet first two VNFs.Then there are only three possible placement strategies for this node:places 0,1,or 2 VNFs.The first small dot means that no VNF is placed on nodev1,the second small dot means that VNF1 is placedv1,and the third small dot means thatv1has VNF1 and VNF2 placed.Then for the second row,suppose that its computing resourcer(v1)of nodev2can meet any two VNFs of VNF1-4.Then we can also places 0,1,or 2 VNFs on this node.Fig.5 shows that there are 9 lines between first row and second row,that is,there are 9 possible placement strategies for nodesv1andv2.

It can be seen that for each row,the communication cost after thenthVNF isand so on.After the deployment of thek-thVNF,the communication cost isuntil it is connected to the last network nodevn.When the SFC deployment matrix is complete,what we need to do is to solve the shortest path from the initial dot in the first row to the last dot in the last row.The VNF withw ＜1 shall be deployed at the front of the link,and the VNF withw＞1 shall be deployed at the back of the link.For VNFiand VNFj,ifwi＞1 butwi+1＜1,we will consider them as a VNF set and calculatewi·wi+1to determine their deployment strategy.The location of the dots in this shortest path is our SFC embedding strategy.

As is shown in Algorithm 4,we present the detail of SFC Embedding function.First,we construct a matrix diagram like Fig.5(line 1).Then we design all VNF placement strategies without violating restraints (lines 2–11).Finally,we calculate the path and place VNFs to minimize the resource cost under the latency constraint in(lines 12–14).

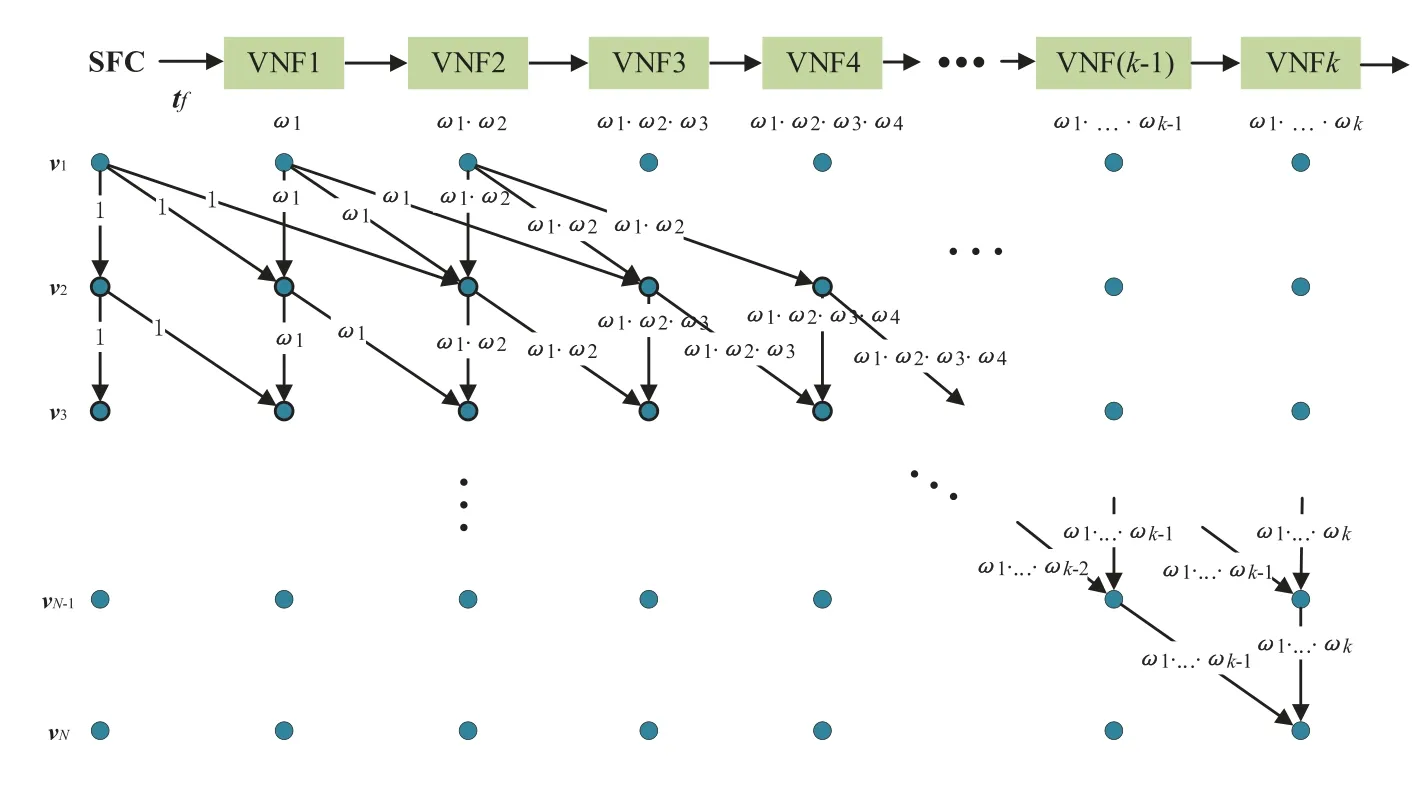
Figure 5:SFC embedding matrix

Algorithm 4:SFC Embedding function Input:SFC with K VNFs;work path with N nodes;computing resources r(v)provided by each node Output:SFC embedding strategy 1:Construct a matrix diagram of N rows and K+1 columns;2:for Each row in the matrix do 3: Designing VNF placement strategy based on the computing resource of each node;4:Calculate w of each connecting line;5:if w·tf＞b(u,v)then 6: Delete this line;7: end if 8:if c(m)＞r(u)then 9: pass this node;10: end if 11:end for 12:Determine deployment strategy of each VNF of minimal Cost under the latency constraint of Γ(f);13:Output the shortest path;14:return The dots that this path passes through

Complexity analysis:The complexity of time of the SFC Embedding function is analyzed.ndenotes the number of nodes andkdenotes the number of VNFs.The time complexity of traversing each line to decide whether to keep it or not isO((k-1)(n-1)).The time complexity of calculatingwof each VNF or VNF set isO(2k).The time complexity of SFC Embedding isO(n).So the time complexity of the SFC Embedding function isO(kn).

5 Simulation

5.1 Set Up

Our test networks,NSFNET and USNET,are shown in Fig.6 which are two typical operator networks.NSFNET topology has 14 nodes and 21 links,and USNET topology has 24 nodes and 43 links.We set the capacity of each link to 1000 units and the computing capacity of each node to 100 units.We assume that we would place totally eight types of VNFs in the network.Each traffic volume scaling factor is a random value from 0.01 to 5,and each CPU demand correlation coefficient is a random value from 0.01 to 0.1.As for service requests,we assume the nodes of network entry and export are chosen randomly.We uniformly distribute the initial bandwidth of each SFC in the span of 20 to 80 units.The number of VNFs of each SFC is assumed to be random in the range of 2 to 8.In our study,that how relatively important the computing capacity is denoted by the coefficientα,and that how relatively important the link capacity is denoted by the coefficientβ.αis set to 10,andβis set to 1.We uniformly distribute the link latency form 0.01 to 5 ms,and we set the single VNF computing latency 0.5 ms[36,39,40].

1)PerformanceMetrics:We use two metrics evaluating the performance of our algorithm:1)total network resource cost:the total cost of the network resource,which accumulates all service requests.In this paper,we refer to computing resource cost and communication resource cost;2)request acceptance rate: the percentage of requests deployed with respect to all requests;3) service response time: the interval from the service request to VNF deployment.

2) Benchmarks:We use the TOSP algorithm in[36]as our main benchmark algorithm.Besides,since there is limited existing solution,we have developed three benchmarks for reference: 1) The sorted VNFs are continuously deployed by the First-fit algorithm on the first physical node with sufficient resources in the path from the beginning;2) The sorted VNFs are continuously deployed by the Last-fit algorithm on the last physical node with sufficient resources in the path from the end;3)The sorted VNFs is randomly deployed by the Random-fit algorithm on the work path,and due to its uncertainty,the simulation results are the average values obtained after multiple experiments.These three algorithms need to determine the processing order of VNFs.Their sorting scheme is to multiply the traffic volume scaling factors of each dependency in each traffic flow in turn,and arrange the products in ascending order.In this order,all dependencies can be connected in series to form a chain.Their working paths are all searched one by one through path planning algorithm based on A-star principle.

Figure 6:Test networks

5.2 Simulation Results

5.2.1 Network Resource Cost with Different Numbers of Service Requests

The results of the network resource cost consumed by the five algorithms under different service requests in NSFNET and USNET network topologies are demonstrated Fig.7,respectively.In this scenario,the number of VNFs of each service request in NSFNET network is 3 and in USNET network is 4.The initial bandwidth is 40 units,and theKof path planning algorithm is 3.From the figure,we can see that the total network resource cost increases when the number of service requests increases,and the TAIVP algorithm costs the least network resource.On the contrary,the First-fit algorithm has the worst performance.The Last-fit algorithm can achieve a relatively better deployment for the traffic volume scaling factor of each VNF is a random value from 0.01 to 5,and the total traffic volume scaling rate of each traffic flow is the product of their multiplication.As a result,the probability of this value larger than 1 is greater so that when VNFs is deployed from the second half of the path(Last-fit algorithm),the total load is more likely to be less than that from the first half(First-fit algorithm).At the same time,it is obvious that Random-fit algorithm produces results between First-fit algorithm and Last-fit algorithm.The main reason why TOSP algorithm is not as good as TAIVP is that it only considers the minimization of communication resources,and the secondary reason is that it uses the approximate optimal method for SFC construction.Compared with the best of these four benchmark algorithm,TAIVP algorithm saves up to 9.9% and 10.5% network resource cost on average of two topologies for its smarter SFC designing.

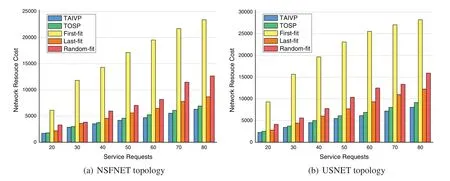
Figure 7:Network resource cost and the number of service requests

5.2.2 Network Resource Cost with Different Initial Bandwidth

Fig.8 shows the impact of the initial bandwidth change of service requests on the network resource cost.The number of VNFs of service requests is the same of the scenario of Fig.7.The number of service requests is 40,and theKof path planning algorithm is also 3.We can tell that in both NSFNET and USNET topology,the total cost of network resources consumed by the five deployment schemes will increase with the increase of the initial bandwidth,and the cost consumed by the TAIVP algorithm is the least.Compared with the best of these four benchmark algorithm,the TAIVP algorithm reduces the network resource cost by 10.1% and 9.6% on average.This is because the TAIVP algorithm is designed according to the strategy of minimizing the network resource cost in the process of building or deploying the SFC.At the same time,with the increase of the initial bandwidth,the performance advantage of the TAIVP algorithm is more and more obvious.

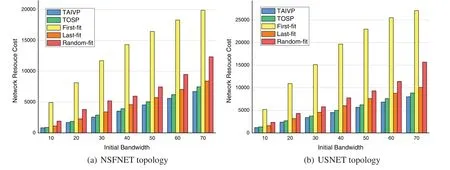
Figure 8:Network resourc e costand initial bandwidth

5.2.3 Network Resource Cost with Different α

In ourstudy,the coefficient of computing resource is denoted byα,and the coefficient of network resource isdenoted byβ.They represent two critical factors of the total resource cost in the network.Fig.9 shows Network resource costvs.αfor NSFNET and USNET.The number of VNFs of service requests isthe same of the scenario of Fig.7,and the initial bandwidth is 40 units.The number of service requests is 40,and theKof path planning algorithm is also 3.We can see that whenαis smaller (e.g.,α=0 or 5),communication resource cost is more critical than computing resource cost and has lager influence on the total network cost.While whenαis larger (e.g.,α=20 or 40),computingresource is more critical than communication resource cost and has lager influence on the total network cost.We can see that with the increase ofα,the total network resource cost also shows an increasing trend,and the TAIVP algorithm costs the least network resource.Compared with the best of these four benchmark algorithms,the network resource cost is reduced 11.3%and 10.9%on average bythe TAIVP algorithm.At the same time,with the increase ofα,the performance advantage of the TAIVP algorithm is more and more obvious.

Figure 9:Network resource cost and α

Beside the cost of network resources,we also need to consider the success rate of traffic flow deployment.Therefore,we will discuss the change of traffic flow acceptance rate of these five algorithms.The traffic flow acceptance rate is that the total number of requests divides the number of successful deployment requests,and theKvalue of path planning algorithm is set to 3.

5.2.4 Request Acceptance Rate with Different Numbers of Service Requests

The relationship between the traffic flow acceptance rate and the number of service requests is shown in Fig.10.In the figure,the number of VNF of service requests in NSFNET topology is 3 and in USNET topology is 4,and the initial bandwidth is 40 units.Obviously,when the number of service requests increases,the request acceptance rate in the network is gradually reduced.Simulation results show that the request acceptance rates of TAIVP algorithm are 6.22% and 10.27% higher than the other four algorithms on average of two network topologies.The reason is that the TAIVP algorithm generates the SFC with the lowest resource cost according to the traffic volume scaling factors of VNFs when building the SFC,while the other three algorithms only rank all the dependencies in series.Thus,when the network resources are large enough,TAIVP algorithm can accommodate more service requests.Meanwhile,compared with NSFNET network,the performance advantage of USNET network is more obvious.Especially when the number of service requests increases,the request acceptance rate of TAIVP algorithm decreases more slowly,which shows that TAIVP algorithm is more suitable for large-scale network topology than other three algorithms.

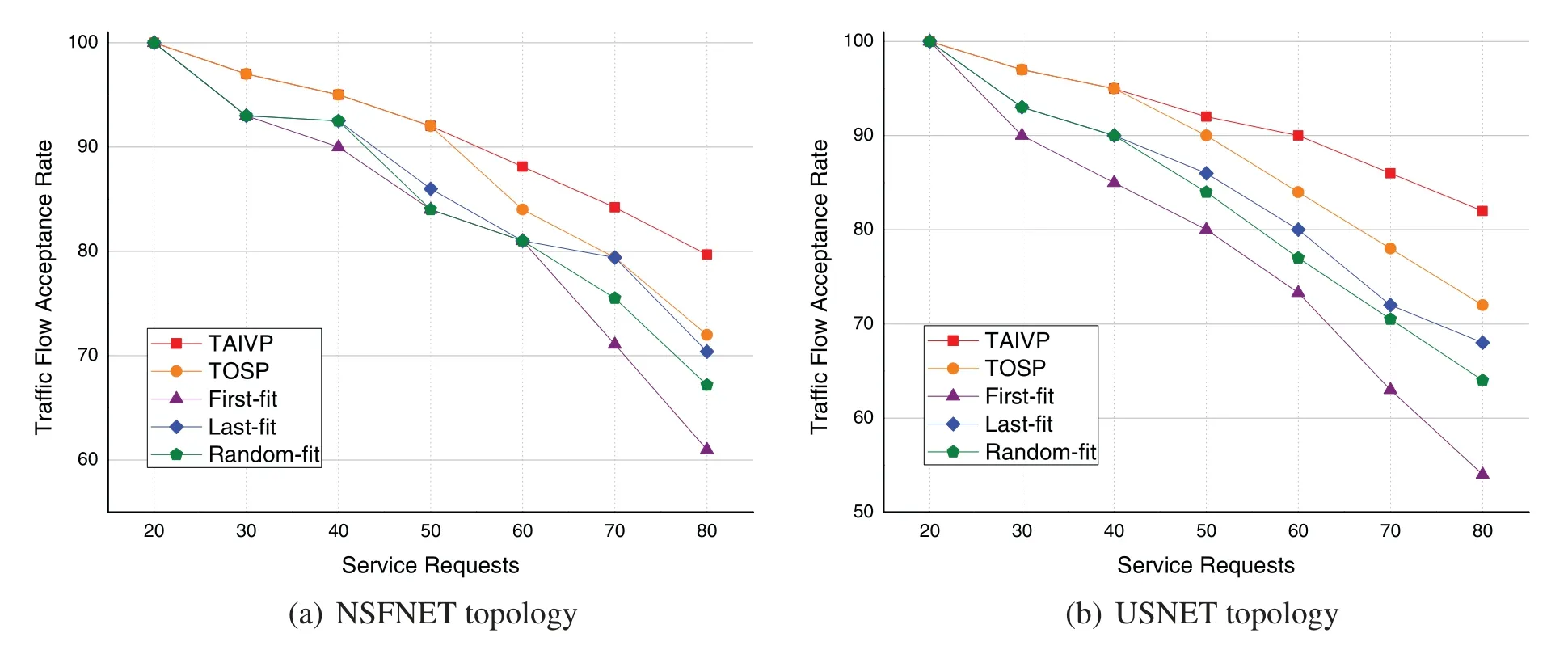
Figure 10:Request acceptance rate and the number of service requests

5.2.5 Request Acceptance Rate with Different Initial Bandwidth

As shown in Fig.11,different initial bandwidth settings also affect the reception rate of service requests in the network.In the scenario of Fig.10,the number of VNF remains,and the number of service requests is 40.We can tell that the request receiving rates of TAIVP algorithm in the two topologies are 6.21%and 6.85%higher than those of the other four algorithms on average,which shows that TAIVP algorithm is more suitable for the application scenarios of high-intensity services.So when the initial bandwidth of services is large,the network can effectively deploy more user requests.

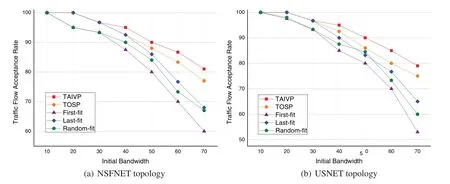
Figure 11:Request acceptance rate cost and initial bandwidth

5.2.6 Request Acceptance Rate with Different Numbers of VNFs

In addition,the number of VNFs for service requests also affects the result of the request reception rate.In Fig.12,the number of service requests in both network topologies is 20,and the initial bandwidth is 40 units.It is not hard to see that when the number of VNF increases,the acceptance rates of TAIVP algorithm are still 8.81% and 7.24% higher on average of two topologies.This is because for First-fit and Last-fit algorithm,their VNF deployment location is relatively centralized,and they do not make good use of the traffic volume scaling factors of VNFs to reduce the network resource cost.And for TOSP algorithm,its sub-optimal SFC constructing strategy can only cover 2 VNFs with dependent relationships.When the VNF number increases,more and more VNFs can be in the same dependency relationship,causing TOSP algorithm no longer valid.Therefore,some links in the network cannot provide enough resources,leading to deployment failure.It can also be seen from the figure that as the deployment of a single traffic flow becomes more complicated,the traffic reception rate is gradually decreasing,especially when the number of VNF in NSFNET network is greater than 4 and in USNET network is greater than 6.This shows that the number of VNFs that USNET network can adapt to is larger for its greater network scale and the planned work path can provide more node resources.Therefore,we can tell that TAIVP algorithm can perform very efficient in large-scale network.

5.2.7 Service Response Time

As shown in Fig.13,the service response time is also evaluated.Because NSFNET topology and USNET topology showed similar results,we only demonstrated NSFNET topology here.We first evaluated the service response time under different initial bandwidth.In Fig.13a,we can see that with the increase of initial bandwidth,the response time of all five algorithms goes up.The First-fit,Last-fit and Random-fit algorithm increase sharply while the TAIVP and TOSP increase slowly.The reason is that when the initial bandwidth increases,the successful acceptance rate of First-fit,Last-fit and Random-fit decreases rapidly.As a result,their response time increases rapidly.The successful acceptance rate of TAIVP and TOSP does not decline so fast,so their response time does not increase so fast.Similarly,from Fig.13b,we can see that with the increase of the number of VNFs to be deployed,the response time of First-fit,Last-fit and Random-fit rises rapidly,while the response time of TAIVP and TOSP does not rise so rapidly.The reason why TAIVP works better than TOSP is that TAIVP minimizes computing resources and communication resources at the same time,and calculates the most efficient results on SFC construction,while TOSP only considers communication resources,and the construction of SFC is sub-optimal.

Figure 12:Request acceptance rate cost and the number of VNFs

Figure 13:Service response time in NSFNET topology

6 Conclusion

In this paper,we jointly optimize SFC design and VNF placement problems to minimize resource cost while taking into account VNF dependency and traffic volume scaling.We first formulated the problem as an ILP model and proved its NP-hardness.Then we proposed and evaluated a heuristic algorithm called TAIVP.Finally,emulation results showed that our algorithm could reduce network cost by 10.2%and increase service request acceptance rate by 7.6%on average.There is a wide range of scenarios where our algorithm can be applied.For example,we can use this algorithm to optimize the positions of VNFs (such as computer vision,natural language processing,intelligent control,etc.)in edge computing-enabled 5G networks.However,there are still some limitations of this paper.First,we didn’t consider the QoS of the service requests,which is an important part in NFV.Besides,the heuristic algorithm can not guarantee the distance of the returned solution to the optimal one.Therefore,in future work,we first plan to modify our ILP model to take account of the QoS of the service requests.Furthermore,we plan to analyze the problem and devise an approximate algorithm with provable approximate solutions.

Funding Statement:This work was supported in part by the Open Research Projects of Zhejiang Lab(No.2021LC0AB04)and in part by the National Natural Science Foundation of China(NSFC)(Nos.62171085,62001087,U20A20156,and 61871097).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.