随机环境下电动汽车充电实时管理与优化控制算法
刘迪迪, 杨益菲, 杨玉荟, 邹艳丽, 王小华, 黎 新
(1. 广西师范大学 电子与信息工程学院, 广西壮族自治区 桂林 541004;2. 广西电网有限责任公司电力科学研究院,南宁 530000)
近年来,在环境问题和“双碳”战略的驱动下,可再生能源和电动汽车(Electric Vehicle, EV)规模不断壮大,从而受到广泛关注[1-2].然而,可再生能源固有的间歇性使得其在并网时增加了电网运行的压力[3];同时,大规模的电动汽车无序地并入智能电网进行充电可能加大智能电网峰谷差,增加配电系统网损,进而影响智能电网的稳定性和安全性[4-5].因此,如果将电动汽车作为可控负载,对其充电行为进行有效调度和管理,不仅可以降低电动汽车并网带来的负面影响[6],而且能进一步缓解可再生能源出力的强波动性给电网造成的不稳定性[7].
目前,国内外学者就电动汽车充放电调度管理主要从电网、EV用户和充电服务商3个角度开展研究.基于电网角度的研究主要考虑电动汽车并入电网之后导致的电网不稳定问题,通过对电动汽车直接调度,以最小化电网的总负荷波动优化电网的运行[8-10],并不适用于如今大规模的电动汽车调度管理现状.基于EV用户角度的研究旨在减少车主充电成本或减缓电池的寿命衰减,但可能造成可再生能源浪费[11-13].
而电动汽车与智能电网之间的桥梁,即充电站,能够聚集大量的电动汽车,可实现统筹规划电动汽车的调度问题.文献[14]提出由聚合商管理者把电动汽车的充电调度分为日前和实时两个阶段,日前阶段对总体充电电量和备用容量进行优化,实时阶段对电动汽车充电功率进行分配调度,最后对收益进行结算,但是缺少对用户需求延迟满意度的考虑.文献[15]以通勤车的固定运行时间和路线为背景,充电站协同可再生能源和储能设备,对充电站的购电成本进行优化,但该算法仅局限于通勤电动汽车的充电调度,没有普适性.文献[16]基于智能电网-充电站的两层充电架构,提出了一种考虑用户满意度和配网安全的电动汽车多目标双层充电优化模型与方法.文献[17]考虑充电站与智能电网之间的电力交易,以达到充电站利益最大的目的,但没有考虑储能设备对抑制分布式可再生能源并网对电网造成的不稳定性.文献[18] 综合考虑用户的充电需求和电网负荷水平,提出一种基于动态分时电价的电动汽车充电站有序充电控制方法,但该算法未考虑可再生能源并网.以上研究均需要提前知晓EV用户的用车信息,且需要可再生能源的出力预测等,算法复杂度较高.
本文从充电服务商的角度出发,协同可再生能源和储能设备,并计及电网的时变电价、可再生能源出力随机性和电动汽车充电可容忍时延,提出随机环境下的电动汽车充电实时管理和优化控制算法,其中可再生能源发电出力、电网电价等均为随机过程,概率分布未知.通过实时控制电动汽车的充电速率、调节储能设备的充/放电以及与智能电网的双向电力交易,在满足电动汽车的充电需求的同时,最大化自身的利益.利用Lyapunov的优化理论,所提算法不需要可再生能源出力、电动汽车需求和智能电网实时电价的统计分布信息,复杂度较低,普遍适应性好.
1 模型构建
充电服务商对电动汽车充电调度管理的模型如图1所示.其中,g(t)为智能电网与充电服务商之间t时隙的电力交易量,H(t)为t时隙充电站配备的可再生能源收集装置的发电量,b(t)为储能设备t时隙的充/放电量,ai(t)为电动汽车i在t时隙的充电需求量,i=1, 2, …,N;d(t)为充电站在t时隙分配给所有电动汽车的总充电量
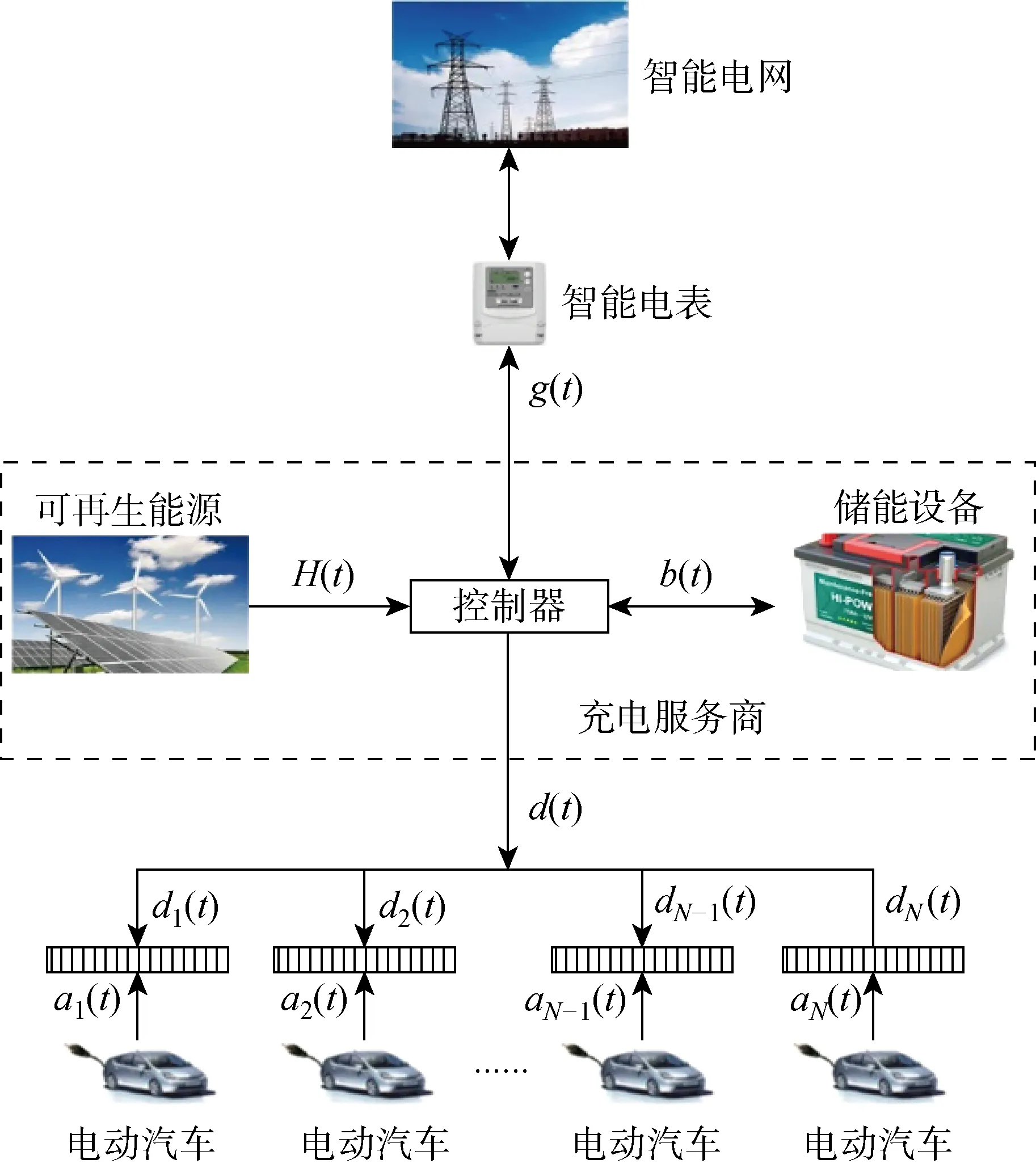
图1 电动汽车充电调度管理模型Fig.1 Management model of EV charging scheduling
该电动汽车充电站配备包括可再生能源发电设备(光伏电板或风力发电设备),并兼有储能设备,以应对可再生能源发电出力的随机性.同时充电站通过智能电表与智能电网连接,利用智能电表获取智能电网的实时电价信息.当电车与充电桩连接时,充电服务商可以获取电动汽车的充电信息,如所需充电电量、可容忍最长充电时长等.充电站的控制器根据当前可再生能源的出力情况、储能设备里的电量和智能电网的电价,实时控制电动汽车的充电速率、储能设备的充/放电以及与智能电网的双向电力交易量,以最大化充电站的利益,即最小化购电成本.
1.1 电动汽车的充电需求队列模型
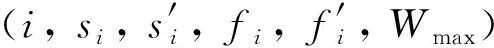
假设t时隙充电桩n的充电需求量为an(t),进入充电需求队列n(与充电桩一一对应)中,并以先进先出的方式等待被服务,用Qn(t)表示队列n中t时隙的充电需求积压,那么Qn(t)更新可表示为
Qn(t+1)=max{Qn(t)-dn(t), 0}+an(t)
(1)
1.2 电力供需模型
充电站收集的可再生能源可以由控制器直接提供给电动汽车充电,当发电量小于总充电量,即H(t)
d(t)=H(t)+g(t)+b(t)
(2)
受硬件电路最大电流量的限制,任意时隙储能设备的充/放电量b(t)以及与电网之间的交易电量g(t)均不超过最大值,即有
(3)
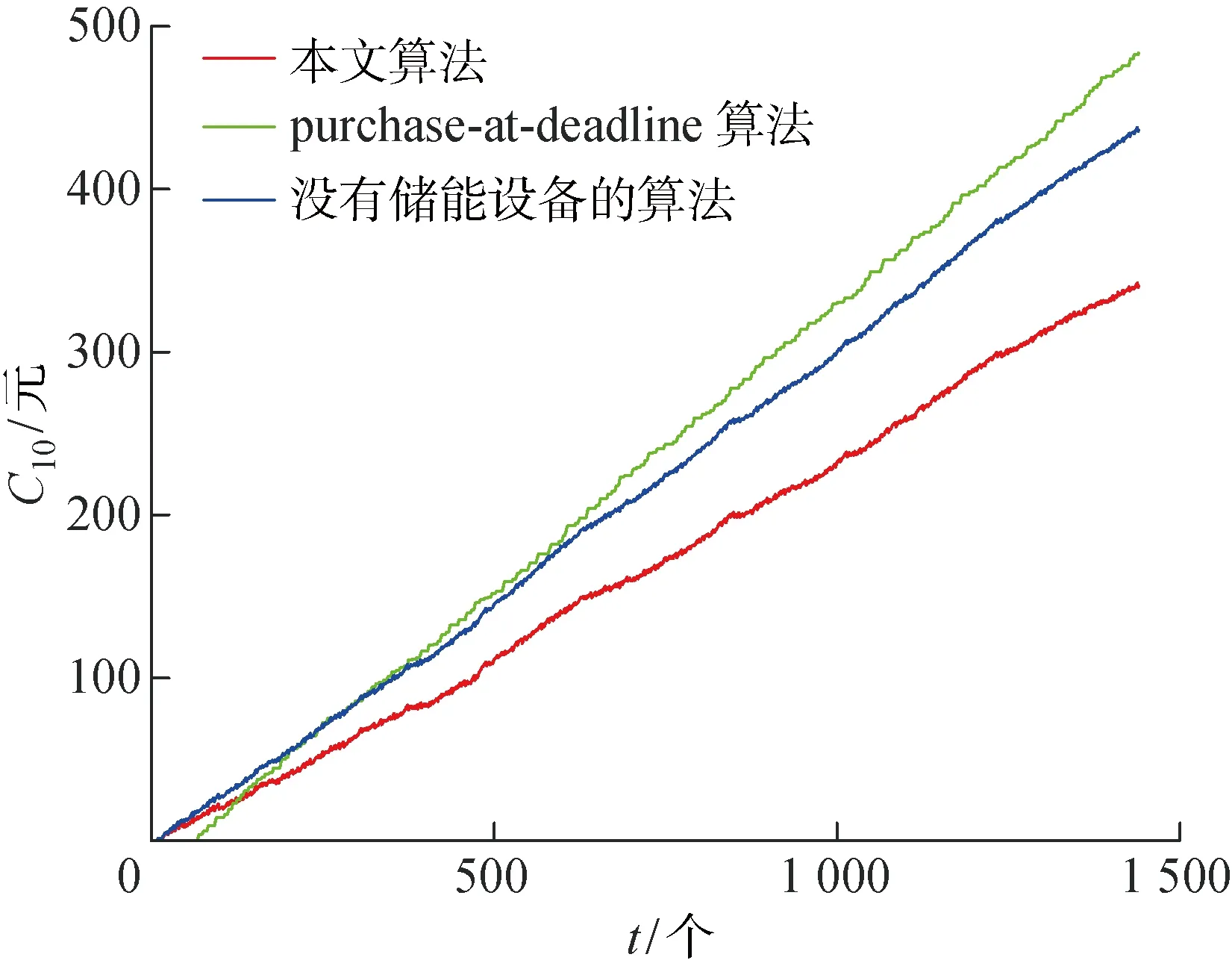
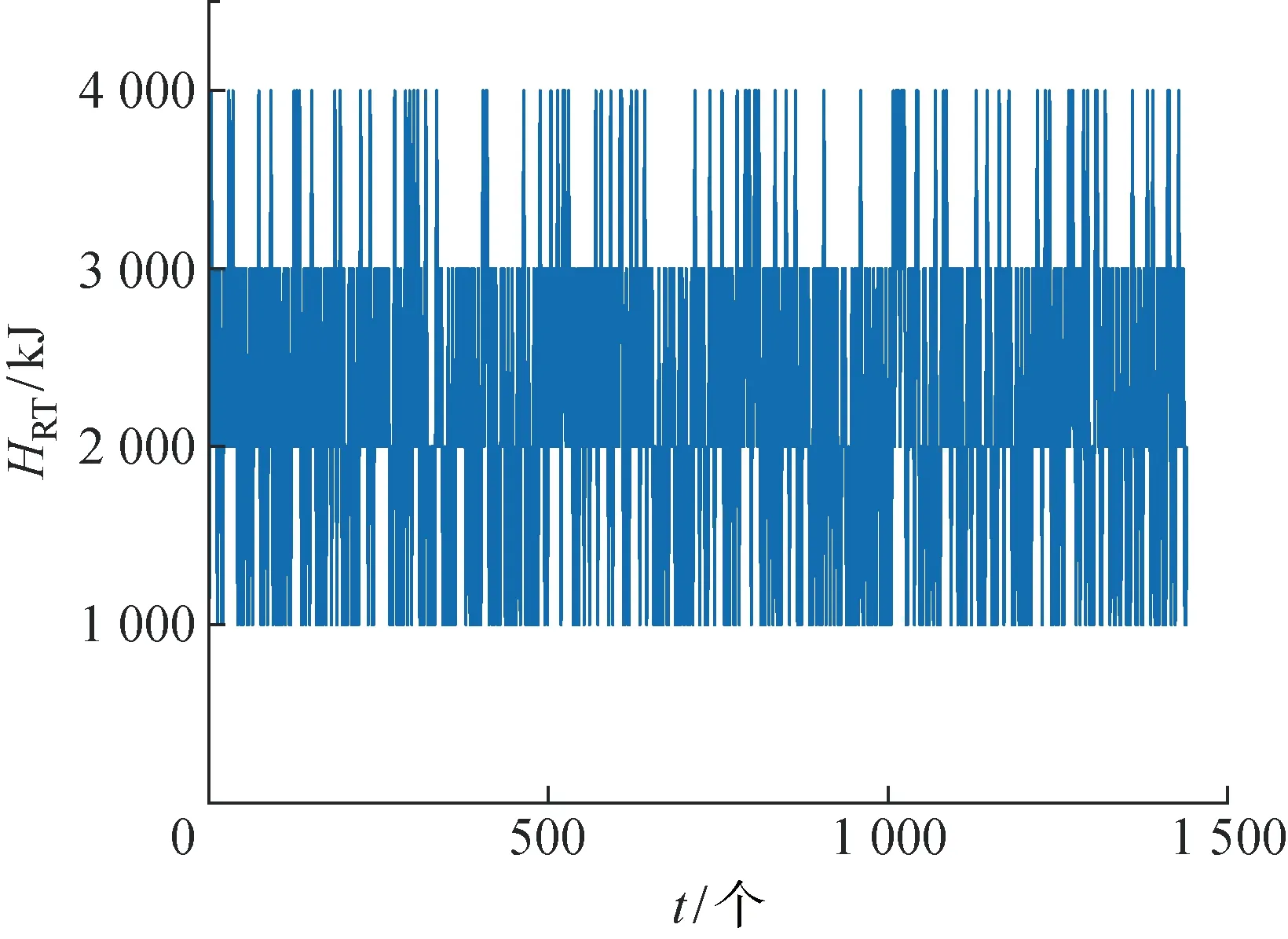
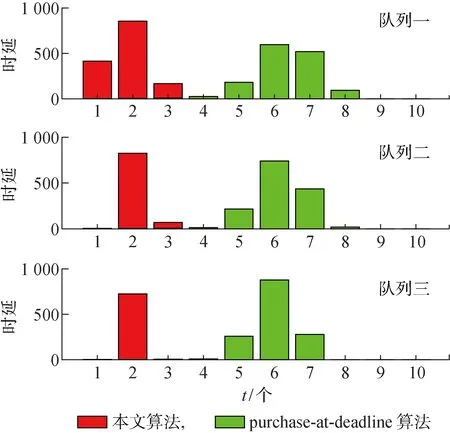
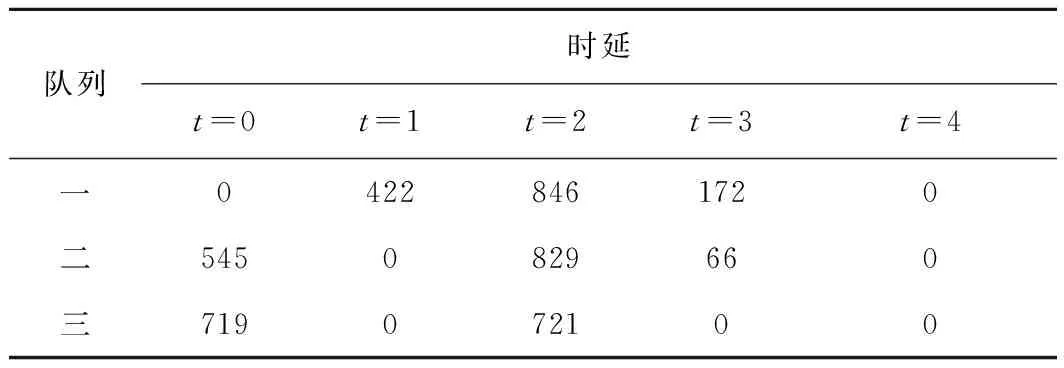
假设t时隙智能电网的电价为P(t),0 充电站的储能设备t时隙的电量记为B(t),则储能设备的电量更新为 B(t+1)=B(t)-b(t) (4) 用Bmax表示储能设备的最大容量,则充电桩控制器通过控制决策变量b(t),使得任意时隙储能设备中的电量满足: Bmin≤B(t)≤Bmax (5) 式中:Bmin为不减少储能设备使用寿命应具有的最少电量,低于该值则会因过度放电而缩短储能设备寿命,简化为Bmin=0;Bmax为储能设备存储容量最大值,高于该值则电量因无法存入而造成能量浪费. 基于以上模型,充电站根据每个充电桩当前充电需求队列的积压Qn(t)、储能设备里的当前电量B(t)、智能电网的当前电价P(t)和可再生能源装置发电量H(t),决策当前时隙储能设备充/放电量b(t)、智能电网的电力交易量g(t)和分配给每个充电桩的电量dn(t),目标是在满足电动汽车充电需求(充电时延不超过用户可容忍时限)的前提下,寻找最优决策变量(g(t),b(t),dn(t))的时间序列,最小化充电服务商的长期购电成本,该问题规划为 (6) s.t. 式(1)~(5) 0≤dn(t)≤dn,max (7) (8) (9) 定义虚拟队列Zn(t),Zn(t)的队列更新为 Zn(t+1)= max{Zn(t)-dn(t)+εn1{Qn(t)>0}, 0} (10) 式中:1{Qn(t)>0}为一个指示变量,若Qn(t)>0,其值为1,否则其值为0;常数εn表示对虚拟队列积压的惩罚,用于调节虚拟队列Zn(t)的增长速度,在实队列Qn(t)非空时,虚拟队列Zn(t)每个时隙到达εn,而虚拟队列的服务速率与实队列相同,均为dn(t). 充电桩n在t时隙的时延为δn(t),则给出以下引理. 引理1在本模型中,要保持实队列和虚拟队列稳定,则各队列积压均有上界,即Qn(t)≤Qn,max,Zn(t)≤Zn,max,那么队列n中任意时隙充电需求的服务时延最大值为 (11) 引理1表明,如果队列Qn(t)和Zn(t)具有有限的上界,那么就可以保证Qn(t)中任意时隙充电需求的服务时延都不超过δn,max.引理1的证明可参考Lyapunov优化理论[20]. 利用Lyapunov理论解决式(6)~(9)中的问题.为满足问题规划中的约束式(5),即0≤B(t)≤Bmax,将构造一个变量X(t),表示为 X(t)=B(t)-VPmax-bmax (12) 式中:V为控制参数,通过合理调节参数V来控制变量X(t),以保证储能设备中的电量保持在合理的水平,即0≤B(t)≤Bmax.由储能设备的电量更新式(4)可得出X(t)的更新方程为 X(t+1)=X(t)-b(t) (13) 定义一个矢量Θ(t)[Q(t)Z(t)X(t)],即矢量Θ(t)为实队列的矢量Q(t)=[Q1(t)Q2(t) …Qn(t)]、虚拟队列的矢量Z(t)=[Z1(t)Z2(t) …Zn(t)]和X(t)的联合矢量,则Lyapunov函数可构造为 L(Θ(t)) (14) 那么一个时隙的Lyapunov漂移函数为 ΔL(Θ(t)) E{L(Θ(t+1))-L(Θ(t))|Θ(t)} (15) Lyapunov“漂移加惩罚”表示为 {ΔL(Θ(t))+VE(P(t)g(t))|Θ(t)} (16) 式中:第一项ΔL(Θ(t))为Lyapunov漂移,表示队列积压的情况;第二项为“惩罚”,即充电服务商的购电成本.若只最小化第一项,则队列积压小即充电等待时延较小,但会导致惩罚较大即充电服务商的购电成本增加;若只最小化第二项,则可实现充电服务商购电成本最小化,但有可能无法保证电动汽车的充电需求在可容忍时限内得到满足.因此式(6)~(9)的求解则转变为最小化队列积压和惩罚的加权和,这样才能在充电等待时延不超过可容忍时延当前情况下,实现充电服务商的购电成本最小化. 引理2“漂移加惩罚”表达式满足以下不等式: {ΔL(Θ(t))+VE(P(t)g(t))|Θ(t)}≤ X(t)E{b(t)|Θ(t)}+ VE{P(t)g(t)|Θ(t)} (17) 式中: (18) 引理2的证明参考Lyapunov优化理论[20]. 利用Lyapunov理论框架,将待求解的问题转化为最小化每个时隙的“漂移加惩罚”,该表达式有界,从而等效于最小化每个时隙的不等式(17)右边的各项.除去决策变量b(t),dn(t),g(t)的无关项, 式(6)~(9)的求解可转化为 (19) s.t. 式(2),(3),(7) 式(19)是一个求解带有约束条件的线性函数最小值问题,可采用线性规划的方法求解. 由约束条件式(2)变形后带入式(19),则有 (20) (21) (22) 算法: 电动汽车充电管理和优化控制 1. 初始化:Pmax,bmax,dn,max,εn,Bmax,B(1)=0,Qn(1)=0,Zn(1)=0,V,T,N, 购电成本 SumPr=0 2.fort=1: 1:T 观测系统状态B(t),H(t),P(t),an(t) X(t)=B(t)-VPmax-bmax 线性规划求解: g*(t)=d*(t)-H(t)-b*(t) 累积购电成本SumPr=SumPr+P(t)g*(t) 储能设备电量更新B(t+1)=B(t)-b*(t) 构造的变量更新X(t+1)=X(t)-b*(t) forn=1: 1:N end end 首先从理论上对所提算法的性能进行分析和证明. 定理1在时隙t∈{0, 1, …,T-1}上,任意常数V满足0≤V≤Vmax: (23) 式中:Pmin为最小电价.则上述算法具有以下性质. 性质1队列Qn(t),Zn(t)在所有时隙都有上确界: Qn(t)≤VPmax+an,max (24) Zn(t)≤VPmax+εn (25) Qn(t)+Zn(t)≤VPmax+an,max+εn (26) 性质2充电需求队列中任何充电需求的最大时延为 (27) 性质3队列X(t)有上下界: -VPmax-bmax≤X(t)≤Bmax-VPmax-bmax (28) 由此可保证储能设备的电量约束满足 0≤B(t)≤Bmax 性质4如果H(t),d(t),P(t)在时隙上独立同分布,则在上述算法下的平均期望购电成本与最优解的差不超过C/V,即 (29) 式中:Copt为总购电成本的时间平均的最优值;C值可由式(18)给出.定理1的证明参考Lyapunov优化理论[20]. 由定理1的性质1和2可知,各队列Qn(t),Zn(t)在任意时隙都有上确界;再根据引理1得知,该算法可保证式(6)~(9)中的约束式(8)和式(9)总是成立的,即满足汽车充电需求的服务时延不超过最大时限δn,max.性质2和4表明充电需求队列中任何充电需求的最大服务时延δn,max随着控制参数V的增大而增大,而充电服务商的购电成本(目标函数)随着参数V的增大无限趋近于最优值Copt,因此充电服务商可根据用户的容忍时延折中选取参数V.由性质2可知,为了减少充电需求的最大服务时延δn,max,εn的取值应尽可能大,但一般不超过充电需求的均值E(an(t)),若给定充电需求的均值,则可取εn=E(an(t)).性质3表明了充/放电决策b(t)的合理性,使得储能设备的电量始终保持在合理水平,即Bmin≤B(t)≤Bmax,不会因过度放电造成储能设备的寿命缩短,也不会因电池容量有限造成能量浪费. 从仿真方面验证所提算法的有效性,基于MATLAB平台进行仿真验证.所提算法不依赖于可再生能源的收集和电动汽车充电需求的统计分布,为便于演示,假设可再生能源的收集服从泊松分布,对于其他统计分布,该算法也同样适用.经市场调研,发现工业电价在0.5~2.0元波动,该仿真时隙间隔Δt取10 min,时长为10 d,共 1 440 个时隙,并参考市面上的储能设备容量范围进行仿真,具体参数如表1所示. 表1 仿真参数Tab.1 Parameters of simulation 为进一步验证所提算法的有效性,将所提算法和“purchase-at-deadline”贪婪算法以及没有储能设备的算法进行比较.“purchase-at-deadline”算法是指当充电站在指定期限内只消耗可再生能源,若最后期限还未能满足电动汽车的充电需求时,则从智能电网购买电量以满足充电需求,此处设置最大期限为8个时隙.没有储能设备的场景中,当可再生能源有富余时,则将富余的可再生能源卖给智能电网,以降低充电服务商的购电成本.基于3种算法充电服务商10 d的购电累计成本(C10)对比情况如图2所示.图中,基于所提算法的充电服务商购电成本最低,“purchase-at-deadline”算法次之,没有储能设备的算法购电成本最高,分别为343元、447元和472元;相比之下,基于所提算法购电成本分别降低了23.3%和27.3%,因此所提算法的性能最好. 图2 Lyapunov优化算法与其余方法对比Fig.2 Comparison of Lyapunov optimization algorithm and other methods 可再生能源的出力具有不可控性和随机性,为了充分验证所提算法的普适性,即不受可再生能源出力影响的能力,设置可再生能源出力均值分别为 3 000,4 000,5 000 kJ共3种情况,在3种情况下进行仿真,结果如图3所示.图中,Hav为发电量H(t) 的均值.从图3可看出,可再生能源发电量越多,充电站的购电成本越低;无论可再生能源出力均值处于什么水平,基于所提算法充电站购电成本比其他两种算法均低.结果表明,本文所提算法具有较好的普适性,不依赖于可再生能源出力的概率分布,能够较好解决随机环境下电动汽车的充电调度问题. 图3 可再生能源3种情况的充电服务商购电成本比较Fig.3 Cost comparison of charging service providers in three cases of renewable energy 为验证调节参数V对所提算法性能的影响,图4给出了充电服务商10 d的购电成本随V值的变化情况.当850 图4 充电服务商的购电成本随参数V变化Fig.4 Cost of charging service provider versus parameter V 图5为储能设备的实时电量(HRT,此时V=1 400),可见基于所提算法,充/放电决策使得储能设备里的电量始终保持在合理水平,即满足约束式(5),未出现因储能设备容量有限造成电量无法存入而浪费和电量过少即过度放电缩短电池寿命的情况. 图5 储能设备中的实时电量Fig.5 Real-time amount of energy in energy storage equipment 为评估所提算法对用户等待时延的影响,将所提算法与“purchase-at-deadline”算法的时延情况进行比较.表2同时列出了本文算法和“purchase-at-deadline”算法的平均时延,可以看出本文算法的充电需求延时等待要远小于“purchase-at-deadline”算法.图6显示“purchase-at-deadline”算法的延时等待的时长集中分布在5, 6, 7个时隙,而本文算法集中分布在2个时隙,“purchase-at-deadline”算法的整体时延大于本文算法.表3和表4分别列出了依据本文算法和“purchase-at-deadline”算法的时延分布情况.从表3中可以发现本文算法中有29%的充电需求无需延时等待,而表4中另一种算法所有充电需求都需延时等待,充分体现本文算法在充电延时等待上的优越性. 表2 平均时延比较Tab.2 Comparison of average delay 图6 本文算法与“purchase-at-deadline”算法的时延比较Fig.6 Delay comparison of proposed algorithm and ‘purchase-at-deadline’ algorithm 表3 本文算法时延分布Tab.3 Delay distribution of algorithm in this paper 表4 “purchase-at-deadline”算法时延分布Tab.4 Delay distribution of ‘purchase-at-deadline’ algorithm 本文针对电动汽车充电的随机性和可再生能源出力的不确定性,研究在随机环境下的电动汽车充电调度管理问题,从充电服务商的角度出发,协同可再生能源与储能设备,提出一种基于Lyapunov理论优化的电动汽车充电管理与优化控制算法.充电服务商通过实时控制电动汽车的充电速率、储能设备的充/放电以及与智能电网的双向电力交易量,在满足电动汽车的充电和延时需求的前提下,实现长期平均购电成本最低,从而最大化收益的目标.仿真结果表明,所提算法并不依赖于可再生能源收集和充电需求的统计分布,在不同参数的设置下购电成本均小于“purchase-at-deadline”贪婪算法,并且有效降低了充电需求的等待时延.1.3 储能设备模型
2 问题规划及求解

2.1 构建虚拟队列保证延迟约束
2.2 Lyapunov优化框架
2.3 实时优化算法


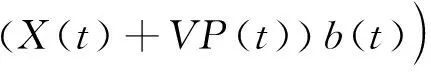
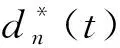


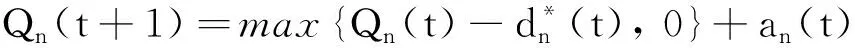

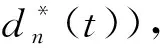
3 算法性能的理论分析
4 仿真验证





5 结语

