非接触式太阳能蒸发的模拟与分析
于 杰, 徐震原
(上海交通大学 制冷与低温工程研究所,上海 200240)
零液体排放(Zero-Liquid Discharge, ZLD)是盐水/废水处理的最终目标[1-2].近年来,反渗透、多级闪蒸和多效蒸发等水处理技术的应用在一定程度上缓解了淡水资源压力[3-5],但会产生对环境有害的高浓度盐水/废水副产品[6-8],这部分水体的处理过程面临能耗高、易缩短装置寿命以及难以彻底实现零液体排放的问题[3,9].
近年来,太阳能界面蒸发技术因其零能耗的高效产水过程得到广泛关注[10-11].该技术通过将热量集中于蒸发发生的水表面,实现了高效蒸发[11],且整体设备结构简单,在处理高浓度盐水时具有零能耗、低成本的优势[12-13].根据太阳能吸收器是否与水体接触,可将太阳能界面蒸发分为接触式蒸发和非接触式蒸发.接触式蒸发依靠吸光表面与蒸发水层直接接触来传导热量,目前已经有依靠碳基材料[14-16]和等离基元材料[17-19]强化光吸收,以及构建3D结构等方法的研究[20-23],实现了接近100%的蒸发效率.但随着蒸发的进行,盐分积累并最终在吸光表面结晶,对太阳光吸收、水分供给和蒸汽扩散产生阻碍,导致蒸发效率降低.为解决这一问题,已经有采用将吸光表面与盐结晶物理分离[24-25]、增强盐扩散回流[26-29]、构建无多孔介质的限制水层[30-31]等相关方法的尝试,但仍然依赖于直接接触的蒸发形式,能否长时间维持较高效率仍不确定.
Cooper等[32]在2018年创造性地提出一种将太阳能吸收器与待处理水体物理分离的非接触式太阳能蒸发结构,该结构通过太阳能吸收器与水体之间的非直接接触传热,完全避免了结垢问题,为高浓度盐水/废水的零液体排放处理提供了稳定方案,但其蒸发效率有待进一步提升.非接触式蒸发结构太阳能吸收器与水体之间的热交换同时涉及到辐射、对流以及传导传热过程,相较接触式蒸发更加复杂,因此非接触式蒸发结构仿真模型的建立对于指导蒸发装置的构建和优化显得尤为必要.
Cooper等[32]基于Simulink®SimscapeTM环境,采用准一维等效热阻网络法建立了瞬态传热传质模型,对于蒸发量、各部件温度的时间变化进行模拟,其结果与实验数据吻合较好,但由于该结构主要目的为产生过热蒸汽,所以假设蒸发只在水温达到沸点时进行,且水体内各处温度始终相等.而在非接触式蒸发的一般情况下,蒸发通常在水温低于沸点时进行,且水体表面至水体内部的温度分布呈现一定梯度,不可视为等温,因此该模型还存在很大局限性.Menon等[33]基于COMSOL Multiphysics有限元仿真环境建立了仿真模型,该模型适用于一般温度下的蒸发过程,且考虑了水体温度梯度的影响,但该模型为验证性模型,使用实验数据作为输入值以验证各项热损失值,无法为结构的构建优化提供相关指导.因此,目前非接触式太阳能蒸发仿真模型尚无法对一般蒸发过程的传热与传质过程进行有效模拟分析,无法对实际蒸发过程进行预测并指导实际装置优化.
本工作通过引入热阻网络模型对空气层传热、装置热损失等蒸发传热特性进行分析,引入蒸汽扩散的斐克定律对于一般温度下的蒸发传质过程加以描述,进一步基于Simulink®SimscapeTM环境和COMSOL Multiphysics有限元仿真环境构建了一种非接触式太阳能蒸发结构的稳态热阻网络模型,较好地描述了蒸发传热传质过程,可以模拟水在一般温度下的蒸发过程并对蒸发性能参数加以预测.基于该模型对于非接触式蒸发的性能进行了分析,比较了吸收-发射器与水体之间各种方式能量传递的份额关系,分析了空气层厚度和蒸汽扩散阻力对非接触式太阳能蒸发性能的影响,从而有助于为装置设计提供指导,进一步提升非接触式太阳能蒸发的性能,为其实际应用于盐水/废水的零液体排放处理打下基础.
1 非接触式太阳能蒸发稳态热阻网络模型的构建与验证
1.1 理论依据
非接触式太阳能蒸发的运行原理如图1所示.图1(a)显示了太阳能光谱能量密度和光子在水中的穿透深度.图中:λ为波长;Eλ为辐射力;Kλ为描述水对太阳辐射吸收能力的光谱吸收系数;1/Kλ为光子在水中的穿透深度,即到达该深度处太阳辐射能量被水完全吸收[34].可知,在太阳辐射能量密度最大的可见光与近红外波段,对应于太阳光谱峰值能量密度波长的光子穿透深度为40 m,即需要超过40 m的水深才能将太阳光的能量完全吸收.为克服这一问题,接触式界面蒸发所采取的策略是在水面布置一层可以高效吸收太阳辐射的中间吸收器,并依靠吸收器与水体的直接接触将热量传导至水面[14,32],如图1(b)所示.根据图1(a),在中远红外波段实现能量完全吸收所需的水深小于100 μm,而这一波长范围与50~100 ℃黑体的峰值能量密度对应波长范围相近.基于这一点,如图1(c)所示构建非接触式蒸发结构:在水面上方一定距离处放置太阳能吸收器,吸收太阳能后通过发射器将能量以集中于中远红外波段的形式辐射给水体,从而实现水体对能量的高效吸收与热量在水表面区域的集中.
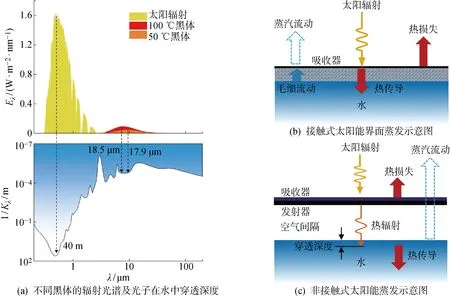
图1 非接触式太阳能蒸发运行原理[32]Fig.1 Operating principle of contactless solar evaporation[32]
已有研究提出的非接触式蒸发的结构主要有两种.Cooper等[32]提出的非接触式蒸发结构的主要目的是产生过热蒸汽,因此其吸收-发射器温度达到了超过100 ℃的高温,造成了较大的热损失,在一个太阳光照(1 000 W/m2)条件下的蒸发效率仅为24.6%.此外,过热蒸汽的产生需要构建薄蒸发水层,以保证水面温度维持在沸点,在实际运行时需要精准维持水供给[30, 35].Menon等[33]对该方案进行了改进,提出适用于零液体排放水处理的非接触式蒸发结构,其中水表面温度维持在相对较低的 42 ℃,一定程度上减小了热损失,将一个太阳光照条件下装置的蒸发效率提升至43%.由于Menon等[33]提出的非接触式蒸发结构更能代表水处理的一般情况,所以本文模型同样基于该结构建立,所涉及的非接触式蒸发模型如图2所示.图2(a)为非接触式蒸发模型的剖面结构图,模型结构的参数设置如表1所示.图2(b)为非接触式蒸发的能量平衡图,吸收器吸收入射太阳能qsolar后,通过导热将热量传递至发射器,同时在顶部产生辐射热损失qrad与对流热损失qconv;同时,发射器与水体之间的空气层、垫片也会将一部分热量qair及qs传递至水体;由于水在中远红外波段可以视为黑体,所以图中qemit为发射器与水体之间的净辐射换热量.水表面获得的净能量中,一部分能量qevap用于驱动蒸发,另一部分能量用于水表面的升温,同时在温度梯度驱动下会向下方水体传导热量qcond,并最终散失到环境中.

图2 本工作涉及的非接触式太阳能蒸发图示Fig.2 Illustration of contactless solar evaporation in this work

表1 非接触式太阳能蒸发结构参数[33]Tab.1 Parameters of contactless solar evaporation[33]
根据非接触式太阳能蒸发的技术原理,可知用于蒸发部分的能量直接决定蒸发效率,而据图2(b),在输入太阳能一定的情况下,用于蒸发部分的能量同时与装置热损失、发射器-水体间空气层传热(水体能量来源)以及蒸汽向外扩散过程有关,而对于这3个关键过程,可以使用等效热阻对其能量流动特性进行定量描述,从而可以通过构建热阻网络模型对总体能量流动进行描述,并获得相关指标参数.下面分别对于这3个核心过程进行分析.
1.2 热损失热阻等效模型
在热阻网络模型中,将水面以下大部水体、水箱、盖板等热损失途径视为热阻处理,由于部分三维组件几何结构不规则,所以按照常规计算法不易直接计算其热阻.本工作借助COMSOL Multiphysics有限元仿真软件确定上述各部件的热损失热阻数值,主要包括顶部非辐射热损失热阻以及底部水体及水箱热损失热阻.在计算顶部和底部热损失热阻时,由于所涉及的几何结构不规则,所以通过绘制三维模型,分别设置吸收-发射器温度和水面温度,根据热损失热量和温差计算热损失热阻值.图3所示为计算两部分热损失热阻的模型,图中:T为装置温度.

图3 顶部非辐射热损失热阻、水箱热损失热阻计算模型Fig.3 Calculation model of the thermal resistances of the non-radiative heat loss on the top and heat loss of the water tank
在计算顶部非辐射热损失热阻时,应用软件内置的水平板上方自然对流边界条件,通过拟合吸收器-环境温差与盖板顶部热流密度曲线斜率,由下式求得顶部有效传热系数:
Utop=qtop/ΔTtop
(1)
式中:qtop为吸收器向上方空气对流传热热流密度;ΔTtop为吸收器与外界环境温差.
在计算水体及水箱热损失热阻时,设置水箱底部边界绝热,其他边界均设置对流换热以及辐射换热边界条件,其中对流换热边界条件设为软件内置的竖壁自然对流.与计算顶部热损失热阻类似,通过拟合水表面温度-环境温差与水箱外部热损失能流密度曲线斜率,求得水及水箱热损失热阻值并由下式将该热阻归一化至水面温度和面积,求得底部热损失有效传热系数:
Ubot=qbot/ΔTbot
(2)
式中:qbot为水面向底部环境热损失热流密度;ΔTbot为水面与外界环境温差.
进一步计算顶部非辐射热损失和底部水箱热损失,并将其拟合为热阻值,所得结果如图4所示.图中:qloss为通过顶部或底部水箱热损失热流密度;ΔT为吸收器或水面温度与环境温度之间的温差.可以发现,底部水箱的热损失值近似与温差呈正比关系,根据式(2),可将底部热损失热阻近似为定值热阻;顶部盖板的热损失与温差之间并非呈正比关系,但如果不考虑图4中空心点(非拟合点)区域,当吸收-发射器温度处于60~120 ℃时,根据已有研究[32-33],一般情况下吸收-发射器的温度区间处于该范围,模拟得出结果后进一步返回验证这一点,根据图4中蓝色点(拟合点)数据,可以近似将热损失与温差拟合为线性关系,此时根据式(1)所计算的热阻值并非定值,但根据线性关系的特点,可以为热损失值增加一合适的定值,使得其与温度呈现正比关系,因此在该处定值热阻之外增加了虚拟辅助热源用以构建顶部热损失模型.

图4 顶部非辐射热损失热阻、水箱热损失热阻模拟结果及拟合模型Fig.4 Simulation results and fitting model of the thermal resistances of the non-radiative heat loss at the top and the heat loss of the tank
1.3 空气层传热模型
发射器与水体间的空气层传热是水体的能量来源,在本模型中将空气层传热处理为热阻模型.在Menon等[33]的热验证计算模型中,仅仅考虑了发射器与水体之间的辐射换热,但根据其实验所得的吸收-发射器温度与水表面温度,由Stefan-Boltzmann定律计算可得水体最大净获得热量为182 W/m2,而要达到其实验所测得的43%的蒸发效率,水体至少需要430 W/m2的净获得热量,因此水体必然还存在辐射换热以外的其他能量来源.在该非接触式蒸发结构中,由于发射器-水体间的空气层厚度非常薄(4 mm),且整个装置热输入较小,所以通过空气层传递的热量不可忽略.为考虑最大空气传热量,忽略蒸汽向上流动的对流换热效应,通过傅里叶导热定律计算在相应温差下空气层传导的热量,可得通过空气层传递的最大热量为175 W/m2,但发射器与水体间的辐射传热和空气层传热热量总和仍小于430 W/m2.非接触式蒸发结构依靠垫片保持发射器与水体之间的间距,因此必然有一部分能量通过垫片传导至下方水体,经计算,通过垫片传导的热量归一化至水面面积为139 W/m2.说明在该结构中,水体的能量来源包括发射器辐射传热、空气层传热和垫片导热共3部分.
在考虑空气层传热时,由于低温蒸汽向上扩散流动至高温吸收-发射器将产生对流传热损失,所以一定程度上减弱了空气向下的热传导过程,借助佩克莱数(Pe)进行分析,空气层的有效传热系数(Uair)计算如下:
(3)
Pe=jcp,Vb/kv
(4)
式中:kv为蒸汽导热系数;j为单位面积内蒸汽通量;cp,V为蒸汽的定容比热.在本模型中,由式(4)计算所得的佩克莱数为Pe=0.029,而当Pe趋近于0时,式(3)近似为纯导热情况,即在空气层内,由蒸汽向上扩散所引起的对流传热效应近似可以忽略.在不同工况下,kv与cp,V的变化幅度很小,而根据斐克定律,蒸汽通量j与空气层厚度b呈反相关关系,从而Pe的变化范围不大,仍趋近于0,在本模型中可以将空气层传热近似为导热状态.
1.4 考虑蒸汽扩散的稳态热阻网络模型
蒸汽扩散过程对用于蒸发部分的能量有直接影响,在热阻网络模型中,根据斐克定律将该过程处理为自定义的等效热阻.由于热阻本质上为集总热容组件,而水的蒸发以及对辐射能量的吸收只发生在水表面的一薄层区域,所以在处理水体过程中,将水表面的薄层与下方的大部分水体分开考虑,将水表面薄层区域视为等温,下方大部分水体处理为热阻而不考虑其热容效应.由于本模型为稳态模型,所以该假设不会影响其最终的稳态运行结果.该组件考虑了水在一般温度下的蒸发过程,其控制方程如下:
Q=Q1+Q2+Q3
(5)
Q1=hfgAwMwDv-air(cv,in-cv,∞)/dv-air
(6)
(7)
式中:Q为水表面获得的净热量;Q1为驱动水蒸发的热量;Q2为用于表层水体升温的热量;Q3为温度梯度驱动下水面向下方水体导热传递的热量;hfg为水的汽化潜热,取 2 407 kJ/kg;Aw为气液界面面积,取12.25 mm2;Mw为水的摩尔质量,取18 g/mol;Dv-air为蒸汽在空气中的扩散系数;cv,in为气液界面的蒸汽摩尔浓度;cv,∞为顶部盖板与外界空气界面处空气中蒸汽的摩尔浓度;dv-air为垂直于水面方向自水面到盖板-空气界面的距离;cw为水的比热容,取4.174 kJ/(kg·K);mw为表层水的质量,取 0.002 45 kg;Tw为表层水的温度;τ为时间.
将气液界面处蒸汽视为饱和状态,环境状态为25 ℃,相对湿度为50%.依据Antoine公式和理想气体状态方程计算浓度变量:
(8)
(9)
式中:psat为水的饱和蒸气压;A、B、C为Antoine常量;tv-air为蒸汽-空气系统的摄氏温度;c为蒸汽摩尔浓度;Hr为相对湿度;Ru为通用气体常数;Tv-air为蒸汽-空气系统的热力学温度.
根据式(6),Q1由蒸发率决定,而蒸发率与水表面和环境中蒸汽摩尔浓度差(cv,in-cv,∞)以及蒸汽扩散系数(Dv-air)等因素有关.
基于上述分析,在Simulink®SimscapeTM环境下构建一种非接触式太阳能蒸发稳态热阻网络模型.该稳态热阻网络模型如图5所示.图中:S为Simulink输入信号; PS为物理信号.各组件含义及计算方法如表2所示.表中:ke为吸收-发射器热导率,取237 W/(m·K);ks为垫片热导率,取 0.256 W/(m·K);As为垫片面积,取 5.39×10-4m2;Qrad为发射器-水体辐射传热量;σ为黑体辐射常数;c1为吸收-发射器比热容,取850 J/(kg·K);m1为吸收-发射器质量,取0.005 kg.
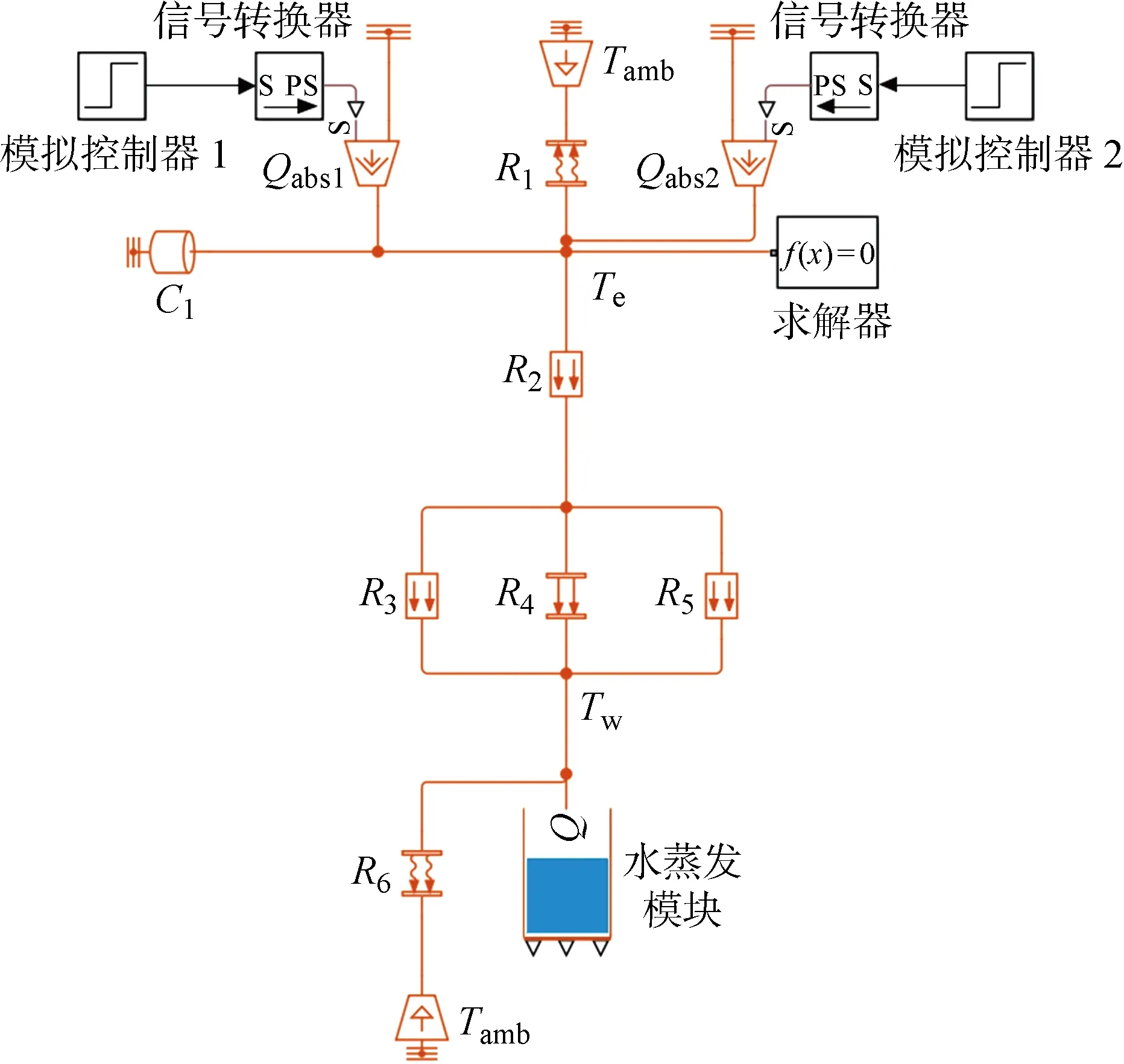
图5 非接触式蒸发结构等效热阻网络模型Fig.5 Equivalent thermal resistance network model of contactless evaporation structure

表2 等效热阻网络模型中物理量、组件含义及计算方法Tab.2 Definitions and derivations of components in equivalent thermal resistance network
1.5 模型有效性对比
根据Menon等[33]所得的水面、环境温度和相对湿度等参数,可由式(6)求出装置在稳定运行时的蒸汽-空气扩散系数为Dv-air=2.359 5×10-5m2/s,将该参数代入非接触式蒸发模型中进行求解,模型计算所得的吸收-发射器温度为70.1 ℃(实验值为70~71 ℃),水面温度为42 ℃(实验值为42 ℃),以水面面积为基准时求得蒸发效率为43.22%,考虑到垫片的存在,太阳能吸收-发射器的面积稍大于水面面积,因此使用蒸发率作为标准评价指标,模型计算所得蒸发率为 0.689 4 kg/(m2·h),与Menon等[33]实验所得的0.69 kg/(m2·h)之间的误差小于0.1%,证明本工作的模型能够较准确地预测非接触式蒸发的相关参数.
2 基于稳态等效热阻网络模型的非接触式太阳能蒸发性能分析
2.1 吸收-发射器与水体间各种方式能量传递的比较
不同于接触式太阳能蒸发依靠吸收器与水体直接接触传导热量的方式,非接触式蒸发中发射器与水体之间存在一定厚度的空气层,而水体的能量来源包括吸收器辐射传热、空气层传热和垫片导热共3种热量传递模式,要提升非接触式蒸发的效率,对于热量来源的分析尤为重要,需要对水体各项能量来源的份额大小进行分析.
在1 000 W/m2太阳光照输入和4 mm厚度垫片导热时对蒸发过程进行模拟,3种能量份额如图6(a)所示.图中:qe-w为发射器-水面间传热热流密度.将垫片导热归一化至水表面面积,可以发现,3种能量中份额最大的为垫片导热,其数值几乎为辐射传热和空气层传热的3倍,而辐射传热和空气层传热份额相当.
在规模化应用场景中,垫片导热在整体传热中的作用可以忽略,因此进一步考虑在 1 000 W/m2太阳光照输入和4 mm厚度垫片绝热时对蒸发过程进行模拟,各能量份额如图6(b)所示.可以发现,当垫片设置为绝热后,辐射传热和空气层传热的传热量均增大为考虑垫片导热情况下的2倍左右,且两者大小仍然较为接近,分别占比54.2%和45.8%,但此时整个非接触式蒸发装置的蒸发率却降低至0.545 kg/(m2·h),较考虑垫片导热情况下的蒸发率下降了约21%,这是由于吸收器与水体间传热热阻增大所导致的.
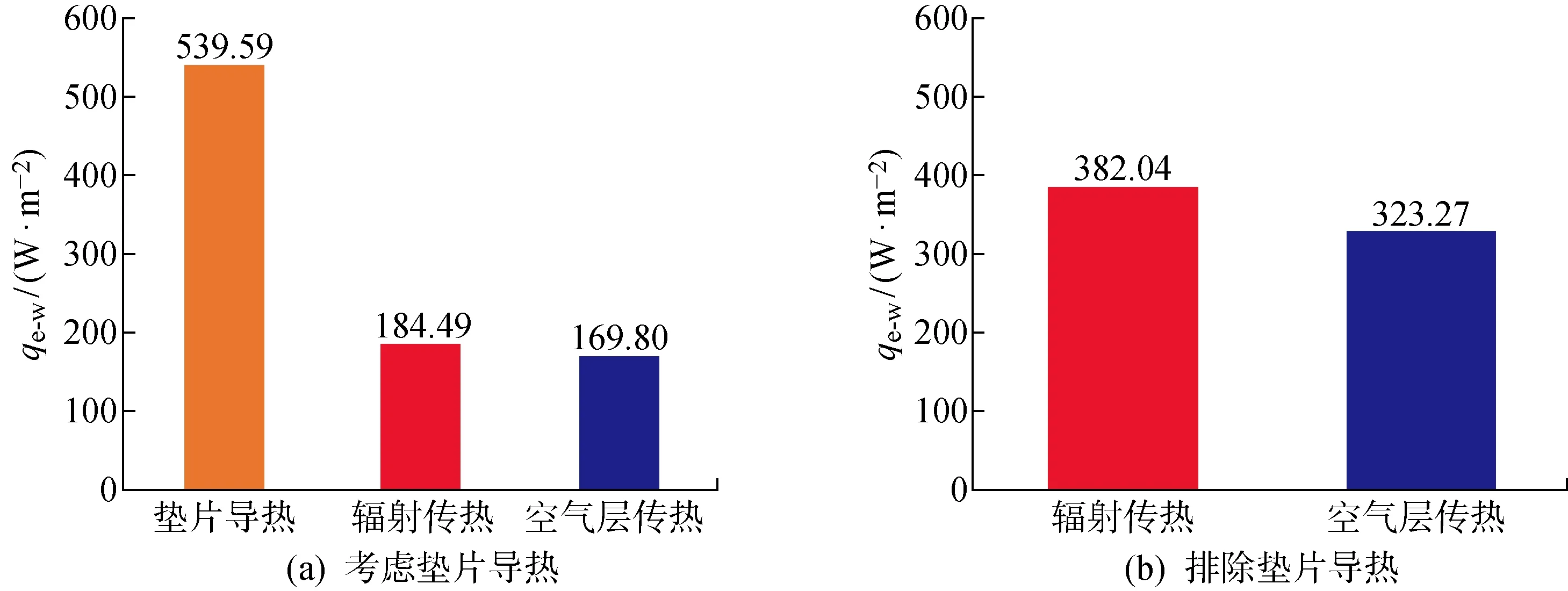
图6 非接触式蒸发水体不同形式能量来源份额比较Fig.6 Comparison of energy source amounts for water in contactless solar evaporation
2.2 发射器-水体间空气层厚度大小对非接触式蒸发的影响
非接触式蒸发结构中水面的能量来源包括垫片导热、辐射传热和空气层传热共3部分,其中垫片导热所占份额最大,如果考虑垫片为绝热,则辐射传热和空气层传热两部分热量相差不大.由此可见,在一般化的非接触蒸发过程中(不考虑垫片的导热),辐射传热和空气层传热都起到了比较重要的作用,而影响辐射传热和空气层传热的一个共同因素为发射器-水体间空气层厚度b,在连续运行过程中,由于水的不断蒸发,水位下降,空气层的厚度也相应不断增大.
在1 000 W/m2能量输入、垫片视为绝热和空气层厚度b初始大小为4 mm的基础上,随着蒸发的进行,分别对b=6,8,10 mm的情况进行模拟分析,过程中对于底部水体及水箱热阻、发射器与水体间辐射换热角系数F进行重新计算.不同空气层厚度下非接触式蒸发的相关参数变化结果如图7所示.图中:mrate为蒸发率.

图7 空气层厚度对非接触式太阳能蒸发性能的影响Fig.7 Effect of air gap thickness on contactless solar evaporation performance
图7(a)反映了空气层厚度b对吸收-发射器温度、水表面温度以及非接触式蒸发蒸发率的影响.可以发现,随着空气层厚度的增加,蒸发率呈逐渐变缓的下降趋势,10 mm空气层厚度下的蒸发率约为 4 mm 空气层厚度下蒸发率的70%.进一步观察非接触式蒸发结构中各部件温度的变化,可以发现,随着空气层厚度的增加,吸收-发射器温度呈现上升趋势,10 mm空气层厚度下的温度接近于110 ℃,较 4 mm 空气层厚度下的温度上升了近20 ℃;但水表面温度随空气层厚度的变化幅度非常微小.总体而言,吸收-发射器与水表面的温差是不断增大的,这是由于随着空气层厚度的增加,辐射传热和空气传热的热阻均增大,在环境温度一定的情况下,需要更大的温差驱动热量传递至水体内,但相对于下方水箱的热阻而言,空气层厚度增大所带来的热阻变化仍然相对较小,所以水体温度变化较小,吸收-发射器温度随之升高.
进一步考察水面两部分能量来源的份额随空气层厚度的变化情况,如图7(b)所示.可以发现,随着空气层厚度的增大,通过空气的传热量呈现明显的下降趋势,这说明尽管图7(a)表明空气层两侧的温差是增大的,但空气层厚度增加所导致的热阻增大对于整体传热的影响更为显著;另一方面,随着空气层厚度的增加,辐射传热量呈现出先略微增大后稍有减小的趋势,这表明在一定范围内空气层两侧温差增大对于辐射传热所造成的影响要大于空气层厚度增加所造成的角系数减小的影响.但总体而言,传递至水体的总热量是减小的,说明空气传热量对于空气层厚度的变化更敏感,对传输至水体的总热量影响也更大,这也进一步导致了蒸发率的下降.
2.3 蒸汽扩散阻力对于非接触式蒸发的影响
对于非接触式蒸发而言,热损失的减小意味着效率的提升.热损失是流入环境的热量,从热阻网络角度分析,如果可以减小结构内部与环境的温差或者降低水蒸发模块的热阻就可以减小热损失,达到提升蒸发效率的效果.由于水体以及水箱的热阻相对较大,所以在环境温度一定时依靠调节水面以上组件的能量分配较难实现降低水温的效果,需要考虑使水体本身温度或热阻降低的方法.在非接触式蒸发稳定运行状态下,水表面区域的蒸汽可以视为饱和状态,在此区域内温度和蒸汽浓度存在一一对应的关系,因此如果能够降低这一区域的蒸汽浓度则可以实现水温的降低,此时为获得尽可能大的蒸汽通量,根据斐克定律:
(10)
式中:J为在水面至外界的蒸汽扩散路径已经尽可能短的情况下,只有通过增大蒸汽-空气扩散系数Dv-air才有可能实现上述目标,这也意味着水蒸发模块等效热阻的减小.因此进一步分析蒸汽扩散阻力对于非接触式太阳能蒸发效率的影响.
根据模型构建部分的叙述,在考虑垫片导热的情况下,装置稳定运行时的蒸汽-空气扩散系数为Dv-air=2.359 5×10-5m2/s,而在自由扩散情况下,蒸汽-空气的二元扩散系数可以根据经验公式[36]求得:
(11)
式中:pv-air为蒸汽-空气系统压力.
水温为42 ℃时,Dv-air=2.807 6×10-5m2/s,这与实际实验中有遮挡的蒸汽-空气扩散系数相差并不大,因此在Menon等[33]的模型中,蒸汽扩散受阻的程度相对较小.在 1 000 W/m2太阳光照输入和 4 mm 厚度垫片视为绝热的条件下,对于不同蒸汽扩散阻力下的蒸发过程进行模拟,所得结果如图8所示,随着蒸汽扩散阻力的减小,即扩散系数增大,吸收-发射器温度和水表面温度都呈现出一定的下降趋势,尽管两者的温度下降幅度都较小,但非接触式蒸发结构的蒸发率呈现明显增长趋势,当蒸汽扩散系数从5×10-6m2/s增大至2.5×10-5m2/s时,蒸发率提升了2倍,这说明水蒸发模块的等效热阻显著减小.而相比于Menon等[33]模型中的蒸汽扩散系数,图8中蒸发率曲线与无遮挡工况虚线交点处的完全无蒸汽扩散受阻的蒸发率高出了约0.05 kg/(m2·h),这也表明非接触式蒸发结构的蒸发率还有一定的上升空间.从而可以得出,降低蒸汽扩散阻力是提升非接触式蒸发蒸发率的有效途径.
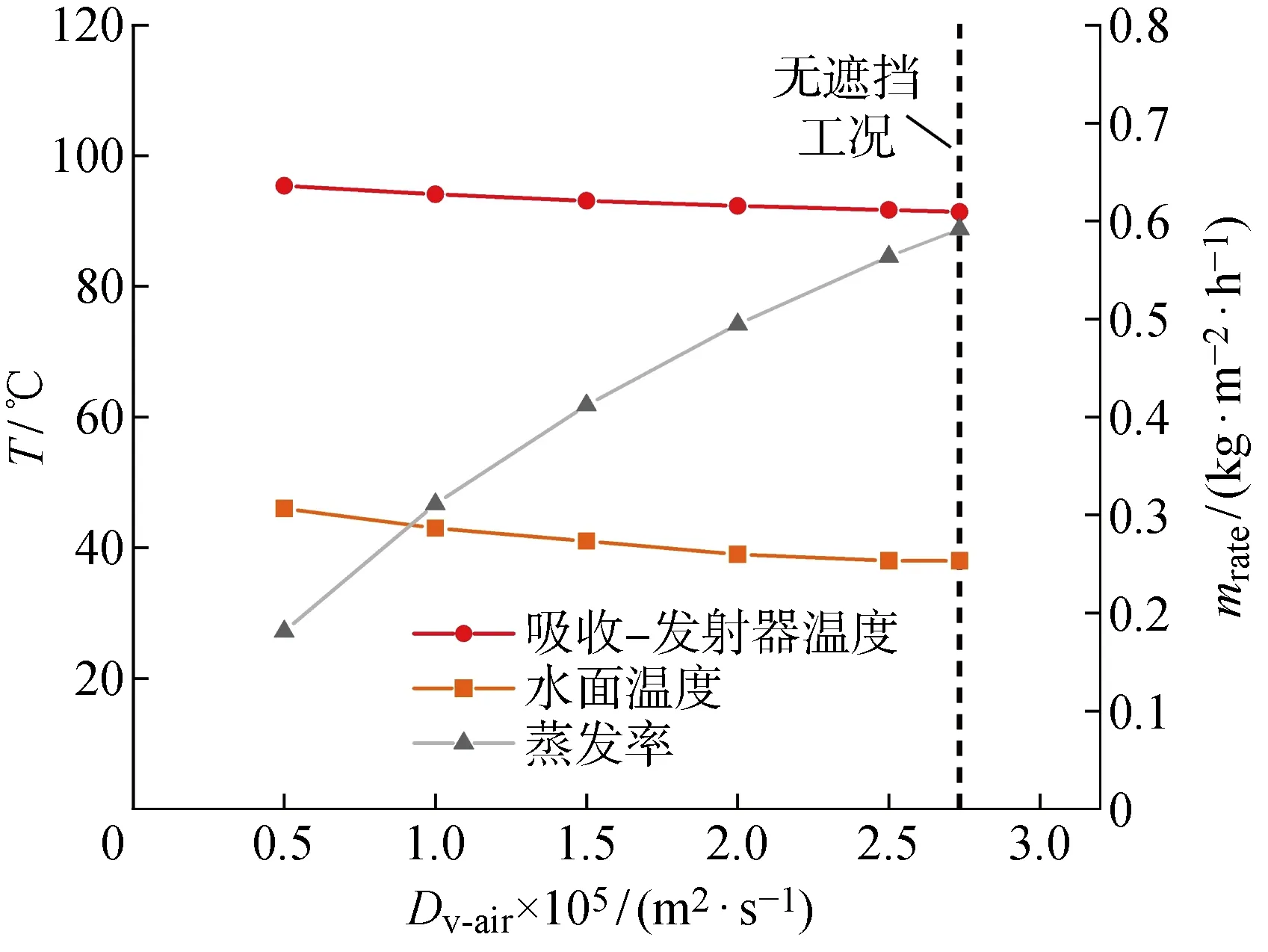
图8 蒸汽扩散阻力对于非接触式太阳能蒸发性能的影响Fig.8 Effect of vapor diffusion resistance on contactless solar evaporation performance
3 结论
非接触式太阳能蒸发为低碳、稳定处理高浓度盐水/废水以达到“零液体排放”目标提供了理想的途径,可以从根本上避免蒸发过程中的结垢问题.针对于非接触式蒸发结构相对复杂、缺乏有效预测模型的问题,本文构建了非接触式蒸发结构的稳态热阻网络模型,对于非接触式蒸发结构的蒸发率、吸收-发射器温度以及水表面温度进行了较为准确的预测.基于以上模型进行了非接触式太阳能蒸发的性能分析,得到以下结论:
(1) 在一般情况下的非接触式蒸发中,水体的能量来源包括吸收-发射器辐射传热和空气层传热两部分,计算所得这两部分热量近似相当,分别占比54.2%和45.8%.
(2) 由于在蒸发过程中水位不断下降,空气层厚度增加,这同时对辐射传热和空气传热造成了不利影响,分析显示随着空气层厚度的增加,其两侧的温差增大,吸收-发射器温度上升,水温略微下降,空气传热量下降,辐射传热量略微上升后稍有下降.由于总传热热阻的增大,水面所获得的总热量减少进而导致其蒸发率下降,10 mm空气层厚度下的蒸发率约为4 mm空气层厚度下蒸发率的70%.
(3) 在蒸汽扩散阻力对于非接触式蒸发的影响方面,当蒸汽扩散系数从5×10-6m2/s增大至 2.5×10-5m2/s时,蒸发率提升了2倍,结果显示随着蒸汽扩散阻力的下降,非接触式蒸发结构的蒸发率呈现明显的上升趋势,因此降低蒸汽扩散阻力是提升非接触式蒸发效率的有效途径.

