基于MWSA的热力系统单参数时序预测方法
肖鹏飞, 倪 何, 金家善
(海军工程大学 a. 动力工程学院; b. 船舶与海洋工程学院,武汉 430033)
热力系统具有部件众多、结构复杂和工况多变等特点,设备故障的耦合性强且排故成本高[1].为了提高系统的全寿命健康管理水平,如何通过系统的历史运行参数预测系统未来一段时间内的运行状态,并将得到的预测结果作为系统运行管理策略和装备维修的参考,已成为当前热力系统科学管理的重要研究方向之一[2-3].
热力系统的运行参数大多为非平稳时间序列.在非平稳时间序列趋势项的提取方面,文献[4]对风速时序数据进行预测并基于排列熵(PE)的经验模态分解(EMD)趋势项提取算法,结合人工神经网络(ANN)的预测模型对提取的趋势进行预测,通过计算预测数据与实际数据的相关系数来验证预测精度,相比未引入排列熵算法的EMD结合ANN的EMD-ANN算法具有更好的预测效果;陈亮等[5]提出基于集合经验模态分解(EEMD)和奇异值分解(SVD)的排列熵非平稳时序趋势提取方法,并通过与文献[6]和文献[7]中的方法进行对比,验证了该算法的优越性,但由于EEMD分解后的各个本征模态函数(IMF)含噪信息不一,且在分解后的噪声分量和信号分量的分界问题方面选择直接去掉最高频分量的方法而未做量化分析,导致最高频IMF分量中的信号信息丢失,其余分量未进行降噪处理,使后续趋势提取误差增加;刘海江等[8]提出利用EMD结合小波阈值去噪(WTD)的降噪方法,在保留原信号信息的基础上对噪声进行了更有效地消除,但因EMD算法中的“端点效应”问题导致重构信号误差较大;黄礼敏[9]在EMD算法的基础上提出了中值回归经验模态分解(MREMD)方法,有效解决了EMD分解过程中的“端点效应”问题,并且优化了包络线生成方式,但同样未对分解后的IMF分量进行定量分界,导致后续计算结果误差较大.Behera等[10]利用整合滑动平均自回归(ARIMA)模型,通过对公共部门每天接到的电话次数进行预测,并与实际数据对比分析,验证了模型的有效性,其预测结果可作为部门管理层规划员工日常工作量的参考.但由于热力系统中的参数历史数据中包含较多干扰,直接采用ARIMA模型预测误差较大;仇琦等[11]在ARIMA预测模型的基础上提出了基于EMD结合ARIMA的EMD-ARIMA算法预测模型,通过对光电功率信号经EMD分解后的预测验证了模型的有效性,但这两种方法都未对原始非平稳信号的趋势进行提取,导致预测干扰较大.
基于上述研究提出一种热力系统单参数时序预测模型,由MREMD、WTD、基于奇异值分解和排列熵的K-means聚类算法(SVD-PE-KCA)和ARIMA共4部分组成,简称MWSA.利用对原始信号的分解、降噪和趋势提取,使预测结果更加精确,可为热力系统的运行管理、控制优化和维修保障研究提供底层输入,具有一定的理论创新和工程应用价值.
1 预测步骤和算法
基于MWSA的单参数时序预测流程如图1所示.
首先,利用MREMD算法将历史运行参数的时序数据信号分解为若干个IMF分量和1个残余分量(Rn);其次,计算各个IMF分量与原信号的互相关系数和均方根误差,筛选出不符合阈值条件的分量进行WTD,并将去噪后的IMF分量与原本符合筛选条件的分量以及残余分量重组成新的IMF分量;再次,利用SVD将重组后的新IMF分量分解,重构成按照奇异值升序排列的奇异值分量,并采用基于优化参数的PE算法计算各个IMF分量的熵值,利用K-means聚类算法针对各IMF分量熵值进行分类;最后,选取熵值较低的一类IMF分量重构为当前运行参数的变化趋势项,并采用ARIMA模型对其进行预测.
1.1 MREMD分解
MREMD采用自回归(AR)模型对信号端点延拓,并用优化包络线拟合的方法改善了EMD算法中的“端点效应”问题,具体步骤和算法如下.
步骤一对于长度为N的初始时间序列x0(t),采用如下式所示的p阶AR模型对x(t)的左右端点进行预测延拓,即x(t)为延拓后的新序列,使左右端点处于延拓后时间序列的相邻两个极值点之间.
xt=φ0+φ1xt-1+φ2xt-2+…+φpxt-p+μt
(1)
式中:xt(t=p+1,p+2, …,N)为均值点;φ0,φ1,…,φp为p+1个实数;μt为零均值的白噪声序列.
h1,0(t)=x0(t)-m1,0(t)
(2)
步骤三将计算得到的信号分量h1,0(t)作为原始信号,重复步骤一和步骤二进行迭代计算,直到经过l次迭代后的信号分量h1,l(t)满足如下式所示的终止条件.
(3)


z=1, 2, …,k+1}≥68.5%
(4)
(5)

步骤四将h1,l(t)作为1阶本征模态函数(即I1分量)输出,x0(t)-I1得到分量R1,并将R1作为原始信号重复步骤一至步骤四,直到残余信号成为单调函数或分离不出新的IMF分量为止,残余信号提取过程表示为
(6)
式中:下标n为能够分解出的IMF分量个数.
经过上述分解后,原始信号x0(t)可表示为所有IMF分量和最终残余分量之和,表达式为
(7)
1.2 IMF分量选取
对于MREMD分解后的IMF分量,噪声主要集中在高频分量中,在工程实际应用时一般通过舍弃高频分量的方法来达到降噪的目的,但这同样也会丢弃部分的信号信息,使得分析结果产生误差.此外,虽然低频分量通常包含了较多的信息成分,但同样也存在一些噪声,仅靠舍弃高频分量的方法并不能够实现完全降噪的目的.为此,本文采用王彬蓉等[13]提出的IMF分量筛选方法对所有分量进行筛选,在降噪的同时尽可能多地保留原始信号的信息,具体步骤和算法如下.
步骤一计算各阶IMF分量与原始信号的相关系数ci和均方根误差RMSEi,表达式为
(8)
(i=1, 2, …,n)
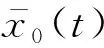
步骤二计算IMF分量相关系数筛选阈值和均方差筛选阈值,表达式为
(9)
步骤三选取满足如下条件的IMF分量,进行小波阈值降噪为
ci≤λIMF, RMSEi≥δIMF
(10)
1.3 WTD
WTD是利用小波变换将原始信号分解成多层近似系数和细节系数,由于经过小波变换后的噪声信息主要集中在绝对值较小的细节系数中,所以可通过将绝对值小于规定阈值的细节系数设置为0,并将剩余小波系数(即分解得到的近似系数和保留的细节系数)通过小波逆变换重构回原始信号的方法,以达到去除噪声的目的,具体步骤和算法如下.
步骤一阈值选取.传统WTD的阈值选取方法有固定阈值法、自适应阈值法、启发式阈值法和极大极小阈值法等[14].本文采用改进的固定阈值法,通过细节系数对每一层的噪声进行估计,同时利用系数ln(j+1)逐层降低细节系数的阈值[15],从而尽可能多地保留蕴含在高频分量中的真实信号,其阈值选取准则为
(11)
式中:λj为第j层小波细节系数的噪声阈值;d(j)为第j层小波细节系数;median为中间值函数,即将每层系数按照降序排列后,取其中间数的值(当系数个数为奇数时)或中间两个数的均值(当系数个数为偶数时).
步骤二阈值处理.常用阈值处理函数有硬阈值函数、软阈值函数和复合阈值函数[16]等,依次表示为
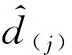
1.4 趋势项提取
采用SVD、PE和K-means聚类算法的组合以实现信号的进一步降噪和趋势项的提取,具体步骤和算法如下.
步骤一SVD分解.将经过小波阈值降噪处理后的n个IMF分量I1~In和残余分量Rn去均值,然后以列向量的形式组成矩阵AN×(n+1),并计算其协方差矩阵B(n+1)×(n+1):
AN×(n+1)=
(12)
(13)
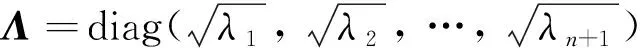
将矩阵U和A中0特征值所对应的向量去掉,重构后的K个奇异值分量表示为
IN×K=AN×KUK×K=(P1P2…PK)
(14)
式中:PK为第K个奇异值分量.
步骤二PE计算.利用延迟相空间重构法[17]对IN×K中各个奇异值分量进行重构,如对分量P1重构表示为
(15)
式中:l=N-(m-1)τ;p1, i(i=1, 2, …,N)为第1个奇异值分量的第i个元素;m为嵌入维数;τ为延迟时间.
将重构矩阵的每行元素按升序排列,得到每行元素的索引值,然后将每行元素的索引值组成索引向量并构成索引矩阵.索引矩阵中每行元素的排列方式共有m!种可能,假设第b种排列方式在索引矩阵中的出现次数为ub,统计其出现的频率为
fb=ub/m!,b∈(1,K)
(16)
由式(16)可计算得到各奇异值分量的排列熵为
(17)
步骤三K-means聚类.根据计算得到的排列熵值对IMF分量进行聚类,选取熵值较低的分量重构原始信号的趋势项.首先,任意选取其中1个点ρ1作为1个类别中心,并选择与ρ1距离最远的ρ2点为另1个类别中心,计算熵值序列中其余对象点x与ρ1和ρ2的距离为
d(ρ,x)=|x-ρ|
(18)
然后,把其余各点划分到与两个类别中心距离近的一类,将两类点的均值作为新的类别中心进行分类,重复上述步骤,直至两个类别中心不再发生变化为止.最后,将两类熵值点中平均熵值较低一类所对应的奇异值分量筛选出来[18],重构为原始信号的趋势项为
(19)
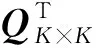
1.5 ARIMA预测模型
ARIMA常用于差分平稳时间序列的拟合和预测,具体步骤和算法如下.
步骤一对式(19)计算得到的趋势项TN×1进行平稳性(Phillips-Perron)检验[19],然后对检验结果为非平稳的时间序列作差分平稳化处理,表示为
(20)


(21)

步骤三经过AIC检验得到模型的自回归系数多项式阶数s和移动平均系数多项式阶数q,并拟合ARIMA(s,d,q)模型表达为
yt=c+a1yt-1+…+asyt-s+εt-
b1εt-1-…-bqεt-q
(22)

步骤四对ARIMA模型的残差序列进行LB(Ljung-Box)统计量检验[21],表示为
(23)
∀k′>0

2 预测案例
以某型船舶蒸汽动力系统的除氧器水位为案例,对上述基于MWSA的热力系统单参数时序预测方法进行验证.按1.1节的步骤和算法,对一段时间内监控系统采集的实际水位数据进行MREMD分解,得到7个IMF分量和1个残余分量,如图2所示.
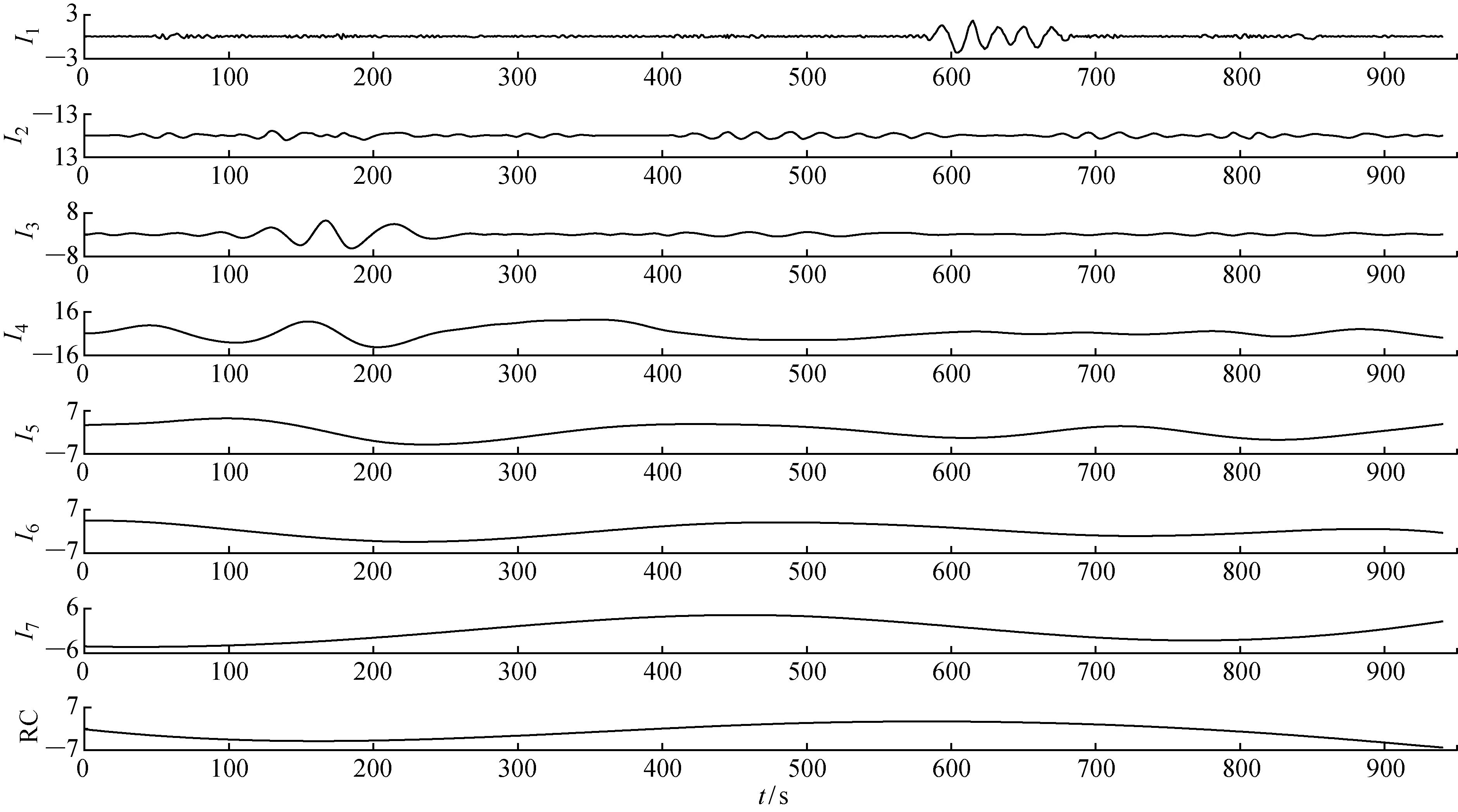
图2 分解得到的IMF分量和RCFig.2 Decomposed IMF component and RC
对于分解得到的分量,根据式(8)计算其与原始信号的相关系数和均方根误差,如表1所示.
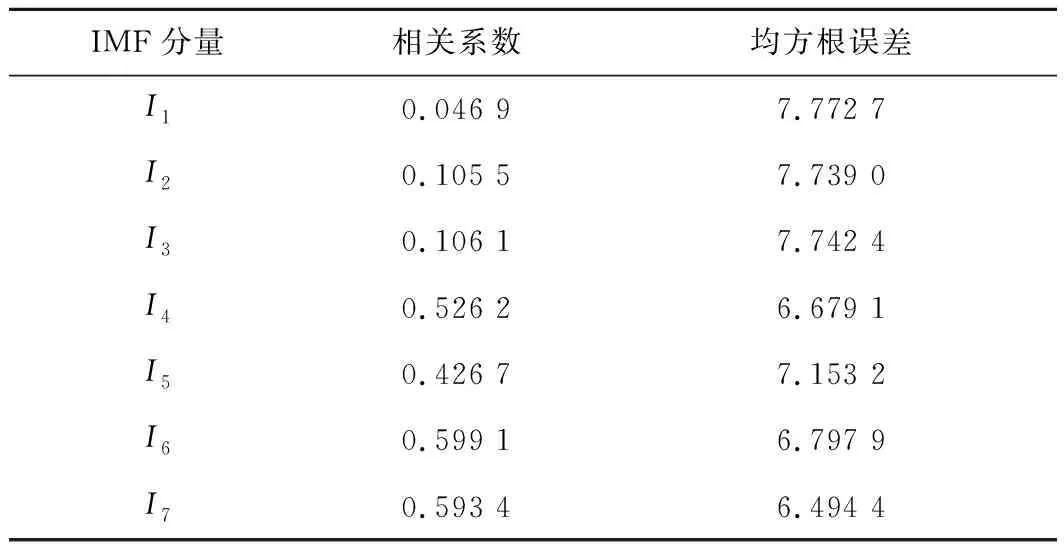
表1 各个IMF分量与原信号的相关系数和均方根误差Tab.1 Correlation coefficient and root mean square error of each IMF component relative to the original signal
根据式(9)计算得到IMF分量相关系数的筛选阈值λIMF=0.301 7,均方差的筛选阈值δIMF=7.314 1,符合条件的分量有I4~I7.按1.3节的具体步骤和算法对I1~I3进行小波阈值降噪,经反复测试,选取Sym4小波基,分解层数为3层.采用固定阈值选取方法,根据式(11)计算各层的噪声阈值.采用不同阈值函数处理后的各IMF分量的信噪比及均方根误差,如表2所示.

表2 去噪后各IMF分量的信噪比、均方根误差Tab.2 Signal-to-noise ratio and root mean square error of each IMF component after denoising
由表2可知,对于高频的I1分量,采用复合阈值降噪的信噪比更高,均方差更小.但对于较低频的I2和I3分量,采用硬阈值降噪的效果更佳.按1.4节的步骤和算法,将降噪后的I1~I3与I4~I7及残余分量Rn一起进行SVD分解,得到8个奇异值分量即P1~P8,如图3所示.
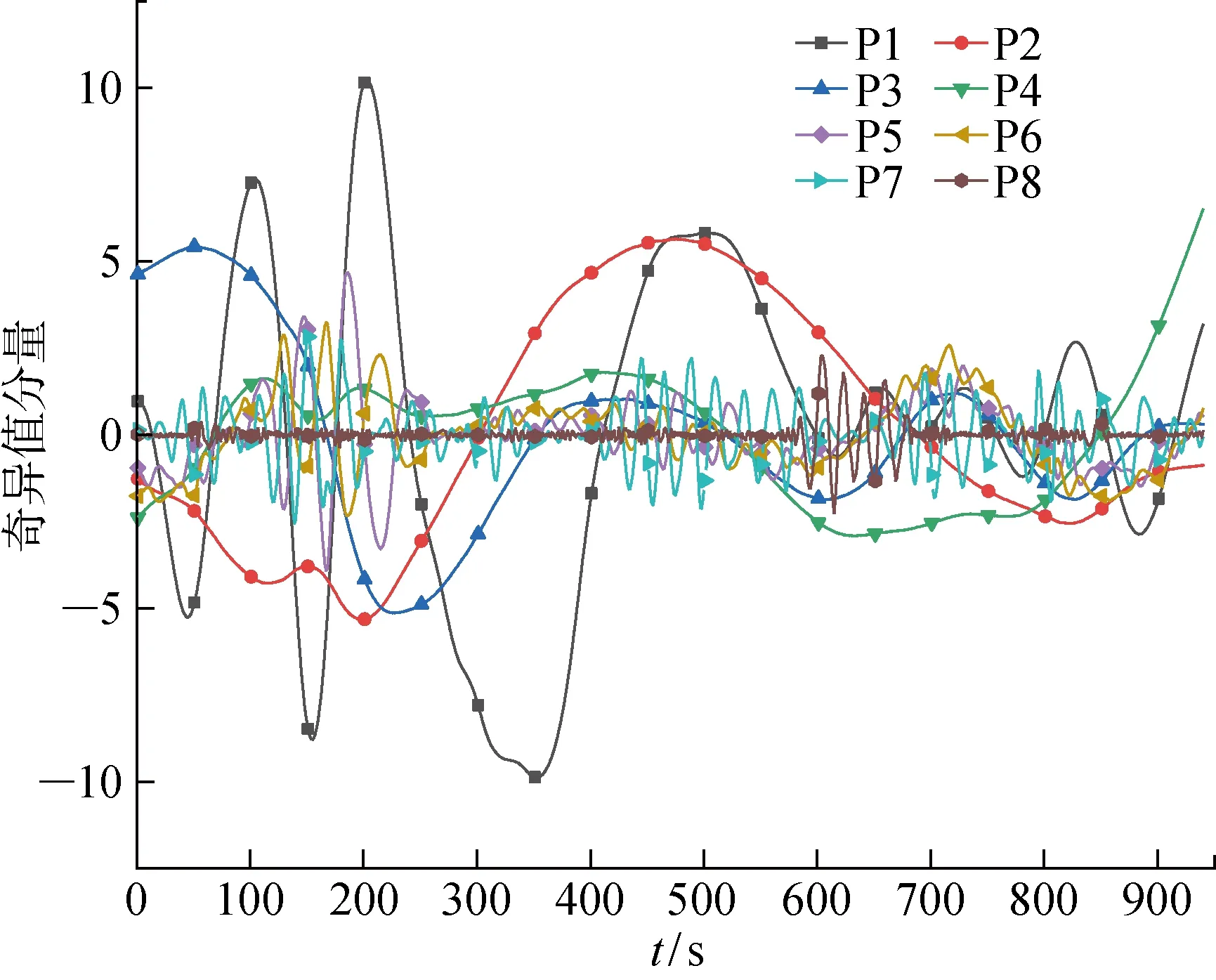
图3 SVD分解后的奇异值分量Fig.3 Singular value components after SVD decomposition
根据式(15)~(17)计算各奇异值分量的排列熵值.在相空间重构时,运用互信息法[22]选取最佳延迟时间,在1~100 s的延迟时间范围内,各奇异值分量的互信息值Mi1~Mi8变化如图4所示.采用伪近邻法[23]计算最佳嵌入维数,在1~10的嵌入维数变化范围内,各奇异值分量的伪近邻率FNNP1~FNNP8随嵌入维数m的变化如图5所示.

图4 各分量互信息值随延迟时间的变化曲线Fig.4 Variation curve of mutual information value with delay time

图5 各分量伪近邻率随嵌入维数的变化曲线Fig.5 Variation of pseudo nearest neighbor rate with embedding dimension
取图4中互信息值随时间变化曲线的第一个极值点为各奇异值分量的最佳延迟时间τopt;取图5中伪近邻率小于5%时的嵌入维数为各奇异值分量的最佳嵌入维数mopt;然后将其代入式(15),并通过式(16)和式(17)计算得到各分量的排列熵值,如表3所示.

表3 各奇异值分量的最佳延迟时间、最佳嵌入维数和排列熵值Tab.3 Optimal delay time, embedding dimension, and permutation entropy of each singular value component
对各分量的排列熵值进行K-means聚类,选取P2、P3和P4共3个分量进行趋势项重构,结果如图6所示.
根据1.5节的步骤和算法,对除氧器水位进行拟合和预测.首先,对如图6所示的趋势项进行Phillips-Perron检验,结果为非平稳序列,再经过4次差分计算后转换为平稳序列;然后,对差分平稳化后的序列进行AIC,得到自回归系数多项式阶数s以及移动平均系数多项式阶数q分别为1和3;在经过4次反差分计算和LB统计量检验后,拟合得到如式(22)所示的ARIMA(1, 4, 3)模型.
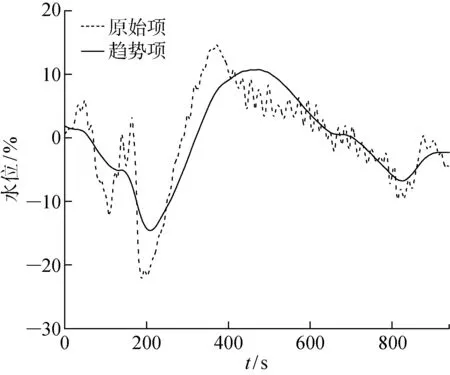
图6 除氧器水位的原始项与趋势项Fig.6 Original item and trend item of deaerator water level
取实际运行数据的前90%为训练数据,取后10%为检验数据,预测除氧器水位在未来94 s的变化趋势,结果如图7所示.而在相同数据输入下,采用文献[23]中提出的无降噪处理的算法(MSOP)得到的预测结果如图8所示.
由图7和图8 可知,随着预测时长的增加,两种方法的预测误差都会增大.经计算,在采用MWSA方法时,预测结果与实际数据(检验数据)的均方差为1.388 7;而文献[23]中提出的方法其预测结果与实际数据(检验数据)的均方差为2.133 4.可知,本文预测方法的准确度更高.
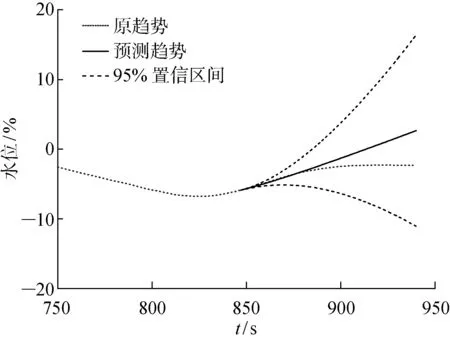
图7 基于MOSP的除氧器水位趋势项与预测项Fig.7 Trend and prediction of deaerator water level based on MSOP

图8 基于MWSA的除氧器水位的趋势项与预测项Fig.8 Trend and prediction of deaerator water level based on MWSA
3 结语
提出一种基于MWSA的热力系统单参数时序预测方法,并以某型号船舶蒸汽动力系统的除氧器水位为例,根据实际运行数据预测其在未来一段时间内的变化趋势.通过与基于MSOP的时序预测方法对比,证明所提方法的预测误差较小,预测结果较为准确.该算法完全基于基本物理规律,利用纯数学推导得出,在推导过程中未加入任何约束条件或有关具体设备的辅助方程,在数学上具有本质的普适性.利用滑动数据采集窗口可以对其他时段的数据进行分析验证,亦可通过添加其他设备的数据接口,对其他热力参数进行分析和预测.研究成果可用于热力系统的运行管理、控制优化和维修保障研究,达到优化运行管理和控制策略,合理安排维修保障资源、减少设备故障和延长系统使用寿命的目的.

