采用叠片法的黄铜低温接触热阻测量
沈 逸, 曹家兴, 黄永华
(1. 上海交通大学 制冷与低温工程研究所,上海 200240; 2. 上海精密计量测试研究所, 上海 201109)
接触热阻是航空航天、机械制造、低温超导、精密电子等众多领域广泛涉及的物理现象——当两个固体接触时,表面粗糙度使得实际接触面积远小于理论接触面积;法向热流仅能通过实际接触点传导,从而在接触界面上产生温度的突变.接触热阻的存在将会导致诸多工程问题:高功率微电子器件的散热面临巨大挑战;低温下超导材料因温度阶跃产生失超;小型低温制冷机冷头的制冷量及极限温度无法发挥等.因此,掌握典型固体接触热阻数据及其特性十分必要.
对于接触热阻的研究,通常从理论模型预测和实验测量两方面进行,本文主要关注实验测量.以往的测试方法主要分为瞬态法和稳态法.瞬态法具有测量时间短、样品尺寸要求低等特点.目前主流的接触热阻瞬态测量法包括光声法[1-2]、光热法[3-4]、闪光法[5]、热成像法[6]、平面热源法[7]等.随着纳米技术和相应尺度测量技术的飞速发展,也出现3ω法[8]和瞬态热反射法[9]等适合微尺度接触热阻的测量方法.如Chen等[10]采用红外热成像法研究630~1 100 K 高温下0.1~0.6 MPa压力内碳纤维增强二硼化锆/碳化硅基复合材料间的接触热阻变化规律.Bi等[11]采用瞬态非接触激光光热法测量温度为70~290 K,压力为0.2~0.7 MPa条件下铜、不锈钢以及氮化铝等材料之间的接触热阻,分析温度和接触压力对界面接触热阻的影响,给出一定压力下接触热阻和温度的关系.彭小方等[12]采用激光光热法测量3.0 kPa~0.32 MPa压力以及20~120 K温度内紫铜-紫铜界面接触热阻,并从微观角度对变化规律进行机理分析.
稳态法测量接触热阻虽然测量时间较长、对测试样品的尺寸要求较高,且在低温环境下不可避免地存在传感器引线漏热和辐射漏热,但它也具有实现和操作简单、精度较高等优点.应济等[13]采用稳态法设计接触热阻测量装置并在常温下进行实验测量,测量结果和理论计算结果吻合良好.刘菊[14]研制了一套测量接触热阻的实验装置,利用两层法和三层法测量黄铜材料在305 K的热导率,并研究界面载荷、加热功率和温度补偿对接触热阻的影响.韩雪峰[15]依据稳态法测量原理设计了一套测量接触热阻的实验装置,分析认为系统的测量误差主要来源于热电偶的固有误差和辐射交换引起的误差.王安良等[16]提出测量接触热阻的新方法“叠片法”,方便测量的同时还可以提高测量精度.针对低温温区的稳态测量主要集中在液氮温区附近及以上.Yu等[17]测量了铜-铜和铜-硅界面在85~300 K之间的热导率,评估了裸露表面和涂有导热硅脂表面的接触热导.徐烈等[18]用双热流法测量液氮真空环境下紫铜、铝以及不锈钢固体界面在168~218 K之间的接触热阻.Kumar等[19]测量了50~300 K温区内不锈钢和铝两种材料接触热阻随温度的变化情况.Xu等[20]测量了155~210 K低温条件下5052铝合金和304不锈钢的接触热导,并引入分形维数概念对粗糙表面进行表征.
综上所述,国内外学者已经对紫铜、铝合金、不锈钢等多种材料的接触热阻进行了一定的测量研究,但鲜有液氮温度以下极低温的实验数据,且对低温下常用的材料黄铜研究较少.本文基于以稳态法为基础的叠片法,以二级G-M低温制冷机为冷源研制一套实验装置,针对黄铜材料测量10~30 K温区内不同温度和压力下的接触热阻,并借此研究温度、压力、界面粗糙度等不同因素对低温接触热阻的影响规律.
1 稳态叠片法测量原理
稳态法通常基于傅里叶一维传热定律,即通过直接将样品接触,测量上下试样内的温度分布及热流,拟合外推得到接触面温度阶跃,从而计算接触热阻,如图1(a)所示.上下两段为待测固体样品,其上均匀分布若干小孔用于放置温度传感器,中间为接触界面,在此处产生温度阶跃.界面接触热阻为
(1)
(2)
式中:Rc为中间界面接触热阻;ΔTi为界面温差;q为轴向热流密度;k为上下样品的热导率;dT/dx为上下样品内的温度梯度,T为样品温度,x为样品热流方向上的坐标.因此,仅需测量上下样品内各点温度即可计算接触界面热阻.需要指出的是,当被测材料热导率较大时,该方法通常面临着上下试样温度梯度不明显、接触面温度阶跃小难以测量、样品制作用料多等问题,影响测量精度的同时增加成本.
采用稳态叠片法以提高测量精度,其特点在于上下两段改用热导率较小的材料制成工装,将待测固体样品制成扁平圆柱状置于两段工装之间,从而达到增大温度梯度、减小测量误差的效果,如图1(b)所示.图中:Rbs1为工装与样品1界面接触热阻;R1和R2分别为样品1、2材料自身热阻;Rbb为两个样品之间的接触热阻;Rbs2为样品2和不锈钢工装之间的接触热阻.采用304不锈钢作为上下热流计工装,轴向均匀布置多个直径1 mm钻孔作为测温点,顶部布置加热器提供稳定热流,底部连接G-M制冷机二级冷头.由于样品为某一特定材料,所以认为R1=R2=Rb,Rbs1=Rbs2=Rbs.当中间放置n块待测样品时,所有样品的总热阻为
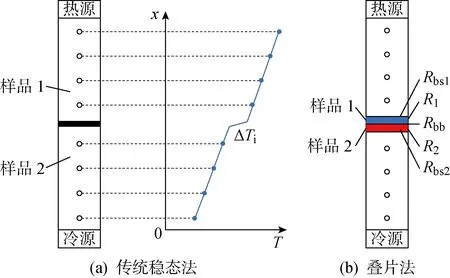
图1 稳态法测量接触热阻原理Fig.1 Principle of steady state method for measuring thermal contact resistance
Rn,tot=nRb+(n-1)Rbb+2Rbs
(3)
式中:Rb为待测样品本身热阻;Rbs为样品与工装之间接触热阻.1次测量完成后,再增加(或减少)1块待测样品进行第2次测量,控制压力和样品温度不变,即保持样品自身热阻、样品之间以及样品和不锈钢工装之间的接触热阻不变,此时总热阻为
Rn+1,tot=(n+1)Rb+nRbb+2Rbs
(4)
通过将两次测量的总热阻Rn+1,tot和Rn,tot求差值,便可以计算出待测样品间的接触热阻:
Rbb=Rn+1,tot-Rn,tot-Rb
(5)
其中样品自身热阻为
(6)
式中:h为样品厚度.一般固体材料的热导率均会随
温度产生变化,对于黄铜可通过下式[21]计算,即
lgk=a+blgT+c(lgT)2+
d(lgT)3+e(lgT)4+f(lgT)5+
g(lgT)6+i(lgT)7+j(lgT)8
(7)
式中:a,b,c,d,e,f,g,i,j为方程系数.可见,叠片法虽然需要通过两次测量才能得出结果,相对传统稳态法而言稍微繁琐,但其具有以下几个优点:① 上下工装热导率小,温度梯度明显,便于准确测量和拟合外推;② 中间温度阶跃大,对传感器精度要求降低;③ 待测样品制作简单,无需安装温度计,更换方便.与此同时,该方法也有其适用条件:① 由于需要通过多次测量取差值以消除工件与样品之间的接触热阻,该过程中假定不同样品和工件的接触热阻值保持不变,所以准备样品时需要尽可能保持同种样品的界面粗糙度基本一致;② 热流在自上而下传递的过程中,不可避免地会产生一定量损失,因此样品的厚度不宜过大,块数也不宜过多;③ 测量样品的热导率不宜过大,否则难以在样品两端建立足够大的温差,引起计算误差增大甚至测量失效.同时,用作热流计的上下工件材料热导率也不宜过大,否则难以建立足够的温度梯度(受限于温度测量精度)来计算热流.
2 实验方案设计
实验系统如图2所示,主要由测试段、二级G-M制冷机、真空腔体、机械泵/分子泵、温控仪、数据采集仪、冰点仪、加热和传感元件以及数据采集程序组成.实验所用制冷机为日本住友重机械工业株式会社生产的RDK-408D2型二级G-M制冷机,其一级冷头在制冷温度43 K下的制冷量约为40 W;二级冷头在4.2 K制冷温度下约有1 W制冷量,极限制冷温度低于2.6 K.实验时,接触热阻测试部件(测试段)固定于二级冷头上,一级冷头用于为辐射冷屏提供冷量.相关设备部件型号和参数见表1,表中空白表示无此项.
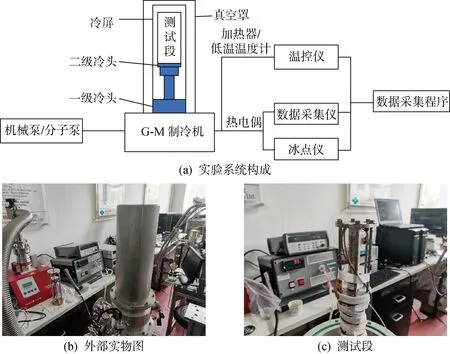
图2 实验系统构成和实物图Fig.2 Schematic and physical image of experimental system

表1 主要设备部件型号及参数Tab.1 Main equipment and devices
测试段主体由304不锈钢制作,每段高50 mm,直径为20 mm,其上均匀分布4个直径为1 mm、深10 mm 的圆形钻孔,用于放置热电偶,并填入适量的纳米含银硅脂用于增强导热.待测样品为直径 20 mm、厚5 mm的圆形黄铜块,共有Ra1.6、Ra3.2和Ra6.3这3种粗糙度,如图3所示.样品委托专业生产商使用车床切削加工而成.图4为样品经过原子力显微镜放大后的高清拍摄照片,可以通过纹理的疏密程度清晰地分辨出3种粗糙度.工装和样品通过6根螺杆固定于二级冷头上,并通过扭力扳手调整螺栓转矩达到控制压力的作用.温度传感器采用标定过的T型热电偶.使用Lake Shore Cernox温度计配合335温控仪对热端进行控温.同时,在一级冷头上加装防辐屏,用来减小辐射漏热.Keysight 34972A数据采集仪实时采集并记录热电偶感应电势(经冰点仪零度补偿),之后通过分度表插值转换为对应温度值.

图3 3种粗糙度的黄铜样品Fig.3 Brass samples with three kinds of roughnesses

图4 样品扫描图Fig.4 Sample scanning
本文主要针对温度、螺栓转矩(M)以及接触面粗糙度3种影响因素进行研究,具体实验工况如表2所示.某一工况下的数据采集面板如图5所示.图中:Pr为相对加热功率;Tc和Th分别为冷端温度和热端温度;Ts为温控仪设置的热端控温温度,基本和Th(即实测温度)重合.该实验系统从常温降温至极限温度4 K所需时间(t)约3.5 h,之后对其进行控温.每一个控温点在功率稳定后保持30 min,达到稳态,其判断依据如下:

图5 不同工况下的温度控制Fig.5 Temperature control in a certain working condition

表2 黄铜样品实验工况Tab.2 Experimental conditions of brass samples
(1) 通过采集和计算一段较长时间内热电偶感应电势的标准差,来判断测试段温度分布是否达到稳态.如图6所示,以30 K工况下1号和6号两个电偶的感应电势(U)在 2 500 s 内的变化情况为例,利用Excel自带的标准差计算公式可以计算得到这两个热电偶感应电势在这段时间内的标准差分别仅为2.77×10-7和3.01×10-7,相对于测量值非常小,可以认为已经达到稳态.
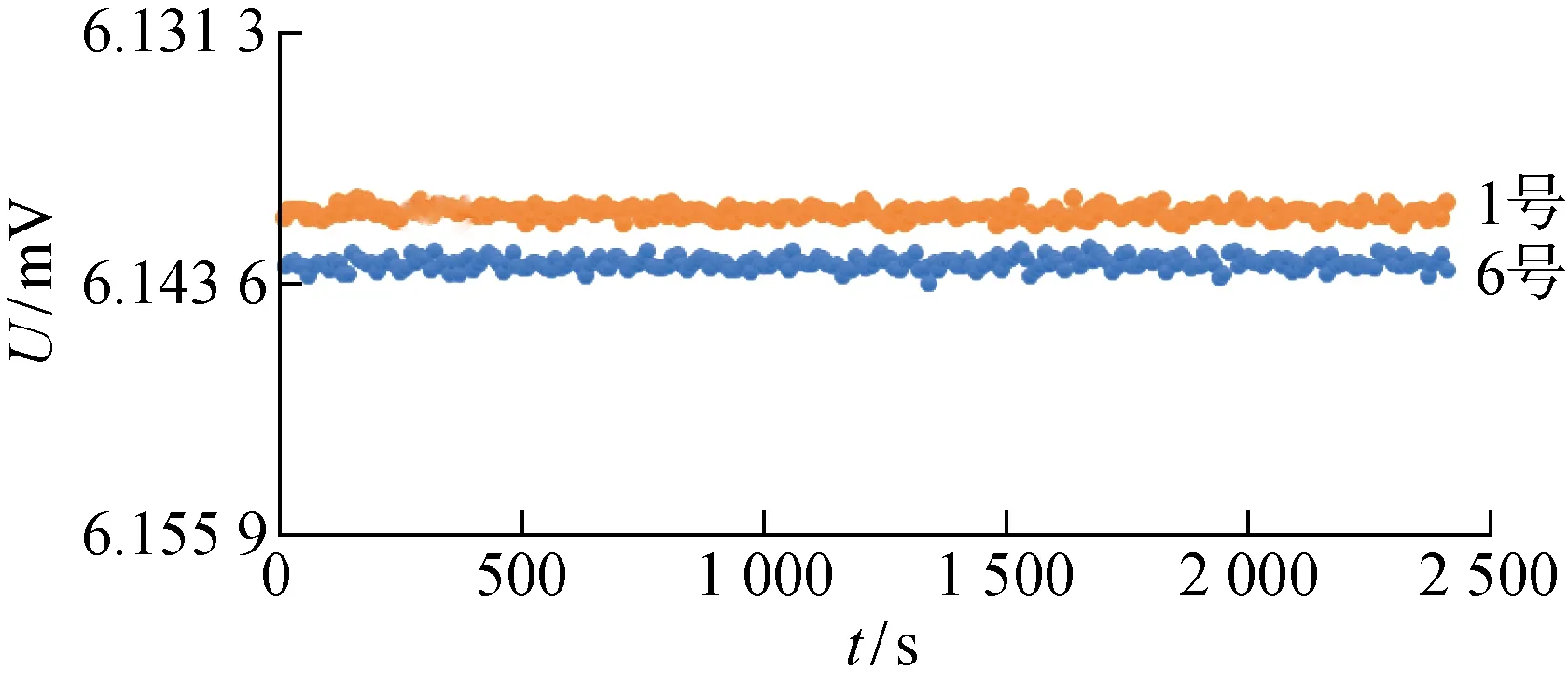
图6 T=30 K时1号和6号热电偶感应电势变化情况Fig.6 Electric potential of No. 1 and No. 6 thermocouple versus time at T=30 K
(2) 从图5所示的显示面板上加热功率、热端温度以及冷端温度曲线的平台也可辅助判断.
3 结果与分析
每次实验的待测样品和接触面总热阻可以通过对原始温度数据进行拟合并外插值计算得到.某一工况下的拟合外推曲线如图7所示,离散数据点为实测温度点和外推获得的样品上下界面推测温度点,实线为拟合直线,虚线为样品接触面的温度跳跃.从图中可以得到以下信息:① 上下两段不锈钢工件上的轴向温度分布基本呈线性,这是因为在一个比较小的温度范围内,不锈钢的热导率变化并不明显或者基本呈线性微量变化;实验腔体内真空度高,且有铜冷屏防辐射进一步减小径向热流损失,使得热流基本沿轴向传递;② 样品两端确实建立足够明显的温差,从而降低对测温精度的要求;③ 低温区拟合曲线斜率略大于高温区拟合曲线,意味着温度越低,热导率越小,符合不锈钢工件热导率随温度升高而增大的特性.根据傅里叶传热定律:q=-kdT/dx,假定热流密度恒定,理论上上、下两段拟合直线的斜率Kh和Kl之比应为对应段热导率kh和kl之比的倒数,即

图7 M=0.8 N·m和Th= 30 K工况下某样品的拟合外推曲线Fig.7 Fitting extrapolation curve at M=0.8 N·m and Th=30 K for one sample
(8)
根据NIST数据库304不锈钢材料的热物性数据,可以计算出图中对应的kl约为1.9 W/(m·K),kh约为2.8 W/(m·K),则kl/kh≈0.68,而图中斜率之比Kh/Kl≈0.74,差距约为8.1%,这一数据不是本实验装置的测量精度,但能够说明测量方法的合理性.
根据上述拟合外推曲线,即可得到样品两端温差,进而计算得到各工况下的样品和接触面总热阻.对螺栓转矩和控温相同,但样品块数不同的两组总热阻取差值,即可获得该螺栓转矩和控温下对应的黄铜块之间接触热阻.测量数据显示,在10~30 K温度、0.8~1.4 N·m螺栓转矩内,黄铜接触界面的接触热阻值大约位于6.89×10-4~1.86×10-2m2·W/K之间,跨度较大.下面将选取部分工况对各种因素的影响一一进行分析.
图8给出粗糙度Ra3.2,螺栓转矩为1.0和1.4 N·m时接触热阻随温度的变化曲线(部分点已隐去),其中散点为各工况下接触热阻的测量值,曲线为光滑拟合后的结果.由图可见,在1.0~1.4 N·m 的螺栓转矩以及15~30 K的温区内,Ra3.2 粗糙度的黄铜接触面接触热阻值大约在1.07×10-3~1.16×10-2m2·W/K之间,转矩越大,接触热阻越小.在相同螺栓转矩下,接触热阻始终随着温度的升高而减小.这是因为在低温真空环境下,固体材料间的接触热阻主要和材料自身导热系数、硬度、弹性模量等物理性质相关.随着温度升高,黄铜的导热系数增大,同时硬度和弹性模量减小,样品自身也会产生一定热膨胀,使得实际接触面积增大,在两者的共同作用下,接触热阻显著减小.对于不同螺栓转矩,接触热阻和温度之间基本呈现相同的变化趋势,其特点是随着温度不断升高,接触热阻减小速率将会越来越小,主要有两个原因:一是因为黄铜的导热系数在低温下变化显著,但随着温度升高,其上升趋势减缓;二是温度升高导致的实际接触面积增大幅度也会逐渐减小.
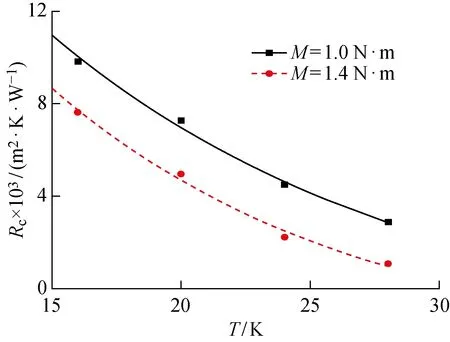
图8 Ra 3.2,不同螺栓转矩下接触热阻随温度变化曲线Fig.8 Rc versus temperature at Ra 3.2 and different preloads
图9给出1 N·m螺栓转矩时,Ra1.6和Ra3.2粗糙度下接触热阻随温度的变化情况.在给定的粗糙度下,黄铜样品接触热阻均随温度升高而减小,且变化趋势相近.可以看出,随着粗糙度的增大,接触热阻也相应增大,且变化也较为明显.这是因为粗糙度的增大使得界面实际接触面积减小,固体传热占比减小,等效接触热阻便会相应增大.还可发现,Ra1.6、T=12 K工况下的接触热阻远大于Ra3.2、T=24 K工况,基本达到其2倍左右.粗糙度增大1倍,温度也升高1倍,但接触热阻却减小了1倍,可以认为在低温下温度对接触热阻的影响程度要高于粗糙度,因为在低温真空环境下,固体传热占界面传热的绝大部分,而固体的热导率在低温下有着极强的温度依变关系.同时,在极低温环境下,热胀冷缩可导致接触面压力变小,这也是另一个可能的原因.

图9 M=1.0 N·m, 不同粗糙度下接触热阻随温度变化曲线Fig.9 Rc versus temperature at M=1.0 N·m and different roughnesses
根据所测数据,可以绘制得到三维曲面图,综合表示温度和螺栓转矩对接触热阻的多元作用关系,如图10所示.其整体呈向下弯曲的光滑曲面,显然,除了温度升高外,螺栓转矩的增大也是造成接触热阻减少的另一个重要因素.这是因为转矩的增大直接导致轴向压力的增大,接触界面受到挤压越强,实际接触面积越大.随着转矩的不断增大,减小趋势变缓,这是因为随着实际接触面积越来越大,可供接触面形变的空间也越来越少.虽然接触热阻随转矩的变化和温度相似,但在本文的实验工况范围内,其引起的变化幅度却小于温度.对于同一温度,当转矩从0.8 N·m增大到1.4 N·m (1.75倍)时,接触热阻仅仅减小4×10-3m2·W/K左右;而同一螺栓转矩下,温度从12 K上升到20 K (1.67倍)的过程中,接触热阻减小6.6×10-3m2·W/K左右,是前者的1.65倍.由此可见,在制冷机的实际使用中,尽管温度变化给接触热阻带来的影响是难以避免的,但仍可以选择合适的螺栓转矩,在不损坏冷头的情况下尽量减小接触热阻.以上这些数据可直接用于相关应用涉及的降温时间估算、极限低温估算等.

图10 Ra 3.2下接触热阻随温度和转矩变化曲面Fig.10 Rc versus temperature and torque at Ra 3.2
4 误差分析
所进行的实验主要误差来源如下:① 所使用的T型热电偶测量误差为±0.1 K;② 热电偶插入位置的加工和距离测量,使用游标卡尺,其测量误差为±0.01 mm;③ 黄铜和不锈钢的热导率计算数据误差1.5%;④ 确定等效热导率时,数值方法引入的误差在0.02%左右;⑤ 尽管采取减小热电偶线径,并将热电偶线在热沉上做致密的缠绕处理、加装防辐射屏等措施,但引线漏热和辐射漏热却不可避免.根据上文对不锈钢热导率之比的计算对比,得出漏热引起的热流相对误差在4%左右.
得到上述各种误差数据后,根据误差传递规律,可以计算接触热阻的测量误差.黄铜接触界面热阻的计算公式即式(5).
因此,Rbb的相对误差为
(9)
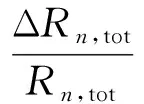
(10)
lnRn,tot=ln(Th-Tc)-lnq
(11)
(12)
(13)
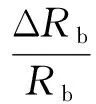
(14)
lnRb=lnh-lnk
(15)
(16)
(17)
代入数据,最终计算得到该方法测量接触热阻的误差约为4.50%~8.75%,属于工程可接受范围.
5 结论
基于RDK-408D2型二级G-M低温制冷机,设计并研制一套低温材料接触热阻测量系统,获得黄铜样品在10~30 K温区的接触热阻,研究温度、粗糙度、螺栓转矩等因素在低温下对接触热阻的影响.得到以下结论:
(1) 采用叠片法能够在上下两段不锈钢工件(热流计)上以及样品两端建立起足够明显的温度梯度/温差,从而相较于传统稳态法大幅提升测量精度,特别是对热导率较高的样品.最终计算得出系统的测量误差在4.50%~8.75%之间.
(2) 在0.8~1.4 N·m螺栓转矩和10~30 K温区内,Ra3.2粗糙度的黄铜接触面接触热阻值在1.07×10-3~1.16×10-2m2·W/K之间.当加入Ra1.6和Ra6.3两个额外粗糙度工况后,接触热阻扩展至6.89×10-4~1.86×10-2m2·W/K.接触热阻始终随温度的升高而减小,随粗糙度的增大而增大,随转矩的增大而减小.在极低温工况下,粗糙度和转矩对接触热阻的影响不及温度显著.

