对抗恶意无人机窃听的无人机通信系统三维航迹规划和功率控制*

苏恭超，代明军，陈 彬，林晓辉，王 晖

(深圳大学 电子与信息工程学院，广东 深圳 518060)

0 引 言

近年来，随着终端数量和数据流量的急速增长，下一代无线通信系统对网络基础架构的灵活性、快速按需服务能力提出了更高的要求，以便为用户提供泛在的实时高速数据传输服务。与传统的地面架设的数据传输设备相比，以无人机(Unmanned Aerial Vehicle,UAV)作为无线网络的数据发送/中继设备可以使得网络快速灵活响应用户的需求，无人机的高移动性使得数据传输不再受到地理位置限制，并且空-地信道不受阴影效应、多径效应等因素的影响，信道质量远高于传统无线网络中的地-地信道。因此无人机通信技术具备巨大潜力，在下一代无线通信网络中受到了广泛的关注[1]。

无人机通信的引入也带来了一些新问题。由于无线信道的广播性质，无线通信容易受到恶意用户的窃听攻击。引入无人机通信技术后随着无线信道的质量提升，窃听者的信道质量也随之提升，无线数据传输面临更加严峻的窃听攻击威胁。为保障无线通信的安全性，物理层安全机制(Physical Layer Security,PLS)得到了广泛的关注[2]。通过利用物理信道的随机性和适当的编码机制，即使攻击者能够攻破传统的加密解密机制来解密用户数据，物理层网络安全机制也能从通信层面为用户数据传输提供绝对的安全保障。因此在无人机协助的无线通信系统中，有必要引入物理层安全机制来应对日益严峻的窃听攻击等挑战[3]。目前已有部分研究关注无人机通信系统中的物理层网络安全机制[4-7]，但这些研究均假设窃听者为地面恶意用户，无人机航迹仅考虑在二维平面空间的飞行路径。文献[8-9]指出相比于二维路径设计，无人机三维路径规划能更有效地提高飞行轨迹的灵活性，从而进一步提升安全通信的性能指标，然而上述研究仍然仅考虑了位置固定的地面窃听者的情况。

另一方面，网络攻击者也能使用无人机对无人机通信系统进行攻击。恶意无人机能够利用其灵活性在空间上靠近合法的无人机传输设备，从而能更有效地窃听用户通信，因此无人机的航迹规划有必要考虑恶意无人机的飞行轨迹而进行相应的设计。文献[10]研究了存在恶意无人机时无人机的二维航迹规划与功率控制，指出通过航迹规划和功率控制尽量避免恶意无人机靠近合法无人机设备，并在接近恶意无人机时降低发送功率，能有效地保障用户安全通信性能，然而该研究未考虑无人机的三维路径规划。

本文研究无人机通信系统中的物理层安全机制，通过对无人机的三维航迹和功率分配进行联合优化，以最大化无人机飞行期间的用户安全通信速率。和已有的研究相比，本文关注空间位置不断变化的恶意无人机对合法无人机三维飞行轨迹设计的影响，在系统模型中同时考虑了无人机的三维航迹控制和恶意无人机的窃听攻击，并将航迹规划和功率控制问题建模为用户安全通信速率最大化问题，在约束条件上充分考虑了三维航迹、功率分配等变量的约束条件，通过迭代优化将该优化问题分解为二维路径、高度控制、功率分配这三个子问题，通过连续凸逼近法(Successive Convex Approximation,SCA)得到近似解，并通过对最优解的分析指出了最优功率分配的显式解。仿真实验表明，无人机三维航迹控制和功率分配能有效应对恶意无人机的窃听攻击，提升用户安全通信性能。

1 系统模型与问题建模

本文考虑如图1所示的无人机通信场景。无人机UAV-S作为用户数据的发送方，需将数据安全传输到某地面用户U处。用户所在位置上方有一恶意无人机UAV-E在按照某种既定轨迹飞行并随时窃听发往该用户的数据。

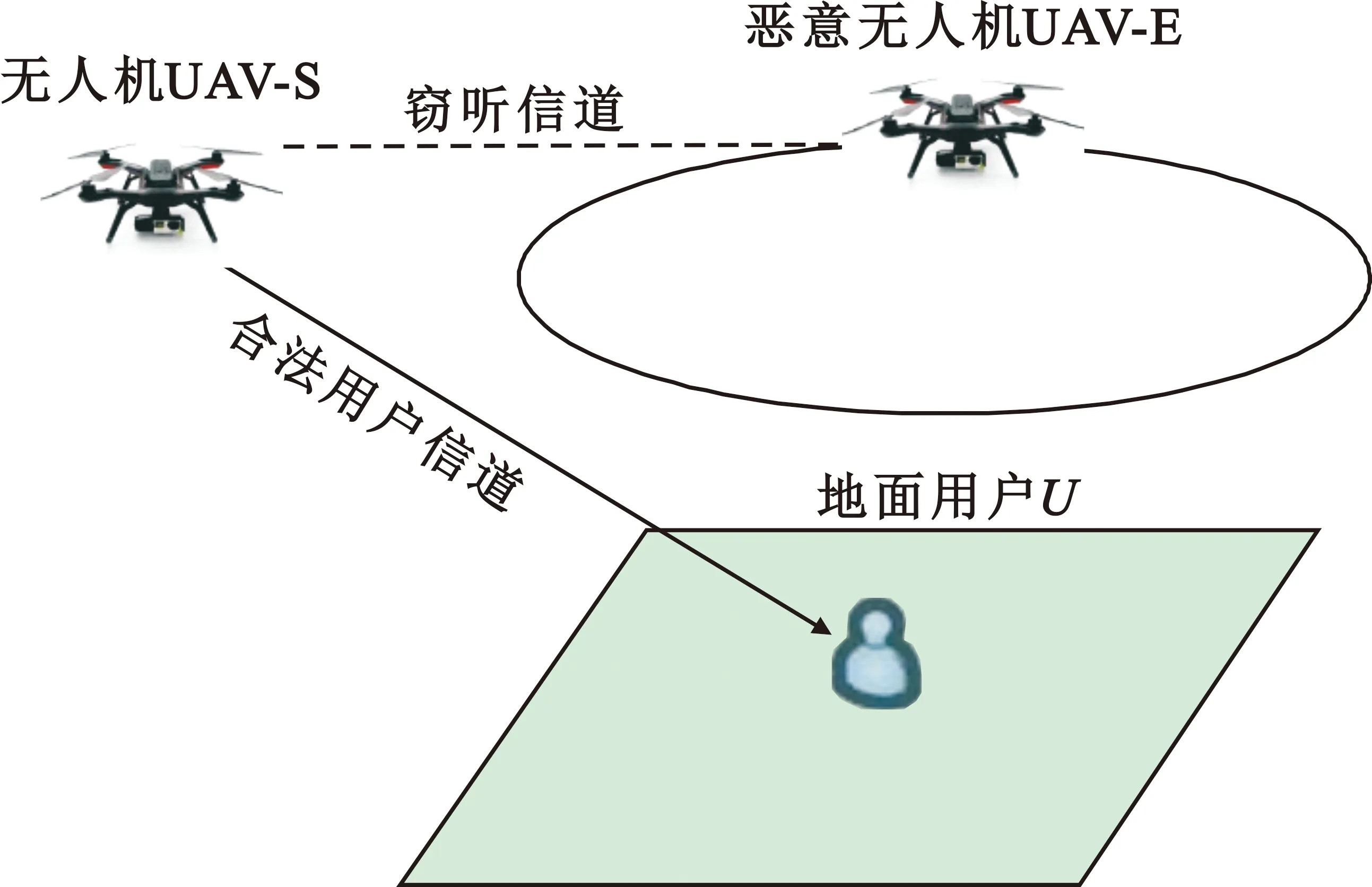
图1 恶意无人机窃听攻击场景

采用笛卡尔坐标系，并假设U位于原点(0,0,0)处，将无人机的飞行时间T分成N个时隙，每个时隙持续Ts秒，因此T=NTs。第n个时隙时无人机UAV-S在三维坐标系下的坐标为(x[n],y[n],z[n])T。令q[n]=(x[n],y[n])T表示x-y平面上的坐标，则无人机在三维空间的位置表示为列向量s[n]=(q[n],z[n])T，q[n]∈2,z[n]∈。无人机起始位置为s0=(q0,z0)T，结束位置sN=(qN,zN)T。无人机的整体飞行轨迹S={s[n]}∈3×N，水平轨迹Q={q[n]}∈2×N，高度z={z[n]}∈N。无人机UAV-S水平方向的飞行速度最大为Vh，垂直方向的最大飞行速度为Vd，最大飞行高度zmax，最小飞行高度zmin。同理定义e[n]=(qe[n],ze[n])T表示第n个时隙时恶意无人机UAV-E的位置，E={e[n]}∈3×N表示UAV-E的整体飞行轨迹。UAV-S的最大发射功率为pmax，令p[n]表示第n个时隙UAV-S的发射功率，向量p={p[n]}表示所有时隙上的功率分配。已有的研究表明，在较为空旷的通信场景如郊区中，在一定高度飞行的无人机，其空地信道主要受路径损耗的影响[11]。因此无人机UAV-S和地面用户U之间的信道以及和恶意无人机UAV-E之间的信道均采用自由空间传播模型[4,6-7]，第n个时隙时UAV-S到U的信道增益hSU[n]以及UAV-S到UAV-E的信道增益hSE[n]分别为

(1)

(2)

式中：‖·‖为向量2-范数；β0为距离为1 m时的信道参考增益。本文设定可以通过地面辅助观测等手段来获得恶意无人机的空间位置和飞行轨迹信息，因此hSU[n]、hSE[n]可成为已知信息。第n个时隙时UAV-S与U之间的数据传输速率(以频谱效率来衡量)为

(3)

式中：σ2为接收方(地面用户和恶意无人机)的噪声功率。UAV-S与UAV-E 之间的窃听信道速率为

(4)

在物理层安全机制下，第n个时隙时UAV-S和U之间的安全通信速率为[12]

Rsec[n]=[RSU[n]-RSE[n]]+。

(5)

式中：[x]+=max(x,0)。定义函数

(6)

以表示整个飞行时间内用户的安全通信平均速率，以该函数为优化目标函数，将最优航迹规划和功率控制问题建模为以下优化问题：

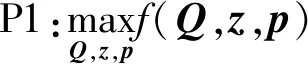
(7a)

s.t.q[1]=q0,q[N]=qN,

(7b)

z[1]=z0,z[N]=zN,

(7c)

‖q[n]-q[n-1]‖2≤VhTs,n=2,3,…,N,

(7d)

|z[n]-z[n-1]|≤VdTs,n=2,3,…,N,

(7e)

0≤p[n]≤pmax,n=1,2,…,N,

(7f)

zmin≤z[n]≤zmax,n=1,2,…,N。

(7g)

约束条件(7b)、(7c)保证无人机S在开始和结束时位于指定位置，(7d)和(7e)保证S在水平方向和垂直方向的速度不超过对应上限，(7f)保证任意时隙时UAV-S的发射功率不超过最大值，(7g)保证UAV-S的飞行高度在指定范围。另外，已有的研究表明，在对安全速率最大化时，可忽略[·]+运算符，得到的优化问题与原优化问题同解[7-8]，因此可以将目标函数改写为

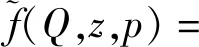
p[n]β0)-lb(‖q[n]‖2+z[n]2)-

lb(σ2(‖q[n]-qe[n]‖2+

(z[n]-ze[n])2)+p[n]β0)+

lb(‖q[n]-qe[n]‖2+(z[n]-ze[n])2))，

(8)

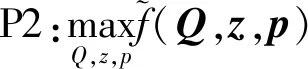
(9)

s.t.(7a)～(7f) 。

可以看出，由于存在对数函数的减法，因此目标函数在自变量Q、z、p上均为非凸函数。求解此类多变量非凸优化问题通常采用连续凸逼近法，即将问题分解为子问题后用循环迭代求解，并在每次循环中用凸函数对非凸函数进行近似。SCA方法能够收敛于原非凸优化问题的某个不动点处[13]，因此将优化问题P2分解为水平轨迹控制、高度控制、功率控制3个子问题，采用SCA方法求近似解。

2 三维航迹控制与功率分配

本文采用循环迭代法求解P2。首先在确定高度、功率的情况下求解水平航迹子问题，再在给定水平航迹、功率的情况下求解高度控制子问题，最后在给定三维航迹的情况下求解功率控制子问题。迭代过程持续直到算法收敛。

2.1 水平航迹子问题

在给定各时隙高度、功率的情况下，向量z、p均为定值。引入松弛变量φ,γ∈N，将水平航迹优化子问题写为

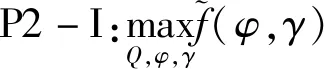
(10a)

s.t.(7a),(7c)，

φ[n]≥‖q[n]‖2,n=1,2,…,N，

(10b)

γ[n]≤‖q[n]-qe[n]‖2,n=1,2,…,N。

(10c)

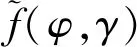
采用SCA方法，在第t次迭代求解非凸问题P2-I时，将式(11)中的非凸函数项用一阶泰勒展开项近似。令第t-1 次迭代求出的最优解为(Q(t-1),φ(t-1),γ(t-1))，作为函数取值点展开一阶泰勒级数，根据对数函数的凹函数性质，有

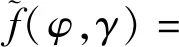
lb(φ[n]+z[n]2)-

lb(σ2(γ[n]+(z[n]-ze[n])2)+

p[n]β0)+lb(γ[n]+(z[n]-ze[n])2))，

(11)

lb(φ[n]+z[n]2)≤lb(φ(t-1)[n]+z[n]2)+

(12)

lb(σ2(γ[n]+(z[n]-ze[n])2)+p[n]β0)≤

lb(σ2(γ(t-1)[n]+(z[n]-ze[n])2)+p[n]β0)+

(13)

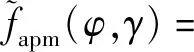
lb(σ2(γ(t-1)[n]+(z[n]-ze[n])2)+p[n]β0)-

lb(γ[n]+(z[n]-ze[n])2))。

(14)

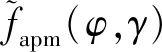
γ[n]≤‖q(t-1)[n]-qe[n]‖2+

2(q(t-1)[n]-qe[n])T(q[n]-qe(t-1)[n])，

(15)

则优化问题P2-I改写为

(16)

s.t.(7b),(7d),(10b),(15)。

此时优化问题P2-II已是标准的凸优化问题，可用标准优化工具如CVX等直接求解，得到的解作为第t次迭代的输出(Q(t),φ(t),γ(t))。

另外，第1次迭代时为保证泰勒级数展开点位于可行域内，可求解以下可行性问题：

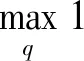
(17)

s.t.(7b),(7d)。

求得符合约束条件的可行解作为Q(0)并按式(10b)、(10c)中的等式约束得到φ(0)、γ(0)，从而得到此时的一阶泰勒级数展开式的函数取值点。

可以看出，求解优化问题P2-II得到的函数最优值是原问题P2-I的下界。

2.2 垂直高度控制子问题

在第t次迭代中求解高度控制子问题时，Q、p是常量。采用SCA方法，和2.1节相似，定义松弛变量θ,η∈N，引入松弛变量约束条件式(18)和式(19)，并将代入松弛变量的目标函数中的非凸函数项做一阶泰勒级数展开，得到的近似函数如式(20)所示。

θ[n]≥z[n]2，

(18)

η[n]≤(z[n]-ze[n])2，

(19)

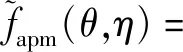
p[n]β0)-lb(θ(t-1)[n]+‖q[n]‖2)-

lb(σ2(η(t-1)[n]+‖q[n]-qe[n]‖2)+p[n]β0)-

lb(η[n]+‖q[n]-qe[n]‖2))。

(20)

则得到经过凸优化近似的高度控制子问题：

(21a)

s.t.(7d),(7f)，

θ[n]≥z[n]2,n=1,2,…,N，

(21b)

η[n]≤(z(t-1)[n]-ze[n])2+

2(z(t-1)[n]-ze[n])(z[n]-z(t-1)[n])。

(21c)

此时优化问题P2-III已经是标准的凸优化问题，可以直接求解。

2.3 功率分配子问题

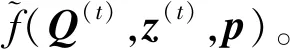
‖q[n]‖2+z[n]2≤‖q[n]-qe[n]‖2+

(z[n]-ze[n])2。

(22)

定理1 给定飞行轨迹Q、z,令p*为优化问题P2的功率变量最优解，则

(23)

由定理1可知，通过将无人机和用户距离和无人机与恶意无人机窃听者之间的距离进行比较，即可唯一确定最优发射功率。当无人机更靠近恶意无人机窃听者时，停止数据传输，否则以最大功率传输数据。

2.4 航迹控制与功率分配联合优化算法

下面给出航迹控制与功率分配联合优化算法运行步骤：

Step1 求解可行性问题(17)得到水平轨迹初始值Q(0)，取任一符合约束条件(7d)、(7f)的序列作为z(0)，令p(0)[n]=pmax,∀n，给定收敛判断阈值ε。

Step2 迭代求解优化问题P2。在第t次迭代中，依次求解：

(1)给定第t-1次迭代的最优解(Q(t-1),z(t-1),p(t-1))，使用CVX工具求解水平航迹优化子问题P2-II，得到水平航迹最优解Q(t)；

(2)根据Q(t)、z(t-1)、p(t-1)的取值，使用CVX工具求解高度控制子问题P2-III，得到高度控制最优解z(t);

(3)根据Q(t)、z(t)的取值，按定理1计算最佳功率p(t)。

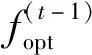
Step4 输出最优解Q*、z*、p*。

2.5 算法复杂度分析

由于联合优化算法在每次迭代中求解子问题P2-II、P2-III，而这两个子问题均是标准凸优化问题，引入了松弛变量，其约束条件分别为3N、4N个线性约束条件，因此求解飞行轨迹和高度控制子问题所需的计算复杂度均分别为Ο((3N)3.5)和Ο((4N)3.5)[8]。令Niter表示SCA方法达到收敛所需的迭代次数，则算法整体复杂度为Ο(((3N)3.5+(4N)3.5)Niter)。

3 仿真实验

本节使用Matlab进行数值仿真来验证方案的有效性。仿真实验参数设置如下：无人机起始位置s0=(-200 m,-100 m,200 m),结束位置sN=(200 m,200 m,200 m)，飞行高度zmax=200 m,zmin=50 m；时隙宽度Ts=1 s；参考部分商用多旋翼无人机的参数，设定飞行速度限制Vd=20 m/s,Vh=6 m/s，最大发射功率pmax=30 dBm；信道参考增益β0=-30 dB，噪声功率σ2=-80 dBm[8]；恶意无人机在x-y平面上以半径r=150 m沿逆时针方向以10 m/s围绕用户飞行；算法收敛阈值ε=0.001。

图2给出了在窃听者是恶意无人机和窃听者是地面攻击者这两种情况下无人机的三维飞行轨迹。图2(a)给出了窃听者为恶意无人机时在不同飞行周期下合法无人机的最优飞行轨迹，恶意无人机以(zmin+zmax)/2的固定高度飞行。可以看出，在各个不同飞行周期下，无人机均首先下降至最低高度以靠近用户。到达最低高度平面后，无人机调整自身的位置以拉开和恶意无人机的距离，并尽量延长在最低高度平面的停留时间，直到在临近周期结束时提升飞行高度以到达结束位置。图2(b)给出了窃听者为地面攻击者时在不同飞行周期下无人机的最优飞行轨迹，地面窃听者坐标为(150 m,0 m,0 m)。可以看到此时无人机下降到高度最低平面后，由于窃听者位置固定，无人机会前往一个固定点处停留，直到临近飞行周期结束再前往结束位置。

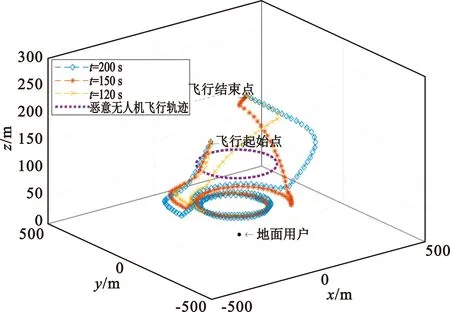
(a)恶意无人机窃听者

图3给出了不同飞行周期下无人机飞行速度和功率变化情况。图3(a)给出了无人机水平方向和垂直方向的瞬时飞行速度，可以看到，在飞行周期开始，无人机以垂直方向和水平方向的最大速度飞行，以尽快调整飞行高度和平面位置以靠近地面用户。当无人机在最低高度调整位置时，由于恶意无人机飞行速率较低(10 m/s)导致位置变化受限，因此无人机的水平飞行速率也有所降低。在飞行周期后段无人机在水平方向逐渐加速至最大速度以靠近结束位置，并在上升阶段将垂直速度提升至最大。图3(b)给出了不同飞行周期下无人机功率的变化情况。在大部分飞行周期内，无人机通过调整自身位置以更接近用户，此时发射功率保持最大值，而在末段飞往结束位置时越来越远离用户，此时发射功率降为0。

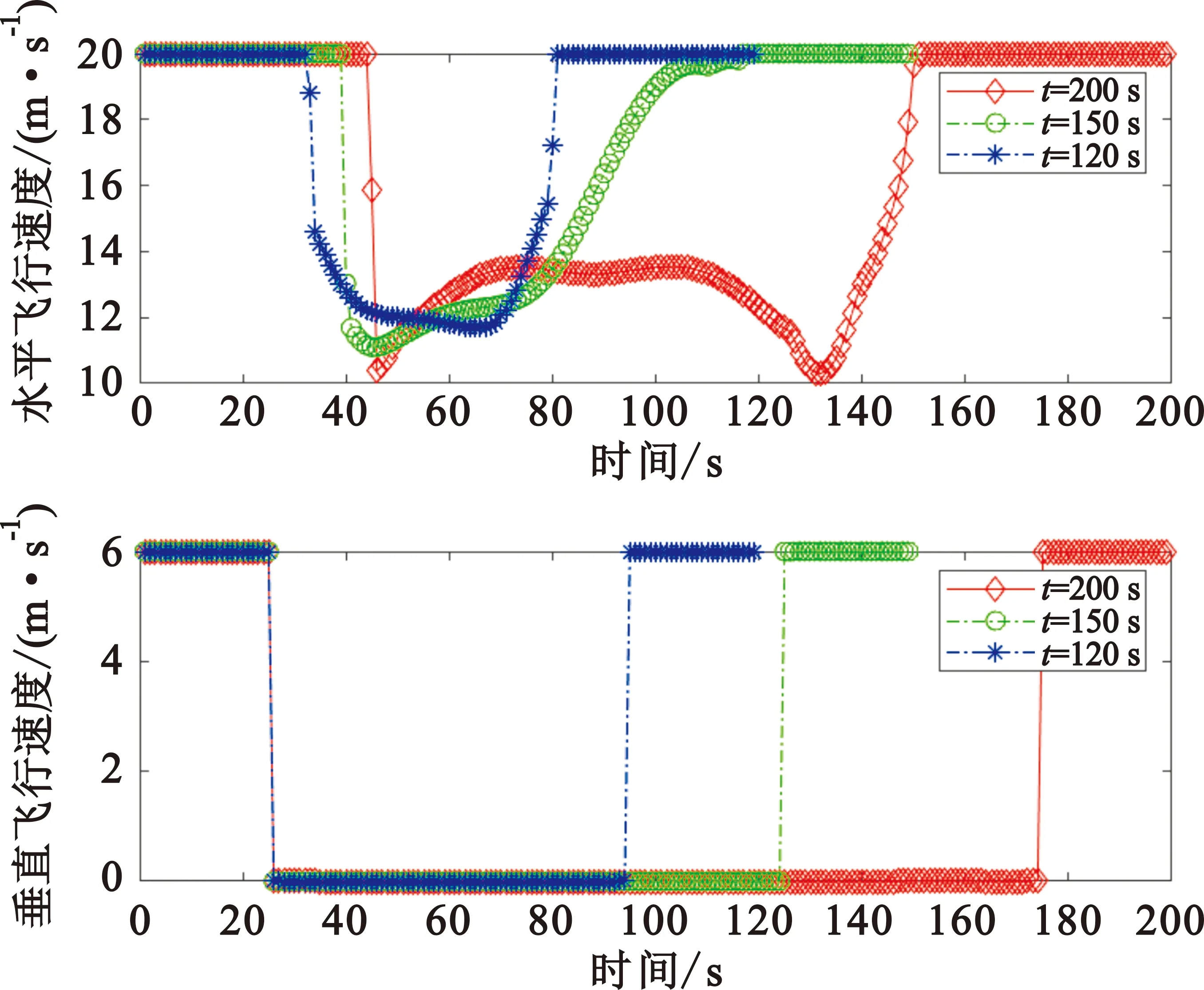
(a)无人机瞬时垂直速率与水平速率

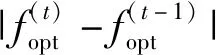
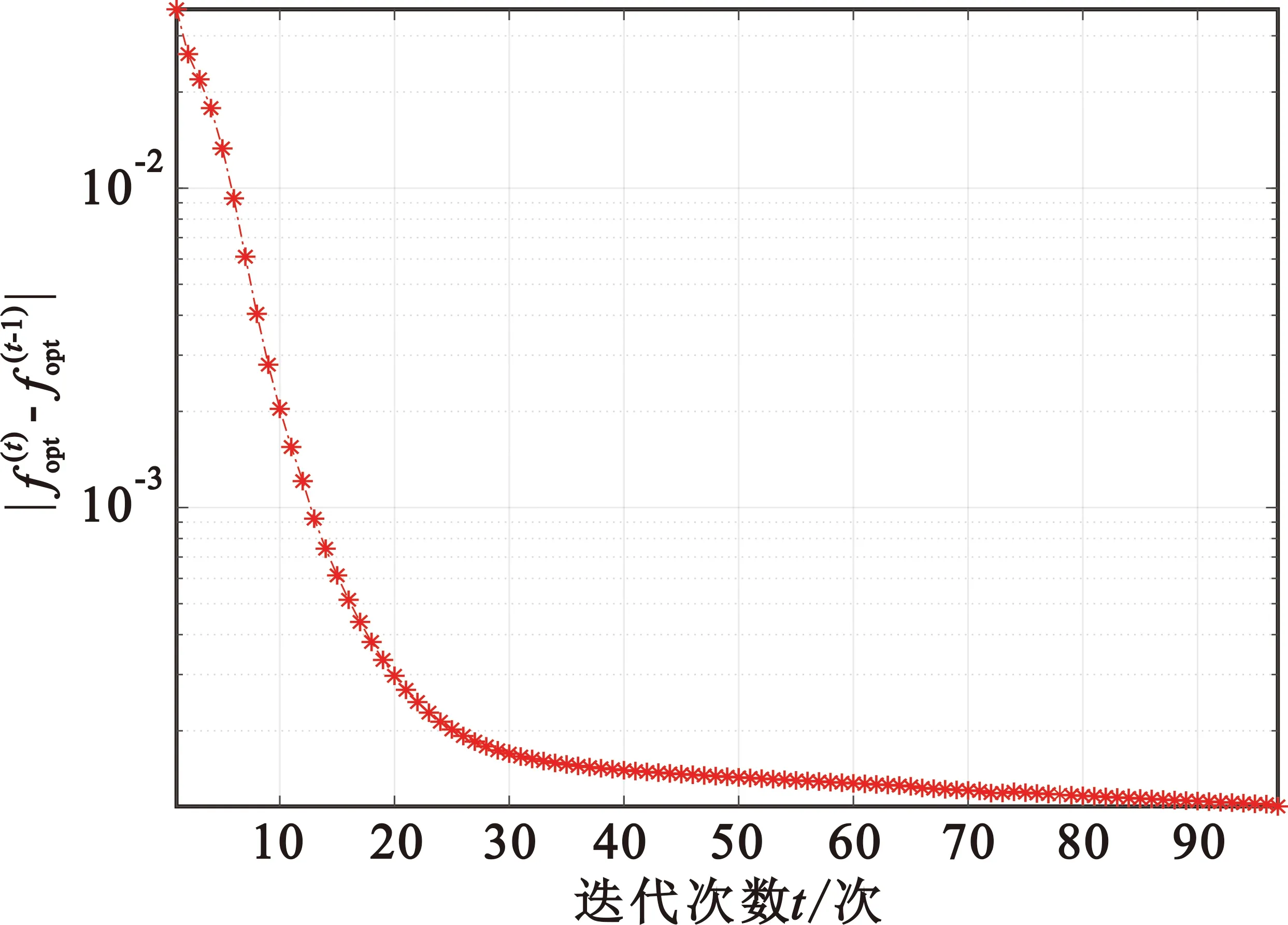
图4 飞行周期T=200 s时相邻两次迭代的函数优化值差值随迭代次数的变化

图5给出了用户平均安全通信速率随不同飞行周期的变化，可以看到，随着飞行周期的增加，平均安全通信速率呈现波动上升的趋势。这是因为无人机在下降和上升阶段中无人机高度较高，离用户位置较远，因此这两个阶段的安全通信速率较低。而受限于垂直方向的速度限制，下降和上升阶段需持续一段时间，飞行周期越短，这两个阶段的时间占比越高，平均安全通信速率就要低一些。随着飞行周期拉长，上升和下降阶段的时间占比变小，带来的影响就降低，而无人机位于最低飞行高度的时间占比大，并且通过水平方向的位移尽量拉大和恶意无人机窃听者的距离，因此具有较高的安全通信速率。与仅采用二维路径规划和功率控制的联合优化方案对比，该对比方案中设定无人机和恶意无人机窃听者飞行在同一高度(zmin+zmax)/2，可以看到三维路径规划和功率控制的联合优化在用户平均安全通信速率上有30%以上的提升。这是因为通过高度的控制，无人机可以更加接近地面用户和更加远离恶意无人机，从而提升了安全通信速率。

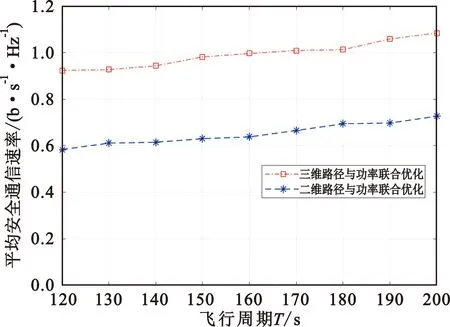
图5 用户平均安全通信速率随飞行周期长度的变化

4 结束语

本文研究了在面临恶意无人机的窃听攻击时无人机通信系统中的无人机最佳三维飞行轨迹和功率分配方案，提出了通过求解带约束的用户平均安全通信速率最大化问题，并将该优化问题分解为3个子问题采用联合优化方式求解。采用连续凸优化逼近方法求得了该优化问题的近似解，并得到了最优功率分配子问题的显示解。仿真实验表明，本文方案能有效实现无人机对地面用户的安全数据传输，并且和二维飞行轨迹控制方案相比，在用户平均安全通信速率上有超过30%的性能提升。

下一步将针对更加复杂的信道模型、信道状态信息和恶意无人机飞行轨迹的不确定性对无人机三维飞行轨迹与功率控制带来的影响展开研究。