GEO SAR照射的机载前视接收双基SAR系统二维分辨能力分析*
张滈铧,左伟华,刘 波
(中国空间技术研究院西安分院,西安710199)
0 引 言
星/机双基合成孔径雷达(Synthetic Aperture Radar,SAR),即将发射机安装在卫星上,并利用机载的接收机共同构成的合成孔径观测系统。而利用高轨卫星SAR作为发射机,本身具有广域覆盖等特点,更是为地球同步轨道(Geostationary Earth Orbit,GEO)星/机双基SAR系统提供了构型灵活多样、可重访时间短、观测持续时间久等优点[1-4]。接收平台只保留无源接收系统,并辅以相应的同步系统即可实现对地成像,可大幅减小接收平台的系统功耗、成本和体积,并进一步降低组成多基SAR系统时多接收平台的成本,为进一步的三维成像、多基线干涉等领域的广泛应用提供了可能。
星/机双基SAR作为新型的遥感技术不仅可以作为重点区域的长期监测,同时星/机双基的构型可以克服单机SAR不具备前视能力的缺陷,为接收机提供飞行方向(或后向)的成像能力,因此可以作为无人航空的导航系统。梯度法[5]通过解析的方法,直观体现出成像几何,即发射和接收机的位置、速度对成像分辨率的影响。Moccia等人[6]最早基于梯度法分析了低轨星/机、中轨星/机、低轨双基等不同双基构型系统的二维分辨率,但并没有针对GEO SAR和机载SAR的分析。李谨成等[7]用梯度法分析了GEO-UAV空天双机SAR在UAV SAR工作在正侧视模式下的二维分辨率。综上,对GEO星/机双基前视SAR的二维分辨率分析有其必要性和现实应用意义。
本文首先分析了GEO星/机双基SAR的应用模型,进一步分析了单位分辨单元分别对应的时延变化率和多普勒变化率的梯度,得到星/机双基前视SAR的二维分辨率;分析了GEO星/机双基前视SAR构型对二维分辨率及其夹角的影响,并给出了构型设计的基本准则;最后通过对GEO处于不同轨道位置时,双基前视SAR系统对点目标进行成像仿真验证了分辨率分析方法的准确性。
1 GEO星/机双基SAR应用模型
假设接收机为机载SAR位于[0,-4,10]km,发射机为GEO SAR。理想条件下,发射机位于坐标系X轴正上方:[25 000,0,36 000]km。发射机入射角为45°,接收机入射角为55°。星/机双基SAR系统对应成像区域的等距离线与等多普勒线分布情况如图1所示,其中,蓝色为等距离线,红色为等多普勒线。
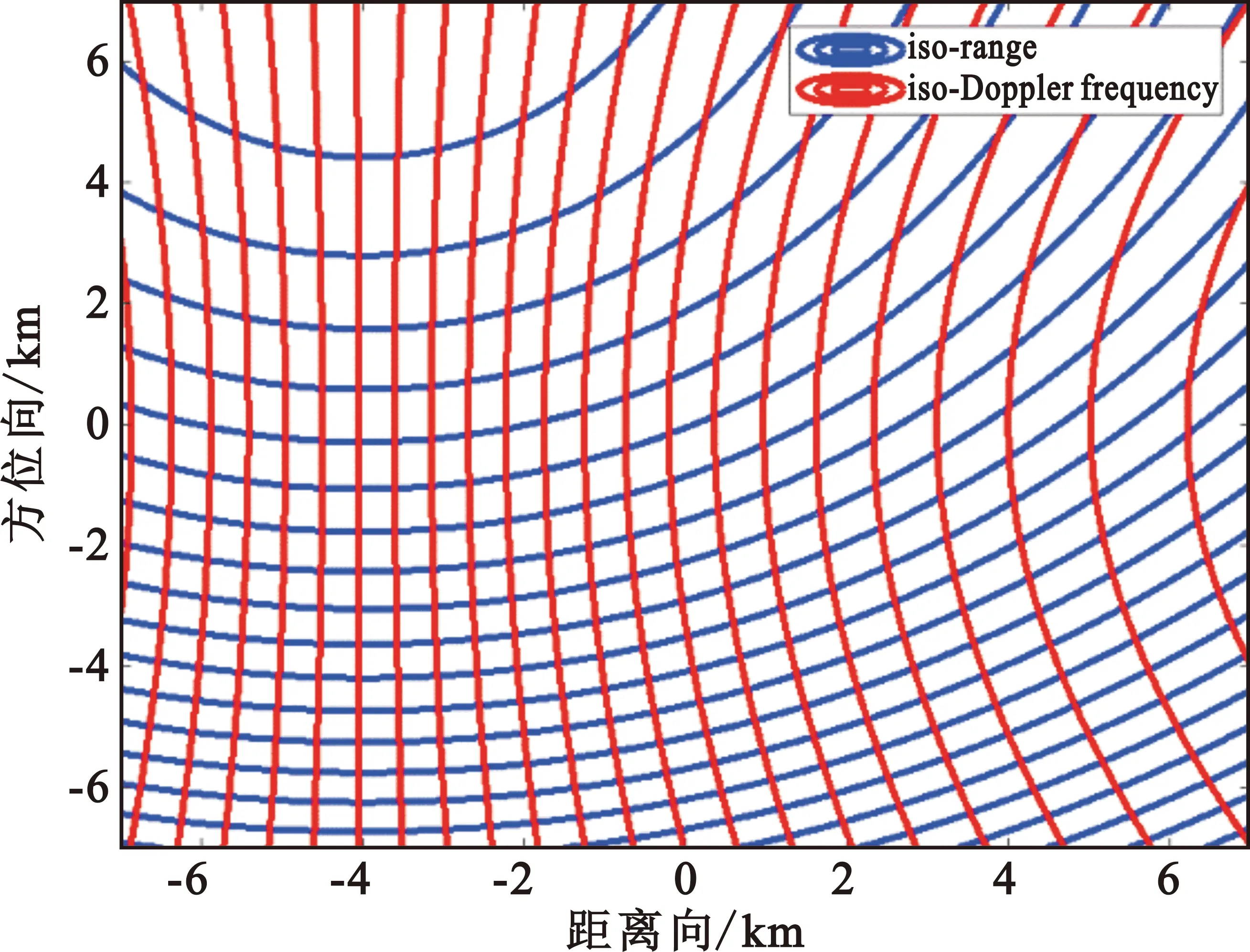
(a)接收机位于[0,-4,10]km
可以看出,在适当构型下,星/机双基SAR系统的等距离线和等多普勒线可以构成完整的二维距离分辨单元,但在同一场景内,随成像位置二维分辨能力(即二维单元形状和大小)并不相同。图1(b)给出了相同条件下,仅改变接收机位置至[14,4,10]km时,等距离线和等多普勒线的分布情况。可以看出,通过更改不同的构型,可以有效调节星/机双基SAR的二维分辨能力。同时从等值线分布可知,机载前视、侧视、后视均可实现等值线二维准正交,具备多视向回波获取能力。
2 分辨率分析
空间分辨率是衡量SAR系统成像性能最重要的指标之一,它表征了SAR系统对场景中相邻目标的分辨能力。距离向和方位向分辨率共同构成SAR系统的空间分辨率,其大小和特性由系统构型、雷达信号参数和工作模式等决定。对于传统单基SAR,距离向指与雷达视线一致的方向,方位向指接收雷达平台沿航迹形成合成孔径的方向[8]。
双基SAR系统包含两个平台的位置信息,运动方向和两个雷达视线方向,上述定义方式不再适用,因此需要寻求SAR方位向和距离向定义的本质。无论单基还是双基,SAR的距离向分辨能力是利用系统对不同点目标的时间延迟的差异来表征区分目标的分辨能力,距离向分辨率可以被定义为单位分辨单元对应的时延变化,即[6]
(1)
式中:rg为以长度表示的距离向的坐标;τ表示快时间。另一方面,从本质上SAR的方位向分辨率,是利用不同点目标的多普勒频率差异来表征区分沿平台航迹方向上相距很近两点的分辨能力。因此,方位向分辨率可以被定义为单位多普勒分辨单元对应的多普勒频率变化,即[6]
(2)
式中:ra为以长度表示的方位向坐标;fD为多普勒频率。
梯度法基于SAR系统是一种相干线性调频雷达的思想,因此可以测算出时延变化和多普勒频率变化的差异,而系统的成像性能就取决于将不同地面检测区域转化为这种变化差异的能力。因此,SAR的方位向和距离向可以被定义为多普勒频率和时间延迟变化最大的方向,单基SAR二维分辨率的定义是式(1)和式(2)的一种简单形式,则SAR系统二维分辨率的计算等价于对多普勒频率和时间延迟最大变化率及其所在方向的求解。
GEO星/机双基地SAR 在地面场景坐标系下的几何结构如图2所示。
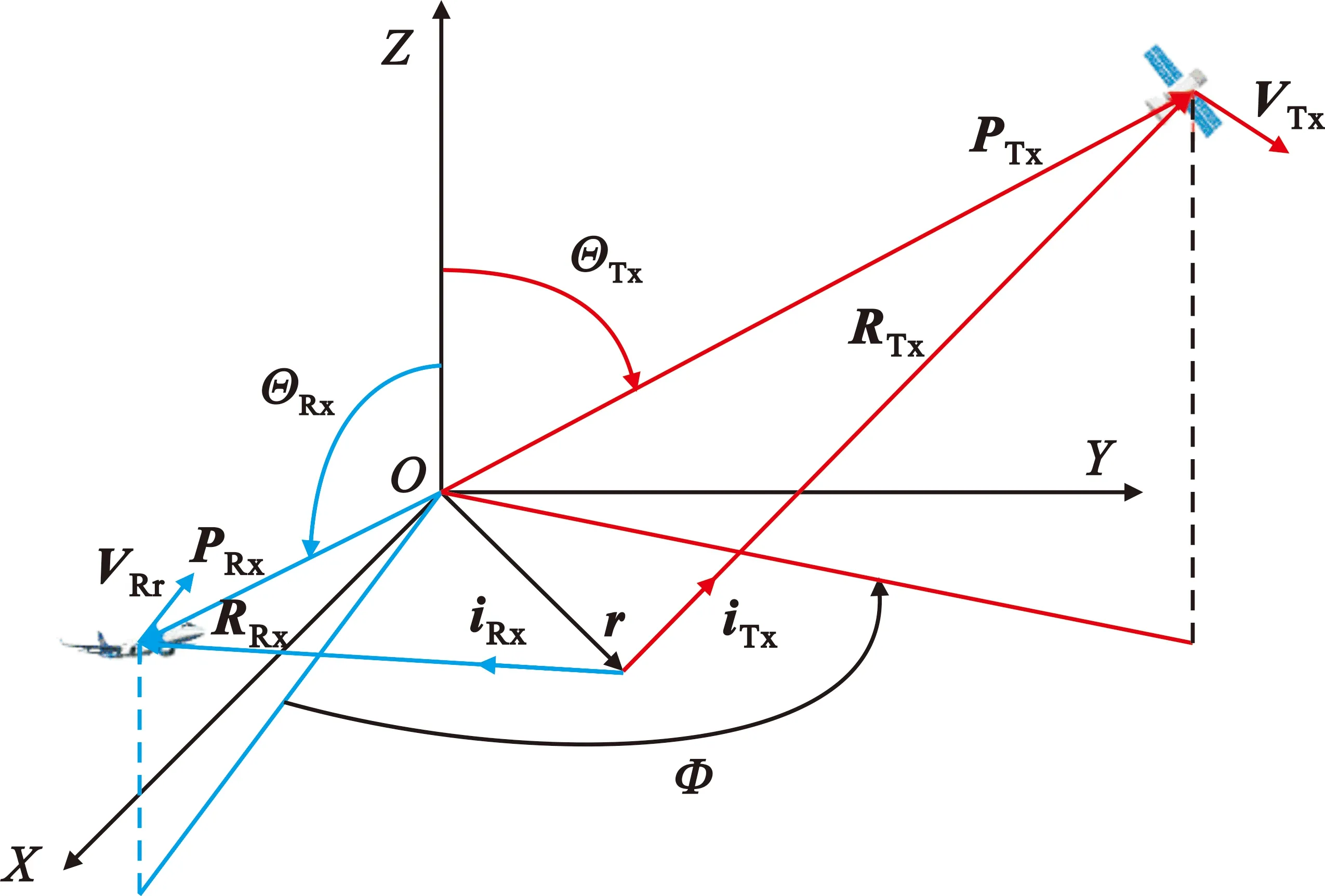
图2 GEO星/机双基地SAR 在地面场景坐标系下的几何结构
假设地球表面是平坦的,并且在整个成像时间内雷达发射机速度VTx与雷达接收机速度VRx为常量。图中,RTx与RRx分别表示发射机与接收机相对点目标的相对位置向量,iTx与iRx分别为沿RTx与RRx方向的单位向量,PTx与PRx分别是发射平台与接收平台的位置向量,r为点目标的位置向量,Φ为双基地角的地面投影角(此后简称为双基角),ΘTx与ΘRx分别表示位置向量PTx和位置向量PRx同Z轴的夹角。
根据图中所示的几何结构,可以得到GEO星/机双基地SAR回波信号的时间延迟为
(3)
式中:τ表示距离向时间;c表示光速。则回波信号的时延等值线可以表示成
t(τ,r)=const。
(4)
由式(3)可以计算出时延t的梯度为

(5)
根据梯度的定义,梯度表示由于r的变化而导致的时间τ变化的度量:

(6)
式中:dr为r的微分;t的梯度表示时延最大变化的方向,也是距离分辨率变化的最小方向。可以看出,时延梯度的方向是沿着收发机平分向量,也即最佳距离分辨率的方向。因此,当系统带宽为B时,可以计算出系统的距离分辨率大小为
(7)

(8)

(9)
(10)
根据图2中所示的双基地几何结构,点目标的双基地距离历程可以表示为
RTx(ta,r)+RRx(ta,r)=(PTx(ta=0)-r)+VTxta+
(PRx(ta=0)-r)+VRxta,
(11)
则回波的相位历程为
(12)
式中:λ表示雷达信号的波长。点目标的多普勒频率历程可以通过对相位历程fD(ta,r)进行求导得到:
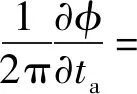
(13)
由于静止目标的位置向量r在整个成像时间内为一常量,因此,其相位梯度为

(14)
则其多普勒频率的梯度为

(15)

(16)
式中:T为合成孔径时间。
由于双基SAR成像的基础就是通过对时延和多普勒的测量产生图像像素实现二维分辨,由公式(8)和(16)中的二维分辨矢量可以定义星/机双基SAR的分辨单元。星/机双基SAR的二维分辨单元为平行四边形,其二维高度分别为drg与dra,其夹角由二维分辨矢量的指向决定并且可以表示为
Ω=arccos(itg·ifg)。
(17)
二维分辨单元的面积为
(18)
由公式(18)可知,星/机双基SAR 的二维分辨单元的大小不仅与其二维分辨矢量的绝对大小(即二维分辨率)有关,还与两者之间的夹角有关。当两者相互正交(Ω=90°)时,在相同的二维分辨率下能够实现最优二维分辨;与当两者的指向互相平行(Ω=0°或Ω=180°)时,星/机双基 SAR 的等距线和方位向等多普勒线相互平行,此时的星/机双基SAR 不具备二维分辨能力。当Ω角度接近0°和180°时,二维分辨能力较差。
3 二维分辨能力与构型的关系
3.1 距离分辨率
根据公式(18)可知,GEO星/机双基前视SAR的距离分辨率只与收、发机入射角和双基角有关。由于入射角的取值范围均是[0°,90°],由公式(9)可知,当cosΦ=1(双基角为0°)时取得最佳距离分辨率,此时对应双基同侧观测模型;当cosΦ=0(双基角为180°)时取得最差距离分辨率,此时对应双基对侧观测模型,即
可见,双基角为180°,收发机入射角相同时,收发双基角的平分线垂直于地面,即回波时延的梯度方向垂直于地面,在地面投影分量为零,理论上此时GEO星/机双基SAR没有地距分辨能力。
图3给出了发射信号带宽250 MHz,发射入射角为45°,不同的接收机入射角下GEO星/机双基前视SAR随双基角的变化关系,可以看出接收入射角和发射入射角差异越大,距离分辨率的最大值的情况就越差。图中黑色直线表示GEO单基SAR的距离分辨率。需要注意的是,无论是双基构型中接收机前视或侧视,距离分辨率特性分析和变化是一样的。
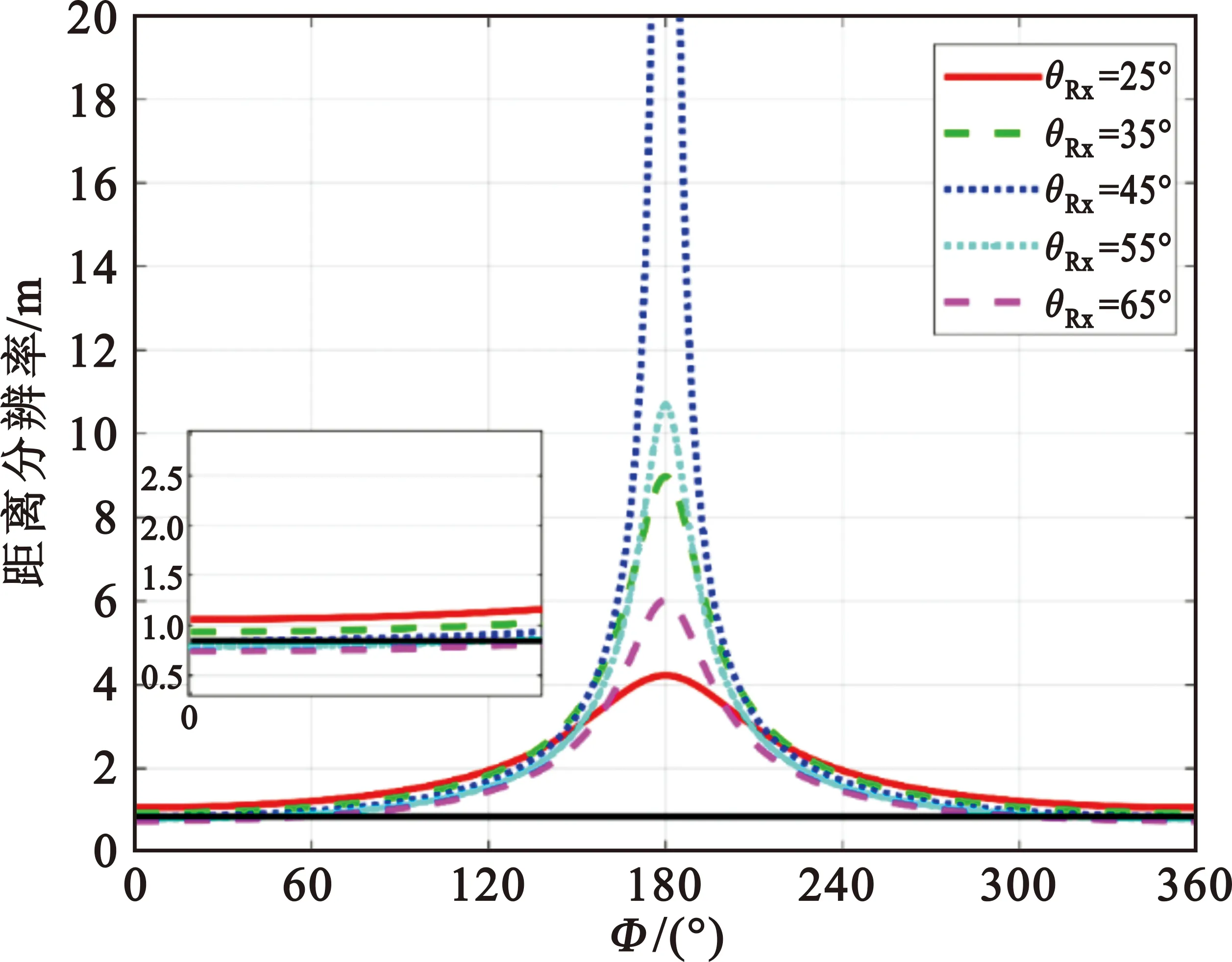
图3 GEO星/机双基前视SAR距离分辨率随双基角变化情况
3.2 方位向分辨率
通过公式(13)和(14)可以看出,方位分辨率不仅与收发机的位置有关,还与收发机的速度矢量及收发斜距有关。假设理想条件下,发射机位于GEO卫星上,轨道高度约为35 800 km,入射角为45°,接收机高度2 km,接收入射角为55°情况下,星/机双基SAR的方位向多普勒分辨率随双基角Φ和双基速度夹角Ψ的变化情况如图4所示。

(a)多普勒分辨率随Φ和Ψ的变化关系
如图4(a)所示,方位向多普勒分辨率可以看作Φ和Ψ的函数,并随之变化。但即使在最差的情况即Ψ≅180°,此时GEO卫星发射机和机载接收机的运动速度方向矢量相反,且Φ≅90°或Φ≅270°时多普勒分辨率仍然小于1.4。这显然得益于高轨卫星的广域照射及较低的波束移动速度,同时GEO卫星作为发射机时在双基构型下对多普勒的贡献率较低。
图4(b)给出了当速度夹角Ψ=65°时,多普勒分辨率随双基角Φ和入射角的变化情况。可以看出同一双基角下,随入射角增加多普勒分辨率变差,符合单机前视多普勒分辨率的变化规律。同一入射角下,多普勒分辨率随双基角的变化很小。
综上,根据上述仿真参数,图5给出了在对应构型下,GEO星/机双基前视SAR随双基角Φ和入射角ΘRx变化,距离分辨率和方位向多普勒分辨率的分布等高线分布情况。红色等高线为距离分辨率,蓝色等高线为方位分辨率,距离分辨率在双基角为180°附近最差。
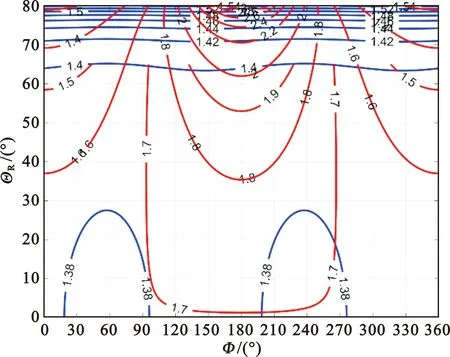
图5 GEO星/机前视SAR系统的二维分辨率等高线分布(发射机入射角为45°)
3.3 二维分辨率夹角
GEO星/机双基前视SAR系统中,工作在前视模式下的机载SAR作为接收机,即速度矢量方向与位置矢量方向在地面投影相反,很大程度上影响了二维分辨夹角的变化情况。图6给出了GEO星/机双基前视SAR二维分辨率夹角Ω随双基角Φ、速度矢量夹角Ψ和入射角ΘRx的变化情况。
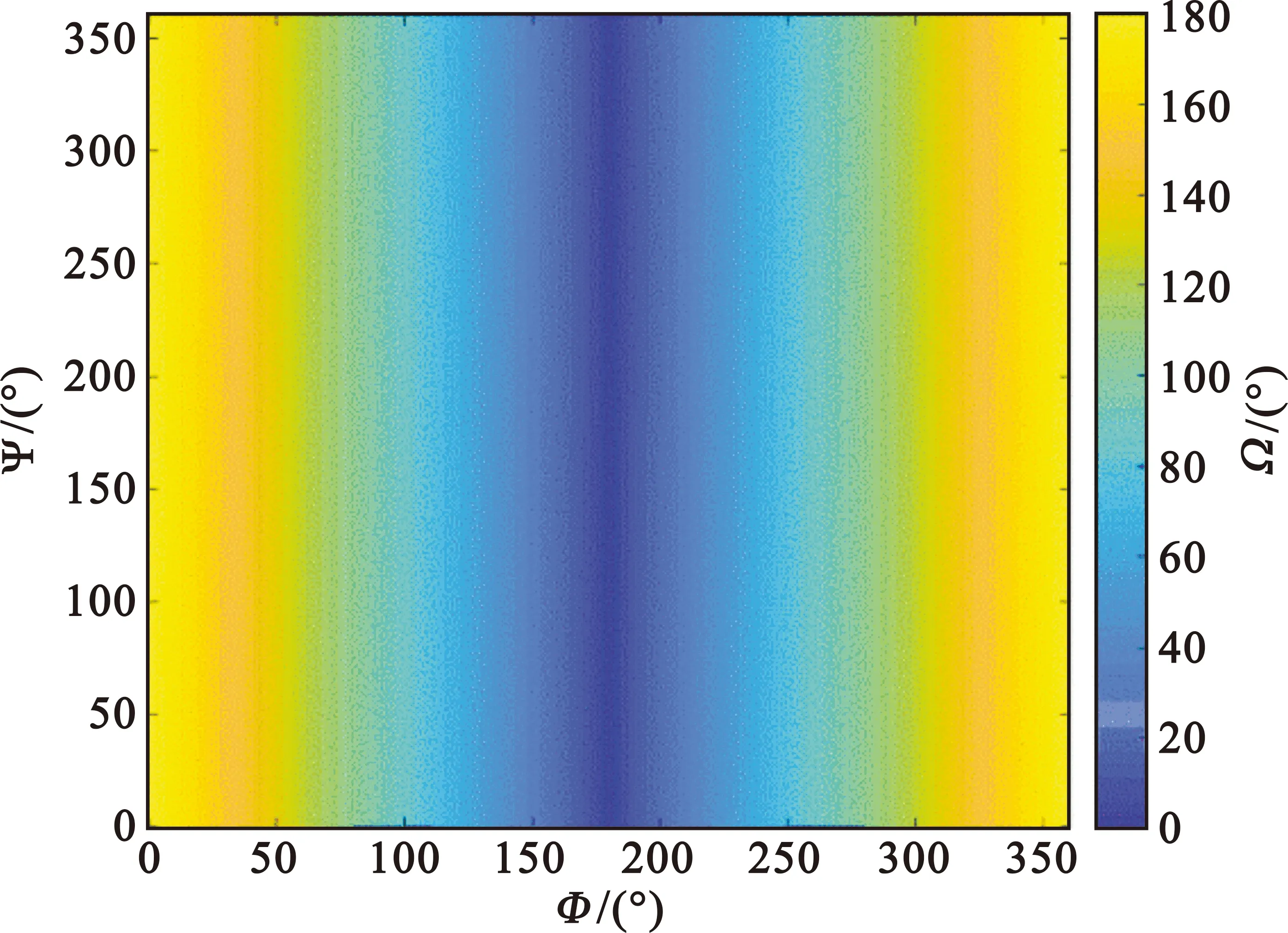
(a)二维分辨率夹角随Φ和Ψ的变化关系
不同于双基侧视SAR系统,GEO星/机双基前视SAR的二维分辨率夹角Ω特性随双基角Φ的影响显著,如图6所示其变化范围较大,且在前视构型下有明显的产生模糊的构型(如Ω接近0°或180°)。速度矢量夹角Ψ对二维分辨率夹角Ω在双基前视构型下没有影响,这同一般的双基侧视构型有很大的差别。这本质上是由产生模糊的前视SAR构型引起的,而作为单机的前视SAR会在左右产生模糊区域,而作为前视接收机置于双基构型中,当构型中的发射机可以实现旋转等距线和等多普勒线时得以消除模糊。
图6(b)给出了在双基角为70°情况下,二维分辨率夹角随入射角ΘRx和速度夹角Ψ变化,与图6(a)特性对应一致,Ω大概在115°上下,同一入射角下不同速度夹角对二维分辨率夹角影响不大,但不同入射角下二维分辨率的夹角有明显的变化,在一些可成像区域的边缘需要注意接收机入射角的设计。
3.4 构型设计关系
通常在GEO星/机双基前视SAR系统中,系统观测的场景以及发射机的位置、速度矢量都是已知的,接收机的速度矢量与位置矢量的投影相反实现前视。构型设计就是对双基角Φ和速度夹角Ψ以及接收机入射角ΘRx的设计。为了保证系统具备二维分辨能力,距离分辨率方向应与方位向分辨率方向尽可能正交,即30°≤Ω≤150°。作为前视成像,二维成像单元的面积A应小于4 m2。
为了方便,这里假设接收机位于X轴正向,且前视速度方向指向X轴负方向,以原点为参考点。在上述条件下,图7给出了GEO卫星在星/机双基SAR系统中位置矢量和速度矢量适合成像的示意图。
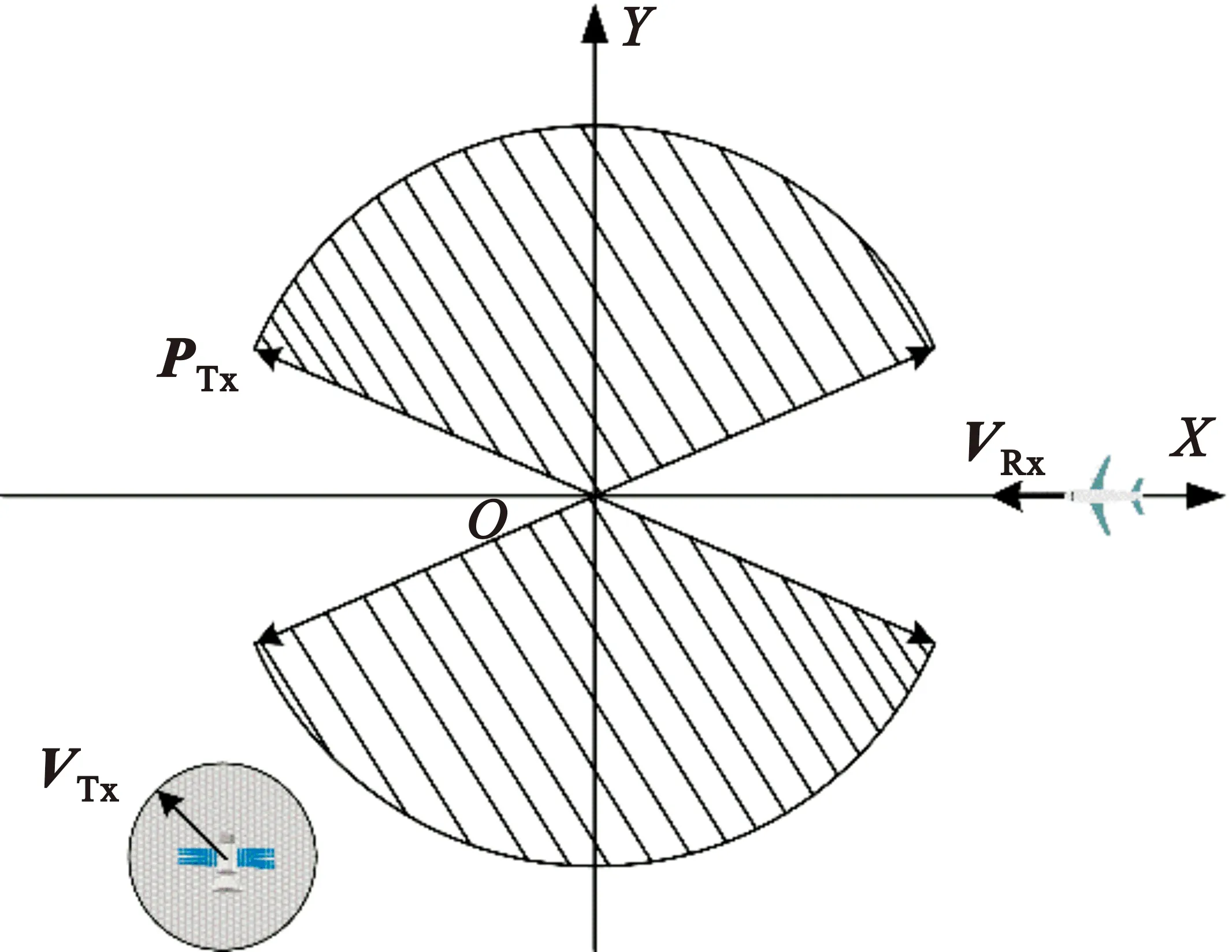
图7 GEO星/机双基前视SAR可成像构型的发射机位置矢量和速度矢量
需要注意的是,当GEO卫星采用0偏心率、低轨道倾角时,由于此时GEO卫星的对地速度及波束速度过小,近似于固定照射,此时多普勒分辨率全部由机载接收机贡献,双基构型设计无法实现距离和方位多普勒的二维分辨。
4 分析验证
为了验证GEO星/机双基前视SAR二维分辨能力的分析方法有效性,选取轨道离心率为0.005,轨道倾角57°,升交点赤经106°,近地点幅角90°的GEO卫星为发射机,其星下点轨迹为“8”字形,下视角为3°,分别计算出卫星在不同时刻下的位置矢量、速度矢量,以方位向零时刻对应的波束中心点为原点建立东北天坐标系(ENU),计算GEO星/机双基前视SAR系统的距离分辨率和方位向分辨率大小,并成像验证。
假设接收机高度2 km,位于ENU坐标系X轴的负半轴(西方向),向原点方向(自西向东)平飞速度恒定,入射角为55°。假设GEO卫星轨道高度3.57×104km,利用上述分析方法得到该构型下GEO卫星处于不同位置矢量和速度矢量的情况下,星/机双基前视SAR的距离分辨率和方位向多普勒分辨率的分布等高线分布情况如图8所示,红色等高线为距离分辨率,蓝色等高线为方位分辨率,距离分辨率在双基角为180°附近最差。
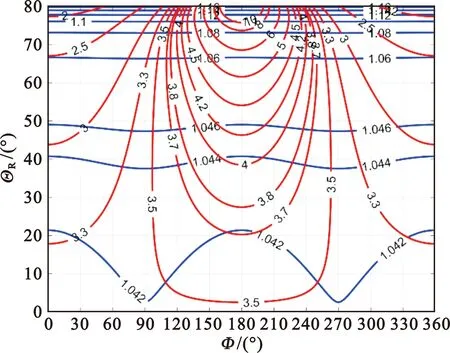
图8 GEO卫星在近地点双基前视SAR的二维分辨率分布(接收机位于参考点正东)
以GEO卫星处于近地点为例进行分析,此时GEO卫星波束的星下点经度为106°,纬度为74.2°。以该点为原点建立本地坐标系(ENU坐标系),计算得到该时刻对应的GEO卫星位置[0,-12 407,33 718]km和速度矢量[1 423.9,0.1,0]m/s,入射角可计算得到20.2°。
利用NLCS(Nolinear Chirp Scaling)算法进行成像验证[9]。图9给出了该构型下的成像结果,其中,图9(a)表示点目标的距离向切片,图9(b)表示点目标的方位向切片,图9(c)表示点目标利用NLCS成像算法得到的成像结果等高线图,图9(d)表示原始的回波信号。
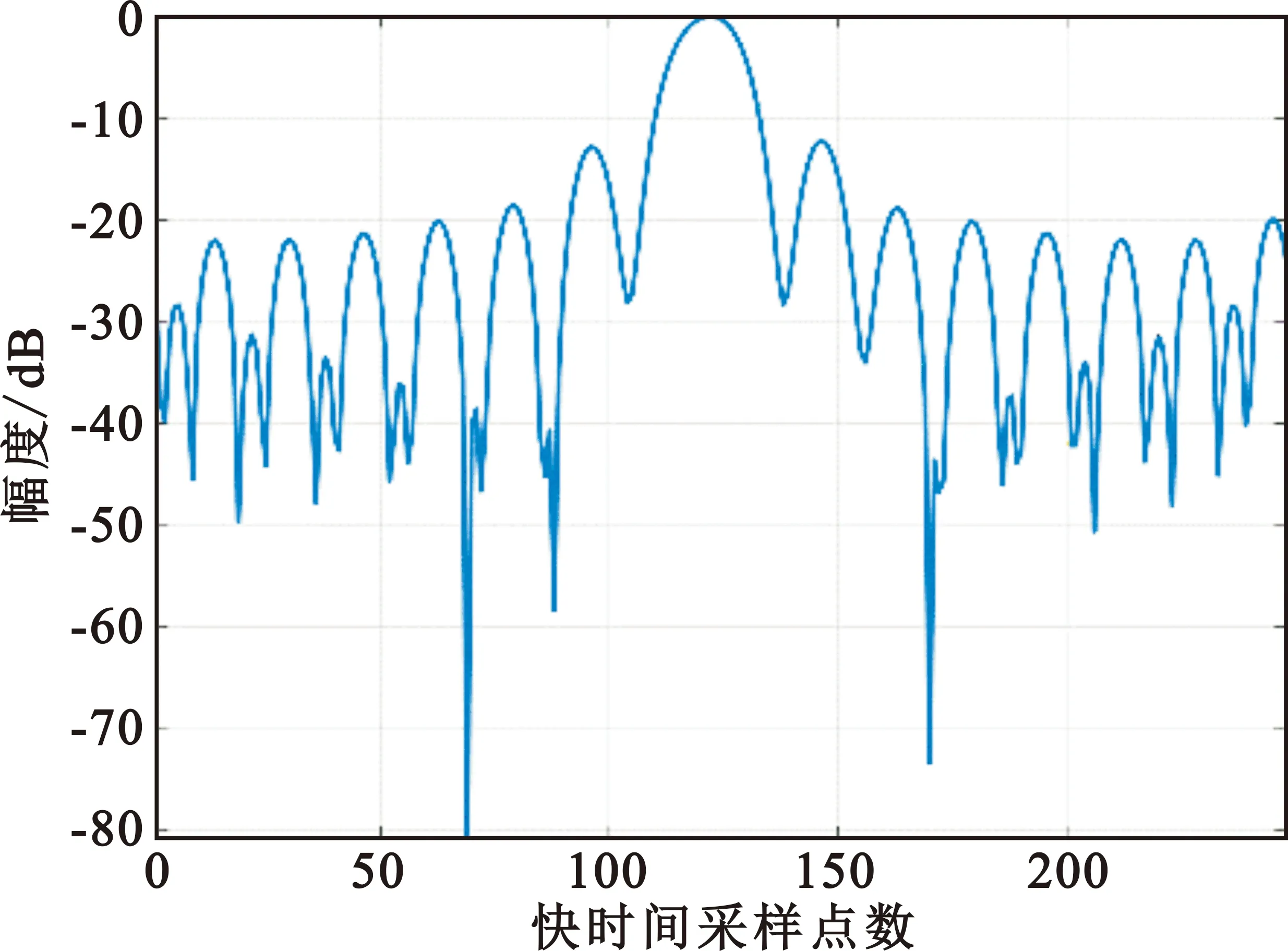
(a)点目标的距离向切片
该构型下通过NLCS算法对原点进行成像,进一步计算得到距离向分辨率约为3.281 m,方位向分辨率约为1.021 m,根据回波原始信号计算出分辨率夹角为79.1°。此时双基角Φ为90°,速度夹角Ψ为0°,接收入射角ΘRx为55°,根据图8可以看出,对应构型下的理论分析的计算值分别为距离分辨率3.43 m,方位分辨率1.05 m,分辨率夹角77°;距离向峰值旁瓣比(Peak Sidelobe Ratio,PSLR)为-12.30 dB,积分旁瓣比(Integral Sidelobe Ratio,ISLR)为-10.35 dB;方位向PSLR为-13.04 dB,ISLR为-10.86 dB。成像计算结果与理论分析得到的分辨率仿真结果基本一致。
当GEO卫星在近地点,仅改变接收机位置位于任意方向,当与X轴正方向夹角160°时,入射角等其他条件不变,前视成像。通过NLCS成像算法成像,得到距离向分辨率为4.173 m,方位向分辨率为1.122 m,分辨率夹角为46.2°,与图8该构型理论分析得到的仿真结果基本一致。
进一步对GEO卫星位于赤道附近和远地点附近分别进行了成像和分辨率分析仿真,此时接收机位于GEO卫星波束中心点正东,自西向东向前视移动。当GEO卫星位于赤道附近的时候,以方位零时刻的波束中心点为原点建立ENU坐标系,发射机的位置矢量为[-11 109,5 729,33 892]km,速度矢量为[-1 349,-2 605.6,0]m/s。接收机此时位于X轴正半轴,向负向恒定速度飞行。根据上述分辨率分析方法,该构型下的理论分析距离向分辨率为3.92 m,方位向分辨率为1.26 m,二维分辨率夹角为125°;距离向PSLR为-12.63 dB,ISLR为-10.15 dB;方位向PSLR为-13.22 dB,ISLR为-10.96 dB。通过NLCS进行成像仿真结果如图10所示,通过成像算法仿真得到的距离向分辨率为3.46 m,方位向分辨率为1.33 m,二维分辨率夹角为130.6°,与该构型理论分析计算的结果基本相符。

(a)点目标的距离向切片
当GEO卫星位于远地点附近的时候,以方位零时刻的波束中心点为原点建立ENU坐标系,发射机的位置矢量为[0,-12 655,34 072]km,速度矢量为[1 376.4,-0.1,0]m/s。接收机此时位于X轴正半轴,向负向恒定速度飞行。根据上述分辨率分析方法,该构型下的理论分析距离向分辨率为3.36 m,方位向分辨率为1.041 m,二维分辨率夹角为80.6°。通过NLCS进行成像仿真,结果如图11所示。
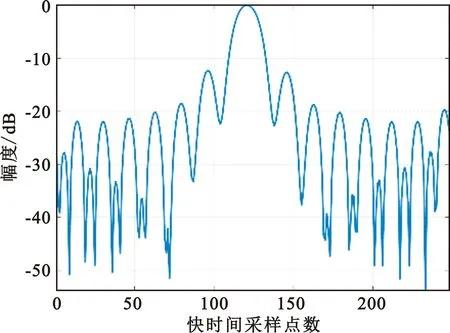
(a)点目标的距离向切片
通过成像算法仿真得到的距离向分辨率为3.516 m,方位向分辨率为1.05 m,二维分辨率夹角为83.2°;距离向PSLR为-12.63 dB,ISLR为-10.15 dB;方位向PSLR为-13.09 dB,ISLR为-10.96 dB,与该构型理论分析计算的结果基本相符。
综上所述,利用梯度法对GEO星/机双基前视SAR系统的分辨率分析方法准确性和可靠性较高。
5 结 论
本文利用梯度法来解析计算得到GEO星/机前视SAR系统的二维分辨率情况。考虑高轨SAR作为发射机,结合了高轨卫星的轨道特点,分析了发射机在不同轨道位置处与对应机载前视接收机组成不同几何构型下SAR系统的成像能力。通过利用回波时延梯度和多普勒频率梯度的计算,可以较准确地计算出二维分辨率大小,对GEO星/机前视SAR的分辨率分析和构型设计具有一定的指导意义。

